2023年中考数学专题——化简求值五大分类训练

完整word版)中考数学化简求值专项训练中考数学化简求值专项训练注意：此类题目的要求是化简之后再代入求值，直接代入求值不得分。

考点包括分式的加减乘除运算（注意去括号，添括号时要变号，分子相减时要看做整体）、因式分解（十字相乘法、完全平方式、平方差公式、提公因式）以及二次根式的简单计算（分母有理化，一定要是最简根式）。

类型一：化简之后直接带值，有两种基本形式：1.含根式，这类带值需要对分母进行有理化，一定要保证最后算出的值是最简根式。

例如，化简并求值：$\frac{m^2-2m+1}{m-1-\frac{1}{m+1}}$，其中$m=3$。

解：先化简分母，得到$\frac{m^2-1}{m^2-1}$，然后将分子分母同时化简，得到$\frac{(m-1)^2}{m}$。

代入$m=3$，得到$\frac{4}{3}$。

2.常规形，不含根式，化简之后直接带值。

例如，化简并求值：$\frac{x^3-6x^2+9x-1}{x^2-3x}$，其中$x=-6$。

解：先化简，得到$\frac{(x-3)^2}{x(x-3)}$。

代入$x=-6$，得到$\frac{1}{6}$。

3.化简并求值：$\frac{11+2x}{x-y}$，其中$x=1$，$y=-2$。

解：先化简，得到$\frac{11+2x}{x-y}=\frac{13}{3}$。

代入$x=1$，$y=-2$，得到$\frac{13}{3}$。

4.化简并求值：$\frac{x^2-2x}{2x-4}+\frac{2}{x+2}$，其中$x=0.5$。

解：先化简，得到$\frac{x(x-2)}{2(x-2)}+\frac{2}{x+2}=\frac{x}{2}+\frac{1}{x+2}$。

代入$x=0.5$，得到$\frac{5}{4}$。

5.化简并求值：$\frac{1-x}{2x}+\frac{2x}{x^2-4x+3}$，其中$x=2$。

解：先化简，得到$\frac{1}{2}-\frac{2x-3}{x-1}\cdot\frac{1}{x-3}=\frac{5}{6}$。

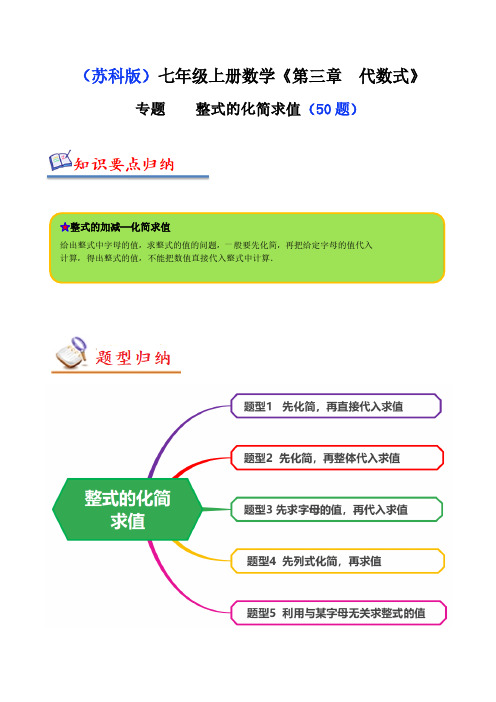
（苏科版）七年级上册数学《第三章代数式》专题整式的化简求值（50题）1．先化简再求值：2x 2y−[x y 2+3(x 2y−13x y 2)]，其中x =12，y ＝2．2．先化简，再求值：4x 2﹣2xy +y 2﹣（x 2﹣xy +y 2），其中x ＝﹣1，y =−12．3．（2022秋•秦淮区期末）先化简，再求值：7a 2b +（﹣4a 2b +5ab 2）﹣（2a 2b ﹣3ab 2），其中a ＝﹣1，b ＝2．4．（2022秋•邹城市校级期末）先化简，再求值：（2x 2﹣2y 2）﹣4（x 2y +xy 2）+4（x 2y 2+y 2），其中x ＝﹣1，y ＝2．5．（2023•青秀区校级开学）先化简，再求值：4x+2（3y2﹣2x）﹣3（2x﹣y2），其中x＝2，y＝﹣2．6．（2022秋•龙沙区期中）先化简，再求值：﹣（3a2﹣4ab）+[a2﹣2（2a+2ab）]，其中a＝﹣2，b＝2022．7．（2022秋•南海区校级期末）先化简，再求值：（2x2﹣2y2）﹣3（x2y2+x2）+3（x2y2+y2），其中x＝﹣1，y＝2．8．（2022秋•梁子湖区期末）先化简，再求值：5x2−[2xy−3(13xy+2)+4x2]，其中x=−2，y=12．9．先化简，再求值：2（ab −32a 2+a ﹣b 2）﹣3（a ﹣a 2+23ab ），其中a ＝5，b ＝﹣2．10．先化简，再求值：2（mn ﹣4m 2﹣1）﹣（3m 2﹣2mn ），其中m ＝1，n ＝﹣2．11．先化简再求值：5xy ﹣（4x 2+2y ）﹣2（52xy +x 2），其中x ＝3，y ＝﹣2．12．（2022秋•绿园区期末）先化简，再求值：12m−(2m−23n 2)+(−32m +13n 2)，其中m =−14，n =−12．13．（2022秋•万秀区月考）先化简，再求值2（a2b+ab）﹣4（a2b﹣ab）﹣4a2b，其中a＝3，b＝﹣2．14．（2022秋•陕州区期中）先化简，再求值3x2y−2(x2y+14x y2)−2(x y2−xy)，其中x=12，y＝﹣2．15．（2022秋•沈北新区期中）化简并求值．（1）2（2x﹣3y）﹣（3x+2y+1），其中x＝2，y＝﹣0.5（2）﹣（3a2﹣4ab）+[a2﹣2（2a+2ab）]，其中a＝﹣2．16．先化简，再求值．若m2+3mn＝﹣5，则代数式5m2﹣[5m2﹣（2m2﹣mn）﹣7mn+7]的值．17．（2022秋•密云区期末）先化简，再求值：（4x2+1）﹣2（x2+3x﹣1），其中x2﹣3x＝5．18．（2022秋•密云区期末）先化简，再求值：（4x2+1）﹣2（x2+3x﹣1），其中x2﹣3x＝5．19．已知x+y＝6，xy＝﹣4，求：（5x+2y﹣3xy）﹣（2x﹣y+2xy）的值．20．（2022秋•范县期中）已知m+4n＝﹣1．求（6mn+7n）+[8m﹣（6mn+7m+3n）]的值．21．（2022秋•荔湾区期末）已知a2+b2＝3，ab＝﹣2，求代数式（7a2+3ab+3b2）﹣2（4a2+3ab+2b2）的值．22．（2022秋•平昌县期末）先化简，再求值．已知代数式2（3x2﹣x+2y﹣xy）﹣3（2x2﹣3x﹣y+xy），其中x+y=67，xy＝﹣2．23．有这样一道题“如果代数式5a+3b的值为﹣4，那么代数式2（a+b）+4（2a+b）的值是多少？”爱动脑筋的吴爱国同学这样来解：原式＝2a+2b+8a+4b＝10a+6b．我们把5a+3b看成一个整体，把式子5a+3b ＝﹣4两边乘以2得10a+6b＝﹣8．整体思想是中学数学解题中的一种重要思想方法，它在多项式的化简与求值中应用极为广泛，仿照上面的解题方法，完成下面问题：【简单应用】（1）已知a2﹣2a＝1，则2a2﹣4a+1＝ ．（2）已知m+n＝2，mn＝﹣4，求2（mn﹣3m）﹣3（2n﹣mn）的值．【拓展提高】（3）已知a2+2ab＝﹣5，ab﹣2b2＝﹣3，求代数式3a2+4ab+4b2的值．24．阅读材料：我们知道，4x﹣2x+x＝（4﹣2+1）x＝3x，类似地，我们把（a+b）看成一个整体，则4（a+b）﹣2（a+b）+（a+b）＝（4﹣2+1）（a+b）＝3（a+b）．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．尝试应用整体思想解决下列问题：（1）把（a﹣b）2看成一个整体，合并3（a﹣b）2﹣6（a﹣b）2+2（a﹣b）2．（2）已知x2﹣2y＝4，求3x2﹣6y﹣21的值；（3）已知a﹣2b＝3，2b﹣c＝﹣5，c﹣d＝10，求（a﹣c）+（2b﹣d）﹣（2b﹣c）的值．25．阅读理解：已知4a−52b＝1，求代数式2（a﹣b）+3（2a﹣b）的值．解：因为4a−52b＝1，所以原式=2a−2b+6a−3b=8a−5b=2(4a−52b)=2×1=2．仿照以上解题方法，完成下面的问题：（1）已知a﹣b＝﹣3，求3（a﹣b）﹣a+b+1的值；（2）已知a2+2ab＝2，ab﹣b2＝1，求2a2+5ab﹣b2的值．26．（2022秋•祁阳县期末）图是湘教版七年级上册数学教材65页的部分内容．明明同学在做作业时采用的方法如下：由题意得3（a2+2a）+2＝3×1+2＝5，所以代数式3（a2+2a）+2的值为5．【方法运用】：（1）若代数x2﹣2x+3的值为5，求代数式3x2﹣6x﹣1的值；（2）当x＝1时，代数式ax3+bx+5的值为8．当x＝﹣1，求代数式ax3+bx﹣6的值；（3）若x2﹣2xy+y2＝20，xy﹣y2＝6，求代数式x2﹣3xy+2y2的值．27．（2022秋•惠东县期中）有这样一道题“如果式子5a+3b的值为﹣4，那么式子2（a+b）+4（2a+b）的值是多少？”爱动脑筋的佳佳同学这样来解：原式＝2a+2b+8a+4b＝10a+6b．我们把5a+3b看成一个整体，则原式＝2（5a+3b）＝2×（﹣4）＝﹣8．整体思想是中学数学解题中的一种重要思想方法，它在多项式的化简与求值中应用极为广泛，仿照佳佳的解题方法，完成下面问题：（1）已知a2﹣2a＝1，则2a2﹣4a+1＝　；（2）已知m+n＝2，mn＝﹣4，求2（mn﹣3m）﹣3（2n﹣mn）的值；（3）已知a2+2ab＝﹣5，ab﹣2b2＝﹣3，求3a2+4ab+4b2的值．28．（2022秋•西安期中）化简求值：−12(5xy−2x2+3y2)+3(−12xy+23x2+y26)，其中x、y满足（x+1）2+|y﹣2|＝0．29．（2022秋•公安县期中）先化简，再求值：4a2b﹣[﹣2ab2﹣2（ab﹣ab2）+a2b]﹣3ab，其中a=12，b＝﹣4．30．（2022秋•海林市期末）先化简再求值：12a+2(a+3ab−13b2)−3(32a+2ab−13b2)，其中a、b满足|a﹣2|+（b+3）2＝0．31．（2022秋•万州区期末）化简求32a2b﹣2（ab2+1）−12(3a2b﹣ab2+4）的值，其中2（a﹣3）2022+|b+23|＝0．32．（2022秋•偃师市期末）已知：(x−2)2+|y +12|=0，求2（xy 2+x 2y ）﹣[2xy 2﹣3（1﹣x 2y ）]+2的值．33．（2022秋•沙坪坝区校级期中）先化简，再求值：2(x 2y−2x y 2)−[(−x 2y 2+4x 2y)−13(6x y 2−3x 2y 2)]，其中x 是最大的负整数，y 是绝对值最小的正整数．34．（2022秋•越秀区期末）已知代数式M ＝（2a 2+ab ﹣4）﹣2（2ab +a 2+1）．（1）化简M ；（2）若a ，b 满足等式（a ﹣2）2+|b +3|＝0，求M 的值．35．（2022秋•和平区校级期中）先化简再求值：若（a +3）2+|b ﹣2|＝0，求3ab 2﹣{2a 2b ﹣[5ab 2﹣（6ab 2﹣2a 2b ）]}的值．36．（2022秋•江都区期末）已知代数式A ＝x 2+xy ﹣12，B ＝2x 2﹣2xy ﹣1．当x ＝﹣1，y ＝﹣2时，求2A ﹣B 的值．37．已知：A ＝x −12y +2，B ＝x ﹣y ﹣1．（1）化简A ﹣2B ；（2）若3y ﹣2x 的值为2，求A ﹣2B 的值．38．（2022秋•邹平市校级期末）先化简，再求值：A ＝5xy 2﹣xy ，B =x y 2−2(32x y 2−0.5xy)．求A ﹣B ，其中x ，y 满足（x +1）2+|3﹣y |＝0．39．（2022秋•大丰区期末）已知A ＝2a 2b ﹣5ab 2，B ＝a 2b ﹣2ab 2﹣a ．（1）求A ﹣3B ．（2）求当a ＝2，b ＝﹣1时，A ﹣3B 的值．40．已知A＝2x2﹣3xy+y2+x+2y，B＝4x2﹣6xy+2y2﹣3x﹣y．当实数x、y满足|x﹣2|+（y−15）2＝0时，求B﹣2A的值．41．（2022秋•榆阳区校级期末）已知A＝2a2b﹣ab﹣2a，B＝a2b﹣a+3ab．（1）化简：A﹣2（A﹣B）；（结果用含a、b的代数式表示）（2）当a=−27，b＝3时，求A﹣2（A﹣B）的值．42．（2022秋•河池期末）已知，A＝3ab+a﹣2b，B＝2ab﹣b．（1）化简：2A﹣3B；（2）当b＝2a时，求2A﹣3B+4的值．43．（2023春•莱芜区月考）已知A ＝6a 2+2ab +7，B ＝2a 2﹣3ab ﹣1．（1）计算：2A ﹣（A +3B ）；（2）当a ，b 互为倒数时，求2A ﹣（A +3B ）的值．44．（2021秋•沂源县期末）已知多项式x 2+ax ﹣y +b 与bx 2﹣3x +6y ﹣3差的值与字母x 的取值无关，求代数式3（a 2﹣2ab ﹣b 2）﹣4（a 2+ab +b 2）的值．45．（2022秋•大竹县校级期末）已知代数式x 2+ax ﹣（2bx 2﹣3x +5y +1）﹣y +6的值与字母x 的取值无关，求13a 3−2b 2−14a 3+3b 2的值．46．（2022秋•利川市校级期末）若代数式（2x2+ax﹣y+6）﹣（2bx2﹣3x+5y﹣1）的值与字母x的取值无关，求代数式5ab2﹣[a2b+2（a2b﹣3ab2）]的值．47．（2022秋•沙坪坝区校级期末）已知A＝x2+ax﹣y，B＝bx2﹣x﹣2y，当A与B的差与x的取值无关时，求代数式3a2b−[2a b2−4(ab−34a2b)]+2a b2的值．48．（2022秋•沧州期末）已知A＝2x2+3xy﹣2x，B＝x2﹣xy+y2．（1）求2A﹣4B；（2）如果x，y满足（x﹣1）2+|y+2|＝0，求2A﹣4B的值；（3）若2A﹣4B的值与x的取值无关，求y的值．49．（2022秋•河北期末）已知一个多项式（3x2+ax﹣y+6）﹣（﹣6bx2﹣4x+5y﹣1）．（1）若该多项式的值与字母x的取值无关，求a，b的值；（2）在（1）的条件下，先化简多项式3ab2﹣[5a2b+2（ab2−12）+ab2]+6a2b，再求它的值．50．（2022秋•邗江区校级期末）已知关于x的代数式2x2−12bx2﹣y+6和ax+17x﹣5y﹣1的值都与字母x的取值无关．（1）求a，b的值．（2）若A＝4a2﹣ab+4b2，B＝3a2﹣ab+3b2，求4A+[（2A﹣B）﹣3（A+B）]的值．。

整式的化简求值解答题（50题）题型一先化简，再直接代入求值1．（2024春•靖江市校级月考）先化简，再求值：6y2﹣（2x2﹣y）+2（x2﹣3y2），其中x＝﹣2023，y＝2024．【分析】先去括号，再合并同类项，最后将y＝2024，代入求值即可．【解答】解：6y2﹣（2x2﹣y）+2（x2﹣3y2）＝6y2﹣2x2+y+2x2﹣6y2＝y，当y＝2024时，原式＝2024．【点评】本题考查了整式的化简求值，熟练掌握整式的运算法则是关键．2．先化简再求值：2x2y―[xy2+3(x2y―13xy2)]，其中x=12，y＝2．【分析】先化简整式，再代入求值．【解答】解：原式＝2x2y﹣（xy2+3x2y﹣xy2）＝2x2y﹣3x2y＝﹣x2y．当x=12，y＝2时，原式＝﹣（12）2×2=―14×2=―1 2．【点评】本题考查了整式的化简求值，掌握去括号法则、合并同类项法则及有理数的混合运算是解决本题的关键．3．（2023秋•吉州区期末）先化简，再求值：（x2y﹣2xy2）﹣3（2xy2﹣x2y），其中x=12，y＝﹣1．【分析】原式去括号合并得到最简结果，把x与y的值代入计算即可求出值．【解答】解：原式＝x2y﹣2xy2﹣6xy2+3x2y＝4x2y﹣8xy2，当x=12，y＝﹣1时，原式＝4×14×（﹣1）﹣8×12×（﹣1）2＝﹣1﹣4＝﹣5．【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．4．（2024春•开福区校级月考）先化简，再求值：2（﹣2x2+xy﹣y2）﹣（﹣4x2+4xy﹣2y2），其中x＝3，y ＝﹣1．【分析】首先去括号，然后合并同类项，化简后，再代入x、y的值求解即可．【解答】解：2（﹣2x2+xy﹣y2）﹣（﹣4x2+4xy﹣2y2）＝﹣4x2+2xy﹣2y2+4x2﹣4xy+2y2＝﹣2xy，当x＝3，y＝﹣1时，原式＝﹣2×3×（﹣1）＝6．【点评】本题考查了整式的加减与化简求值，熟练掌握整式的运算法则是关键．5．（2023秋•秦淮区期末）先化简，再求值：7a2b+（﹣4a2b+5ab2）﹣（2a2b﹣3ab2），其中a＝﹣1，b＝2．【分析】先进行整式的化简，再代入求值即可．【解答】解：7a2b+（﹣4a2b+5ab2）﹣（2a2b﹣3ab2），＝7a2b﹣4a2b+5ab2﹣2a2b+3ab2＝a2b+8ab2当a＝﹣1，b＝2时，原式＝（﹣1）2×2+8×（﹣1）×22＝2﹣32＝﹣30．【点评】本题考查了整式的加减，解决本题的关键是先化简．6．（2023•青秀区校级开学）先化简，再求值：4x+2（3y2﹣2x）﹣3（2x﹣y2），其中x＝2，y＝﹣2．【分析】原式去括号合并得到最简结果，把x与y的值代入计算即可求出值．【解答】解：原式＝4x+6y2﹣4x﹣6x+3y2＝﹣6x+9y2，当x＝2，y＝﹣2时，原式＝﹣6×2+9×（﹣2）2＝﹣12+36＝24．7．（2024春•东坡区期末）先化简，再求值：(2xy2+x3y)―[(4x2y2―xy2)+12(―8x2y2+4x3y)]，其中x＝﹣1，y=1 2．【分析】原式去括号合并得到最简结果，把x与y的值代入计算即可求出值．【解答】解：原式＝2xy2+x3y﹣4x2y2+xy2+4x2y2﹣2x3y＝3xy2﹣x3y，当x＝﹣1，y=12时，原式＝3×（﹣1）×（12）2﹣（﹣1）3×12=―34+12=―14．【点评】此题考查了整式的加减﹣化简求值，熟练掌握去括号法则与合并同类项法则是解本题的关键．7．（2023秋•南海区校级期末）先化简，再求值：（2x2﹣2y2）﹣3（x2y2+x2）+3（x2y2+y2），其中x＝﹣1，y＝2．【分析】将代数式去括号，合并同类项，从而将整式化为最简形式，然后把x、y的值代入即可．【解答】解：原式＝2x 2﹣2y 2﹣3x 2y 2﹣3x 2+3x 2y 2+3y 2＝﹣x 2+y 2；当x ＝﹣1，y ＝2时，原式＝﹣（﹣1）2+22＝﹣1+4＝3．【点评】本题主要考查了整式的加减运算．整式的加减运算实际上就是去括号、合并同类项．8．（2023秋•梁子湖区期末）先化简，再求值：5x 2―[2xy ―3(13xy +2)+4x 2]，其中x =―2，y =12．【分析】先将原式去括号、合并同类项，再把x ＝﹣2，y =12代入化简后的式子，计算即可．【解答】解：5x 2―[2xy ―3(13xy +2)+4x 2]＝5x 2﹣（2xy ﹣xy ﹣6+4x 2）＝5x 2﹣2xy+x y +6﹣4x 2＝（5x 2﹣4x 2）+（﹣2xy+xy ）+6＝x 2﹣xy+6，当x =―2，y =12时，原式=(―2)2―(―2)×12+6=4+1+6＝11．【点评】本题考查了整式的化简求值．整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．9．先化简，再求值：2（ab ―32a 2+a ﹣b 2）﹣3（a ﹣a 2+23ab ），其中a ＝5，b ＝﹣2．【分析】先化简整式，再代入求值．【解答】解：2（ab ―32a 2+a ﹣b 2）﹣3（a ﹣a 2+23ab ）＝2ab ﹣3a 2+2a ﹣2b 2﹣3a +3a 2﹣2ab＝﹣a ﹣2b 2．当a ＝5，b ＝﹣2时，原式＝﹣5﹣2×（﹣2）2＝﹣5﹣2×4＝﹣5﹣8＝﹣13．【点评】本题主要考查了整式的化简求值，掌握去括号法则、合并同类项法则及有理数的混合运算是解决本题的关键．10．（2024春•昭通期末）先化简，再求值：（3x2﹣3x2y﹣2xy2）﹣2（x2﹣xy2+y3）+3（x2y﹣y3），其中x ＝3，y＝﹣2．【分析】根据整式混合运算法则进行计算．【解答】解：原式＝3x2﹣3x2y﹣2xy2﹣2x2+2xy2﹣2y3+3x2y﹣3y3，＝x2﹣5y3，当x＝3，y＝﹣2时，原式＝32﹣5×（﹣2）3＝49．【点评】本题考查了整式的加减﹣化简求值，熟练掌握整式混合运算法则是解题的关键．11．（2023秋•雨花区期末）先化简再求值：3（x2﹣2x2y）﹣3x2+2y﹣2（x2y+y），其中x=12，y＝﹣3．【分析】直接去括号，再合并同类项，即可化简，把已知数据代入得出答案．【解答】解：3（x2﹣2x2y）﹣3x2+2y﹣2（x2y+y）＝3x2﹣6x2y﹣3x2+2y﹣2x2y﹣2y＝﹣8x2y，当x=12，y＝﹣3时，原式＝﹣8x2y＝﹣8×（12）2×（﹣3）＝﹣8×14×（﹣3）＝6．【点评】本题主要考查了整式的加减—化简求值，掌握整式的加减—化简方法是关键．12．（2023秋•绿园区期末）先化简，再求值：12m―(2m―23n2)+(―32m+13n2)，其中m=―14，n=―1 2．【分析】先去括号，然后合并同类项，再代入求值．【解答】解：原式=12m―2m+23n2―32m+13n2＝n2﹣3m，当m=―14，n=―12时，原式＝n2﹣3m＝（―12）2﹣3×（―14）=14+34＝1．【点评】本题考查了整式的加减—化简求值，熟悉去括号和合并同类项法则是解题的关键．13．（2023秋•公安县期中）先化简，再求值：4a2b﹣[﹣2ab2﹣2（ab﹣ab2）+a2b]﹣3ab，其中a=12，b＝﹣4．【分析】首先去括号进而合并同类项，再把a，b的值代入计算求出答案即可．【解答】解：4a2b﹣[﹣2ab2﹣2（ab﹣ab2）+a2b]﹣3ab＝4a2b﹣（﹣2ab2﹣2ab+2ab2+a2b）﹣3ab＝4a2b+2ab﹣a2b﹣3ab＝3a2b﹣ab；当a=12，b＝﹣4时，原式=3×(12)2×(―4)―12×(―4)=―3+2=―1．14．（2023秋•陕州区期中）先化简，再求值3x2y―2(x2y+14xy2)―2(xy2―xy)，其中x=12，y＝﹣2．【分析】原式去括号合并得到最简结果，把x与y的值代入计算即可求出值．【解答】解：3x2y―2(x2y+14xy2)―2(xy2―xy)=3x2y―2x2y―12xy2―2xy2―2xy=xy2―52xy2+2xy把x=12，y＝﹣2代入原式=(12)2×(―2)―52×12×(―2)2+2×12×(―2)=―712．【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．15．（2023秋•沈北新区期中）化简并求值．（1）2（2x﹣3y）﹣（3x+2y+1），其中x＝2，y＝﹣0.5（2）﹣（3a2﹣4ab）+[a2﹣2（2a+2ab）]，其中a＝﹣2．【分析】（1）原式去括号合并得到最简结果，将x与y的值代入计算即可求出值；（2）原式去括号合并得到最简结果，将a的值代入计算即可求出值．【解答】解：（1）原式＝4x﹣6y﹣3x﹣2y﹣1＝x﹣8y﹣1，将x＝2，y＝﹣0.5代入，得原式＝x﹣8y﹣1＝2﹣8×（﹣0.5）﹣1＝2+4﹣1＝5；（2）原式＝﹣3a2+4ab+a2﹣4a﹣4ab＝﹣2a2﹣4a，当a＝﹣2时，原式＝﹣8+8＝0．【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．题型二先化简，再整体代入求值16．（2023秋•范县期中）已知m+4n＝﹣1．求（6mn+7n）+[8m﹣（6mn+7m+3n）]的值．【分析】化简整理代数式，整体代入求值．【解答】解：∵m+4n＝﹣1．∴（6mn+7n）+[8m﹣（6mn+7m+3n）]＝6mn+7n+（8m﹣6mn﹣7m﹣3n）＝6mn+7n+8m﹣6mn﹣7m﹣3n＝4n+m＝﹣1．【点评】本题考查了整式的化简求值，解题的关键是掌握整体代入求值．17．先化简，再求值．若m2+3mn＝﹣5，则代数式5m2﹣[5m2﹣（2m2﹣mn）﹣7mn+7]的值．【分析】原式去括号，合并同类项进行化简，然后利用整体思想代入求值．【解答】解：原式＝5m2﹣（5m2﹣2m2+mn﹣7mn+7）＝5m2﹣5m2+2m2﹣mn+7mm﹣7＝2m2+6mm﹣7，∵m2+3mn＝﹣5，∴原式＝2（m2+3mn）﹣7＝2×（﹣5）﹣7＝﹣10﹣7＝﹣17．【点评】本题考查整式的加减—化简求值，掌握合并同类项（系数相加，字母及其指数不变）和去括号的运算法则（括号前面是“+”号，去掉“+”号和括号，括号里的各项不变号；括号前面是“﹣”号，去掉“﹣”号和括号，括号里的各项都变号）是解题关键．18．（2023秋•潮南区期末）先化简，再求值：23(6a ―3ab)+(ab ―2a)―2(ab +b)，其中a ﹣b ＝9，ab ＝﹣6．【分析】原式去括号合并得到最简结果，把a ﹣b 及ab 的值代入计算即可求出值．【解答】解：原式＝4a ﹣2ab +ab ﹣2a ﹣2ab ﹣2b＝2a ﹣3ab ﹣2b ．∵a ﹣b ＝9，ab ＝﹣6，∴原式＝2（a ﹣b ）﹣3ab＝2×9﹣3×（﹣6）＝36．【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．19．已知x +y ＝6，xy ＝﹣4，求：（5x +2y ﹣3xy ）﹣（2x ﹣y +2xy ）的值．【分析】先去括号，合并同类项，再将x +y ＝6，xy ＝﹣4，整体代入进行计算即可．【解答】解：原式＝5x +2y ﹣3xy ﹣2x +y ﹣2xy＝3x +3y ﹣5xy＝3（x +y ）﹣5xy ，当x +y ＝6，xy ＝﹣4时，原式＝3×6﹣5×（﹣4）＝18+20＝38．【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．20．（2023秋•荔湾区期末）已知a 2+b 2＝3，ab ＝﹣2，求代数式（7a 2+3ab +3b 2）﹣2（4a 2+3ab +2b 2）的值．【分析】原式去括号，合并同类项进行化简，然后利用整体思想代入求值．【解答】解：原式＝7a 2+3ab +3b 2﹣8a 2﹣6ab ﹣4b 2＝﹣a 2﹣3ab ﹣b 2；当a 2+b 2＝3，ab ＝﹣2时，原式＝﹣（a 2+b 2）﹣3ab＝﹣3﹣3×（﹣2）＝﹣3+6＝3，∴原代数式的值为3．【点评】本题考查整式的加减—化简求值，掌握合并同类项（系数相加，字母及其指数不变）和去括号的运算法则（括号前面是“+”号，去掉“+”号和括号，括号里的各项不变号；括号前面是“﹣”号，去掉“﹣”号和括号，括号里的各项都变号），利用整体思想解题是关键．21．（2023秋•平昌县期末）先化简，再求值．已知代数式2（3x2﹣x+2y﹣xy）﹣3（2x2﹣3x﹣y+xy），其中x+y=67，xy＝﹣2．【分析】原式去括号，合并同类项进行化简，然后利用整体思想代入求值．【解答】解：原式＝6x2﹣2x+4y﹣2xy﹣6x2+9x+3y﹣3xy＝7x+7y﹣5xy，当x+y=67，xy＝﹣2时，原式＝7（x+y）﹣5xy＝7×67―5×（﹣2）＝6+10＝16．【点评】本题考查整式的加减—化简求值，掌握合并同类项（系数相加，字母及其指数不变）和去括号的运算法则（括号前面是“+”“+”号和括号，括号里的各项不变号；括号前面是“﹣”号，去掉“﹣”号和括号，括号里的各项都变号），利用整体思想代入求值是解题关键．22．有这样一道题“如果代数式5a+3b的值为﹣4，那么代数式2（a+b）+4（2a+b）的值是多少？”爱动脑筋的吴爱国同学这样来解：原式＝2a+2b+8a+4b＝10a+6b．我们把5a+3b看成一个整体，把式子5a+3b ＝﹣4两边乘以2得10a+6b＝﹣8．整体思想是中学数学解题中的一种重要思想方法，它在多项式的化简与求值中应用极为广泛，仿照上面的解题方法，完成下面问题：【简单应用】（1）已知a2﹣2a＝1，则2a2﹣4a+1＝ ．（2）已知m+n＝2，mn＝﹣4，求2（mn﹣3m）﹣3（2n﹣mn）的值．【拓展提高】（3）已知a2+2ab＝﹣5，ab﹣2b2＝﹣3，求代数式3a2+4ab+4b2的值．【分析】（1）根据a2﹣2a＝1，把2a2﹣4a+1化为2（a2﹣2a）+1，整体代入计算；（2）根据m+n＝2，mn＝﹣4，把2（mn﹣3m）﹣3（2n﹣mn）化为5mn﹣6（m+n），整体代入计算；（3）根据a2+2ab＝﹣5，ab﹣2b2＝﹣3，①×3﹣②×2得结果．【解答】解：（1）当a2﹣2a＝1时，2a2﹣4a+1＝2（a2﹣2a）+1＝3；故答案为：3；（2）当m+n＝2，mn＝﹣4时，2（mn﹣3m）﹣3（2n﹣mn）＝2mn﹣6m﹣6n+3mn＝5mn﹣6（m+n）＝﹣32；（3）∵a2+2ab＝﹣5①，ab﹣2b2＝﹣3②，①×3﹣②×2得3a2+6ab﹣（2ab﹣4b2）＝3a2+4ab+4b2＝﹣5×3﹣（﹣3）×2＝﹣9．【点评】本题考查了整式的加减—化简求值，掌握整体代入的思想，把每一个整式进行适当的变形是解题的关键．23．（2023秋•龙泉市期中）阅读材料：我们知道，4x﹣2x+x＝（4﹣2+1）x＝3x，类似地，我们把（a+b）看成一个整体，则4（a+b）﹣2（a+b）+（a+b）＝（4﹣2+1）（a+b）＝3（a+b）．“整体思想”是数学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．尝试应用整体思想解决下列问题：（1）把（a﹣b）2看成一个整体，合并2（a﹣b）2﹣6（a﹣b）2+3（a﹣b）2；（2）若a（x2﹣2y）+b（x2﹣2y）＝x2﹣2y，且x2﹣2y≠0，求a+b+2023的值；（3）若对于任意x都有（ax5+bx4+x3+x2+x）+（cx5+dx4+x3+x2+x）＝2（x3+x2+x）成立，且abcd≠0，比较ca与db的大小，并说明理由．【分析】（1）根据阅读材料提供的方法，将系数相加减即可合并；（2）根据阅读材料提供的方法，求出a+b，即可求出a+b+2023的值；（3）根据题意得到a＝﹣c，b＝﹣d，即可求出ca与db的值，从而解决问题．【解答】解：（1）原式＝（2﹣6+3）（a﹣b）2＝﹣（a﹣b）2；（2）∵（a+b）（x2﹣2y）＝（x2﹣2y），∴a+b＝1，∴a+b+2023＝1+2﹣23＝2024；（3）ca=db．理由如下：∵对于任意x都有（ax5+bx4+x3+x2+x）+（cx5+dx4+x3+x2+x）＝2（x3+x2+x）成立，∴对于任意x都有（a+c）x5+（b+d）x4+2x3+2x2+2x＝2（x3+x2+x）成立，∴a+c＝0，b+d＝0，∴a＝﹣c，b＝﹣d，∴ca=―1，db=―1，∴ca=db．【点评】本题考查合并同类项，代数式求值，理解整体思想，掌握合并同类项的基本方法是解题的关键．24．阅读理解：已知4a―52b＝1，求代数式2（a﹣b）+3（2a﹣b）的值．解：因为4a―52b＝1，所以原式=2a―2b+6a―3b=8a―5b=2(4a―52b)=2×1=2．仿照以上解题方法，完成下面的问题：（1）已知a﹣b＝﹣3，求3（a﹣b）﹣a+b+1的值；（2）已知a2+2ab＝2，ab﹣b2＝1，求2a2+5ab﹣b2的值．【分析】（1）把（a﹣b）看成一个整体，先变形要求值代数式，再整体代入；（2）可变形已知，整体代入求值．【解答】解：（1）3（a﹣b）﹣a+b+1＝3（a﹣b）﹣（a﹣b）+1＝2（a﹣b）+1．当a﹣b＝﹣3时，原式＝2×（﹣3）+1＝﹣6+1＝﹣5．（2）法一、∵a2+2ab＝2，ab﹣b2＝1，∴2a2+4ab＝4，∴2a2+4ab+ab﹣b2＝5．即2a2+5ab﹣b2＝5．法二、∵a2+2ab＝2，ab﹣b2＝1，∴a2＝2﹣2ab，﹣b2＝1﹣ab．∴2a2+5ab﹣b2＝2（2﹣2ab）+5ab+1﹣ab＝4﹣4ab+5ab+1﹣ab＝5．【点评】本题主要考查了整式的化简求值，掌握整式的运算法则和整体的思想方法是解决本题的关键．25．（2024春•道里区校级期中）【知识呈现】我们可把5（x﹣2y）﹣3（x﹣2y）+8（x﹣2y）﹣4（x﹣2y）中的“x﹣2y”看成一个字母a，使这个代数式简化为5a﹣3a+8a﹣4a，“整体思想”是中学数学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．在数学中，常常用这样的方法把复杂的问题转化为简单问题．【解决问题】（1）上面【知识呈现】中的问题的化简结果为 ；（用含x、y的式子表示）（2）若代数式x2+x+1的值为3，求代数式2x2+2x﹣5的值为 ；【灵活运用】应用【知识呈现】中的方法解答下列问题：（3）已知a﹣2b＝7，2b﹣c的值为最大的负整数，求3a+4b﹣2（3b+c）的值．【分析】（1）令“x﹣2y”＝a，则原式化为5a﹣3a+8a﹣4a，然后合并同类项，最后将a＝x﹣2y代入即可；（2）将2x2+2x﹣5变形为2（x2+x）﹣5，然后整体代入求值即可；（3）由题意得出2b﹣c＝﹣1，结合a﹣2b＝7即可得出a﹣c＝6，将3a+4b﹣2（3b+c）变形为（a﹣2b）+2（a﹣c），然后代入求值即可．【解答】解：（1）令“x﹣2y”＝a，则5（x﹣2y）﹣3（x﹣2y）+8（x﹣2y）﹣4（x﹣2y）＝5a﹣3a+8a﹣4a＝（5﹣3+8﹣4）a＝6a＝6（x﹣2y）＝6x﹣12y，故答案为：6x﹣12y；（2）由题意得，x2+x+1＝3，∴x2+x＝2，∴2x2+2x﹣5＝2（x2+x）﹣5＝2×2﹣5＝﹣1，故答案为：﹣1；（3）∵2b﹣c的值为最大的负整数，∴2b﹣c＝﹣1①，∵a﹣2b＝7②，①+②，得a﹣c＝6，∴3a+4b﹣2（3b+c）＝3a+4b﹣6b﹣2c＝3a﹣2b﹣2c＝（a﹣2b）+（2a﹣2c）＝（a﹣2b）+2（a﹣c）＝7+2×6＝19．【点评】本题考查了整体思想，合并同类项，负整数，理解题意，熟练掌握整体思想是解题的关键．26．（2023秋•祁阳县期末）图是湘教版七年级上册数学教材65页的部分内容．明明同学在做作业时采用的方法如下：由题意得3（a2+2a）+2＝3×1+2＝5，所以代数式3（a2+2a）+2的值为5．【方法运用】：（1）若代数x2﹣2x+3的值为5，求代数式3x2﹣6x﹣1的值；（2）当x＝1时，代数式ax3+bx+5的值为8．当x＝﹣1，求代数式ax3+bx﹣6的值；（3）若x2﹣2xy+y2＝20，xy﹣y2＝6，求代数式x2﹣3xy+2y2的值．【分析】（1）根据题意得出x2﹣2x+3＝5，求出x2﹣2x＝2，变形后代入，即可求出答案；（2）根据题意求出a+b+5＝8，求出a+b＝3，再把x＝﹣1代入代数式，最后整体代入，即可求出答案；（3）代数式x2﹣2xy+y2＝20减去代数式xy﹣y2＝6，即可得出答案．【解答】解：（1）根据题意得：x2﹣2x+3＝5，即x2﹣2x＝2，所以3x2﹣6x﹣1＝3（x2﹣2x）﹣1＝3×2﹣1＝6﹣1＝5；（2）∵当x＝1时，代数式ax3+bx+5的值为8，∴a+b+5＝8，∴a+b＝3，当x＝﹣1时，ax3+bx﹣6＝a×（﹣1）3+b×（﹣1）﹣6＝﹣a﹣b﹣6＝﹣（a+b）﹣6＝﹣3﹣6＝﹣9；（3）∵①x2﹣2xy+y2＝20，②xy﹣y2＝6，∴①﹣②，得x2﹣2xy+y2﹣（xy﹣y2）＝20﹣6，整理得：x2﹣3xy+2y2＝14．【点评】本题考查了求代数式的值，能够整体代入是解此题的关键．27．（2023秋•惠东县期中）有这样一道题“如果式子5a+3b的值为﹣4，那么式子2（a+b）+4（2a+b）的值是多少？”爱动脑筋的佳佳同学这样来解：原式＝2a+2b+8a+4b＝10a+6b．我们把5a+3b看成一个整体，则原式＝2（5a+3b）＝2×（﹣4）＝﹣8．整体思想是中学数学解题中的一种重要思想方法，它在多项式的化简与求值中应用极为广泛，仿照佳佳的解题方法，完成下面问题：（1）已知a2﹣2a＝1，则2a2﹣4a+1＝　；（2）已知m+n＝2，mn＝﹣4，求2（mn﹣3m）﹣3（2n﹣mn）的值；（3）已知a2+2ab＝﹣5，ab﹣2b2＝﹣3，求3a2+4ab+4b2的值．【分析】（1）根据a2﹣2a＝1，把2a2﹣4a+1化为2（a2﹣2a）+1，整体代入计算；（2）根据m+n＝2，mn＝﹣4，把2（mn﹣3m）﹣3（2n﹣mn）化为5mn﹣6（m+n），整体代入计算；（3）根据a2+2ab＝﹣5，ab﹣2b2＝﹣3，①×3﹣②×2得结果．【解答】解：（1）当a2﹣2a＝1时，2a2﹣4a+1＝2（a2﹣2a）+1＝3；故答案为：3；（2）当m+n＝2，mn＝﹣4时，2（mn﹣3m）﹣3（2n﹣mn）＝2mn﹣6m﹣6n+3mn＝5mn﹣6（m+n）＝﹣32；（3）∵a2+2ab＝﹣5①，ab﹣2b2＝﹣3②，①×3﹣②×2得3a2+6ab﹣（2ab﹣4b2）＝3a2+4ab+4b2＝﹣5×3﹣（﹣3）×2＝﹣9．【点评】本题考查了整式的加减—化简求值，掌握整体代入的思想，把每一个整式进行适当的变形是解题的关键．题型三先求字母的值，再代入求值28．（2024春•海淀区校级期中）先化简，再求值：已知（a﹣2）2+|b+3|＝0，求10a2b﹣[2ab2﹣2（ab﹣5a2b）]的值．【分析】根据整式加减的计算法则进行化简，然后根据非负数的性质求出a、b再代入求值即可．【解答】解：原式＝10a2b﹣（2ab2﹣2ab+10a2b）＝10a2b﹣2ab2+2ab﹣10a2b＝﹣2ab2+2ab，∵（a﹣2）2+|b+3|＝0，∴a﹣2＝0，b+3＝0，∴a＝2，b＝﹣3，∴原式＝﹣2×2×（﹣3）2+2×2×（﹣3）＝﹣36+（﹣12）＝﹣48．【点评】本题考查整式加减的化简求值，解题关键是熟知非负数的性质以及整式加减的计算法则．29．（2023秋•镇江期末）先化简，再求值：﹣2xy+（5xy﹣3x2+1）﹣3（2xy﹣x2），其中x、y满足|x+2|+（y﹣1）2＝0．【分析】根据整式的加减运算法则将﹣2xy+（5xy﹣3x2+1）﹣3（2xy﹣x2）化简，再根据绝对值和平方式的非负性求得x、y x、y的值代入化简后的式子进行计算，即可解题．【解答】解：﹣2xy+（5xy﹣3x2+1）﹣3（2xy﹣x2）＝﹣2xy+5xy﹣3x2+1﹣6xy+3x2＝﹣3xy+1，∵x、y满足|x+2|+（y﹣1）2＝0．∴|x+2|＝0，（y﹣1）2＝0，即x+2＝0，y﹣1＝0，解得x＝﹣2，y＝1，将x＝﹣2，y＝1代入﹣3xy+1中，有﹣3xy+1＝﹣3×（﹣2）×1+1＝7．【点评】本题考查整式的化简求值，能化简是解题的关键．30．（2023秋•海林市期末）先化简再求值：12a+2(a+3ab―13b2)―3(32a+2ab―13b2)，其中a、b满足|a﹣2|+（b+3）2＝0．【分析】先去括号，然后合并同类项进行化简，根据非负数的性质求出a、b的值代入化简后的结果进行计算即可．【解答】解：原式=12a+2a+6ab―23b2―92a―6ab+b2=―2a+13b2，∵|a﹣2|+（b+3）2＝0，∴a﹣2＝0，b+3＝0，∴a＝2，b＝﹣3，当a＝2，b＝﹣3时，原式＝﹣2×2+13（﹣3）2＝﹣4+3＝﹣1．【点评】本题考查了整式的加减——化简求值，涉及了去括号法则，合并同类项法则，非负数的性质等，熟练掌握各运算的运算法则以及非负数的性质是解题的关键．31．（2023秋•罗山县期末）已知：(x―2)2+|y+12|=0，求2（xy2+x2y）﹣[2xy2﹣3（1﹣x2y）]+2的值．【分析】根据非负数的性质，可求出x、y的值，然后将代数式化简再代值计算．【解答】解：原式＝2xy2+2x2y﹣（2xy2﹣3+3x2y）+2＝2xy2+2x2y﹣2xy2+3﹣3x2y+2＝（2﹣2）xy2+（2﹣3）x2y+（3+2）＝﹣x2y+5；∵（x+2）2≥0，|y―12|≥0，又∵(x―2)2+|y+12|=0，∴x﹣2＝0，y+12=0，∴x＝2，y=―1 2，∴原式＝﹣22×(―12)+5＝2+5＝7．【点评】本题考查整式的化简求值，它涉及对运算的理解以及运算技能的掌握两个方面，也是一个常考的题材．32．（2024春•东坡区期末）先化简，再求值：（2x2y﹣5xy）﹣2（x2y﹣xy），其中x，y满足|x―13|+（y+3）2＝0．【分析】原式去括号合并得到最简结果，利用非负数的性质求出x与y的值，代入计算即可求出值．【解答】解：原式＝2x2y﹣5xy﹣2x2y+2xy＝﹣3xy，|x―13|+(y+3)2=0．x―13=0，y+3＝0，∴x=13，y＝﹣3，∴原式=―3×13×(―3)=3．【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．33．（2023秋•沙坪坝区校级期中）先化简，再求值：2(x2y―2xy2)―[(―x2y2+4x2y)―13(6xy2―3x2y2)]，其中x是最大的负整数，y是绝对值最小的正整数．【分析】去括号，合并同类项，代入数据求值．【解答】解：∵x y是绝对值最小的正整数，∴x＝﹣1，y＝1，∴2(x2y―2xy2)―[(―x2y2+4x2y)―13(6xy2―3x2y2)]＝2x2y﹣4xy2﹣（﹣x2y2+4x2y﹣2xy2+x2y2）＝2x2y﹣4xy2+x2y2﹣4x2y+2xy2﹣x2y2＝﹣2x2y﹣2xy2＝﹣2×（﹣1）2×1﹣2×（﹣1）×12＝﹣2+2＝0．∴化简后结果为：﹣2x2y﹣2xy2，值为：0．【点评】本题考查了整式的化简求值，解题的关键是掌握整式的化简．34．（2023秋•越秀区期末）已知代数式M＝（2a2+ab﹣4）﹣2（2ab+a2+1）．（1）化简M；（2）若a，b满足等式（a﹣2）2+|b+3|＝0，求M的值．【分析】（1）直接利用去括号，进而合并同类项即可得出答案；（2）结合非负数的性质得出a，b的值，代入a，b的值得出答案．【解答】解：（1）M＝2a2+ab﹣4﹣4ab﹣2a2﹣2＝﹣3ab﹣6；（2）∵（a﹣2）2+|b+3|＝0，∴a﹣2＝0，b+3＝0，解得：a＝2，b＝﹣3，故M＝﹣3×2×（﹣3）﹣6＝18﹣6＝12．【点评】此题主要考查了整式的加减—化简求值，正确合并同类项是解题关键．35．（2023秋•和平区校级期中）先化简再求值：若（a+3）2+|b﹣2|＝0，求3ab2﹣{2a2b﹣[5ab2﹣（6ab2﹣2a2b）]}的值．【分析】先去括号、合并同类项，再根据非负数的性质求出a、b，最后代入化简后的整式求值．【解答】解：3ab2﹣{2a2b﹣[52﹣（6ab2﹣2a2b）]}＝3ab2﹣[2a2b﹣（5ab2﹣6ab2+2a2b）]＝3ab2﹣（2a2b﹣5ab2+6ab2﹣2a2b）＝3ab2﹣2a2b+5ab2﹣6ab2+2a2b＝2ab2．∵（a+3）2+|b﹣2|＝0，又∵（a+3）2≥0，|b﹣2|≥0，∴a+3＝0，b﹣2＝0．∴a＝﹣3，b＝2．当a＝﹣3，b＝2时，原式＝2×（﹣3）×22＝2×（﹣3）×4＝﹣24．【点评】本题考查了整式的化简﹣求值，掌握去括号法则、合并同类项法则、非负数的性质及有理数的混合运算是解决本题的关键．题型四先列式化简，再求值36．（2024春•莘县校级期末）已知A＝2x2﹣x﹣1，B＝3x2﹣2x﹣1，C＝x2﹣2x，求A﹣（B﹣C）的值，其中x=―1 2．【分析】把A、B、C的式子代入A﹣（B﹣C）后，先去括号，合并同类项，把多项式化为最简形式后，把x=―12代入计算即可．【解答】解：∵A＝2x2﹣x﹣1，B＝3x2﹣2x﹣1，C＝x2﹣2x，∴A﹣（B﹣C）＝2x2﹣x﹣1﹣[3x2﹣2x﹣1﹣（x2﹣2x）]＝2x2﹣x﹣1﹣（3x2﹣2x﹣1﹣x2+2x）＝2x2﹣x﹣1﹣3x2+2x+1+x2﹣2x＝﹣x，当x=―12时，原式＝﹣（―12）=12．37．已知：A＝x―12y+2，B＝x﹣y﹣1．（1）化简A﹣2B；（2）若3y﹣2x的值为2，求A﹣2B的值．【分析】（1）把A、B表示的代数式代入A﹣2B中，计算求值即可；（2）利用等式的性质，变形已知，整体代入（1）的结果中求值即可．【解答】解：∵A＝x―12y+2，B＝x﹣y﹣1，∴A﹣2B＝x―12y+2﹣2（x﹣y﹣1）＝x―12y+2﹣2x+2y+2＝﹣x+32y+4；（2）当3y﹣2x＝2时，即﹣x+32y＝1．＝﹣x+32y+4＝1+4＝5．【点评】本题考查了整式的加减、整体代入的思想方法，掌握去括号、合并同类项法则是解决本题的关键．38．（2023秋•襄都区期末）已知多项式A＝2a2+3ab﹣1，B＝a2+ab，A﹣2B﹣C＝0．（1）求多项式C．（2）当a＝2，b＝﹣3时，求多项式C的值．【分析】（1）直接由A﹣2B﹣C＝0得到C＝A﹣2B，再把A、B多项式代入求出结果；（2）将a＝2，b＝﹣3代入多项式C中，求值即可．【解答】解：（1）∵A﹣2B﹣C＝0∴C＝A﹣2B，∴C＝2a2+3ab﹣1﹣2（a2+ab），整理得C＝ab﹣1；（2）把a＝2，b＝﹣3代入ab﹣1中，得C＝2×（﹣3）﹣1＝﹣7．【点评】本题考查了整式的加减，关键运用代入法来解答．39．（2023秋•大丰区期末）已知A＝2a2b﹣5ab2，B＝a2b﹣2ab2﹣a．（1）求A﹣3B．（2）求当a＝2，b＝﹣1时，A﹣3B的值．【分析】（1）先把A、B表示的代数式代入，然后化简求值；（2）把a、b的值代入化简的代数式，计算得结果．【解答】解：（1）∵A＝2a2b﹣5ab2，B＝a2b﹣2ab2﹣a，∴A﹣3B＝2a2b﹣5ab2﹣3（a2b﹣2ab2﹣a）＝2a2b﹣5ab2﹣3a2b+6ab2+3a＝﹣a2b+ab2+3a．（2）当a＝2，b＝﹣1时，A﹣3B＝﹣22×（﹣1）+2×（﹣1）2+3×2＝12．【点评】本题考查了整式的化简求值，掌握去括号法则、合并同类项法则是解决本题的关键．40．（2023秋•徐闻县期末）已知：M＝4x2y﹣3xy2，N＝3x2y﹣2xy2．（1）计算M﹣2N的值；（2）若单项式﹣2a1﹣2x b6与5a2b2﹣4y是同类项，求M﹣2N的值．【分析】（1）先去括号，然后合并同类项即可得到答案；（2）根据同类项的定义得到1﹣2x＝2，2﹣4y＝6，则x=―12，y=―1，据此代值计算即可．【解答】解（1）∵M＝4x2y﹣3xy2，N＝3x2y﹣2xy2，∴M﹣2N＝4x2y﹣3xy2﹣2（3x2y﹣2xy2）＝4x2y﹣3xy2﹣6x2y+4xy2＝﹣2x2y+xy2；（2）∵单项式﹣2a1﹣2x b6与5a2b2﹣4y是同类项，∴1﹣2x＝2，2﹣4y＝6，∴x=―12，y=―1，∴M―2N=―2×(―12)2×(―+(―12)×(―1)2=12―12=0．【点评】本题主要考查了整式的化简求值，同类项的定义，熟知整式的加减计算法则是解题的关键．41．（2023秋•榆阳区校级期末）已知A＝2a2b﹣ab﹣2a，B＝a2b﹣a+3ab．（1）化简：A﹣2（A﹣B）；（结果用含a、b的代数式表示）（2）当a=―27，b＝3时，求A﹣2（A﹣B）的值．【分析】（1）先去括号，合并同类项，然后把A，B的值代入化简后的式子，进行计算即可解答；（2）把a，b的值代入（1）中的结论，进行计算即可解答．【解答】解：（1）∵A＝2a2b﹣ab﹣2a，B＝a2b﹣a+3ab，∴A﹣2（A﹣B）＝A﹣2A+2B＝﹣A+2B＝﹣（2a2b﹣ab﹣2a）+2（a2b﹣a+3ab）＝﹣2a2b+ab+2a+2a2b﹣2a+6ab（2）当a=―27，b＝3时，A﹣2（A﹣B）＝7×（―27）×3＝﹣6．【点评】本题考查了整式的加减﹣化简求值，准确熟练地进行计算是解题的关键．42．（2023秋•河池期末）已知，A＝3ab+a﹣2b，B＝2ab﹣b．（1）化简：2A﹣3B；（2）当b＝2a时，求2A﹣3B+4的值．【分析】（1）将A＝3ab+a﹣2b，B＝2ab﹣b代入2A﹣3B，再进行化简即可求解；（2）由（1）可得2A﹣3B+4，再把b＝2a代入可求解．【解答】解：（1）∵A＝3ab+a﹣2b，B＝2ab﹣b，∴2A﹣3B＝2（3ab+a﹣2b）﹣3（2ab﹣b）＝6ab+2a﹣4b﹣6ab+3b＝2a﹣b；（2）由（1）知，2A﹣3B＝2a﹣b，∴2A﹣3B+4＝2a﹣b+4，∴当b＝2a时，原式＝2a﹣2a+4＝4．【点评】本题主要考查了整式的加减运算，掌握去括号法则和合并同类项法则是解题的关键．43．（2023春•莱芜区月考）已知A＝6a2+2ab+7，B＝2a2﹣3ab﹣1．（1）计算：2A﹣（A+3B）；（2）当a，b互为倒数时，求2A﹣（A+3B）的值．【分析】（1）把A、B代入2A﹣（A+3B）计算即可；（2）当a，b互为倒数时，ab＝1，根据（1）的计算结果，求出2A﹣（A+3B）的值即可．【解答】解：（1）∵A＝6a2+2ab+7，B＝2a2﹣3ab﹣1，∴2A﹣（A+3B）＝2A﹣A﹣3B＝A﹣3B＝（6a2+2ab+7）﹣3（2a2﹣3ab﹣1）＝6a 2+2ab +7﹣6a 2+9ab +3＝11ab +10．（2）当a ，b 互为倒数时，ab ＝1，2A ﹣（A +3B ）＝11ab +10＝11×1+10＝11+10＝21．【点评】此题主要考查了整式的加减﹣化简求值问题，解答此题的关键是要明确：给出整式中字母的值，求整式的值的问题，一般要先化简，再把给定字母的值代入计算，得出整式的值，不能把数值直接代入整式中计算．题型五 利用与某字母无关求整式的值44．（2023秋•南昌期末）如果关于x 、y 的代数式（2x 2+ax ﹣y +6）﹣（2bx 2﹣3x +5y ﹣1）的值与字母x 所取的值无关，试化简代数式a 3―2b 2―2(14a 3―3b 2)，再求值．【分析】对关于x 、y 的代数式去括号，合并同类项，化简后根据其值与字母x 所取的值无关列式求出a ，b 的值，然后对所求代数式去括号，合并同类项，化简后把a 、b 的值代入计算即可．【解答】解：（2x 2+ax ﹣y +6）﹣（2bx 2﹣3x +5y ﹣1）＝2x 2+ax ﹣y +6﹣2bx 2+3x ﹣5y +1＝（2﹣2b ）x 2+（a +3）x ﹣6y +7，∵代数式（2x 2+ax ﹣y +6）﹣（2bx 2﹣3x +5y ﹣1）的值与字母x 所取的值无关，∴2﹣2b ＝0，a +3＝0，解得：b ＝1，a ＝﹣3，a 3―2b 2―2(14a 3―3b 2) =a 3―2b 2―12a 3+6b 2 =12a 3+4b 2；当b ＝1，a ＝﹣3时，原式=12×(―3)3+4×12=―272+4=―192．【点评】此题主要考查了整式的加减﹣﹣化简求值，熟练掌握去括号法则和合并同类项法则是解题的关键．45．（2024春•萨尔图区校级期末）已知关于x的整式A＝x2+mx+1，B＝nx2+3x+2m（m，n为常数）．若整式A+B的取值与x无关，求m﹣n的值．【分析】将A＝x2+mx+1，B＝nx2+3x+2m分别代入A+B中，合并得出最简结果，根据A+B的取值与x无关，求出n，m的值，从而进一步求出m﹣n的值．【解答】解：∵A＝x2+mx+1，B＝nx2+3x+2m，∴A+B＝x2+mx+1+nx2+3x+2m＝（1+n）x2+（m+3）x+1+2m，∵整式A+B的取值与x无关，∴1+n＝0，m+3＝0，解得：n＝﹣1，m＝﹣3，则m﹣n＝﹣3﹣（﹣1）＝﹣3+1＝﹣2．【点评】本题主要考查了整式的加减法则，熟练掌握运算法则是解决本题的关键．46．（2023秋•沧州期末）已知A＝2x2+3xy﹣2x，B＝x2﹣xy+y2．（1）求2A﹣4B；（2）如果x，y满足（x﹣1）2+|y+2|＝0，求2A﹣4B的值；（3）若2A﹣4B的值与x的取值无关，求y的值．【分析】（1）直接将A＝2x2﹣2x，B＝x2﹣xy+y2代入计算即可；（2）先根据非负性求出x、y的值，再代入（1）中结果计算即可；（3）直接将10xy﹣4x﹣4y2转化为（10y﹣4）x﹣4y2计算y即可．【解答】解：（1）2A﹣4B＝2（2x2+3xy﹣2x）﹣4（x2﹣xy+y2）＝4x2+6xy﹣4x﹣4x2+4xy﹣4y2＝10xy﹣4x﹣4y2．（2）由题意可知：x﹣1＝0，y+2＝0，所以x＝1，y＝﹣2，原式＝10×1×（﹣2）﹣4×1﹣4×（﹣2）2＝﹣20﹣4﹣16＝﹣40．（3）因为2A﹣4B的值与x的取值无关，所以2A﹣4B＝10xy﹣4x﹣4y2＝2x（5y﹣2）﹣4y2，所以5y﹣2＝0，所以y=2 5．【点评】本题考查了整式的混合运算，熟练掌握运算法则是解题的关键．47．（2023秋•黄石港区期末）已知：关于x的多项式2（mx2﹣x―72）+4x2+3nx的值与x的取值无关．（1）求m，n的值；（2）求3（2m2﹣3mn﹣5m﹣1）+6（﹣m2+mn﹣1）的值．【分析】（1）先去括号，再合并同类项即可化简，再根据多项式2(mx2―x―72)+4x2+3nx的值与x的取值无关得出2m+4＝0，3n﹣2＝0，进行计算即可求解；（2）先去括号，再合并同类项即可化简，再代入m＝﹣2，n=23进行计算即可得出答案．【解答】解：（1）2(mx2―x―72)+4x2+3nx＝2mx2﹣2x﹣7+4x2+3nx＝（2m+4）x2+（3n﹣2）x﹣7，∵关于x的多项式2(mx2―x―72)+4x2+3nx的值与x的取值无关，∴2m+4＝0，3n﹣2＝0，∴m＝﹣2，n=2 3；（2）由（1）得：m＝﹣2，n=2 3，∴3（2m2﹣3mn﹣5m﹣1）+6（﹣m2+mn﹣1）＝6m2﹣9mn﹣15m﹣3﹣6m2+6mn﹣6＝﹣3mn﹣15m﹣9=―3×(―2)×23―15×(―2)―9＝4+30﹣9＝25．【点评】本题考查了整式的加减中的无关题型、整式的加减中的化简求值，熟练掌握整式的加减的运算法则是解此题的关键．48．（2023秋•金东区期末）已知A＝﹣3a2+7ab﹣3a﹣1，B＝a2﹣2ab+1；（1）当a＝2，b＝2024时，求A+3B的值．（2）若A+3B的值与a的取值无关，求b的值．【分析】（1）先去括号合并同类项，再代值计算即可解答；（2）根据已知可得含a项的系数为0，然后进行计算即可解答．【解答】解：（1）∵A＝﹣3a2+7ab﹣3a﹣1，B＝a2﹣2ab+1∴A+3B＝﹣3a2+7ab﹣3a﹣1+3a2﹣6ab+3＝ab﹣3a+2；把a＝2，b＝2024代入ab﹣3a+2，得ab﹣3a+2＝2×2024﹣3×2+2＝4044；（2）∵A+3B＝ab﹣3a+2＝（b﹣3）a+2，∵A+3B的值与a的值无关，∴b﹣3＝0∴b＝3．【点评】本题考查了整式的加减−化简求值，掌握整式的加减−化简方法是解题的关键．49．（2023秋•河北期末）已知一个多项式（3x2+ax﹣y+6）﹣（﹣6bx2﹣4x+5y﹣1）．（1）若该多项式的值与字母x a，b的值；（2）在（1）的条件下，先化简多项式3ab2﹣[5a2b+2（ab2―12）+ab2]+6a2b，再求它的值．【分析】（1）去括号，合并同类项将原式化为（3+6b）x2+（a+4）x﹣6y+7，再令x项的系数为0即可；（2）根据去括号、合并同类项将原式化简后，再代入求值即可．【解答】解：（1）原式＝3x2+ax﹣y+6+6bx2+4x﹣5y+1＝（3+6b）x2+（a+4）x﹣6y+7，∵该多项式的值与字母x的取值无关，∴3+6b＝0，a+4＝0，∴a＝﹣4，b=―1 2；（2）原式＝3ab2﹣（5a2b+2ab2﹣1+ab2）+6a2b ＝3ab2﹣5a2b﹣2ab2+1﹣ab2+6a2b＝a2b+1，当a＝﹣4，b=―12时，原式＝（﹣4）2×（―12）+1＝﹣8+1＝﹣7．【点评】本题考查整式的加减，掌握去括号、合并同类项法则是正确计算的前提．50．（2023秋•邗江区校级期末）已知关于x的代数式2x2―12bx2﹣y+6和ax+17x﹣5y﹣1的值都与字母x的取值无关．（1）求a，b的值．（2）若A＝4a2﹣ab+4b2，B＝3a2﹣ab+3b2，求4A+[（2A﹣B）﹣3（A+B）]的值．【分析】（1）先去括号，再合并同类项，然后根据代数式2x2―12bx2﹣y+6和ax+17x﹣5y﹣1的值都与字母x的取值无关得出关于a和b的方程，计算即可．（2）先将4A+[（2A﹣B）﹣3（A+B）]去括号，合并同类项，再将A＝4a2﹣ab+4b2，B＝3a2﹣ab+3b2代入化简，然后将a与b的值代入计算即可．【解答】解：（1）2x2―12bx2﹣y+6＝（2―12b）x2﹣y+6，ax+17x﹣5y﹣1＝（a+17）x﹣5y﹣1，∵关于x的代数式2x2―12bx2﹣y+6和ax+17x﹣5y﹣1的值都与字母x的取值无关，∴2―12b＝0，a+17＝0，∴a＝﹣17，b＝4．（2）4A+[（2A﹣B）﹣3（A+B）]＝4A+2A﹣B﹣3A﹣3B＝3A﹣4B，∵A＝4a2﹣ab+4b2，B＝3a2﹣ab+3b2，∴3A﹣4B＝3（4a2﹣ab+4b2）﹣4（3a2﹣ab+3b2）＝12a2﹣3ab+12b2﹣12a2+4ab﹣12b2＝ab，由（1）知a＝﹣17，b＝4，∴原式＝（﹣17）×4＝﹣68．【点评】本题考查了整式的加减﹣化简求值，熟练掌握整式的加减的运算法则是解题的关键．。

整式求值经典题型（九大题型）【题型1 直接代入】【题型2 整体代入-配系数】【题型3整体代入-奇次项为相反数】【题型4 整体构造代入】【题型5不含无关】【题型6 化简求值】【题型7 绝对值化简求值】【题型8 非负性求值】【题型9 定义求值】【题型1 直接代入】【典例1】根据下列a，b的值，分别求代数式a2―4ba的值．(1)a=5，b=25(2)a=―3，b=2【变式1-1】设a的相反数是2,b是绝对值最小的数，c是倒数等于自身的有理数，则a―b+c的值为（）A．32B．―1C．―1或―3D．32或―12【变式1-2】若|x|=4，|y|=3，且x+y>0，则x―y的值是（）A．1或7B．1或―7C．―1或7D．―1或―7【变式1-3】已知|x|=4，|y|=12，且x+y<0，则xy的值为．【题型2 整体代入-配系数】【典例2】当代数式x3+3x+1的值为2022时，代数式2x3+6x―3的值为（）A．2022B．4037C．4039D．2019【变式2-1】若代数式2x2+3x的值是5，则代数式4x2+6x―9的值是（）A．10B．1C．―4D．―8【变式2-2】已知2y2+y―2的值为3，则4y2+2y+1值为（）A．10B．11C．10或11D．3或1【变式2-3】若a2+3a―4=0，则2a2+6a―3=．【变式2-4】已知x2+5x―3的值是4，则多项式2x2+10x―4的值是．【题型3整体代入-奇次项为相反数】【典例3】当x=1时，代数式ax5+bx3+cx―7的值为12，则当x=―1时，求代数式ax5+bx3+cx―7的值．【变式3-1】当x=3时，代数式ax2025+bx2013―1的值是8，则当x=―3时，这个代数式的值是（）A．―10B．8C．9D．―8【变式3-2】当x=―2时，代数式ax3+bx―4的值是―2026，当x=2时，代数式ax3+bx―4的值为．【题型4 整体构造代入】【典例4】若a―5=3b，则(a+2b)―(2a―b)的值为．【变式4-1】已知m―n=3，p+q=2，则(m+p)―(n―q)的值为．【题型5不含无关】【典例5】已知多项式M=2x2―3xy+2y―2x2+x―xy+1．(1)先化简，再求M的值，其中x=1，y=2；(2)若多项式M与字母y的取值无关，求x的值．【变式5-1】综合与实践杨老师在黑板上布置了一道题，求代数式：x2―4y2―x2+6xy+9y2+6xy的值．（1）请思考该代数式与哪个字母无关? 知道哪个字母的值就能求出此代数式的值?【变式应用】（2）若多项式3(mx―1)+m2―3x的值与x的取值无关，求m的值．【能力提升】（3）如图1，小长方形的长为a，宽为b．用7张小长方形按照图2所示的方式不重叠地放在大长方形ABCD 内，将大长方形中未被覆盖的两个部分涂上阴影，设右上角阴影部分的面积为S1，左下角阴影部分的面积为S2．当AB的长变化时，a与b满足什么关系，S1―S2的值能始终保持不变?【变式5-1】（1）若关于x 的多项式m (2x ―3)+2m 2―4x 的值与x 的取值无关，求m 值；（2）已知A =―2x 2―2(2x +1)―x (1―3m )+x ，B =―x 2―mx +1，且A ―2B 的值与x 的取值无关，求m 的值；（3）7张如图1的小长方形，长为a ，宽为b ，按照图2方式不重叠地放在大长方形ABCD 内，大长方形中未被覆盖的两个部分都是长方形．设右上角的面积为S 1，左下角的面积为S 2，当AB 的长变化时，S 1―S 2的值始终保持不变，求a 与b 的等量关系．【题型6 化简求值】【典例6】已知代数式A =6x 2+3xy +2y ，B =3x 2―2xy +5x ．(1)求A ―2B ；(2)当x =1，y =2时，求A ―2B 的值．【变式6-1】先化简再求值(1)―mn 2+(3m 2n ―mn 2)―2(2m 2n ―mn 2)，其中m =―2，n =―1．(2)2(x 2y +xy 2)―32(43xy 2+23x 2y ―23)―2，其中(4y +x)2+|x +2|=0．【变式6-2】化简求值：2a 2b ―ab 2―2(2a 2b ―ab 2)―ab 2，其中|a ―1|+|b +3|=0．(1)求a ，b 的值(2)化简并求出代数式的值．【变式6-3】先化简，再求值：4xy ―x 2―2y 2+3x 2―2xy ，（其中x =2，y =1）【变式6-4】已知A =3x 2―4x ，B =x 2+x ―2y 2(1)当x =―2时，试求出A 的值；(2)当x =12，y =13时，请求出A ―3B 的值．【题型7 绝对值化简求值】【典例7】有理数a 、b 、c 在数轴上表示如图所示：(1)填空：|a|=_______，|b|=_______，|c |=_______(2)化简|a +b|―|b ―c|+|b +c|；【变式7-1】有理数a，b，c，在数轴上位置如图：(1)c―a______0；a+b______0；b―c______0．(2)化简：|c―a|―|a+b|+|b―c|．【变式7-2】如图，数轴上的点A，B，C分别表示有理数a，b，c．(1)比较大小：a 0，b ―2（填“>”、“ <”或“=” )；(2)化简：|a|―|b+2|―|a+c|．【题型8 非负性求值】【典例8】如果，|a―2|+(b+1)2=0，则(a+b)2015的值为（）A．1B．2C．3D．―1【变式8-1】已知|x―3|+(y+2)2=0则xy的值为（）A．6B．―6C．5D．―5【变式8-2】若|y―2024|+|x+2023|=0，则x+y的值是（）A．―1B．1C．0D．2【题型9 定义求值】【典例9】对于有理数a、b，定义一种新运算：a⊗b=ab+|a|―b(1)计算5⊗4的值(2)若m是最大的负整数，n的绝对值是3，计算m⊗n【变式9-1】用“⊙”定义一种新运算：规定a ⊙b =ab 2―a ，例如：1⊙2=1×22―1=3．(1)求(―8)⊙(―2)的值；(2)化简：(2m ―5n )⊙(―3)．【变式9-2】定义：对于任意相邻负整数a ，b ，规定：a △b =1ab ．(1)理解定义：例：(―1)△(―2)=1(―1)×(―2)=12；练习：(―2)△(―3)=；(2)探究规律：某数学兴趣小组发现：可将a △b 转换为减法．你发现了吗？是什么？（温馨提示：你可再举几个例子试试，然后用含a 与b 的代数式将a △b 转换为减法．）(3)应用规律：运用发现的规律求(―1)△(―2)+(―2)△(―3)+(―3)△(―4)+⋯+(―2023)△(―2024)的值．【变式9-3】给出定义如下：我们称使等式a ―b =ab +1的成立的一对有理数a ，b 为“共生有理数对”，记为(a ,b )，如：2―13=2×13+1,5―23=5×23+1，那么数对 2,5,“共生有理数对” ．(1)判断，正确的打“√”，错误的打“×”． ①数对(―2,1)是“共生有理数对”；（ ）②数对3,“共生有理数对” ．（ ）(2)请再写出一对符合条件的“共生有理数对”： ；（注意：不能与题目中已有的“共生有理数对”重复）(3)若(m ,n )是“共生有理数对”，则(―n,―m )是不是“共生有理数对”？ 并说明理由．(4)若(a ,3)是“共生有理数对”，求a 的值．。

2023年中考数学高频考点训练——利用分式运算化简求值一、解答题1．先化简，再求代数式23211224a a a a -+⎛⎫-÷ ⎪++⎝⎭的值，其中2cos 4530a =︒+︒．2．先化简，再求值：2221111x x x x x ++⎛⎫-÷ ⎪--⎝⎭，其中1x =.3．先化简，再求值：223244142x x xx x x ⎛⎫++-÷ ⎪--⎝⎭，其中0x <<，且x 是整数．4．先化简，再求值：22211391x x xx x x x+÷-⋅--+，其中x ＝2．5．先化简，再求值：22()ab b a b a a a--÷-，其中a ，b 满足23(2)a b -+-=0．6．先化简，再求值2111211x x x x x x +⎛⎫+÷⎪--+-⎝⎭，其中1x =.7．先化简：（21a a +﹣a+1）÷21a a -，然后将﹣1，0，12中，所有你认为合适的数作为a 的值，代入求值.8．先化简，再求值：，从0，-1，1，中选择一个适当的数作为x 值代入.9．先化简，再求代数式35222a a a a -⎛⎫÷-- ⎪++⎝⎭的值．其中a ＝2sin60°﹣3tan45°．10．已知2340m m +-=，求代数式253(2)22m m m m m-+-÷--的值.11．已知代数式T =（b a -a b ）÷a b b+.若点A （a ，b ）在直线y=3x 上，求T 的值.12．先化简，后求值2211121a a a a a -⎛⎫-÷ ⎪+++⎝⎭，其中1a =.13．先化简，再求值：113263x x x x x +-⎛⎫÷- ⎪--⎝⎭，其中3045x cos tan =︒+︒．14．先化简，再求值：23222(22x x y y x y x xy y --÷+++，其中x ＝3，y ＝2．15．化简2231422a a a a a a-÷--+-，并求值，其中a 与2，3构成△ABC 的三边，且a 为整数．16．2222444424x x x x x x x ⎛⎫---÷ ⎪-+--⎝⎭先化简，再从234、、中选一个合适的数作为x 的值代入求值．17．化简22442224a a a a a a ⎛⎫+-+⨯ ⎪---⎝⎭，并从1，2，3中选取所有合适的数作为a 代入求值.18．先化简，再求值：（31a +﹣a+1）÷2441a a a -+++42a -﹣a ，并从﹣1，0，2中选一个合适的数作为a 的值代入求值.19．求代数式222232x y x x y y x ++--的值，其中2x y =+.20．先化简，再求值：221211y x y x y y x⎛⎫-÷ ⎪-+-⎝⎭，其中2022x y =+．21．先化简，再求值21121111a a a a a a +++-÷---，在-1，0，1，2四个数中选一个合适的代入求值．22．当2(1)0x -+=时，求代数式22112x y x y x y x xy y x y-+-÷-+++-的值．答案解析部分1．【答案】解：原式()()21322222a a a a a -+⎛⎫=-÷⎪+++⎝⎭()()2132222a a a a ---=÷++()()222121a a a a +-=-⋅+-21a =--．当2cos 4530a =︒+︒23223=⨯+1=时原式==．【解析】【分析】先化简分式，再将a 代入计算求解即可。

2023年中考数学高频考点训练——整式的混合运算一、解答题1．先化简，再求值：（x+1）（x ﹣1）+x 2（1﹣x ）+x 3，其中x=22．已知3x 2＋2x ﹣5＝0，求代数式（2x ＋1）（2x ﹣1）﹣x （x ﹣2）的值．3．定义新运算“※”：x※y=xy+x 2﹣y 2，化简（2a+3b ）※（2a ﹣3b ），并求出当a=2，b=1时的值． 4．去括号，并合并相同的项：x ﹣2（x+1）+3x5．先化简，再求值：（2+a ）（2﹣a ）+a （a ﹣5b ）+3a 5b 3÷（﹣a 2b ）2，其中ab=﹣12． 6．已知（m-x ）·（-x ）+n （x+m ）=x 2+5x-6对于任意x 都成立，求m （n-1）+n （m+1）的值。

7．某中学一寝室前有一块长为32x ，宽为x 的空地，学校向全校师生征集这块地的绿化设计方案并要求绿地面积不少于58x 2，如图是学生小明的设计方案，阴影部分是绿地．试问小明的设计方案是否合乎要求？为什么？8．先去括号，在合并同类项：3（2x 2﹣y 2）﹣2（3y 2﹣2x 2）9．如图，某村在建设社会主义新农村中，开展了“美丽乡村”建设，现准备在一块长为（3x+y ）米，宽为（2x+y ）米的长方形土地上，划出一块边长为（x+y ）米的正方形建设村民活动中心，为村民休闲健身提供去处，并将图中的阴影部分进行绿化，问：绿化面积是多少平方米？并求出当x ＝5，y ＝4时的绿化面积.10．已知多项式A 和B ， ()()251323A m x n xy x y =+++-+ ， 26521B x xy x =+-- ，当A与B 的差不含二次项时，求：(-1)m+n ()3mm n n ⎡⎤⋅-+--⎣⎦的值．11．已知x 2﹣4x ﹣1=0，求代数式（2x ﹣3）2﹣（x+y ）（x ﹣y ）﹣y 2的值．12．先化简，再求值：[（xy+2）（xy ﹣2）﹣2（x 2y 2﹣2）]÷（xy ），其中x=10，y=﹣ 125． 13．化简:（1）(-2ab )(3a 2-2ab -4b 2); （2）3x (2x -3y )-(2x -5y )·4x .14．如图，在边长为（2m+3）的正方形纸片中剪出一个边长为（m+3）的正方形之后，剩余部分可剪拼成一个长方形，若拼成的长方形一边长为m ，求另一边长．15．先化简，再求值：（a+2b ）（a ﹣2b ）﹣（a ﹣2b ）2，其中a=﹣13，b=﹣3． 16．Peter 从批发市场以每个m 元的价格购进100个手机充电宝，然后每个加价n 元后出售.（1）求售出100个手机充电宝的总售价为多少元?（2）若他售出60个充电宝后，将剩余充电宝按售价8折出售，相比不采取降价销售，他将比实际销售多盈利多少元?17．已知A=（x ﹣3）2，B=（x+2）（x ﹣2）（1）化简多项式2A ﹣B ； （2）若2A ﹣B=2，求x 的值．18．已知一个多项式除以a 2﹣3a+1得到商式是2a+1，求这个多项式． 19．计算题（1）（﹣3a 4）2﹣a•a 3•a 4﹣a 10÷a 2 （2）（x+2）2﹣（x ﹣1）（x ﹣2） （3）1982（4）[（x+y ）2﹣（x ﹣y ）2]÷（2xy ）20．已知） 1xy + 与 ()25x - 互为相反数，求代数式 2222253333x y xy xy x y xy xy ⎡⎤⎛⎫---++ ⎪⎢⎥⎝⎭⎣⎦的值.21．5a －{－3b ＋[6c －2a －(a －c)]}－[9a －(7b ＋c)] 22．试证明：任何五个相邻的整数的平方和不是平方数．答案解析部分1．【答案】【解答】解：原式=x2﹣1+x2﹣x3+x3=2x2﹣1；当x=2时，原式=2×22﹣1=7．【解析】【分析】根据乘法公式和单项式乘以多项式法则先化简，再代入求值即可．2．【答案】解：（2x+1）（2x-1）-x（x-2）=4x2-1-x2+2x=3x2+2x-1，当3x2+2x-5=0时，原式=（3x2+2x-5）+4=0+4=4．【解析】【分析】先利用整式的混合运算化简，再将3x2＋2x﹣5＝0整体代入计算即可。

整式的化简求值的五种类型（原卷版）【专题精讲】整式的化简常与求值相结合,体现了特殊与一般的辩证关系.解决这类问题的大体步骤可以简化为“一化、二代、三计算”,但有时也可根据题目的特征和已知条件灵活选择解题方法.根据代入方法的不同,可将整式的化简求值题划分为以下几种类型：(1)利用直接代入法求值;(2)利用整体代入法求值(3)利用拆项或添项法求值(4)利用降次消元法求值;(5)利用赋值法求值◎类型一：利用直接代入法求值解题方法：整式的化简求值一般分为三步：一是利用整式加减的运算法则将整式化简;二是把已知字母或某个整式的值代入化简后的式子;三是依据有理数的运算法则进行计算1．（黑龙江省大庆市庆新中学2021-2022学年六年级（五四学制）下学期期末考试数学试题）先化简再求值213()(1)322----+xy y xy x其中54,33x y==2．（2022·湖南·长沙市开福区清水塘实验学校七年级期末）先化简再求值：()()23343334a a a a a+----+其中a＝﹣1．3．（2020·天津市红桥区教师发展中心七年级期中）已知2223A x xy y=+-2223B x xy y=-+(1)求32A B +；(2)当21，==x y 求32A B +的值.4．（2021·福建·福州十八中七年级期中）先化简 再求值：(1)()()2232223,a a a a ---其中3a =-．(2)()2272421,x y xy xy x y ⎡⎤-----+⎣⎦其中x y 满足()2201510x y -++=．◎类型二：利用整体代入法求值解题方法：解答此类题目,先将原式化简,再将已知条件(或变形后的条件)整体代入求值。

5．（2022·全国·七年级单元测试）已知3,2a b c d +=-= 则()()a c b d +--+的值是（ ） A ．5 B ．-5 C ．1 D ．-16．（2021·福建漳州·七年级期中）若代数式13-22x y = 则代数式2()22421x y y x -+-+的值为（ ）A ．7B ．13C ．19D ．257．（2022·全国·七年级课时练习）已知21x y -= 则式子22(43)(2)y x y y ----的值为（ ） A ．-1 B ．1 C ．-5 D ．58．（2022·全国·七年级课时练习）若21a a += 则代数式2225+-a a 的值为（ ） A ．0 B ．1 C ．2 D ．3-◎类型三：无关类题型的求值9．（2020·天津市红桥区教师发展中心七年级期中）已知2232A a b ab abc =-+ 小明错将“2A B -”看成“2A B +”,算得结果22434C a b ab abc =-+.(1)计算B 的表达式；(2)求正确的结果的表达式；(3)小强说（2）中的结果的大小与c 的取值无关 对吗？若1185a b ==，求（2）中代数式的值10．（2021·陕西·西北大学附中七年级期中）如果关于x 、y 的代数式()()22262351x ax y bx x y +-+--+-的值与字母x 所取的值无关 试化简代数式323212234a b a b ⎛⎫--- ⎪⎝⎭再求值．11．（2022·全国·七年级专题练习）已知多项式M ＝()()2223221x xy y x x yx -+++++． (1)当x ＝1 y ＝2 求M 的值；(2)若多项式M 与字母x 的取值无关 求y 的值．12．（2022·全国·七年级专题练习）已知代数式22212,221A x xy y B x xy x =++-=-+-．(1)当x ＝﹣1 y ＝﹣2时 求2A ﹣B 的值．(2)若2A ﹣B 的值与x 的取值无关 求y 的值．◎类型四：图形类问题的应用求值13．（2022·浙江绍兴·七年级期末）已知有2个完全相同的边长为a 、b 的小长方形和1个边长为m 、n 的大长方形 小明把这2个小长方形按如图所示放置在大长方形中 小明经过推事得知 要求出图中阴影部分的周长之和 只需知道a 、b 、m 、n 中的一个量即可 则要知道的那个量是（ ）A ．aB ．bC ．mD ．n14．（2022·浙江宁波·七年级期末）如图所示 三张正方形纸片① ① ①分别放置于长()a b + 宽()a c +的长方形中 正方形① ① ①的边长分别为a b c 且a b c >> 则阴影部分周长为（ ）A ．42a c +B ．42a b +C ．4aD ．422a b c ++ 15．（2021·广东·揭西县宝塔实验学校七年级期中）如图 大长方形ABCD 是由一张周长为C 1正方形纸片①和四张周长分别为C 2 C 3 C 4 C 5的长方形纸片① ① ① ①拼成 若大长方形周长为定值 则下列各式中为定值的是（ ）A ．C 1B ．C 3+C 5 C ．C 1+C 3+C 5D ．C 1+C 2+C 416．（2022·山东·万杰朝阳学校期中）如图 阴影部分的面积是 ( )A ．72xyB ．92xyC ．4xyD ．2xy◎类型五：利用数轴化简求值17．（2022·全国·七年级课时练习）已知A B C 三点在数轴上如图所示 它们表示的数分别是a b c ．且|a |＜|b |．(1)填空：abc 0 a +b 0（填“＞”“＜”或“＝”）．(2)化简：|a ﹣b |﹣2|a +b |+|b ﹣c |．18．（2022·贵州黔西·七年级期末）（1）已知有理数a b c 在数轴上的对应点的位置如图所示 化简：a b c b b a +--+-；（2）若x 的相反数是2- y 没有倒数 24z = 求2()x y z x y z -++-+-的值．19．（2021·河南开封·七年级期中）已知x 、y 两数在数轴上表示如图．（1）试在数轴上找出表示x - y -的点 并用“<”连接x y x - y -．（2）若x 的绝对值等于3 y 的倒数等于它本身 化简求值：32x y y x -+-．20．（2021·天津·耀华中学七年级期中）已知在数轴上的位置如图所示：（1）判断下列式子正负：a +1 0；c ﹣b 0；b ﹣1 0；（2）化简：|a +1|+|c ﹣b |﹣|b ﹣1|；（3）若332b x y -与123a a x y --的差仍是单项式 且a 与﹣1的距离等于c 与﹣1的距离 求﹣4c 2+2（a ﹣4b ）﹣3（﹣c 2+5a ﹣b ）的值．【专题训练】1．（2022·广西贵港·七年级期末）若a ﹣5＝6b 则(a +2b )﹣2(a ﹣2b )的值为（ ） A ．5 B ．﹣5 C ．10 D ．﹣102．（2022·全国·七年级课时练习）如果a ﹣4b ＝0 那么多项式2（b ﹣2a +10）+7（a ﹣2b ﹣3）的值是（ ）A ．﹣1B ．﹣2C ．1D ．23．（2021·黑龙江·绥芬河市第三中学七年级期中）把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m 宽为n )的盒子底部(如图①) 盒子底面未被卡片覆盖的部分用阴影表示 则图①中两块阴影部分的周长和是( )A ．4mB ．4nC ．2(m ＋n )D ．4(m －n ) 4．（2022·浙江绍兴·七年级期中）如图 大长方形按如图方式分成5块 其中标号① ① ①的为正方形 标号① ①的为长方形 若要求出①与①的周长差 则只需知道下列哪个条件（ ）A ．①的周长B ．①的周长C ．①的面积D ．①的面积 5．（2020·湖北·公安县教学研究中心七年级期中）先化简 再求值：()()222221653242ab a b ab ab a b +-+-- 其中a ＝2、b ＝-12． 6．（2021·河北·原竞秀学校七年级期中）老师在黑板上书写了一个正确的演算过程 随后用一张纸挡住了一个多项式 形式如下：()2231251x x x +-=--+(1)求所挡的多项式；(2)当1x =-时 求代数式的值．7．（2022·全国·七年级专题练习）已知代数式22232A x xy y B x xy x ＝＋＋，＝﹣＋． (1)求A ﹣2B ；(2)当x ＝﹣1 y ＝3时 求A ﹣2B 的值；(3)若A ﹣2B 的值与x 的取值无关 求y 的值．8．（2020·浙江·余姚市姚江中学七年级期中）已知：222351 2.A x xy x B x xy =+-+=-++，(1)当2,1x y =-=时 求2A B +的值．(2)若2A B +的值与x 的值无关 求y 的值．9．（2021·重庆市万州第二高级中学七年级阶段练习）（1）已知325A x x =- 2116B x x =-+ 求当1x =时 求()3A A B ---+⎡⎤⎣⎦；（2）已知||5a = ||8b = 且0a b +> 求ab 的值；（3）已知有理数,,a b c 在数轴上对应的点如图所示：化简：|||2|||b a a c c b --+-+= ．10．（2020·山东·日照市新营中学七年级期中）条件求值：（1）对于有理数a 、b 定义运算：a ①b ＝a ×b ＋|a |－b ．计算(－5)①4的值；（2）已知有理数a b c 在数轴上对应点的位置如图所示 化简：|b －c |＋2|c ＋a |－3|a －b |；（3）若代数式x 2的值和代数式2x ＋y －1的值相等 则代数式9－2(y ＋2x )＋2x 2的值；y＝2．（4）先化简再求值：3x2y－[2x2y－3(2xy－x2y)－xy] 其中x＝12。

2023年中考数学高频考点训练——利用整式的混合运算化简求值一、解答题1．先化简，再求值()()()()222252x y x y x y y x ⎡⎤++++-÷⎣⎦，其中 x ， y 满足 ()2230x y -+-= .2．先化简，再求值()()()()222352x y x y x y y x ⎡⎤+-+--÷-⎣⎦ ，其中 14,4x y =-= ． 3．先化简，再求值． 2(32)(32)7(1)2(1)x x x x x +----- ，其中 3x = ． 4．化简求值：x－(5x －4y)＋3(x －y)，其中x=－1，y=2．5．先化简，再求值()23(2)(2)x x x x --+-，其中1x =- 6．已知：|a +6|＋(b ＋12 )2＝0，求：5a 2b －[2ab 2－2(ab － 52a 2b )＋ab ]＋5ab 2的值． 7．先化简，再求值：()()22(2)211x x x x x +⋅-+-+，其中12x =． 8．先化简，再求值：()()22221132542a a a aaa ⎡⎤-----⎣⎦，其中4a =-．9．先化简，再求值：[（x ﹣2y ）2﹣（2x ﹣y ）（2x ＋y ）＋x （3x ﹣2y ）]÷2y ，其中x ＝13，y ＝﹣2 10．先化简，再求值：()()()5232b a b a b a a b a b a b+--++÷+﹐其中a=-8，b=2.11．先化简，再求值：[（a ﹣b ）2+（2a+b ）（1﹣b ）﹣b]÷（﹣12a ），其中a 、b 满足（a+1）2+|2b ﹣1|＝0.12．先化简，再求值（1）()()221x x x -++ ，其中 1x = .（2）()()22x y x y ++- ()()5x y x x y +-- ，其中 21x = ， 21y =.13．先化简，再求值()()()222a b a b a b a +++--，其2a =，12b =-． 14．先化简，再求值：2(2)(2)()a b a b a b ++-+，其中12a b ==-，．15．已知2220x x +-=，求代数式2(2)(1)x x x +++的值． 16．已知()()322x mx nxx +++-展开式中不含3x 和2x 项，求代数式()22()m n m mn n -++的值.17．先化简，再求值：（2x ﹣1）2+（x+6）（x ﹣2），其中x ＝2． 18．先化简再求值： ()()()222222131a b aba b ab+--+- ，其中 12a =， 2b =- ．19．先化简，再求值：22224(2)2(3)a b ab ab a b --+，其中a ，b 满足3214 6.a b a b +=⎧⎨-=-⎩，20．（1）解方程： 8753x x +=-（2）先化简，再求值： 2222(32)2(2)a b ab ab a b --- ，其中 2a = , 1b =-21．已知 22231x y += ，求代数式 ()25244x y y x y ⎛⎫+-- ⎪⎝⎭的值． 22．先化简，再求值：()()()2232323343434x y xy x y ------，其中x ，y 满足12x +与2(1)y -互为相反数.答案解析部分1．【答案】解： ()()()()222252x y x y x y y x ⎡⎤++++-÷⎣⎦()22222442252x xy y x xy xy y y x =++++++-÷ ()2372x xy x =+÷3722x y =+ ()2230x y -+-=20,30x y ∴-=-= 2,3x y ∴==将 2,3x y == 代入原式，得3721272332222⨯+⨯=+= 【解析】【分析】利用整式的运算法则进行化简，之后代入值进行求解即可. 2．【答案】原式 ()()22222443352x xy y x xy xy yyx ⎡⎤=++--+--÷-⎣⎦22222(44335)(2)x xy y x xy xy y y x =++-+-+-÷- 2(22)(2)x xy x =-+÷-x y =-将 14,4x y =-=代入得：原式 117444x y =-=--=- ． 【解析】【分析】先利用完全平方公式进行计算、多项式的乘法，再计算整式的加减法与除法，然后将x 、y 的值代入求解即可．3．【答案】解：原式 2229477242116x x x x x x =--+-+-=- ，当 3x = 时，原式 27=【解析】【分析】先计算整式的乘法，再合并同类项，代入求值即可． 4．【答案】解： 原式= x 2－5x 2+4y ＋3x 2－3y=-x 2+y ，当 x=－1 ，y=2时， 原式=-1+2=1．【解析】【分析】先利用整式的整式混合运算化简，再将x 、y 的值代入计算即可。

专题02整式化简求值（四大类型）整式的化简求值中,当单个字母的值不易求出或化简后的结果与已知值的式子相关联时,需要将已知式子的值整体代入计算，是考试中必考考点。

【新方法解读】类型一先化简，再直接代入求值类型二先化简，结合几个有理数和为零再代入类型三先化简，再整体代入求值类型四先化简，再利用特殊条件带入求值【典例分析】【典例1】（2022秋•南关区校级期末）先化简，再求值：（x﹣2y）2﹣（x+y）（x﹣y）﹣5y2，其中x＝，y＝﹣3．【变式1-1】（2022秋•西峡县期末）先化简，再求值：，其中x＝．【变式1-2】（2022秋•二道区校级期末）先化简，再求值：（a+1）2﹣（a+3）（a﹣3），其中．【变式1-3】（2022秋•二道区校级期末）先化简，再求值：（a+1）2﹣（a+2）（a﹣2），其中．【典例2】（2022秋•沙坪坝区校级期末）先化简，再求值：﹣8m2n+（m﹣n）（2m+n）﹣2mn（﹣3m+4n）+8mn2，其中（m+2）2+|n﹣|＝0【变式2-1】（2022春•靖江市校级月考）先化简，再求值：，其中．【变式2-2】（2022春•江都区期中）先化简，再求值：[（x+2y）（x﹣2y）+4（x﹣y）2]÷（﹣x），其中|x+2|+（y﹣1）2＝0．【典例3】（2022春•明溪县月考）已知x2﹣4x+1＝4，求代数式4x（x﹣3）﹣（x+y）（x﹣y）﹣y2的值．【变式3-1】（2022春•东昌府区校级月考）已知x2+x﹣2022＝0，将下式先化简，再求值：（2x+3）（2x﹣3）﹣x（5x+4）﹣（x﹣1）2．【变式3-2】（2022秋•卧龙区校级期末）已知a2﹣2a﹣1＝0，求代数式（2a+1）（2a﹣1）+（a﹣5）2的值．【典例4】（2021春•武侯区期末）（1）先化简，再求值：[（2x﹣y）2﹣（x﹣y）（x+y）﹣2y2]÷x，其中x＝2，y＝﹣3；（2）已知a为常数，关于x的代数式（x2﹣3x+2）（x2+ax）的化简结果中不含x3项，且（m﹣2）2+|n﹣3|＝0，求a m﹣n的值【变式4-1】（2022秋•鲤城区校级期中）已知关于x、y的代数式（2x+5y3）（2x﹣5y3）﹣（mx﹣3）2+nx的值与x的取值无关，求实数m、n的值．【变式4-2】（2021秋•邓州市期末）（1）先化简再求值：a2﹣3（2a+3）+6a+1，其中a＝﹣1．（2）小亮在对代数式2x2+ax﹣y+6﹣2bx2+4x﹣6y+3进行化简后，发现化简的结果与字母x的取值无关，请求出代数式（a﹣b）2的值．【夯实基础】1．（2022春•新城区校级月考）若x2+x﹣2＝0．那么代数式（x﹣6）（x+3）﹣2x（x﹣1）的值为（）A．40B．4C．﹣18D．﹣20 2．（2022秋•兰考县月考）如果m2﹣2m﹣3＝0，那么代数式（m+3）（m﹣3）+（m﹣2）2的值为（）A．0B．﹣1C．1D．3 3．（2022春•沙坪坝区校级期中）如果m2﹣2m﹣4＝0，那么代数式（m+3）（m ﹣3）+（m﹣2）2的值为（）A．﹣3B．﹣1C．1D．3 4．（2021秋•潜江期末）如果m2﹣m＝2，那么代数式m（m+2）+（m﹣2）2的值为（）A．﹣8B．﹣6C．6D．8 5．（2022秋•北京期末）已知5m2+4m﹣1＝0，则代数式（2m+1）2+（m+3）（m﹣3）的值为．6．（2022春•高州市期中）化简：（x﹣y）2+（x+y）（x﹣y）﹣5x（x﹣y）．（1）若x是任意整数，请观察化简后的结果，它能被3整除吗？（2）当（x+1）2+|y﹣2|＝0时，求代数式的值．7．（2022春•鼓楼区期末）先化简，再求值：（x﹣y）2﹣（2x+y）（2x﹣y）+3x （x+y），其中|x+3|+（y﹣2）2＝0．8．（2022秋•北京期末）已知：x2﹣2x﹣2＝0，求代数式的（2x﹣1）2﹣（x﹣1）（x+3）值．9．（2022秋•安顺期末）先化简，再求值已知代数式（ax﹣3）（2x+4）﹣x2﹣b化简后，不含有x2项和常数项．（1）求a、b的值；（2）求（b﹣a）（﹣a﹣b）+（﹣a﹣b）2﹣a（2a+b）的值．10．（2019秋•锡山区期中）若代数式（2x2+ax﹣y+6）﹣（2bx2﹣3x+5y﹣1）的值与字母x的取值无关，求代数式的值．11．（2021春•招远市期中）（1）先化简，再求值：（2x+y）2﹣（x+2y）（x ﹣2y）﹣（3x﹣y）（x﹣5y），其中x＝﹣3，y＝．（2）说明代数式[（x﹣y）2﹣（x+y）（x﹣y）]÷（﹣2y）+y的值，与y的值无关．专题02整式化简求值（四大类型）整式的化简求值中,当单个字母的值不易求出或化简后的结果与已知值的式子相关联时,需要将已知式子的值整体代入计算，是考试中必考考点。