高中数学课后巩固作业6新人教A版必修3

[A基础达标]1．在“世界读书日”前夕，为了了解某地5 000名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析，在这个问题中，5 000名居民的阅读时间的全体是()A．总体B．个体C．样本的容量D．从总体中抽取的一个样本解析：选A.根据题意，结合总体、样本、个体、样本容量的定义可知，5 000名居民的阅读时间的全体是总体．2．从52名学生中选取5名学生参加全国“希望杯”数学竞赛，若采用简单随机抽样抽取，则每人入选的可能性()A．都相等，且为1 52B．都相等，且为110C．都相等，且为552 D．都不相等解析：选C.根据随机抽样的等可能性可知，每人入选的可能性都相等，且为552，应选C.3．下面抽样方法是简单随机抽样的是()A．从平面直角坐标系中抽取5个点作为样本B．可口可乐公司从仓库中的1 000箱可乐中一次性抽取20箱进行质量检查C．某连队从200名战士中，挑选出50名最优秀的战士去参加抢险救灾活动D．从10个手机中逐个不放回地随机抽取2个进行质量检验(假设10个手机已编好号，对编号随机抽取)解析：选D.A中平面直角坐标系中有无数个点，这与要求总体中的个体数有限不相符，故错误；B中一次性抽取不符合简单随机抽样逐个抽取的特点，故错误；C中挑选50名最优秀的战士，不符合简单随机抽样的等可能性，故错误．4．已知总体的个数为111，若用随机数表法抽取一个容量为12的样本，则下列对总体的编号正确的是()A．1，2，…，111B．0，1，…，111C．000，001，…，111D．001，002，…，111解析：选D.在使用随机数表法抽取样本时，必须保证编号的位数一致，同时要规范编号，不能多也不能少，结合所给选项，选D.5．为了了解参加运动会的2 000名运动员的年龄情况，从中抽取20名运动员的年龄进行统计分析．就这个问题，下列说法中正确的为()①2 000名运动员是总体；②每个运动员是个体；③所抽取的20名运动员是一个样本；④样本容量为20；⑤每个运动员被抽到的机会相等．A ．①⑤B ．④⑤C ．③④⑤D ．①②③解析：选B.①2 000名运动员不是总体，2 000名运动员的年龄才是总体；②每个运动员的年龄是个体；③20名运动员的年龄是一个样本．6．下列调查的样本合理的是________．①在校内发出一千张印有全校各班级的选票，要求被调查学生在其中一个班级旁画“√”，以了解最受欢迎的教师是谁；②从一万多名工人中，经过选举，确定100名代表，然后投票表决，了解工人们对厂长的信任情况；③到老年公寓进行调查，了解全市老年人的健康状况；④为了了解全班同学每天的睡眠时间，在每个小组中各随机抽取3名学生进行调查． 解析：①中样本不具有代表性、有效性，在班级前画“√”与了解最受欢迎的老师没有关系；③中样本缺乏代表性；而②④是合理的样本．答案：②④7．用随机数表法从100名学生(男生25人)中抽选20人进行评教，某男学生被抽到的机率是________．解析：简单随机抽样是等可能性抽样，每个个体被抽到的机率都是20100＝15. 答案：158．齐鲁风采“七乐彩”的中奖号码是从分别标有1，2，…，30的三十个小球中逐个不放回地摇出7个小球来按规则确定中奖情况，这种从30个号码中选7个号码的抽样方法是________．解析：三十个小球相当于号签，搅拌均匀后逐个不放回地抽取，这是典型的抽签法． 答案：抽签法9．某校2018级高一年级有50位任课教师，为了调查老师的业余兴趣情况打算抽取一个容量为5的样本，问此样本若采用抽签法将如何获得？解：首先，把50位任课教师编上号码：1，2，3，…，50.制作50个形状、大小均相同的号签(号签可以用小球、卡片、纸条等制作)，然后将这些号签放在一个不透明的箱子里，进行均匀搅拌．抽签时，每次从中抽出1个号签，不放回，连续抽取5次，就得到一个容量为5的样本．10．现有一批编号为10，11，…，99，100，…，600的元件，打算从中抽取一个容量为6的样本进行质量检验．如何用随机数表法设计抽样方案？解：(1)将元件的编号调整为010，011，012，...，099，100， (600)(2)在随机数表中任选一数作为开始数字，任选一方向作为读数方向．比如，选第6行第7列的数“9”，向右读(见课本随机数表)．(3)每次读取三位，凡不在010～600中的数跳过去不读，前面已经读过的也跳过去不读，依次可得到544，354，378，520，384，263.(4)以上号码对应的6个元件就是要抽取的样本．[B 能力提升]11．从一群玩游戏的小孩中随机抽出k 人，一人分一个苹果，让他们返回继续游戏．过了一会儿，再从中任取m 人，发现其中有n 个小孩曾分过苹果，估计参加游戏的小孩的人数为( )A.kn mB ．k ＋m －n C.km nD ．不能估计 解析：选C.设参加游戏的小孩有x 人，则k x ＝n m ，x ＝km n. 12．从个体数为N 的总体中抽出一个样本容量是20的样本，每个个体被抽到的可能性是15，则N 的值是________． 解析：从个体数为N 的总体中抽出一个样本容量是20的样本，所以每个个体被抽取的可能性是20N .因为每个个体被抽取的可能性是15，所以20N ＝15，所以N ＝100. 答案：10013．某班共有60名学生，现领到10张听取学术报告的入场券，用抽签法和随机数表法把10张入场券分发下去，试写出过程．解：(1)抽签法：①先将60名学生编号为1，2， (60)②把号码写在形状、大小均相同的号签上；③将这些号签放在同一个箱子里进行均匀搅拌，抽签时每次从中抽出一个号签，连续抽取10次，根据抽到的10个号码对应10名同学，10张入场券就分发给了10名同学．(2)随机数表法：①先将60名学生编号，如编号为01，02， (60)②在随机数表中任选一个数作为开始，从选定的数可向任意方向读，如果读到的数小于或等于60，将它取出，如果读到的数大于60，则舍去，前面已读过的也舍去，直到已取满10个小于或等于60的数为止，说明10个样本号码已取满．③根据号码对应的编号，再对应抽出10名同学，10张入场券就分发给了10名被抽到的同学．14．(选做题)某电视台举行颁奖典礼，邀请20名港台、内地艺人演出，其中从30名内地艺人中随机选出10人，从18名香港艺人中随机挑选6人，从10名台湾艺人中随机挑选4人．试用抽签法确定选中的艺人，并确定他们的表演顺序．解：第一步：先确定艺人：(1)将30名内地艺人从1到30编号，然后用相同的纸条做成30个号签，在每个号签上写上这些编号，然后放入一个不透明的箱子中摇匀，从中抽出10个号签，则相应编号的艺人参加演出．(2)运用相同的办法分别从10名台湾艺人中抽取4人，从18名香港艺人中抽取6人．第二步：确定演出顺序：确定了演出人员后，再用相同的纸条做成20个号签，上面写上1到20这20个数字，代表演出的顺序，让每个演员抽一张，每人抽到的号签上的数字就是这位演员的演出顺序，再汇总即可．。

章末复习课课时目标 1.进一步巩固和理解本章重要知识点.2.学会用算法的思想处理问题．1．下列关于算法的说法正确的有( ) ①求解某一类问题的算法是唯一的； ②算法必须在有限步操作之后停止；③算法的每一步操作必须是明确的，不能有歧义； ④算法执行后一定产生明确的结果．A ．1个B ．2个C ．3个D ．4个2．下图的程序语句输出的结果S 为( ) I ＝1WHILE I<8S ＝2I ＋3I ＝I ＋2WEND PRINT S ENDA ．17B ．19C ．21D ．233．给出以下四个问题，①输入x ，输出它的相反数． ②求面积为6的正方形的周长． ③求三个数a ，b ，c 中的最大数．④求函数f (x )＝⎩⎪⎨⎪⎧x －1， x ≥0x ＋2， x <0的函数值．其中不需要用条件语句来描述其算法的有( )A ．1个B ．2个C ．3个D ．4个4．下边是一个算法的程序框图，当输入的x 值为3时，输出y 的结果恰好是13，则处的关系式是( )A ．y ＝x 3B ．y ＝3－x C ．y ＝3x D ．y ＝x 135．使用秦九韶算法求P (x )＝a n x n ＋a n －1x n －1＋…＋a 1x ＋a 0在x ＝x 0时的值可减少运算次数，做加法和乘法的次数分别是( ) A ．n ，n B ．n ，n (n ＋1)2C ．n,2n ＋1D ．2n ＋1，n (n ＋1)26．三个数72、120、168的最大公约数是________．一、选择题1．如果执行下面的程序框图，那么输出的S 等于( )A ．2 450B ．2 500C ．2 550D ．2 6522．判断下列输入、输出语句正确的是( ) (1)输入语句INPUT a ；b ；c. (2)输入语句INPUT x ＝3. (3)输出语句PRINT B ＝4. (4)输出语句PRINT 20,3*2. A. （1）、（2） B .(2)、(3) C ．(3)、(4) D ．(4)3．若“x ＝3*5”与“x=x+1”是某一个程序中先后相邻的两个语句，那么下列说法正确的是（ ）①x=3*5的意思是x=3×5=15，此式与数学中的算术式是一样的； ②“x=3*5”是将数值15赋给x; ③“x=3*5”可以写成“3*5=x ”;④“x=x+1”在执行时赋值号右边x 的值是15，执行后左边x 的值是16. A.①③ B .②④C ．①④D ．①②③④4．算式1 010(2)＋10(2)的值是( )A．1 011(2)B．1 100(2)C．1 101(2)D．1 000(2)5．程序：INPUT xIF9<x BND x<100THENa＝x\10b＝x MOD 10x＝10]上述程序如果输入的值是51，则运行结果是()A．51 B．15 C．105 D．501)6．如图所示，程序的输出结果为S＝132，则判断框中应填(二、填空题7．将十进制数100转换成二进制数所得结果为______________．8．下边程序运行后，输出的值为________．S＝1i＝1WHILE i<＝5S＝S*ii＝i＋1WENDPRINT SEND9．用辗转相除法求333与24的最大公约数时的循环次数为________．三、解答题10．画出求12－22＋32－42＋…＋992－1002的值的程序框图．11．已知函数y ＝⎩⎪⎨⎪⎧2x 2－1 (x >0)2x ＋1 (x ＝0)－2x 2＋4 (x <0)，试编写程序，输入x 的值后输出y 的值．能力提升12．用秦九韶算法求多项式f(x)＝x 6＋2x 5＋3x 4＋4x 3＋5x 2＋6x 当x ＝2时的值．13．某电信部门规定，拨打市内电话时，如果通话时间不超过3分钟，则收取通话费0.2元；如果通话时间超过3分钟，则超过部分按每分钟0.1元收取通话费(通话不足1分钟时按1分钟计)．试设计一个计算通话费用的算法，画出程序框图，并编写程序．1．算法是对一类问题一般解法的抽象与概括，是把问题的解法划分为若干个可执行的步骤，有时需重复多次，但最终都必须在有限个步骤之内完成，所以在设计算法解决问题时要注意：(1)与解决问题的一般方法相联系，从中提炼出算法． (2)可引入有关的参数和变量对算法步骤加以表达．(3)解决问题的过程可分解为若干个步骤，并能用简洁实用的语言表达． (4)算法过程要便于在计算机上执行．2．程序框图是用规定的图形和指向线来形象、直观、准确的表示算法的图形．设计程序框图时，要先进行算法分析，确定算法的逻辑结构和各步的功能再画程序框图，同时要考虑到编写程序的要求．读、画程序框图是高考在本章中考查的重点．3．基本算法语句有输入语句、输出语句、赋值语句、条件语句和循环语句五种，主要对应顺序结构、条件结构和循环结构．明确各语句的功能和格式，是执行程序的关键，掌握常用的算法对理解程序也很有帮助，用算法语句编写程序时，一般先画程序框图．章末复习课课时目标 1.进一步巩固和理解本章重要知识点.2.学会用算法的思想处理问题．1．下列关于算法的说法正确的有( ) ①求解某一类问题的算法是唯一的； ②算法必须在有限步操作之后停止；③算法的每一步操作必须是明确的，不能有歧义； ④算法执行后一定产生明确的结果．A ．1个B ．2个C ．3个D ．4个 答案 C解析 根据算法的定义有②③④三种说法正确． 2．下图的程序语句输出的结果S 为( ) I ＝1WHILE I<8S ＝2I ＋3I ＝I ＋2WEND PRINT S ENDA ．17B ．19C ．21D ．23 答案 A解析 当I 为7的时候I <8，此时S ＝17， 下一个I 为9时I >8，循环结束，故输出S 为17. 3．给出以下四个问题，①输入x ，输出它的相反数． ②求面积为6的正方形的周长． ③求三个数a ，b ，c 中的最大数．④求函数f (x )＝⎩⎪⎨⎪⎧x －1， x ≥0x ＋2， x <0的函数值．其中不需要用条件语句来描述其算法的有( )A ．1个B ．2个C ．3个D ．4个 答案 A解析 ①、③、④需要用条件语句，②不需用条件语句， 故选A.4．下边是一个算法的程序框图，当输入的x 值为3时，输出y 的结果恰好是13，则处的关系式是( )A ．y ＝x 3B ．y ＝3－x C ．y ＝3x D ．y ＝x 13答案 C解析 当x ＝3时，因为x >0， 所以x ＝x －2，∴x ＝1， 又x ＝1>0，所以x ＝x －2，x ＝－1，x ＝－1时，y ＝13，∴内应填y ＝3x .5．使用秦九韶算法求P (x )＝a n x n ＋a n －1x n －1＋…＋a 1x ＋a 0在x ＝x 0时的值可减少运算次数，做加法和乘法的次数分别是( ) A ．n ，n B ．n ，n (n ＋1)2C ．n,2n ＋1D ．2n ＋1，n (n ＋1)2答案 B6．三个数72、120、168的最大公约数是________． 答案 24解析 三个数中任意两个数的最大公约数与第三个数，求其最大公约数就是这三个数的最大公约数．这三个数的最大公约数为24.一、选择题1．如果执行下面的程序框图，那么输出的S等于()A．2 450 B．2 500 C．2 550 D．2 652答案 C解析本程序框图含有循环结构．第1次循环为k＝1＋1＝21≤50S＝0＋2×1，第2次循环为k＝2＋1＝32≤50S＝2＋2×2，……第50次循环为k＝5150≤50S＝2＋4＋…＋100＝2 550.2．判断下列输入、输出语句正确的是()(1)输入语句INPUT a；b；c.(2)输入语句INPUT x＝3.(3)输出语句PRINT B＝4.(4)输出语句PRINT20,3*2.A. （1）、（2）B.(2)、(3) C．(3)、(4) D．(4)答案D解析(1)错．变量之间应用逗号“，”隔开；(2)错．INPUT语句中只能是变量，而不能是表达式；(3)错．PRINT语句中不能再用赋值号“＝”；(4)对．PRINT语句可以输出常量，表达式的值．3．若“x＝3*5”与“x=x+1”是某一个程序中先后相邻的两个语句，那么下列说法正确的是（）①x=3*5的意思是x=3×5=15，此式与数学中的算术式是一样的；②“x=3*5”是将数值15赋给x;③“x=3*5”可以写成“3*5=x”;④“x=x+1”在执行时赋值号右边x的值是15，执行后左边x的值是16.A.①③B.②④C．①④D．①②③④答案B解析赋值语句有固定的格式，与数学中算术式是不一样的，故①是错误，③也是错误的，根据赋值语句的功用知②④是正确的，故选择B.4．算式1 010(2)＋10(2)的值是()A．1 011(2)B．1 100(2)C．1 101(2)D．1 000(2)答案B解析逢二进一．1 010(2)＋10(2)＝1 100(2)．5．程序：INPUT xIF9<x BND x<100THENa＝x\10b＝x MOD 10x＝10]上述程序如果输入的值是51，则运行结果是()A．51 B．15 C．105 D．501答案 B解析∵x＝51，∴9<x<100，∴a＝51\10＝5，b＝51 MOD 10＝1.∴10*b+a=10×1+5=15.即输出结果为15.6．如图所示，程序的输出结果为S＝132，则判断框中应填()A ．i ≥10?B ．i ≥11?C ．i ≤11?D ．i ≥12? 答案 B解析 对于选项可以逐个验证，当判断框中填写i ≥10？时，输出结果为S ＝1 320；当判断框中填写i ≥11？时，输出结果为S ＝132；当判断框中填写i ≤11？时，输出结果为S ＝1；当判断框中填写i ≥12？时，输出结果为S ＝12.二、填空题7．将十进制数100转换成二进制数所得结果为______________． 答案 1 100 100(2)解析 以2作为除数相应得出的除法算式为：所以，100＝1 100 100(2)8．下边程序运行后，输出的值为________． S ＝1i＝1WHILE i<＝5 S ＝S*ii ＝i ＋1WEND PRINT S END答案 120解析 i ＝1时，S ＝1；i ＝2，S ＝2；i ＝3时，S ＝6； i ＝4时，S ＝6×4＝24，i ＝5时，S ＝24×5＝120； i ＝6时不满足i <＝5，执行“PRINT S ”，所以S ＝120.9．用辗转相除法求333与24的最大公约数时的循环次数为________． 答案 3次解析 333＝13×24＋21,24＝21＋3,21＝7×3， 共操作3次．三、解答题10．画出求12－22＋32－42＋…＋992－1002的值的程序框图． 解11．已知函数y ＝⎩⎪⎨⎪⎧2x 2－1 (x >0)2x ＋1 (x ＝0)－2x 2＋4 (x <0)，试编写程序，输入x 的值后输出y 的值．解 程序为：INPUT x IF x>0 THENy=2*x ＾2－1ELSEIF x=0 THENy=2*x+1 ELSEy=－2*x ＾2+4END IF END IFPRINT y END能力提升12．用秦九韶算法求多项式f(x)＝x 6＋2x 5＋3x 4＋4x 3＋5x 2＋6x 当x ＝2时的值． 解 f(x)＝x 6＋2x 5＋3x 4＋4x 3＋5x 2＋6x＝(((((x ＋2)x ＋3)x ＋4)x ＋5)x ＋6)x.所以有v 0＝1，v 1＝1×2＋2＝4，v 2＝4×2＋3＝11，v 3＝11×2＋4＝26，v 4＝26×2＋5＝57，v 5＝57×2＋6＝120，v 6＝120×2＝240.故当x ＝2时，多项式f(x)＝x 6＋2x 5＋3x 4＋4x 3＋5x 2＋6x 的值为240.13．某电信部门规定，拨打市内电话时，如果通话时间不超过3分钟，则收取通话费0.2元；如果通话时间超过3分钟，则超过部分按每分钟0.1元收取通话费(通话不足1分钟时按1分钟计)．试设计一个计算通话费用的算法，画出程序框图，并编写程序． 解 我们用C(单位：元)表示通话费，t(单位：分钟)表示通话时间，则依题意有C ＝⎩⎪⎨⎪⎧0.2 (t ∈N *，0<t ≤3)，0.2＋0.1(t －3) (t ∈N *，t >3). 算法步骤如下：第一步，输入通话时间t.第二步，如果t≤3，那么C＝0.2；否则，C＝0.2＋0.1×(t－3)．第三步，输出通话费用C.程序框图如图所示：程序如下：INPUT tIF t<=3 THENC=02ELSEC=0.2+0.1*(t-3)END IFPRINT CEND1．算法是对一类问题一般解法的抽象与概括，是把问题的解法划分为若干个可执行的步骤，有时需重复多次，但最终都必须在有限个步骤之内完成，所以在设计算法解决问题时要注意：(1)与解决问题的一般方法相联系，从中提炼出算法．(2)可引入有关的参数和变量对算法步骤加以表达．(3)解决问题的过程可分解为若干个步骤，并能用简洁实用的语言表达．(4)算法过程要便于在计算机上执行．2．程序框图是用规定的图形和指向线来形象、直观、准确的表示算法的图形．设计程序框图时，要先进行算法分析，确定算法的逻辑结构和各步的功能再画程序框图，同时要考虑到编写程序的要求．读、画程序框图是高考在本章中考查的重点．3．基本算法语句有输入语句、输出语句、赋值语句、条件语句和循环语句五种，主要对应顺序结构、条件结构和循环结构．明确各语句的功能和格式，是执行程序的关键，掌握常用的算法对理解程序也很有帮助，用算法语句编写程序时，一般先画程序框图．。

6.2.4 组合数（分层作业）（夯实基础+能力提升）【夯实基础】一、单选题 1．（2022春·甘肃兰州·高二校考期中）在含有3件次品的50件产品中，任取2件，则恰好取到1件次品的不同方法数共有（ ）A ．11347C CB ．20347C C C ．11349C CD ．1120347347C C C C +【答案】A【分析】根据组合的基本概念求解.【详解】在50件产品中含有3件次品,所以有47件不是次品, 任取2件，则恰好取到1件次品的不同方法数共有11347C C .2．（2022春·浙江·高二校联考阶段练习）2356C +C =（ ）A ．25B ．30C ．35D ．403．（2022春·辽宁葫芦岛·高二兴城市高级中学校联考阶段练习）已知3434，则x =（ ）A ．3或10B ．3C ．17D ．3或17【答案】A【分析】根据组合数的性质求解即可【详解】因为363434C C x x -=，故36x x =-或3634x x -=+，即3x =或10x = 二、多选题4．（2022·高二课时练习）下列问题中，属于组合问题的是（ ） A ．10支战队以单循环进行比赛（每两队比赛一次），共进行多少次比赛 B ．10支战队以单循环进行比赛，这次比赛的冠、亚军获得者有多少种可能 C ．从10名员工中选出3名参加同一种的娱乐活动，有多少种选派方法 D ．从10名员工中选出3名分别参加不同的娱乐活动，有多少种选派方法 【答案】AC【分析】区分一个具体问题是排列问题还是组合问题，关键是看它有无顺序.有顺序就是排列问题；无顺序就是组合问题,.【详解】A 是组合问题，因为每两个队进行一次比赛，并没有谁先谁后，没有顺序的区别.； B 是排列问题，因为甲队获得冠军、乙队获得亚军和甲队获得亚军、乙队获得冠军是不一样的，存在顺序区别；C 是组合问题，因为3名员工参加相同的活动，没有顺序区别；D 是排列问题，因为选的3名员工参加的活动不相同，存在顺序区别， 三、填空题5．（2023·高二课时练习）计算：0123444444C C C C C ++++=______．6．（2022秋·广东江门·高二台山市华侨中学校考期中）若n ，则______.【详解】解：2C C n n-=)530=，解得7．（2022秋·上海黄浦·高二上海市向明中学校考期末）若n n ，则正整数的值是______．8．（2022秋·河北唐山·高二校考期末）若1111C C =，则正整数x 的值是________．【答案】1或4【分析】解方程2x －1＝x 或2x －1＋x ＝11，即得解.【详解】解：∵211111C C x x-=，∴2x －1＝x 或2x －1＋x ＝11，解得x ＝1或x ＝4． 经检验，x ＝1或x ＝4满足题意.9．（2022秋·山东潍坊·高二统考阶段练习）若12C C 15m m +=，则m =_________．【答案】5【分析】利用组合数公式，列式求解作答.10．（2022秋·上海崇明·高二统考期末）已知x N ∈，则方程55的解是___________．【答案】1或2##2或1.【分析】根据组合数的性质列方程求解即可.【详解】因为2155C C x x -=，x N ∈，所以由组合数的性质得21x x =-或521x x -=-， 解得1x =或2x =，11．（2022秋·浙江·高二校联考期中）已知34C C m m =，则m =________．【答案】7【分析】根据组合数性质C C r n rn n -=分析即可. 【详解】因为C C r n rn n -=，故347m =+=.12．（2023·高二课时练习）设N x ∈，则123231C C x x x x ---++=______．【答案】4或7或11【分析】先由组合数的意义判断出2x =或3x =或4x =，分别代入求解.【详解】由组合数的意义可知：231123x x x x -≥-⎧⎨+≥-⎩，解得：24x ≤≤.又N x ∈，所以2x =或3x =或4x =.当2x =时，1231123113C C C C 4x x x x ---++=+=； 当3x =时，1232323134C C C C 347x x x x ---++=+=+=； 当4x =时，1233523155C C C C 10111x x x x ---++=+=+=.13．（2023·高二课时练习）若108C C n n =，则20C n的值为______．必须被选派的不同方案有______种． 【答案】35【分析】毕业生甲必须被选派，即从7人中选4人，计算得到答案.【详解】毕业生甲必须被选派的不同方案有47C 35=种.四、解答题15．（2021秋·广东广州·高二统考期末）平面内有A ，B ，C ，D ，E 共5个点． (1)以其中2个点为端点的线段共有多少条？ (2)以其中2个点为端点的有向线段共有多少条？(1)288A 6A x x -<(2)567117C C 10C m m m -=17．（2023·高二课时练习）在1，2，3，…，30这30个数中，每次取两两不等的三个数，使它们的和为3的倍数，共有多少种不同的取法？ 【答案】1360种【分析】将这30个数按除以3后的余数分为三类，分两种情况进行求解，再相加即可. 【详解】把这30个数按除以3后的余数分为三类：{}3,6,9,,30A =⋅⋅⋅，{}1,4,7,28B =⋅⋅⋅，{}2,5,8,,29C =⋅⋅⋅，每个集合各有10个元素．三个数的和为3的倍数的取法分两类：①在同一个集合中取三个数，有3103C 种取法；②在每个集合中各取一个数，有()3110C 种取法．由分类加法计数原理，共有()33110103C C 1360+=种不同的取法．18．（2023·高二课时练习）空间有10个点，其中任意4点不共面． (1)过每3个点作一个平面，一共可作多少个平面？(2)以每4个点为顶点作一个四面体，一共可作多少个四面体？ 【答案】(1)120个 (2)210个【分析】（1）（2）根据组合数的计算即可求解.【详解】（1）3个点确定一个平面，且任意4点不共面，所以从10个点中任选3个点即可构成一个平面，因此所有的平面个数为310C 120=（个）；（2）任意4点不共面，所以从10个点中任选4个点即可构成一个四面体，因此所有的四面体个数为410C 210=（个）；19．（2023·高二课时练习）有n 个人，每个人都以同样的概率被分配到N 个房间()n N ≤中的任意一间去，分别求下列事件的概率． (1)指定的n 间房中各有一人； (2)恰有n 间房，其中各有一人； (3)指定的某间房中恰有()m m n ≤人．一、单选题 1．（2022春·辽宁沈阳·高二沈阳二中校考阶段练习）沈阳二中24届篮球赛正如火如荼地进行中，全年级共20个班，每四个班一组，如1—4班为一组，5—8班为二组……进行单循环小组赛（没有并列），胜出的5个班级和从余下队伍中选出的数据最优秀的1个班级共6支球队按抽签的方式进行淘汰赛，最后胜出的三个班级再进行单循环赛，按积分的高低（假设没有并列）决出最终的冠亚季军，请问此次篮球赛学校共举办了多少场比赛？（ ） A ．51 B ．42 C ．39 D ．36【答案】D【分析】先进行单循环赛，6支球队按抽签的方式进行淘汰赛，最后3个班再进行单循环赛，分别求出所需比赛场次，即可得出答案. 【详解】先进行单循环赛，有245C =30场，胜出的5个班级和从余下队伍中选出的数据最优秀的1个班级共6支球队按抽签的方式进行淘汰赛，6支球队打3场，决出最后胜出的三个班， 最后3个班再进行单循环赛，由23C =3场. 所以共打了30+3+3=36场.2．（2022秋·山东聊城·高二山东聊城一中校考期中）因为疫情防控的需要，某校高二年级4名男教师和3名女教师参与社区防控新冠肺炎疫情的志愿服务．根据岗位需求应派3人巡视商户，且至少一名男教师；另外4人去不同的4个小区测量出入人员体温，则这7名教师不同的安排方法有（ ）种． A ．34 B ．816 C ．216 D ．210【答案】B【分析】先采用间接法求解巡视商户的3人中至少一名男教师的安排方法种数，然后再求解另外4人去不同的4个小区测量出入人员体温的安排方法种数，综合即可得出结果． 【详解】从7人中任选3人，不同的选法有37C 种，而不选男教师的选法有33C 种， 则巡视商户的3人中至少一名男教师安排方法有3373C C 34-=种，另外4人去不同的4个小区测量出入人员体温的安排方法有44A 24=种．则这7名教师不同的安排方法有3424816⨯=种．3．（2022春·新疆巴音郭楞·高二新疆和静高级中学校考阶段练习）中国空间站的主体结构包括天和核心实验舱､问天实验舱和梦天实验舱，假设空间站要安排甲､乙等6名航天员开展实验，三舱中每个舱至少一人至多三人，则不同的安排方法有（ ）种 A ．450 B ．72 C ．90 D ．3604．（2023·高二单元测试）设[]x 表示不超过x 的最大整数，如[]22=，514⎡⎤=⎢⎥⎣⎦．对于给定的。

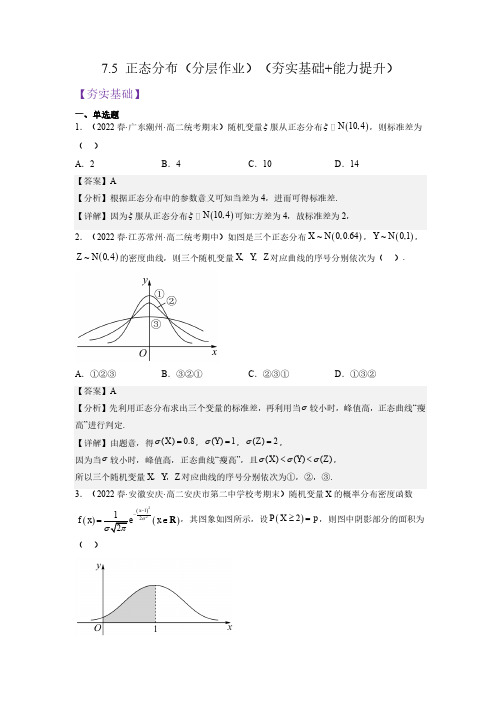
7.5 正态分布（分层作业）（夯实基础+能力提升）【夯实基础】一、单选题 1．（2022春·广东潮州·高二统考期末）随机变量ξ服从正态分布()10,4N ξ，则标准差为（ ） A ．2 B ．4C ．10D ．14【答案】A【分析】根据正态分布中的参数意义可知当差为4，进而可得标准差. 【详解】因为ξ服从正态分布()10,4N ξ可知:方差为4，故标准差为2，2．（2022春·江苏常州·高二统考期中）如图是三个正态分布()~0,0.64X N ，()~0,1Y N ，()~0,4Z N 的密度曲线，则三个随机变量X ，Y ，Z 对应曲线的序号分别依次为（ ）.A ．①②③B ．③②①C ．②③①D ．①③②【答案】A【分析】先利用正态分布求出三个变量的标准差，再利用当σ较小时，峰值高，正态曲线“瘦高”进行判定.【详解】由题意，得()0.8X σ=，()1Y σ=，()2Z σ=，因为当σ较小时，峰值高，正态曲线“瘦高”，且()()()X Y Z σσσ<<， 所以三个随机变量X ，Y ，Z 对应曲线的序号分别依次为①，②，③.3．（2022春·安徽安庆·高二安庆市第二中学校考期末）随机变量X 的概率分布密度函数()()()2212x f x x σ--=∈R ，其图象如图所示，设()2P X p ≥=，则图中阴影部分的面积为（ ）A ．pB ．2pC ．12p -D ．12p -A ．两个随机变量的线性相关性越强，则相关系数r 的绝对值越接近于0B ．若X 是随机变量，则()()()()2121,2141E X E X D X D X +=++=+.C ．已知随机变量()0,1N ξ，若(1)P p ξ>=，则(1)12P p ξ>-=-D ．设随机变量ξ表示发生概率为p 的事件在一次随机实验中发生的次数，则()14D ξ≤某中学参加网课的100名同学每天的学习时间（小时）服从正态分布()29,1N ，则这些同学中每天学习时间超过10小时的人数估计为（ ）. 附：随机变量ξ服从正态分布()2,N μσ，则()0.6826P μσξμσ-<<+=，()220.9544P μσξμσ-<<+=. A ．12 B ．16C ．30D ．32所以每天学习时间超过10小时的人数为1000.158716⨯≈，6．（2023秋·辽宁营口·高二统考期末）正常情况下，某厂生产的零件尺寸X 服从正态分布()22,N σ（单位：m ），()1.90.1P X <=，则()2.1P X <=（ ）A ．0.1B ．0.4C ．0.5D ．0.9【答案】D【分析】根据正态分布概率的对称性求解. 【详解】因为()()1.9 2.10.1P X P X <=>=， 所以()1.9 2.110.10.10.8P X <<=--=，所以()()()2.1 1.9 2.1 1.90.9P X P X P X <=<<+<=，7．（2022·高二课时练习）4月23日为世界读书日，已知某高校学生每周阅读时间（单位：h ）()8,4XN ，则下列说法错误的是（ ）A ．该校学生每周平均阅读时间为8hB ．该校学生每周阅读时间的标准差为2C ．若该校有10000名学生，则每周阅读时间在46h 的人数约为2718D ．该校学生每周阅读时间低于4h 的人数约占2.28% ()8,4N 知)100.6826≤≈46h 的人数约占(62P X -≤，所以C 错误；0.95442.28%=从N （90，2σ），若()90950.3P c ≤≤=，则可估计该班体能测试成绩低于85分的人数为（ ）A ．5B ．10C ．15D ．30则可估计该班体能测试成绩低于85分的人数为500.210⨯=人， 9．（2022春·山西忻州·高二统考期末）随机变量X 服从正态分布()2,N μσ，且(1)(5)P X P X >-=<，则下列说法一定正确的是（ ）A ．3μ=B ．2μ=C ．3σ=D ．2σ=分）服从正态分布()285,N σ，且(8387)0.3,(7883)0.26P P ξξ<≤=<≤=，则(78)P ξ≤=（ ）A ．0.03B ．0.05C ．0.07D ．0.0911．（2022春·江苏苏州·高二校考期末）在网课期间，为了掌握学生们的学习状态，某省级示范学校对高二一段时间的教学成果进行测试．高二有1 000名学生，某学科的期中考试成绩(百分制且卷面成绩均为整数)Z 服从正态分布()282.5,5.4N ，则(人数保留整数) （ ）参考数据：若20.682 7220.954 5()()()Z N P Z P Z μσμσμσμσμσ<≤≈<≤≈～，，则－＋，－＋，330.997 3()P Z μσμσ<≤≈－＋．A ．年级平均成绩为82.5分B ．成绩在95分以上(含95分)人数和70分以下(含70分)人数相等C ．成绩不超过77分的人数少于150D ．超过98分的人数为1 【答案】ABD【分析】根据正态分布的概念可知A 对，根据对称性可知B 对，根据3σ原则和曲线的对称性即可求解C,D.【详解】由()282.5,5.4N Z ～，可知82.5, 5.4μσ==，所以平均分为82.5μ=，故A 对.12．（2022春·重庆沙坪坝·高二重庆八中校考期末）已知121,X N σ~，220,Y N σ~，则下列结论中正确的是（ ）A ．若12σσ=，则()()10P X P Y >>>B ．若12σσ=，则()()101P X P Y >+>=C ．若12σσ>，则()()0211P X P Y ≤≤<-≤≤D ．若12σσ>，则()()0101P X P Y ≤≤>≤≤13．（2022春·云南昭通·高二校联考期末）设随机变量()2,X N μσ，X 的正态密度函数为()22x f x -，则μ=______.14．（2023秋·河南南阳·高二统考期末）已知随机变量ξ服从正态分布()210,N σ，若()310.5P a ξ≤+=，则实数=a ______．【答案】3【分析】由正态分布曲线的特点可知，得正态曲线关于10x =对称，且100.5PX ≤=（），结合题意得到a 的值．【详解】随机变量ξ服从正态分布()210,N σ，正态曲线关于10x =对称，且100.5PX ≤=（）， 由()310.5P a ξ≤+=，可知3110a +=，解得3a =．15．（2022春·重庆·高二校联考阶段练习）已知随机变量X 服从正态分布()2,N μσ，若()260.6P X <<=，()60.2P X ≥=，则μ=______． 【答案】4【分析】先求出()2P X ≤的概率，然后根据正态分布的特征求解即可. 【详解】解：由题意得：∵()()()()2162610.60.20.26P X P X P X P X ≤=-≥-<<=--==≥ ∴2与6关于x μ=对称 ∴4μ=．16．（2023秋·安徽宿州·高二安徽省泗县第一中学校考期末）某学校高二年级有1500名同学，一次数学考试的成绩X 服从正态分布()2110,10N ．已知(100110)0.34P X <≤=，估计高二年级学生数学成绩在120分以上的有__________人．17．（2023秋·辽宁葫芦岛·高二葫芦岛第一高级中学校考期末）随机变量X 服从正态分布，即()10,9X N ~，随机变量23Y X =-，则()E Y =__________，()D Y =__________． 【答案】 17 36【分析】首先根据正态分布的知识得()(),E X D X ，然后可得答案. 【详解】因为()10,9X N ~，所以()()10,9E X D X ==，因为23Y X =-，所以()()2320317E Y E X =-=-=，()()436D Y D X ==， 五、解答题18．（2023秋·河南南阳·高二统考期末）某车间生产一批零件，现从中随机抽取10个，测量其内径的数据如下（单位：mm ）：192，192，193，197，200，202，203，204，208，209．设这10个数据的均值为μ，标准差为σ． (1)求μ和σ；(2)已知这批零件的内径X （单位：mm ）服从正态分布()2,N μσ，若该车间又新购一台设备，安装调试后，试生产了5个零件，测量其内径（单位：mm ）分别为：181，190，198，204，213，如果你是该车间的负责人，以原设备生产性能为标准，试根据3σ原则判断这台设备是否需要进一步调试？并说明你的理由． 参考数据：若()2,XN μσ，则：()0.6826P X μσμσ-<≤+≈，()220.9544P X μσμσ-<≤+≈，()330.9974P X μσμσ-<≤+≈，40.99740.99≈． (200,36N )200180.9974+≈所以五个零件的内径中恰有1态分布()2N 500,5（单位：g ）．(1)求正常情况下，任意抽取一包白糖，质量小于485g 的概率约为多少？。

第6章 6.2.4A 级——基础过关练1．计算：C 28＋C 38＋C 29＝( ) A ．120 B ．240 C ．60D ．480【答案】A 【解析】C 28＋C 38＋C 29＝C 39＋C 29＝C 310＝120.2．有10个一模一样的小球,现分给甲、乙、丙3人,若甲至少得1球,乙至少得2球,丙至少得3球,则他们所得的球数的不同情形有( )A ．15B ．12C ．9D ．6【答案】A 【解析】首先分给甲1个球,乙2个球,丙3个球,还剩4个球． ①4个球分给1个人,有C 13＝3种分法； ②4个球分给2个人,有3C 23＝9种分法； ③4个球分给3个人,有3种分法． 共有3＋9＋3＝15(种)分法． 3．方程C x14＝C 2x －414的解集为( ) A ．{4} B ．{14} C ．{4,6}D ．{14,2}【答案】C 【解析】由题意知⎩⎪⎨⎪⎧x ＝2x －4，2x －4≤14，x ≤14或⎩⎪⎨⎪⎧x ＝14－2x －4，2x －4≤14，x ≤14，解得x＝4或6.4．有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )A ．60种B ．70种C ．75种D ．150种【答案】C 【解析】由题意知,选2名男医生、1名女医生的方法有C 26C 15＝75(种)． 5．从8名女生和4名男生中,抽取3名学生参加学校组织的活动,若按性别比例采用分层随机抽样,则不同的抽取方法数为( )A ．224B ．112C ．56D ．28【答案】B 【解析】由分层随机抽样知,应从8名女生中抽取2名,从4名男生中抽取1名,所以抽取2名女生和1名男生的方法数为C 28C 14＝112.6．若C m －18＞3C m8,则m 的值为________．【答案】7或8 【解析】由8！m －1！9－m ！＞3×8！m ！8－m ！,得m >27－3m ,所以m >274.又0≤m －1≤8,0≤m ≤8,m ∈N ,即7≤m ≤8,所以m ＝7或8.7．从进入决赛的6名选手中决出1名一等奖、2名二等奖、3名三等奖,则可能的决赛结果共有________种．【答案】60 【解析】利用排列组合知识列式求解．根据题意,所有可能的决赛结果有C 16C 25C 33＝6×5×42×1＝60(种)．8．在某互联网大会上,为了提升安保级别,将甲、乙等5名保安分配到3个不同的路口值勤,每个人只能分配到1个路口,每个路口最少分配1人,最多分配3人,且甲和乙不能安排在同一个路口,则不同的安排有________种．【答案】114 【解析】不考虑条件“甲和乙不能安排在同一个路口”,则有两种情况： ①3个路口人数分别为3,1,1时,安排方法共有C 35·A 33＝60(种)； ②3个路口人数分别为2,2,1时,安排方法有C 25·C 23A 22·A 33＝90(种)．若将甲、乙安排在同一个路口,安排法有C 24·A 33＝36(种), 故甲和乙不安排在同一路口的方法共有60＋90－36＝114(种)．9．某餐厅供应饭菜,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种．现在餐厅准备了5种不同的荤菜,若要保证每位顾客有200种以上不同的选择,则餐厅至少还需准备多少不同的素菜品种？解：设餐厅至少还需准备x 种不同的素菜．由题意,得C 25·C 2x ≥200,从而有C 2x ≥20,即x (x －1)≥40.又x ≥2且x ∈N *,所以x 的最小值为7.10．把12个一模一样的球放入编号为1,2,3,4的盒子中,要求每个盒子中的小球个数不小于其编号数,则不同放法有几种？解：给每个盒子放入与其编号数相同的小球,则还剩2个小球．这2个小球可以放在1个或2个盒子中,故不同的放法有C 14＋C 24＝10(种)．B 级——能力提升练11．若C 7n ＋1－C 7n ＝C 8n ,则n 等于( ) A ．12 B ．13 C ．14D ．15【答案】C 【解析】 因为C 7n ＋1－C 7n ＝C 8n ,即C 7n ＋1＝C 8n ＋C 7n ＝C 8n ＋1,所以n ＋1＝7＋8,即n ＝14.12．某施工小组有男工7名,女工3名,现要选1名女工和2名男工去支援另一施工队,不同的选法有( )A ．C 310种 B ．A 310种 C ．A 27A 13种D ．C 27C 13种【答案】D 【解析】 每个被选的人员无角色差异,是组合问题．分两步完成：第一步,选女工,有C 13种选法；第二步,选男工,有C 27种．故有C 13C 27种不同选法．13．现有12张不同的卡片,其中红色、黄色、蓝色、绿色卡片各3张,从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张,不同的取法种数为( )A ．135B ．172C ．189D ．162【答案】C 【解析】 不考虑特殊情况,共有C 312种取法,取3张相同颜色的卡片,有4种取法,只取2张红色卡片(另一张非红色),共有C 23C 19种取法．所求取法种数为C 312－4－C 23C 19＝189.14．口袋里装有大小相同的黑白两色的手套,黑色手套15只,白色手套10只．现从中随机抽取出两只手套,若两只是同色手套,则甲获胜,若两只手套颜色不同,则乙获胜,则甲、乙获胜的机会是( )A ．甲多B ．乙多C ．一样多D ．不确定【答案】C 【解析】两只是同色手套的取法有C 215＋C 210＝150(种)；两只不是同色手套的取法有C 115·C 110＝150(种)．15．从2,3,5,7四个数中任取两个不同的数相乘,有m 个不同的积；任取两个不同的数相除,有n 个不同的商,则m ∶n ＝________.【答案】1∶2 【解析】∵m ＝C 24,n ＝A 24,∴m ∶n ＝1∶2.16．从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有________种不同的选法(用数字作答)．【答案】660 【解析】总的选法为C 48C 14C 13种,其中不满足条件的选法为C 46C 14C 13种,则满足条件的选法为C 48C 14C 13－C 46C 14C 13＝660(种)．17．已知10件不同产品中有4件是次品,现对它们进行一一测试,直至找出所有次品为止． (1)若恰在第5次测试,才测试到第一件次品,第10次测试才找到最后一件次品,则这样的不同测试方法数是多少？(2)若恰在第5次测试后,就找出了所有4件次品,则这样的不同测试方法数是多少？ 解：(1)先排前4次测试,只能取正品,有A 46种不同的测试方法,再从4件次品中选2件排在第5和第10的位置上测试,有C 24·A 22＝A 24(种)测法,再排余下4件的测试位置,有A 44种测法．所以共有不同测试方法A 46·A 24·A 44＝103 680(种)．(2)第5次测试恰为最后一件次品,另3件在前4次中出现,从而前4次有一件正品出现,所以共有不同测试方法C 14·(C 16·C 33)A 44＝576(种)．C 级——探究创新练18．已知C 4n ,C 5n ,C 6n 成等差数列,求C 12n 的值． 解：由已知得2C 5n ＝C 4n ＋C 6n , 所以2·n ！5！n －5！＝n ！4！n －4！＋n ！6！n －6！,整理得n 2－21n ＋98＝0,解得n ＝7或n ＝14, 要求C 12n 的值,故n ≥12,所以n ＝14, 于是C 1214＝C 214＝14×132×1＝91.。

章末综合检测(一)(时间：120分钟，满分：150分)一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．下列给出的赋值语句正确的是( ) A ．3＝A B ．M ＝－M C ．B ＝A ＝2 D ．x ＋y ＝0解析：选B.赋值语句的格式为“变量＝表达式”，故只有B 正确，故选B.2．在设计求函数f (x )＝⎩⎪⎨⎪⎧x 2，x >2x －1，－2<x ≤26x －6，x ≤－2的值的程序中不可能用到的算法语句为( )A ．输入语句B ．条件语句C ．输出语句D ．循环语句解析：选D.对于分段函数的算法，输入语句和输出语句都是需要的，条件语句也是需要的，只有循环语句不可能用到，故选D.3．如图所示的程序框图，已知a 1＝3，输出的结果为7，则a 2的值是( )A ．9B ．10C ．11D ．12解析：选C.按程序框图逆向求值．因为输出的结果为7，所以b ＝7，又b ＝b2，所以原b ＝14，即a 1＋a 2＝14.又a 1＝3，所以a 2＝11.4．在k 进制中，十进制数103记为87，则k 等于( ) A ．6 B ．12 C ．14 D ．16解析：选B.由k 进制中基数为k ，得8×k ＋7×k 0＝103，即8k ＝96，k ＝12.故选B. 5．执行如图所示的程序框图，输出的结果为( )A ．6B ．24C ．120D ．48 解析：选B.当n ＝5时，结束循环，s ＝1×2×3×4＝24，故选B. 6．执行如图所示的程序框图，则输出S 的值为( )A ．2 016B ．2 C.12D ．－1解析：选B.S ＝2，k ＝0，满足条件k <2 016，则S ＝－1，k ＝1；满足条件k <2 016，则S ＝12，k ＝2；满足条件k <2 016，则S ＝2，k ＝3；满足条件k <2 016，则S ＝－1，k ＝4；满足条件k <2 016，则S ＝12，k ＝5；….观察规律，可知S 的取值以3为周期变化，当k ＝2 015＝3×671＋2时，满足条件k <2 016，则S ＝2，k ＝2 016，结束循环，输出2.故选B.7A ．17B ．19C ．21D ．23解析：选C.第一次循环，i＝3，S＝9，i＝2；第二次循环，i＝4，S＝11，i＝3；第三次循环，i＝5，S＝13，i＝4；第四次循环，i＝6，S＝15，i＝5；第五次循环，i＝7，S＝17，i＝6；第六次循环，i＝8，S＝19，i＝7；第七次循环，i＝9，S＝21，i＝8.此时i＝8，不满足i＜8，故退出循环，输出S＝21，结束．8．阅读如图程序框图，如果输出i＝5，那么在空白矩形框中应填入的语句为()A．S＝2i－2 B．S＝2i－1C．S＝2i D．S＝2i＋4解析：选C.当空白矩形框中应填入的语句为S＝2i时，程序在运行过程中各变量的值如下所示：i S是否继续循环循环前10第一次循环25是第二次循环36是第三次循环49 是第四次循环510 否故输出的i值为5，符合题意．故选C.9．执行如图所示的程序框图，如果最后输出的s的值为110，那么判断框中实数a的取值范围是()A ．[9，10)B ．(9，10]C ．[9，10]D ．无法确定解析：选A.s ＝12，n ＝2；s ＝13，n ＝3；s ＝14，n ＝4；s ＝15，n ＝5；…；s ＝110，n ＝10，故9≤a <10，故选A.10．已知图象不间断的函数f (x )是区间[a ，b ]上的单调函数，且在区间(a ，b )上存在零点．如图是用二分法求方程f (x )＝0近似解的程序框图，判断框内可填写的内容有如下四个选择：①f (a )f (m )＜0；②f (a )f (m )＞0； ③f (b )f (m )＜0；④f (b )f (m )＞0.其中能够正确求出近似解的是( )A ．①③B ．②③C ．①④D ．②④解析：选C.如果f (a )f (m )＜0，此时解在区间(a ，m )内，令b ＝m 后近似解就在区间(a ，b )内，否则解在区间(m ，b )内，此时应该把m 值赋给a ，故判断条件f (a )f (m )＜0可以求出方程的近似解，而且这个条件等价于f (b )f (m )＞0，故选C.11．某店一个月的收入和支出总共记录了N 个数据a 1，a 2，…，a N ，其中收入记为正数，支出记为负数．该店用如图所示的程序框图计算月总收入S 和月净盈利V ，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的( )A ．A >0？，V ＝S －TB ．A <0？，V ＝S －TC ．A >0？，V ＝S ＋TD ．A <0？，V ＝S ＋T解析：选C.由题意可得，判断框内应填“A >0？”，月净盈利V 为S 与T 的和，故处理框中填“V ＝S ＋T ”，所以选C.12．执行如图所示的程序框图，如果输入的t ＝0.01，则输出的n ＝( )A ．5B ．6C ．7D ．8解析：选C.经推理分析可知，若程序能满足循环，则每循环一次，S 的值减少一半，循环6次后S 的值变为126＝164>0.01，循环7次后S 的值变为127＝1128<0.01，此时不再满足循环的条件，所以结束循环，于是输出的n ＝7.二、填空题：本题共4小题，每小题5分．13．用辗转相除法计算56和264的最大公约数时，需要做的除法次数是__________． 解析：由辗转相除法，264＝56×4＋40；56＝40×1＋16；40＝16×2＋8；16＝8×2.即得最大公约数为8，做了4次除法．答案：414．执行如图所示的程序框图，当输入的值为3时，输出的结果是________．解析：3<5，执行y＝x2－1，所以输出结果为8.答案：815．如图，是用辗转相除法求两个正整数a，b(a＞b)的最大公约数算法的程序框图，其中①处应填入的是________．解析：根据辗转相除法的原理，易知①处应填入的是r＝a MOD b.答案：a MOD b16．某程序框图如图所示，若使输出的结果不大于37，则输入的整数i的最大值为________．解析：S＝(20＋1)＋(21＋1)＋(22＋1)＋…＋(2i－1＋1)．当i＝1时，S＝2；当i＝2时，S＝2＋3＝5；当i＝3时，S＝2＋3＋5＝10；当i＝4时，S＝2＋3＋5＋9＝19；当i＝5时，S＝2＋3＋5＋9＋17＝36；当i＝6时，S＝2＋3＋5＋9＋17＋33＝69＞37.所以，i 的最大值为5. 答案：5三、解答题：解答应写出文字说明、证明过程或演算步骤． 17．(本小题满分10分)用秦九韶算法计算函数f (x )＝2x 5＋3x 4＋2x 3－4x ＋5当x ＝2时的函数值．解：根据秦九韶算法，把多项式改写成如下形式： f (x )＝((((2x ＋3)x ＋2)x ＋0)x －4)x ＋5.从内到外依次计算一次多项式当x ＝2时的值： v 0＝2；v 1＝2×2＋3＝7； v 2＝v 1×2＋2＝16； v 3＝v 2×2＋0＝32； v 4＝v 3×2－4＝60； v 5＝v 4×2＋5＝125.所以，当x ＝2时，多项式的值等于125.18．(本小题满分12分)已知函数f (x )＝⎩⎪⎨⎪⎧x 2－1，x ≥0，2x 2－5，x <0，对每输入的一个x 值，都得到相应的函数值．画出程序框图并写出程序．解：程序框图如图：(1)指出程序所用的是何种循环语句，并指出该程序的算法功能；(2)请用另一种循环语句的形式把该程序写出来．解：(1)本程序所用的循环语句是WHILE循环语句，其功能是计算12＋22＋32＋…＋92的值．(2)用UNTIL20．(本小题满分12分)分别用WHILE语句和UNTIL语句编写程序，求出使不等式12＋22＋32＋…＋n2<1 000成立的n的最大整数值．解：利用利用21．(本小题满分12分)某中学男子体育组的百米赛跑的成绩(单位：秒)如下：12.1，13.2，12.7，12.8，12.5，12.4，12.7，11.5，11.6，11.7.设计一个算法从这些成绩中搜索出所有小于12.1秒的成绩，画出程序框图，并编写相应的程序．解：程序框图如图：程序：22．(本小题满分12分)已知某算法的程序框图如图所示，若将输出的(x，y)值依次记为(x1，y1)，(x2，y2)，…，(x n，y n)，…(1)若程序运行中输出的一个数组是(9，t)，求t的值；(2)程序结束时，共输出(x，y)的组数为多少；(3)写出程序框图的程序语句．解：(1)开始时，x＝1时，y＝0；接着x＝3，y＝－2；然后x＝9，y＝－4，所以t＝－4.(2)当n＝1时，输出一对，当n＝3时，又输出一对，…，当n＝2 015时，输出最后一对，共输出(x，y)的组数为1 008.(3)。

6.2.1排列（分层作业）（夯实基础+能力提升）【夯实基础】一、单选题 1．（2022春·吉林四平·高二四平市第一高级中学校考阶段练习）下列问题是排列问题的是（ ） A ．10个朋友聚会，每两人握手一次，一共握手多少次？B ．平面上有2022个不同的点，且任意三点不共线，连接任意两点可以构成多少条线段？C ．集合{}123,,,,n a a a a ⋅⋅⋅的含有三个元素的子集有多少个？D ．从高三（19）班的54名学生中选出2名学生分别参加校庆晚会的独唱、独舞节目，有多少种选法？ 【答案】D【分析】根据排列的定义逐个选项辨析即可.【详解】A 中握手次数的计算与次序无关，不是排列问题； B 中线段的条数计算与点的次序无关，不是排列问题； C 中子集的个数与该集合中元素的次序无关，不是排列问题；D 中，选出的2名学生，如甲、乙，其中“甲参加独唱、乙参加独舞”与“乙参加独唱、甲参加独舞”是2种不同的选法，因此是排列问题．2．（2022秋·吉林长春·高二长春市第二实验中学校考期中）从5本不同的书中选出3本分别送3位同学每人一本，不同的方法总数是（ ） A ．10 B ．60 C ．243 D ．15【答案】B【分析】根据排列定义即可求解．【详解】不同的方法总数是35A 54360=⨯⨯=3．（2022春·吉林四平·高二四平市第一高级中学校考阶段练习）从6名员工中选出3人分别从事教育、培训、管理三项不同的工作，则选派方案共有（ ） A ．60种 B ．80种 C ．100种 D ．120种【答案】D【分析】利用排列的定义直接列式求解.【详解】从6名员工中选出3人分别从事教育、培训、管理三项不同的工作，则选派方案共36654120A =创=（种）．4．（2022·高二课时练习）从集合{}3,5,7,9,11中任取两个元素，①相加可得多少个不同的和？②相除可得多少个不同的商？③作为椭圆()222210,0x y a b a b+=>>中的a ，b ，可以得到多少个焦点在x 轴上的椭圆方程？④作为双曲线()222210,0x y a b a b -=>>中的a ，b ，可以得到多少个焦点在x 轴上的双曲线方程？上面四个问题属于排列问题的是（ ） A ．①②③④ B ．②④C ．②③D ．①④演讲比赛，在安排出场顺序时，小红、小明排在一起，且小芳与小红、小明都不相邻的概率为（ ） A ．110 B ．16C ．15D ．25字比个位数字和百位数字都大，则称这个数为“伞数”，现从1,2,3,4,5这5个数字中任取3个数字，组成没有重复数字的三位数，其中“伞数”共有（ ）个. A ．60 B ．35C ．20D ．53【答案】C【分析】根据的“伞数”定义，十位数只能是3，4，5，然后分3类，分别求得“伞数”的个数再求和，【详解】由题意得：十位数只能是3，4，5，当十位数是3时，个位和百位只能是1，2，“伞数”共有22A 2=个； 当十位数是4时，个位和百位只能是1，2，3，“伞数”共有23A 6=个；当十位数是5时，个位和百位只能是1，2，3，4，“伞数”共有24A 12=个；所以“伞数”共有20个，7．（2022春·河南南阳·高二校考阶段练习）为庆祝中国共青团成立100周年，某校计划举行庆祝活动，共有4个节目，要求A 节目不排在第一个，则节目安排的方法数为（ ） A ．9 B ．18 C ．24 D ．27【答案】B【分析】由于A 节目有特殊要求，所以先安排A 节目，再安排其它的节目，从而即可求解. 【详解】解：由题意，先从后面3个节目中选择一个安排A 节目，然后其它3个节目任意排在剩下的3个位置，共有1333C A 18=种方法，二、填空题8．（2023·高二课时练习）给出下列问题：①有10位同学，每两人互通一次电话，共通了多少次电话？ ②有10位同学，每两人互写一封信，共写了多少封信？ ③有10位同学，每两人互握一次手，共握了多少次手？以上问题中，属于排列问题的是______．（写出所有满足要求的问题序号） 【答案】②【分析】根据排列的定义判断即可【详解】对于①，假设10位同学中含甲乙，甲与乙通一次电话，也就是乙与甲通一次电话，没有顺序区别，故不是排列问题；对于②，假设10位同学中含甲乙，甲给乙写一封信，跟乙给甲写一封信，是不一样的，是有顺序区别的，故属于排列问题；对于③，假设10位同学中含甲乙，甲与乙握一次手，也就是乙与甲握一次手，没有顺序区别，故不是排列问题，9．（2023·高二课时练习）若N m ∈，且27m <，则()()()272834m m m --⋅⋅⋅-用排列记号可表示为______． 【答案】834P m -【分析】利用排列数的定义直接表示.【详解】由排列数的定义，()()()834272834P m m m m ---⋅⋅⋅-=.10．（2022秋·广东广州·高二广州市天河中学校考期中）从4本不同的课外读物中，买3本送给3名同学，每人各1本，则不同的送法种数是______．【答案】24【分析】直接根据排列数的意义求解即可【详解】由题意，不同的送法种数为34A 24N ==.11．（2023·高二课时练习）给出下列问题：①从2、3、5、7、11中任取两数相乘，可得多少个不同的积？ ②从2、3、5、7、11中任取两数相除，可得多少个不同的商？ ③从2、3、5、7、11中任取两数相加，可得多少个不同的和？以上问题中，属于排列问题的是______．（写出所有满足要求的问题序号） 【答案】②【分析】根据排列的定义，关键是确定选取的两个数有无顺序【详解】对于①，从2、3、5、7、11中任取两数相乘，且乘法满足交换律，故不是排列问题; 对于②，从2、3、5、7、11中任取两数相除，且除法不满足交换律，故是排列问题; 对于③，从2、3、5、7、11中任取两数相加，且加法满足交换律，故不是排列问题;12．（2023·高二课时练习）计算：66248108!A A A +=-______． )()()()21121，A n mm m m m n ⨯=---+，57720579051305689789623⨯⨯=-=--⨯⨯. 高二四平市第一高级中学校考阶段练习）冬奥会首金诞生于短道速滑男女混合接力赛，赛后4位运动员依次接受采访，曲春雨要求不第1个接受采访，武大靖在任子威后接受采访（可以不相邻），则采访安排方式有__________种． 14．（2023·高二课时练习）从甲、乙、丙三名学生中任意安排2名学生参加数学、外语两个课外小组的活动，共有多少种不同的安排方案？请画出相应的树状图，并解答． 【答案】共6种安排方案，树状图见解析【分析】根据题意画出树状图即可求解 【详解】树状图如图所示，由树状图可知，共有6种不同的安排方案15．（2022秋·山西吕梁·高二校考阶段练习）用0，1，2，3，4，5这六个数字组成无重复数字的整数，求满足下列条件的数各有多少个． (1)六位奇数；(2)能被5整除的四位数. 【答案】(1)288 (2)108【分析】先排个位，再排首位，最后排中间四位.【详解】（1）先排个位，个位数字只能从1，3，5中选，有3种方法； 再排首位，首位不能为0，故还有4个数字可选，有4种方法； 最后排中间四位，没有其他附加条件，排列数为4!.由分步乘法计数原理，知共有不同的排法种数为344!288⨯⨯=.（2）能被5整除，个位只能是0或5，个位是0时，没有其他附加条件，其他三个数位的排法有35A 种；个位是5时，首位排法有4种，再排十位与百位，有24A 种，所以个位是5的排法有244A 种.由分类加法计数原理知共有4352108A 4A +=种排法.16．（2022春·吉林四平·高二四平市第一高级中学校考阶段练习）现有8个人（5男3女）站成一排．(1)其中甲必须站在排头有多少种不同排法？ (2)女生必须排在一起，共有多少种不同的排法？ (3)其中甲、乙两人不能排在两端有多少种不同的排法？ (4)其中甲在乙的左边有多少种不同的排法？ (5)甲、乙不能排在前3位，有多少种不同排法？ (6)女生两旁必须有男生，有多少种不同排法？ 【答案】(1)5040 (2)4320 (3)21600 (4)20160 (5)14400 (6)2880一、单选题 1．（2022秋·山东菏泽·高二统考期末）将诗集《诗经》、《唐诗三百首》，戏剧《牡丹亭》，四大名著《红楼梦》、《西游记》、《三国演义》、《水浒传》7本书放在一排，下面结论成立的是（ ）A ．戏剧放在中间的不同放法有7!种B ．诗集相邻的不同放法有6!种C ．四大名著互不相邻的不同放法有4!3!⨯种D ．四大名著不放在两端的不同放法有64!⨯种 【答案】C【分析】根据分步乘法计数原理计数后进行判断即可.。

[A 基础达标]1．某银行储蓄卡上的密码是一个6位数号码，每位上的数字可以在0～9这10个数字中选取．某人未记住密码的最后一位数字，如果随意按密码的最后一位数字，则正好按对密码的概率是( )A.1106B.1105C.1102D.110解析：选D.只考虑最后一位数字即可，从0到9这10个数字中随机选一个的概率为110. 2．袋子中有四个小球，分别写有“幸”“福”“快”“乐”四个字，有放回地从中任取一个小球，取到“快”就停止，用随机模拟的方法估计直到第二次停止的概率：先由计算器产生1到4之间取整数值的随机数，且用1，2，3，4表示取出小球上分别写有“幸”“福”“快”“乐”四个字，以每两个随机数为一组，代表两次的结果，经随机模拟产生了20组随机数：13 24 12 32 43 14 24 32 31 2123 13 32 21 24 42 13 32 21 34据此估计，直到第二次就停止的概率为( )A.15B.14C.13D.12 解析：选B.由随机模拟产生的随机数可知，直到第二次停止的有13，43，23，13，13共5个基本事件，故所求的概率为P ＝520＝14. 3．通过模拟试验，产生了20组随机数：6830 3013 7055 7430 7740 4422 78842604 3346 0952 6807 9706 5774 57256576 5929 9768 6071 9138 6754如果恰有三个数在1，2，3，4，5，6中，则表示恰有三次击中目标，问四次射击中恰有三次击中目标的概率约为( )A ．25%B ．30%C ．35%D ．40%解析：选A.表示三次击中目标分别是3013，2604，5725，6576，6754，共5组数，而随机数总共20组，所以所求的概率近似为520＝25%. 4．假定某运动员每次投掷飞镖正中靶心的概率为40%，现采用随机模拟的方法估计该运动员两次投掷飞镖恰有一次命中靶心的概率：先由计算器产生0到9之间取整数值的随机数，指定1，2，3，4表示命中靶心，5，6，7，8，9，0表示未命中靶心；再以每两个随机数为一组，代表两次的结果，经随机模拟产生了20组随机数：93 28 12 45 85 69 68 34 31 2573 93 02 75 56 48 87 30 11 35据此估计，该运动员两次掷镖恰有一次正中靶心的概率为( )A ．0.50B ．0.45C ．0.40D ．0.35解析：选A.两次掷镖恰有一次正中靶心表示随机数中有且只有一个数为1，2，3，4中的之一．它们分别是93，28，45，25，73，93，02，48，30，35共10个，因此所求的概率为1020＝0.50. 5．某种心脏病手术，成功率为0.6，现准备进行3例此种手术，利用计算机取整数值随机数模拟，用0，1，2，3代表手术不成功，用4，5，6，7，8，9代表手术成功，产生20组随机数：966，907，191，924，270，832，912，468，578，582，134，370，113，573，998，397，027，488，703，725，则恰好成功1例的概率为( )A ．0.6B ．0.4C ．0.63D ．0.43解析：选B.设恰好成功1例的事件为A ，A 所包含的基本事件为191，270，832，912，134，370，027，703共8个．则恰好成功1例的概率为P (A )＝820＝0.4，故选B. 6．抛掷两枚相同的骰子，用随机模拟方法估计向上的面的点数和是6的倍数的概率时，用1，2，3，4，5，6分别表示向上的面的点数，用计算器或计算机分别产生1到6的两组整数随机数各60个，每组第i 个数组成一组，共组成60组数，其中有一组是16，这组数表示的结果是否满足向上面的点数和是6的倍数：________．(填“是”或“否”)解析：16表示第一枚骰子向上的点数是1，第二枚骰子向上的点数是6，则向上的面的点数和是1＋6＝7，不表示和是6的倍数．答案：否7．从集合{a ，b ，c ，d }的子集中任取一个，这个集合是集合{a ，b ，c }的子集的概率是________．解析：集合{a ，b ，c ，d }的子集有∅，{a }，{b }，{c }，{d }，{a ，b }，{a ，c }，{a ，d }，{b ，c }，{b ，d }，{c ，d }，{a ，b ，c }，{a ，b ，d }，{b ，c ，d }，{a ，c ，d }，{a ，b ，c ，d }，共16个，{a ，b ，c }的子集有∅，{a }，{b }，{c }，{a ，b }，{a ，c }，{b ，c }，{a ，b ，c }，共8个，故所求概率为12. 答案：128．某汽车站每天均有3辆开往省城的分为上、中、下等级的客车，某天袁先生准备在该汽车站乘车前往省城办事，但他不知道客车的车况，也不知道发车顺序．为了尽可能乘上上等车，他采取如下策略：先放过一辆，如果第二辆比第一辆好则上第二辆，否则上第三辆，则他乘上上等车的概率为________．解析：共有6种发车顺序：①上、中、下；②上、下、中；③中、上、下；④中、下、上；⑤下、中、上；⑥下、上、中(其中画横线的表示袁先生所乘的车)，所以他乘坐上等车的概率为36＝12. 答案：129．天气预报说，在接下来的一个星期里，每天涨潮的概率为20%，则下个星期恰有2天涨潮的概率是多少？解：利用计算机产生0～9之间取整数值的随机数，用1，2表示涨潮，用其他数字表示不涨潮，这样体现了涨潮的概率是20%，因为时间是一周，所以每7个随机数作为一组，例如产生20组随机数：7032563 2564586 3142486 56778517782684 6122569 5241478 89715683215687 6424458 6325874 68943315789614 5689432 1547863 35698412589634 1258697 6547823 2274168相当于做了20次试验，在这组数中，如果恰有两个是1或2，就表示恰有两天涨潮，它们分别是3142486，5241478，3215687，1258697，共有4组数，于是一周内恰有两天涨潮的概率近似值为420＝20%. 10．一个学生在一次竞赛中要回答8道题是这样产生的：从15道物理题中随机抽取3道；从20道化学题中随机抽取3道；从12道生物题中随机抽取2道．使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为1～15，化学题的编号为16～35，生物题的编号为36～47)．解：利用计算器的随机函数RANDI(1，15)产生3个不同的1～15之间的整数随机数(如果有一个重复，则重新产生一个)；再利用计算器的随机函数RANDI(16，35)产生3个不同的16～35之间的整数随机数(如果有一个重复，则重新产生一个)；再用计算器的随机函数RANDI(36，47)产生2个不同的36～47之间的整数随机数(如果有一个重复，则重新产生一个)，这样就得到8道题的序号．[B 能力提升]11．某班准备到郊外野营，为此向商店订了帐篷，如果下雨与不下雨是等可能的，能否准时收到帐篷也是等可能的，只要帐篷如期运到，他们就不会淋雨，则下列说法正确的是( )A ．一定不会淋雨B ．淋雨的机会为34C ．淋雨的机会为12D ．淋雨的机会为14解析：选D.根据题意，用1代表下雨，2代表不下雨，用A 代表中帐篷如期运到，B 代表没有如期运到，采用模拟法得到基本事件有(1，A )，(1，B )，(2，A )，(2，B )这4种情况．若淋雨必须满足天下雨且帐篷没有如期运到，这一基本事件发生即只有(1，B )1种情况发生，故淋雨的机会为14. 12．在用随机(整数)模拟求“有4个男生和5个女生，从中取4个，求选出2个男生2个女生”的概率时，可让计算机产生1～9的随机整数，并用1～4代表男生，用5～9代表女生．因为是选出4个，所以每4个随机数作为一组．若得到的一组随机数为“4678”，则它代表的含义是________．答案：选出的4人中，只有1个男生13．某人有5把钥匙，其中2把能打开门，现随机地取1把钥匙试着开门，不能开门就扔掉，问第三次才打开门的概率是多少？如果试过的钥匙不扔掉，这个概率又是多少？设计一个试验，随机模拟估计上述概率．解：用计算器或计算机产生1到5之间的整数随机数，1，2表示能打开门，3，4，5表示打不开门．(1)三个一组(每组数字不重复)，统计总组数N 及前两个大于2，第三个是1或2的组数N 1，则N 1N即为不能打开门就扔掉，第三次才打开门的概率的近似值． (2)三个一组(每组数字可重复)，统计总组数M 及前两个大于2，第三个为1或2的组数M 1，则M 1M即为试过的钥匙不扔掉，第三次才打开门的概率的近似值． 14．(选做题)某商区停车场临时停车按时段收费，收费标准为：每辆汽车一次停车不超过1小时收费6元，超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算)，现有甲、乙二人在该商区临时停车，两人停车都不超过4小时．(1)若甲停车1小时以上且不超过2小时的概率为13，停车付费多于14元的概率为512，求甲停车付费恰为6元的概率；(2)若每人停车的时长在每个时段的可能性相同，求甲、乙二人停车付费之和为36元的概率．解：(1)设“甲临时停车付费恰为6元”为事件A ，则P (A )＝1－⎝⎛⎭⎫13＋512＝14.所以甲临时停车付费恰为6元的概率是14. (2)设甲停车付费a 元，乙停车付费b 元，其中a ，b ＝6，14，22，30.则甲、乙二人的停车费用共16种等可能的结果：(6，6)，(6，14)，(6，22)，(6，30)，(14，6)，(14，14)，(14，22)，(14，30)，(22，6)，(22，14)，(22，22)，(22，30)，(30，6)，(30，14)，(30，22)，(30，30)，其中(6，30)，(14，22)，(22，14)，(30，6)4种情形符合题意．所以“甲、乙二人停车付费之和为36元”的概率为P ＝416＝14.。

6.2.2 排列数（分层作业）（夯实基础+能力提升）【夯实基础】一、单选题 1．（2022秋·云南楚雄·高二云南省楚雄第一中学校考阶段练习）从3，5，7，11这四个质数中，每次取出两个不同的数分别为,a b ，共可得到lg lg a b -的不同值的个数是（ ） A ．6 B ．8 C ．12 D ．16若甲不站在两端，不同排列方式有（ ） A ．6种 B ．12种 C ．36种 D ．48种【答案】B【分析】题目关键点为甲不站在两端，则甲站中间2个位置，先排好甲以后，剩余3个位置其余的三位同学进行全排列即可.【详解】甲站位的排列数为12A ，其余三位学生的全排列数为33A ， 所有的排列方式有：1323A A 232112=⨯⨯⨯=.3．（2022春·江西上饶·高二校联考阶段练习）现从6名学生干部中选出3名同学分别参加全校资源、生态和环保3个夏令营活动，则不同的选派方案的种数是（ ） A ．20 B ．90 C ．120 D ．240【答案】C【分析】根据排列可求不同的选派方案的种数.【详解】共有36A 120=种不同的选派方案．4．（2022秋·山东菏泽·高二统考期中）若A 230n =，则n =（ ）A ．4B ．5C ．6D ．7【答案】C【分析】根据排列数的计算公式，列出方程，即可求解.【详解】由排列数的计算公式，可得22(1)n n n n n A =-=-，且2,N n n ≥∈， 因为230n A =，即2300n n --=，解得6n =或5n =-（舍去）.5．（2022春·福建莆田·高二莆田第六中学校考阶段练习）6名同学站成一排照相，其中甲、乙两人必须相邻的站法有（ ）种A ．240B ．288C ．48D ．580【答案】A【分析】利用排列组合中的捆绑法即可得解.【详解】第一步：将甲、乙两人捆绑在一起，看作一个元素，与剩下的4名同学进行排列，则有55A 54321120=⨯⨯⨯⨯=种方法，第二步：甲、乙两人内部可以进行排列，有22A 212=⨯=种方法，所以一共有1202240⨯=种方法. 二、多选题6．（2022秋·江苏南京·高二校考期中）下列各式中，等于!n 的是（ ） A ．!A m n m B ．1A n n + C ．n 1n A - D ．11A n n n --7．（2022春·吉林四平·高二四平市第一高级中学校考阶段练习）已知2330A A 2!4m+=-，则m 的可能取值是（ ）A ．0B ．1C ．2D ．38．（2022秋·吉林·高二校联考期末）第24届冬季奥运会于2022年2月4日在北京市和河北省张家口市举行.现要安排5名志愿者去四个场馆参加活动，每名志愿者只能去一个场馆.且每个场馆只能安排一名志愿者，则不同的分配方法有___________个.（空格处填写数字） 【答案】120【分析】根据排列的概念和排列数公式，即可求出结果.【详解】解：从5名志愿者中选4人排列45A 120=个.9．（2022春·吉林四平·高二四平市第一高级中学校考阶段练习）方程421A 18A x x +=，的解为x =_______． 【答案】5【分析】由排列数公式直接得到关于x 的方程，解出x 的值，再代入检验得到答案. 【详解】因为421A 18A x x +=，则14,2x x +≥≥且*x ∈N ，则3x ≥且*x ∈N所以()()()()112181x x x x x x +--=-，即()()1218x x +-=，解得5x =或4x =-（舍去）．10．（2021·高二课时练习）（1）已知10A 1095m =⨯⨯⋅⋅⋅⨯，那么m =______；（2）已知2A 56n =，那么n =______； （3）已知224A 7A n n -=，那么n =______．(10m ⨯⨯-，解得m =56=，56【答案】()1!1n +-【分析】由于()!1!!n n n n ⋅=+-，然后用裂项相消的方法对其进行化简【详解】因为()()()()11!22!33!!2!1!3!2!4!3!1!!S n n n n =⋅+⋅+⋅+⋅⋅⋅+⋅=-+-+-+⋅⋅⋅++-⎡⎤⎣⎦()1!1n =+-，12．（2022秋·福建漳州·高二福建省华安县第一中学校考期中）英国数学家泰勒(1685-1731)以发现泰勒公式和泰勒级数闻名于世，由泰勒公式，我们得到1111e e 11!2!3!!(1)!n n θ=+++++++(其中e 为自然对数的底数，()()01,!12...21n n n n θ<<=⨯-⨯-⨯⨯⨯)，其拉格朗日余项是e .(1)!θ=+n R n 可以看出，右边的项用得越多，计算得到的e 的近似值也就越精确.若3(1)!n +近似地表示e 的泰勒公式的拉格朗日余项,n R n R 不超过11000时，正整数n 的最小值是_____有重复数字并且是5的倍数的五位数 【答案】660【分析】分别讨论末位为0和末位为5的情况，结合分类加法计数原理可求得结果. 【详解】若末位为0，则可组成46A 个满足题意的五位数；若末位为5，则可组成1355A A 个满足题意的五位数；∴共可组成满足题意的五位数有：413655A A A 660+=个.14．（2022春·辽宁沈阳·高二同泽高中校考阶段练习）北京时间2022年11月30日7时33分，神舟十五号航天员乘组在载人飞船与空间站组合体成功实现对接后，从飞船返回舱进入轨道舱，并与神舟十四号航天员乘组“胜利会师”，中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱．假设中国空间站要安排甲，乙，丙，丁等6名航天员开展实验，其中天和核心舱安排3人，问天实验舱安排2人，梦天实验的安排1人．若甲、乙两人不能同时在一个舱内做实验，则不同的安排方案共有______种 【答案】44【分析】首先求出总的方案种数，再求出甲乙在一起的情况，相减即可求得甲乙不在一起的情况.【详解】由题意，要安排甲，乙，丙，丁等6名航天员开展实验，其中天和核心舱安排3人，问天实验舱安排2人，梦天实验的安排1人，共有321631C C C 60=种方案；若甲乙两人同时在天和核心舱，则有121431C C C 12=种方案；若甲乙两人同时在问天实验舱，则有3141C C 4=种方案.所以甲、乙两人不能同时在一个舱内做实验，则有6012444--=种.四、解答题15．（2022·全国·高二假期作业）证明()1!!!n n n n +-=⋅，并用它来化简11!22!33!1010!⨯+⨯+⨯+⋅⋅⋅+⨯．【答案】证明见详解；11!1-【分析】利用排列数的计算公式即可证明.【详解】证明()()()1!!1!!11!!n n n n n n n n n +-=+⋅-=+-⋅=⋅，即证.11!22!33!1010!⨯+⨯+⨯+⋅⋅⋅+⨯2!1!3!2!11!10!11!1!11!1=-+-++-=-=-16．（2022·全国·高二假期作业）求证：A A A n m n m n n n m --=．【答案】证明见详解【分析】利用排列数的计算公式即可证明.【详解】左边()()=A 12321!nn n n n n =⨯-⨯-⨯⨯⨯=，右边()()()()A A 12121!m n mn n m n n n n m n m n --==⨯-⨯-⨯-+⨯-⨯⨯=，所以A A A n m n mn n n m --=，即证.17．（2022·高二课时练习）解不等式：32213P 2P 6P x x x +≤+．(1)4321A 140A x x +=； (2)1893A 4A x x -=.19．（2022秋·河北保定·高二校考阶段练习）已知2n n （n N ∈，且3n ≥）．(1)求()4f 的值；(2)若()0f n =，求n 的值． 【答案】(1)96 (2)8【分析】（1）由排列数计算公式即可求解； （2）由排列数计算公式即可求解方程. （1）解：()()3384487610432564069610f A A =⨯⨯-⨯⨯⨯=-⨯=-=；（2）解：由33210n n A A =，得()()()()221221012n n n n n n --=--，又3n ≥，*n ∈N ，所以()()22152n n -=-，即8n =，∴正整数n 为8．20．（2022春·吉林长春·高二长春十一高校考阶段练习）某学习小组有3个男生和4个女生共7人：现有7个座位连成一排，仅安排4个女生就座，恰有两个空位相邻的不同坐法共有多少种？ 【答案】480【分析】将4名女生全排列，排好后有5个空位，将3个空座位分成2、1的2组，在5个空位中任选2个，安排2组空座位，由分步计数原理计算可得答案．【详解】将4名女生全排列，有44A 种情况，排好后中间和两端共有有5个空，将3个空座位分成2个和1个的2组，在5个空位中任选2个，安排2组空座位，有25A 种情况，则有4245A A 2420480⋅=⨯=种排法．21．（2022春·上海嘉定·高二校考期中）已知一条铁路有8个车站，假设列车往返运行且每个车站均停靠上下客，记从A 车站上车到B 车站下车为1种车票（A B ≠）． (1)该铁路的客运车票有多少种？(2)为满足客运需要，在该铁路上新增了n 个车站，客运车票增加了54种，求n 的值． 【答案】(1)56 (2)3【分析】根据条件利用排列公示建立方程就可以解决.【详解】（1）铁路的客运车票有288756A =⨯=.（2）在新增了n 个车站后，共有8n +个车站，因为客运车票增加了54种，则285654n A +-=， 所以28(8)(7)110n A n n +=++=，解得3n =.【能力提升】一、单选题 1．（2022春·辽宁葫芦岛·高二校联考期中）小陈准备将新买的《尚书·礼记》、《左传》、《孟子》、《论语》、《诗经》五本书立起来放在书架上，若要求《论语》、《诗经》两本书相邻，且《尚书·礼记》放在两端，则不同的摆放方法有（ ）A ．18种B ．24种C ．36种D ．48种【答案】B【分析】先将《论语》、《诗经》两书捆绑，然后排好《尚书·礼记》，再排好剩余3个位置，最后排《论语》、《诗经》，根据分步乘法，即可求得结果.【详解】先将《论语》、《诗经》两书捆绑看作一个整体，则可以看作共4个位置. 先排《尚书·礼记》，排法种数为12A ；然后剩余3个位置全排列，排法种数为33A ；最后排好《论语》、《诗经》，两书的排法种类为22A .所以，不同的摆放方法有132232A A A 26224⋅⋅=⨯⨯=种.2．（2022春·福建福州·高二福建省福州格致中学校考阶段练习）“四书” “五经”是我国9部经典名著《大学》《论语》《中庸》《孟子》《周易》《尚书》《诗经》《礼记》《春秋》的合称．为弘扬中国传统文化，某校计划在读书节活动期间举办“四书”“五经”知识讲座，每部名著安排1次讲座，若要求《大学》《论语》相邻，但都不与《周易》相邻，则排法种数为（ ）A ．622622A A AB ．6262A AC ．622672A A A D ．622662A A A【答案】C【分析】先排除去《大学》《论语》《周易》之外的6部经典名著的讲座，将《大学》《论语》捆绑和《周易》看作两个元素，采用插空法排列，根据分步乘法计数原理，可得答案. 【详解】先排除去《大学》《论语》《周易》之外的6部经典名著的讲座， 共有66A 种排法，将《大学》《论语》看作一个元素，二者内部全排列有22A 种排法， 排完的6部经典名著的讲座后可以认为它们之间包括两头有7个空位，从7个空位中选2个，排《大学》《论语》捆绑成的一个元素和《周易》的讲座，有27A 种排法，故总共有622627A A A 种排法，3．（2022·高二单元测试）将六个数0、1、2、9、19、20将任意次序排成一行，拼成一个8位数，则产生的不同的8位数的个数是（ ）A ．498B ．516C ．534D ．5464．（2022秋·江苏南通·高二金沙中学校考阶段练习）2022年2月5日晩，在北京冬奥会短道速滑混合团体接力决赛中，中国队率先冲过终点，为中国体育代表团拿到本届奥运会首枚金牌.赛后，武大靖，任子威，曲春雨，范可欣，张雨婷5名运动员从左往右排成一排合影留念，下列结论正确的是（ ）A ．武大靖与张雨婷相邻，共有48种排法B ．范可欣与曲春雨不相邻，共有72种排法C ．任子威在范可欣的右边，共有120种排法D ．任子威不在最左边，武大靖不在最右边，共有78种排法 【答案】ABD【分析】利用分步乘法计数原理结合排列与排列数，逐项分析判断即可.【详解】解：A 项中，武大靖与张雨婷相邻，将武大靖与张雨婷排在一起有22A 种排法， 再将二人看成一个整体与其余三人全排列，有44A 种排法，由分步乘法计数原理得，共有2424A A 48=（种）排法，故选项A 正确；B 项中，范可欣与曲春雨不相邻，先将其余三人全排列，有33A 种排法， 再将范可欣与曲春雨插入其余三人形成的4个空位中，有24A 种排法， 由分步乘法计数原理得，共有3234A A =72（种）排法，故选项B 正确；C 项中，任子威在范可欣的右边，先从五个位置中选出三个位置排其余三人，有35A 种排法， 剩下两个位置排任子威、范可欣，只有1种排法，所以任子威在范可欣的右边，共有35A =60（种）排法，故选项C 错误；D 项中，武大靖，任子威，曲春雨，范可欣，张雨婷5人全排列，有55A 种排法， 任子威在最左边，有44A 种排法，武大靖在最右边，有44A 种排法， 任子威在最左边，且武大靖在最右边，有33A 种排法，所以任子威不在最左边，武大靖不在最右边，共有543543A -2A +A =78（种）排法，故选项D 正确.5．（2022秋·广东佛山·高二校考阶段练习）下列等式中，成立的有（ ）A ．11A A m m n n n --=B ．11A A m m n n m --=C ．11A A m mnn n m+=- D ．11A A A m m m n n n m -++=6．（2022春·辽宁沈阳·高二沈阳二中校考阶段练习）现有三位男生和三位女生，共六位同学，随机地站成一排，在男生甲不站两端的条件下，有且只有两位女生相邻的概率是______.【答案】35##0.6【答案】144【分析】先用捆绑法排甲乙和除丙之外的三人，再用插空法排丙，即可得答案.【详解】将甲乙两人捆绑看作一个人和除丙之外的三人全排列，共有2424A A 48=种排法，再从甲乙和除丙之外的三人形成的中间的三个空中选一个排丙，有3种排法， 故甲、乙相邻且丙不排两端的排法有483144⨯=种，8．（2022秋·江苏苏州·高二苏州中学校考期末）有一个“国际服务”项目截止到2022年7月25日还有8个名额空缺，需要分配给3个单位，则每个单位至少一个名额且各单位名额互不相同的分配方法种数是___________. 【答案】12【分析】首先确定3个单位名额互不相同的分配方式种数，再应用全排列求每种方式的分配方法数，即可得结果.【详解】各单位名额各不相同，则8个名额的分配方式有{1,2,5}，{1,3,4}两种， 对于其中任一种名额分配方式，将其分配给3个单位的方法有33A 种，所以每个单位至少一个名额且各单位名额互不相同的分配方法种数是33212A =种.9．（2022秋·江苏盐城·高二盐城市田家炳中学校考期中）若一个三位数的各位数字之和为10，则称这个三位数“十全十美数”，如208，136都是“十全十美数”，现从所有三位数中任取一个数，则这个数恰为“十全十美数”的概率是____________10．（2023·高二课时练习）有3名男生和4名女生，根据下列不同的要求，求不同的排列方法种数．(1)全体排成一行，其中甲只能在中间或者两边位置；(2)全体排成一行，其中甲不在最左边，乙不在最右边；(3)全体排成一行，其中3名男生必须排在一起；(4)全体排成一行，男、女各不相邻；(5)全体排成一行，3名男生互不相邻；(6)全体排成一行，其中甲、乙、丙三人从左至右的顺序不变；(7)排成前后二排，前排3人，后排4人；(8)全体排成一行，甲、乙两人中间必须有3人．【答案】(1)2160；(2)3720；(3)720；(4)144；(5)1440；(6)840；(7)5040；(8)720.【分析】(1)采用元素分析法，先安排甲，再排剩余的6个人；(2)采用位置分析法，先排最左边，再剔除乙在最右边的排法；(3)采用捆绑法，将男生看成一个整体，进行全排列；(4)采用插空法，先排男生，然后将女生插入其中的四个空位；(5) 采用插空法,先排女生，然后在空位中插入男生；(6) 采用定序排列，7名学生排成一行，分两步：第一步，设固定甲、乙、丙从左至右顺序的排列总数为N；第二步，对甲、乙、丙进行全排列；(7) 与无任何限制的排列相同，即7个元素的全排列；(8) 从除甲、乙以外的5人中选3人排在甲、乙中间，再将甲、乙及中间3人看作一个整体和其余2人一起共3个元素排成一排.三个项目的志愿者工作．因工作需要，每个项目仅需1名志愿者，每人至多参加1个项目，若甲不能参加A 、B 项目，乙不能参加B 、C 项目，那么共有多少种不同的选拔志愿者的方案？【答案】52【分析】根据甲乙参加与否，分类计数，可分四种情况讨论，分别计算选拔方法数量，最后汇总即可【详解】根据题意，分4种情况讨论：①甲乙都不参加志愿活动，在剩下的4人中任选3人参加即可，有34A 24=种选拔方法； ②甲参加但乙不参加志愿活动，甲只能参加C 项目，在剩下的4人中任选2人参加A 、B 项目，有24A 12=种选拔方法；③乙参加但甲不参加志愿活动，乙只能参加A 项目，在剩下的4人中任选2人参加B 、C 项目，有24A 12=种选拔方法；④甲乙都参加志愿活动，在剩下的4人中任选1人参加B 项目，有14A 4=种选拔方法.综上，则有241212452+++=.∴共有52种不同的选拔志愿者的方案12．（2022秋·江苏盐城·高二盐城市田家炳中学校考期中）现有4名男生、3名女生站成一排照相．（用数字作答）(1)两端是女生，有多少种不同的站法？(2)任意两名女生不相邻，有多少种不同的站法？(3)女生甲要在女生乙的右方(可以不相邻)，有多少种不同的站法？场仪式，其中男生倪某为领队.入场时，领队男生倪某必须排第一个，然后女生整体在男生的前面，排成一路纵队入场，共有n E 种排法；入场后，又需从男生（含男生倪某）和女生中各选一名代表到主席台服务，共有n F 种选法.（1）试求n E 和； （2）判断ln n E 和n F 的大小（N n +∈），并用数学归纳法证明.【答案】（1）2(!)n n n n n E A A n =⋅=，111(1)n n n F C C n n +=⋅=+；（2）见解析. 【详解】分析：(1)根据队里男生甲必须排第一个，然后女生整体排在男生的前面，排成一路纵队入场，可得n E ，根据从男生和女生中各选一名代表到主席台服务，可得n F ；(2)根据ln 2ln !,(1)n n E n F n n ==+，猜想2ln !(1)n n n <+，再用数学归纳法证明，第二步的证明利用分析法证明.详解：（1）()2!n n n n n E A A n =⋅=，()1111n n n F C C n n +=⋅=+.12,，由此猜想：当下面用数学归纳法证明2ln!n<时，该不等式显然成立)m>，客运车票增加了62种，问原来有多少个车站? 现在有多少个车站?1。