人教版九年级上册数学 第23章 旋转 单元测试(含答案)

第 23 章旋转单元检测（ B 卷）附答案（满分 100 分，时间40 分钟）命题人：陈锦喜单位：矿泉中学试卷命题企图 : 中考取有好多实质操作题，可是考试中有时不行能实质操作，这就需要同学们在平常着手，培育自己的实践操作能力. “旋转”既考察基着手操作有考察图形空间想象能力，本测试题是在掌握本章的知识基础长进行提高和稳固，考察数学解题过程，学生解题的切入点不一样，运用的思想方法不一样，表现出不一样的思想水平。

使不一样思想层次的考生都有表现的时机，进而有效地域分出学生不一样的数学能力。

试卷展望难度为0.6 左右。

一. 选择题 ( 每题 4 分，共 20 分)1.如图 , 过圆心 O和圆上一点 A 连一条曲线 ,将曲线OA绕 O点按同一方向连续旋转三次, 每次旋转900, 把圆分红四部分 , 则( )AA.这四部分不必定相等B.这四部分相等O·C.前一部分小于后一部分D.不可以确立2．图（ 1）中，能够经过旋转和翻折形成图案（2）的梯形切合条件为（）A．等腰梯形 ; B ．上底与两腰相等的等腰梯形 ;C．底角为 60°且上底与两腰相等的等腰梯形;D．底角为 60°的等腰梯形3．按序连结矩形各边中点所得的四边形（）A．是轴对称图形而不是中心对称图形; B．是中心对称图形而不是轴对称图形;C．既是轴对称图形又是中心对称图形; D．没有对称性4．如图，直线y= 3 x+ 3 与y轴交于点P，将它绕着点P 旋转 90?°所得的直线的分析式为（）．A． y=3x+ 3B． y=-3x+ 3 33C． y= 1x+ 3D． y=-1x+ 3 335．如图，△ ABC中，∠ B=90°，∠ C=30°， AB=1，将△ ABC?绕极点 A 旋转 180°，点 C 落在C′处，则 CC′的长为（）A．4 B ．42C．23 D ．25二、填空题（每题 4 分，共 20 分）6．以下图的五角星绕中心点旋转必定的角度后能与自己完整重合，则其旋转的角度起码为 __ ______ ．7．如图，将 Rt △ ABC 绕点 C 按顺时针方向旋转 90°到△ A?′B′ C 的地点， ?已知斜边AB=?10cm，?BC=?6cm， ?设 A?′ B?′的中点是 M，?连结 AM， ?则 AM= cm ．8．以下图，P 是等边△ ABC 内一点，△ BMC 是由△ BPA 旋转所得，则∠PBM ＝．9．如图，设 P 是等边三角形 ABC 内随意一点，△ ACP′是由△ ABP 旋转获得的，则 PA___ ___PB＋ PC(填“ >”、“<”或“＝” )．第 8题图第9题图第10题图10．如图， E、F 分别是正方形ABCD 的边 BC、CD 上一点，且BE＋ DF ＝ EF，则∠ EAF ＝____ ．三. 解答题（共 60 分）11．（ 10 分）作图 (1) 已知△ ABC和点 O，画出△ DEF，使△ DEF和△ ABC对于点 O成中心对称.(2)已知四边形 ABCD和点 O，求作四边形 A'B'C'D' ，使四边形 A'B'C'D' 和四边形 ABCD对于点 O成中心对称 .12.（ 10 分）如图是一个每边长4m 的荷花池， O 到各极点距离相等，计划在池中安装13盏灯，使夜景变得更为美丽。

人教版九年级数学上册第二十三章《旋转》单元测试题（含答案）一、单选题1．如图已知在ABC ∆中，AB AC =，90BAC ∠=，直角EPF ∠的顶点P 是BC 的中点，两边PE 、PF 分别交AB 和AC 于点E 、F ，给出以下五个结论正确的个数有（ ） ①AE CF =；②APE CPF ∠=∠；③BEP ∆≌AFP ∆；④EPF ∆是等腰直角三角形；⑤当EPF ∠在ABC ∆内绕顶点P 旋转时（点E 不与A 、B 重合），12ABC AEPF S S ∆=四边形.A ．2B ．3C ．4D ．52．如图，点A ，B ，C ，D ，O 都在方格纸的格点上，若△COD 可以由△AOB 旋转得到，则合理的旋转方式为( )A ．绕点O 顺时针旋转90°B ．绕点D 逆时针旋转60°C ．绕点O 逆时针旋转90°D ．绕点B 逆时针旋转135°3．在下列现象中：①时针转动，②电风扇叶片的转动，③转呼啦圈，④传送带上的电视机，其中是旋转的有（ ）A ．①②B ．②③C ．①④D ．③④4．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）A ．平行四边形B ．矩形C ．等腰三角形D ．正多边形5．下列四个图形中，既是轴对称图形又是中心对称图形的有（ ）个．A．0B．1C．2D．36．6．同学们曾玩过万花筒，它是由三块等宽等长的玻璃围成的，图是看到的万花筒的一个图案，图中所有的小三角形均是全等的等边三角形，其中的菱形AEFG可以看成是把菱形ABCD以点A为中心（）．A．顺时针旋转60︒得到B．顺时针旋转120︒得到C．逆时针旋转60︒得到D．逆时针旋转120︒得到7．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．8．下列图形中，既是轴对称图形又是中心对称图形的是()A．B．C．D．9．下列图案中，既不是中心对称图形也不是轴对称图形的是（）A．B．C．D．10．在下列四个汽车标志图案中，是中心对称图形的是（）A．B．C．D．第II 卷（非选择题）二、填空题11．如图，在ABCD 中，AD=3，AB=5，4sin 5A =，将ABCD 绕着点B 顺时针旋转()090θθ︒<<︒后，点A 的对应是点'A ，联结'AC ，如果'A C BC ⊥，那么cos θ的值是______．12．已知两点P(1，1)、Q(1，－1)，若点Q 固定，点P 绕点Q 旋转使线段PQ∥x 轴，则此时的点P 的坐标是_________________________；13．如图，在平面直角坐标系中，点1A 的坐标为(10)，，以1OA 为直角边作12Rt OA A ∆，并使1260A OA ∠︒＝，再以2OA 为直角边作23Rt OA A ∆，并使2360A OA ∠︒＝，再以3OA 为直角边作34Rt OA A ∆，并使3460A OA ∠︒＝…按此规律进行下去，则点2019A 的坐标为_______．14．在平面直角坐标系中，将函数y ＝2x 2＋2的图象绕坐标原点0顺时针旋转45°后，得到新曲线l.(1)如图①，已知点A(-1，a)，B(b ，10)在函数y ＝2x 2＋2的图象上，若A’、B’是A 、B 旋转后的对应点，连结OA’，OB’，则S △OA’B’=____.(2)如图②，曲线与直线322y =相交于点M 、N ，则S △OMN 为_________.15．如图，在△ABC 中，∠ABC=112°，将△ABC 绕着点B 顺时针旋转一定的角度后得到△DBE （点A 与点D 对应），当A 、B 、E 三点在同一直线上时，可得∠DBC 的度数为_______.16．如图1是实验室中的一种摆动装置，BC 在地面上，支架ABC 是底边为BC 的等腰直角三角形，摆动臂AD 可绕点A 旋转，摆动臂DM 可绕点D 旋转，30AD = ，10DM =.（1）在旋转过程中，当A D M ，，为同一直角三角形的顶点时，AM 的长为______________.（2）若摆动臂AD 顺时针旋转90°，点D 的位置由ABC 外的点1D 转到其内的点2D 处，连结12D D ，如图2，此时2135AD C ∠=︒，260CD =，2BD 的长为______________.17．如图，在△ABC 中，∠BAC=45°，AB=4cm ，将△ABC 绕点B 按逆时针方向旋转45°后得到△A′BC′，则阴影部分的面积为 ___________．18．如图，在△ABC 中，AB=2，BC=3.6，∠B=60°，将△ABC 绕点A 按顺时针旋转一定角度得到△ADE ，当点B 的对应点D 恰好落在BC 边上时，则CD 的长为______．三、解答题19．已知正方形ABCD ，点P 是其内部一点.（1）如图1，点P 在边AD 的垂直平分线l 上，将DAP ∆绕点D 逆时针旋转，得到11DA P ∆，当点1P 落在DC 上时，恰好点1A 落在直线l 上，求ADP 的度数；（2）如图2，点P 在对角线AC 上，连接PB ，若将线段BP 绕点P 逆时针旋转90︒后得到线段1B P ，试问点1B 是否在直线CD 上，请给出结论，并说明理由；（3）如图3，若135APB ∠=︒，设PA a =，PD b =，PC c =，请写出a 、b 、c 这三条线段长之间满足的数量关系是____________.20．（1）问题发现如图①，△ABC 和△AED 都是等腰直角三角形，∠BAC=∠EAD=90°，点B 在线段AE 上，点C 在线段AD 上，请直接写出线段BE 与线段CD 的数量关系： ；（2）操作探究如图②，将图①中的△ABC 绕点A 顺时针旋转，旋转角为α（0＜α＜360），请判断线段BE 与线段CD 的数量关系，并说明理由．21．如图，四边形ABCD 是正方形，△ADF 绕着点A 顺时旋转90°得到△ABE ，若AF ＝4，AB ＝7．（1）求DE 的长度；（2）指出BE 与DF 的关系如何？并说明由．22．如图，已知：如图点()4,0A ，点B 在y 轴正半轴上，且5AB =，将线段BA 绕点A 沿顺时针旋转90，设点B 旋转后的对应点是点1B ，求点1B 的坐标．23．在△ABC 中，∠ACB =90°，AC =BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E ．（1）当直线MN 绕点C 旋转到图1的位置时，求证：DE =AD +BE ；（2）当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，请写出新的结论并说明理由．24．如图，在正方形网格中，点A 、B 、C 、M 、N 都在格点上．（1）作△ABC关于直线MN对称的图形△A′B′C′．（2）若网格中最小正方形的边长为1，求△ABC的面积．25．（1）如图1，已知正方形ABCD，点M和N分别是边BC，CD上的点，且BM=CN，连接AM和BN，交于点P．猜想AM与BN的位置关系，并证明你的结论；（2）如图2，将图（1）中的△APB绕着点B逆时针旋转90º，得到△A′P′B，延长A′P′交AP 于点E，试判断四边形BPEP′的形状，并说明理由．26．下列图形是中心对称图形吗？如果是中心对称图形，在图中用点O标出对称中心．27．已知：如图所示，△ABC为任意三角形，若将△ABC绕点C顺时针旋转180°得到△DEC．（1）试猜想AE与BD有何关系？并且直接写出答案．（2）若△ABC的面积为4cm2，求四边形ABDE的面积；（3）请给△ABC 添加条件，使旋转得到的四边形ABDE 为矩形，并说明理由参考答案1．D2．C3．A4．B5．B6．D7．B8．D9．C10．B11．72512．（－1，－1）或（3，－1）13．()201720172,23- 14．99415．44° 16．202或1010； 306．17．42【详解】 解： AC 与BA′相交于D ，如图，∵△ABC 绕点B 按逆时针方向旋转45°后得到△A′BC′，∴∠ABA′=45°，BA′BA=4，△ABC ≌△A′BC′，∴S △ABC =S △A′BC′，∵S 四边形AA′C′B =S △ABC +S 阴影部分=S △A′BC′+S △ABA′，∴S 阴影部分=S △ABA′，∵∠BAC=45°，∴△ADB 为等腰直角三角形，∴∠ADB=90°，AD=222， ∴S △ABA′=12AD•BA′=12×2×2（cm 2）， ∴S 阴影部分2cm 2．故答案为：42．18．1.6【详解】由旋转的性质可得：AD=AB ，∵∠B=60°，∴△ABD 是等边三角形，∴BD=AB ，∵AB=2，BC=3.6，∴CD=BC-BD=3.6-2=1.6．故答案为1.6．19．（1）30；（2）点1B 在直线CD 上，理由见解析；（3）222320a b c -+= 连接1AA ，∵点1A 在边AD 的垂直平分线l 上，∴11AA DA =.又∵AD DA =，∴1AA D ∆是等边三角形，∴160ADA ∠=︒，∴1160PDP ADA ∠=∠=︒，∴19030ADP PDP ∠=︒-∠=︒.（2）点1B 在直线CD 上.证明如下：作PQ PB ⊥交CD 于点Q ，过点P 作//EF AD 交AB 于点E 交CD 于点F . ∴90BPQ BEP PFQ ∠=∠=∠=︒，∴90EBP EPB PQF FPQ ∠+∠=∠+∠=，90EPB FPQ ∠+∠=∴=EBP FPQ ∠∠又∵P 在正方形对角线AC 上，∴∠EAP=∠APE=45°∴AE EP =，∵AE EB EP PE +=+，∴BE FP =，∴()BEP PFQ ASA ∆≅∆，∴1BP PQ B P ==.即将线段BP 绕点P 8逆时针旋转90︒后得到线段1B P ，点1B 在直线CD 上.（3）如图，将△ABP 绕点A 逆时针旋转90°得到△AMD，由题意可知：∠APB=∠AAMD=135°，DM=BP,AP=AM=a ，∠PAM=90°∴∠AMP=45°∴∠PMD=90°∴在Rt△APM 中，22222PM AM AP a =+=在Rt△PMD 中，222PM DM PD +=∴2222DM b a =-将△ABP 绕点B 顺时针旋转90°得到△BNC，同理可证在Rt△PNC 中，22222PN PC NC c a =-=-在Rt△BPN 中，222PN BP BN =+ ∴2222==22PN c a BP - 所以可得：2222-2=2c a b a - 整理得：222320a b c -+=.20．（1）BE=CD ；（2）BE=CD ；证明见解析.【详解】解：（1）BE=CD ，理由如下；∵△ABC 和△AED 都是等腰直角三角形，∠BAC=∠EAD=90°， ∴AB=AC ，AE=AD ，∴AE ﹣AB=AD ﹣AC ，∴BE=CD ；故答案为：BE=CD ．（2）∵△ABC 和△AED 都是等腰直角三角形，∠BAC=∠EAD=90°，∴AB=AC ，AE=AD ，由旋转的性质得，∠BAE=∠CAD ，在△BAE 与△CAD 中，，∴△BAE ≌△CAD （SAS ）∴BE=CD ．21．（1）3；（2）BE ＝DF ，BE ⊥DF ．【详解】解：（1）∵△ADF 按顺时针方向旋转一定角度后得到△ABE ，∴AE ＝AF ＝4，AD ＝AB ＝7，∴DE ＝AD ﹣AE ＝7﹣4＝3；（2）BE 、DF 的关系为：BE ＝DF ，BE ⊥DF ．理由如下：∵△ADF 按顺时针方向旋转一定角度后得到△ABE ，∴△ABE ≌△ADF ，∴BE ＝DF ，∠ABE ＝∠ADF ，∵∠ADF +∠F ＝180°﹣90°＝90°， ∴∠ABE +∠F ＝90°， ∴BE ⊥DF ，∴BE 、DF 的关系为：BE ＝DF ，BE ⊥DF ．22．1B 点的坐标为()7,4．【详解】解：如图，作1B C x ⊥轴于C ，∵4OA =，5AB =，∴22543OB -=，∵线段BA 绕点A 沿逆时针旋转90得1A B ，∴1BA A B =，且190BA B ∠=，∴190BAO B AC ∠+∠=而90BAO ABO ∠+∠=，∴1ABO B AC ∠=∠，在ABO 和1B AC 中111AOB B CA ABO B AC AB B A ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴1ABO B AC ≅，∴3AC OB ==，14B C OA ==，∴7OC OA AC =+=，∴1B 点的坐标为()7,4．23．（1）证明见解析；（2）DE=AD-BE试题解析：证明：（1）∵AD ⊥DE ，BE ⊥DE ，∴∠ADC =∠BEC =90°，∵∠ACB =90°，∴∠ACD +∠BCE =90°，∠DAC +∠ACD =90°，∴∠DAC =∠BCE ，在△ADC 和△CEB 中CDA BEC DAC ECB AC BC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADC ≌△CEB （AAS ），∴AD=CE ，CD=BE ，∵DC+CE=DE ，∴AD+BE=DE ．（2）DE=AD-BE ，理由：∵BE ⊥EC ，AD ⊥CE ，∴∠EBC+∠ECB=90°，∵∠ACB=90°，∴∠ECB+∠ACE=90°，∴∠ACD=∠EBC，在△ADC和△CEB中，ACD CBEADC BECAC BC∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADC≌△CEB（AAS），∴AD=CE，CD=BE，∴DE=EC-CD=AD-BE．24．（1）见解析；（2）3．【详解】解：（1）如图，△A′B′C′为所作；（2）△ABC的面积=12×3×2=3．25．（1）AM⊥BN，证明见解析；（2）四边形BPEP′是正方形，理由见解析.【详解】（1）AM⊥BN证明：∵四边形ABCD是正方形，∴AB=BC，∠ABM=∠BCN=90°∵BM=CN，∴△ABM≌△BCN∴∠BAM=∠CBN∴∠ABN+∠BAM=90°，∴∠APB=90°∴AM⊥BN．（2）四边形BPEP′是正方形.△A′P′B是△APB绕着点B逆时针旋转90º所得，∴BP= BP′,∠P′BP=90º.又由（1）结论可知∠APB=∠A′P′B=90°，∴∠BP′E=90°.所以四边形BPEP′是矩形.又因为BP= BP′,所以四边形BPEP′是正方形.26．图形1，图形3，图形4，图形5，图形8为中心对称图形，其对称中心为图形中的点O．【详解】这些图形中：图形1，图形3，图形4，图形5，图形8为中心对称图形，其对称中心为图形中的点O．27．（1）AE∥BD，且AE=BD．（2）16；（3）当∠ACB=60°时，四边形ABFE为矩形．【解析】试题分析：（1）易证四边形ABDE是平行四边形，根据平行四边形的性质即可求解；（2）根据平行四边形的性质：平行四边形的对角线互相平分，即可得到平行四边形的面积是△ABC的面积的四倍，据此即可求解；（3）四边形ABDE是平行四边形，只要有条件：对角线相等即可得到四边形ABDE是矩形．试题解析：（1）AE∥BD，且AE=BD；（2）四边形ABDE的面积是：4×4=16；（3）AC=BC．理由是：∵AC=CD，BC=CE，∴四边形ABDE是平行四边形．∵AC=BC，∴平行四边形ABDE是矩形．考点：1．旋转的性质；2．矩形的判定。

人教版九年级数学上册第23章旋转单元练习卷含答案(1)一、选择题1. 下列几个图形是国际通用的交通标志，其中不是中心对称图形的是（）A. B. C. D.2．在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转．下列图形中不能由一个图形通过旋转而构成的是( )A B C D3．下列运动形式属于旋转的是（）A．在空中上升的氢气球B．飞驰的火车C．时钟上钟摆的摆动D．运动员掷出的标枪4．如图是扬州“三菱”电梯的标志，它可以看作是由菱形通过旋转得到的，每次旋转了（）A．60°B．90°C．120°D．150°5. 若点P(－m，m－3)关于原点对称的点是第二象限内的点，则m满足()A. m＞3B. 0＜m≤3C. m＜0D. m＜0或m＞36．如图，是用围棋子摆出的图案(围棋子的位置用有序数对表示，如点A在(5，1))，如果再摆一黑一白两枚棋子，使9枚棋子组成的图案既是轴对称图形又是中心对称图形，则下列摆放正确的是( )A．黑(3，3)，白(3，1) B．黑(3，1)，白(3，3)C．黑(1，5)，白(5，5) D．黑(3，2)，白(3，3)7．如图，△DEF是由△ABC绕着某点旋转得到的，则这点的坐标是（）A．（1，1）B．（2，0）C．（0，1）D．（3，1）8. 如图，△ACD和△AEB都是等腰直角三角形，∠CAD＝∠EAB＝90°.四边形ABCD是平行四边形，下列结论中错误的是()A. △ACE以点A为旋转中心，逆时针旋转90°后与△ADB重合B.△ACB以点A为旋转中心，顺时针旋转270°后与△DAC重合C. 沿AE所在直线折叠后，△ACE与△ADE重合D. 沿AD所在直线折叠后，△ADB与△ADE重合9．如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转到ABF的位置，若四边形AECF的面积为25，DE=2，则AE的长为（）A．7 B．6 C．D．510．已知等边△ABC的边长为4，点P是边BC上的动点，将△ABP绕点A逆时针旋转60°得到△ACQ，点D是AC边的中点，连接DQ，则DQ的最小值是（）A．B．C．2 D．不能确定二、填空题11. 钟表分针的运动可以看作是一种旋转现象，经过40分钟分针旋转了°. 12．如图，在△ABC中，∠C＝90°，∠BAC＝70°，将△ABC绕点A顺时针旋转70°，点B，C旋转后的对应点分别是点D和E，连接BD，则∠BDE的度数是．13．如图，线段AB的端点A、B分别在x轴和y轴上，且A（2，0），B（0，4），将线段AB绕坐标原点O逆时针旋转90°得线段A'B'，设线段AB'的中点为C，则点C的坐标是．14．如图，大圆的面积为4π，大圆的两条直径互相垂直，则图中阴影部分的面积的和为____．15. 如图，△ABC绕点A逆时针旋转30°后到△A′B′C′的位置，若∠B′＝45°，∠C′＝60°，则∠B′AC＝.16．如图，在直角坐标系中，已知点P0的坐标为（1，0），将线段OP0按照逆时针方向旋转45°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按照逆时针方向旋转45°，长度伸长为OP1的2倍，得到线段OP2；如此下去，得到线段OP3，OP4，…，OP n（n为正整数），则点P8的坐标为．17.如图，在△ABC中、∠C＝90°，AC＝3，BC＝4，点O是BC的中点，将△ABC绕点O 旋转得△A'B'C',则在旋转过程中点A，C'两点间的最大距离是__________.18．如图，正方形ABCD，将正方形AEFG绕点A旋转，连接DF，点M是DF的中点，连接CM，若AB＝4，AE＝1，则线段CM的最大值为．三、解答题19．如图，△ABC为等边三角形，△AP′B旋转后能与△APC重合，那么：（1）指出旋转中心；（2）求旋转角的度数；（3）求∠PAP′的度数．20．在平面直角坐标系中，△ABC的位置如图所示（每个小方格都是边长1个单位长度的正方形）．（1）将△ABC沿x轴方向向左平移6个单位，画出平移后得到的△A1B1C1；（2）将△ABC绕着点A顺时针旋转90°，画出旋转后得到的△AB2C2；直接写出点B2的坐标；（3）作出△ABC关于原点O成中心对称的△A3B3C3，并直接写出B3的坐标．21.如图，在平面直角坐标系中，O为坐标原点，每个小方格的边长为1个单位长度，在第二象限内有横、纵坐标均为整数的A，B两点，点B(－2，3)，点A的横坐标为－2，且OA ＝ 5.(1)直接写出A点的坐标，并连接AB，AO，BO；(2)画出△OAB关于点O成中心对称的图形△OA1B1，并写出点A1，B1的坐标(点A1，B1的对应点分别为A，B)；(3)将△OAB逆时针旋转90°得到△O1A2B2，画出△O1A2B2.22．如图，在正方形ABCD中，E为CD上一点，F为BC延长线上一点，CE＝CF.(1)△DCF可以看成是△BCE绕点C旋转某个角度得到的吗？(2)若∠CEB＝60°，求∠EFD的度数．23．如图①，△ABC和△AEF都为等腰直角三角形，∠ACB＝∠AEF＝90°，连接EC、BF，点D为BF的中点，连接CD．(1)如图①，当点E落在AB边上时，请判断线段EC与DC的数量关系，并证明你的结论；(2)将△AEF绕点A顺时针旋转n°（n＜180），如图②，请判断线段EC与DC的数量关系，并证明你的结论；(3)若AC＝2，点P为BC中点，动点Q满足PQ＝，如图③，将线段AQ绕点A逆时针旋转90°到线段AM，连PM，则线段PM的最小值为.图①图②人教新版九年级数学上第23章旋转单元练习试题含详细答案一．选择题（共10小题）1．下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．2．五角星可以看成由一个四边形旋转若干次而生成的，则每次旋转的度数可以是（）A．36°B．60°C．72°D．90°3．如图，△ODC是由△OAB绕点O顺时针旋转50°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为130°，则∠C的度数是（）A．25°B．30°C．35°D．40°4．下列各图中，既可经过平移，又可经过旋转，由图形①得到图形②的是（）A．B．C．D．5．如图，将△ABC绕点A逆时针旋转110°，得到△ADE，若点D落在线段BC的延长线上，则∠B大小为（）A．30°B．35°C．40°D．45°6．在俄罗斯方块游戏中，若某行被小方格块填满，则该行中的所有小方格会自动消失．现在游戏机屏幕下面三行已拼成如图所示的图案，屏幕上方又出现一小方格块正向下运动，为了使屏幕下面三行中的小方格都自动消失，你可以将图形进行以下的操作（）A．先逆时针旋转90°，再向左平移B．先顺时针旋转90°，再向左平移C．先逆时针旋转90°，再向右平移D．先顺时针旋转90°，再向右平移7．如图，香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合，则n 的最小值为（）A．45 B．60 C．72 D．1448．在平面直角坐标系中，点A的坐标是（1，3），将点A绕原点O顺时针旋转90°得到点A′，则点A′的坐标是（）A．（﹣3，1）B．（3，﹣1）C．（﹣1，3）D．（1，﹣3）9．如图，在平面直角坐标系xOy中，点A从（3，4）出发，绕点O顺时针旋转一周，则点A不经过（）A．点M B．点N C．点P D．点Q10．如图，△ABC与△A′B′C′关于点O成中心对称，则下列结论不成立的是（）A．点A与点A′是对称点B．BO＝B′OC．AB∥A′B′D．∠ACB＝∠C′A′B′二．填空题（共9小题）11．如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连结AA′，若∠1＝20°，则∠B＝度．12．如图，正方形ABCD与正三角形AEF的顶点A重合，将△AEF绕其顶点A旋转，在旋转过程中，当BE＝DF时，∠BAE的大小是．13．点A（﹣2，3）关于原点对称的点的坐标是．14．如图，点A、B、C、D都在方格纸的格点上，若△AOB绕点O按逆时针方向旋转到△COD的位置，则旋转角为．15．如图，在平面直角坐标系xOy中，直线y＝x经过点A，作AB⊥x轴于点B，将△ABO 绕点B逆时针旋转60°得到△CBD，若点B的坐标为（2，0），则点C的坐标为．16．如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A′B′C，M 是BC的中点，P是A′B′的中点，连接PM，若BC＝2，∠BAC＝30°，则线段PM的最大值是．17．在△ABC中，∠C＝90°，AC＝BC，将△ABC绕点A按顺时针方向旋转60°到△AB′C′的位置，连结C′B、BB′，则∠BB′C′＝．18．在平面直角坐标系中，已知点A（3，0），B（0，4），将△BOA绕点A按顺时针方向旋转得△CDA，使点B在直线CD上，连接OD交AB于点M，直线CD的解析式为．19．如图，△ABC是边长为12的等边三角形，D是BC的中点，E是直线AD上的一个动点，连接EC，将线段EC绕点C逆时针旋转60°得到FC，连接DF．则在点E的运动过程中，DF的最小值是．三．解答题（共6小题）20．如图，在4×4的方格纸中，△ABC的三个顶点都在格点上．（1）在图1中，画出一个与△ABC成中心对称的格点三角形；（2）在图2中，画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形；（3）在图3中，画出△ABC绕着点C按顺时针方向旋转90°后的三角形．21．在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，请解答下列问题：（1）作出△ABC向左平移4个单位长度后得到的△A1B1C1，并写出点C1的坐标；（2）作出△ABC关于原点O对称的△A2B2C2，并写出点C2的坐标；（3）已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为（﹣4，﹣2），请直接写出直线l的函数解析式．22．如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，2）请解答下列问题：（1）画出△ABC关于y轴对称的△A1B1C1，并写出A1的坐标．（2）画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2，并写出A2的坐标．（3）画出△A2B2C2关于原点O成中心对称的△A3B3C3，并写出A3的坐标．23．在平面直角坐标系中，△ABC三个顶点的坐标分别为A（2，3），B（1，1），C（5，1）．（1）把△ABC平移后，其中点A移到点A1（4，5），画出平移后得到的△A1B1C1；（2）把△A1B1C1绕点A1按逆时针方向旋转90°，画出旋转后的△A2B2C2．24．将矩形ABCD绕点A顺时针旋转α（0°＜α＜360°），得到矩形AEFG．（1）如图，当点E在BD上时．求证：FD＝CD；（2）当α为何值时，GC＝GB？画出图形，并说明理由．25．如图，已知△ABC中，AB＝AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F．（1）求证：△AEC≌△ADB；（2）若AB＝2，∠BAC＝45°，当四边形ADFC是菱形时，求BF的长．参考答案一．选择题（共10小题）1．解：A、是轴对称图形，不是中心对称图形，故此选项错误；B、是轴对称图形，不是中心对称图形，故此选项错误；C、不是轴对称图形，是中心对称图形，故此选项错误；D、是轴对称图形，也是中心对称图形，故此选项正确．故选：D．2．解：根据旋转的性质可知，每次旋转的度数可以是360°÷5＝72°或72°的倍数．故选C．3．解：∵∠AOC的度数为130°，∠AOD＝∠BOC＝50°，∴∠AOB＝130°﹣50°＝80°，∵△AOD中，AO＝DO，∴∠A＝（180°﹣50°）＝65°，∴△ABO中，∠B＝180°﹣80°﹣65°＝35°，由旋转可得，∠C＝∠B＝35°，故选：C．4．解：A、B、C中只能由旋转得到，不能由平移得到，只有D可经过平移，又可经过旋转得到．故选：D．5．解：∵△ABC绕点A逆时针旋转110°，得到△ADE∴AB＝AD，∠BAD＝110°由三角形内角和∠B＝故选：B．6．解：屏幕上方又出现一小方格块正向下运动，为了使屏幕下面三行中的小方格都自动消失，可以先逆时针旋转90°，再向左平移．故选：A．7．解：该图形被平分成五部分，旋转72°的整数倍，就可以与自身重合，故n的最小值为72．故选：C．8．解：如图所示，由旋转可得：∠AOA'＝∠BOC＝90°，AO＝A'O，∴∠AOB＝∠A'OC，而∠ABO＝∠A'CO＝90°，∴△AOB≌△A'OC，∴A'C＝AB＝1，CO＝BO＝3，∴点A'的坐标为（3，﹣1），故选：B．9．解：由图形可得：OA＝，OM＝，ON＝，OP＝，OQ＝5，所以点A从（3，4）出发，绕点O顺时针旋转一周，则点A不经过P点，故选：C．10．解：观察图形可知，A、点A与点A′是对称点，故本选项正确；B、BO＝B′O，故本选项正确；C、AB∥A′B′，故本选项正确；D、∠ACB＝∠A′C′B′，故本选项错误．故选：D．二．填空题（共9小题）11．解：∵Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，∴∠ACA′＝90°，CA＝CA′，∠B＝∠CB′A′，∴△CAA′为等腰直角三角形，∴∠CAA′＝45°，∵∠CB′A′＝∠B′AC+∠1＝45°+20°＝65°，∴∠B＝65°．故答案为65．12．解：∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，∵△AEF是等边三角形，∴AE＝AF，∠EAF＝60°，分两种情况：①如图，当正△AEF在正方形ABCD内部时，在△ABE和△ADF中，∴△ABE≌△ADF（SSS），∴∠BAE＝∠DAF＝（90°﹣60°）＝15°②如图，当正△AEF在正方形ABCD外部时，在△ABE和△ADF中，∴△ABE≌△ADF（SSS），∴∠BAE＝∠DAF＝（360°﹣90°+60°）＝165°故答案为：15°或165°．13．解：根据两个点关于原点对称，∴点P（﹣2，3）关于原点对称的点的坐标是（2，﹣3）；故答案为（2，﹣3）．14．解：∵△AOB绕点O按逆时针方向旋转到△COD的位置，∴对应边OB、OD的夹角∠BOD即为旋转角，∴旋转的角度为90°．故答案为：90°．15．解：过点C作CE⊥x轴于点E，∵OB＝2，AB⊥x轴，点A在直线y＝x上，∴AB＝2，OA＝＝4，∴RT△ABO中，tan∠AOB＝＝，∴∠AOB＝60°，又∵△CBD是由△ABO绕点B逆时针旋转60°得到，∴∠D＝∠AOB＝∠OBD＝60°，AO＝CD＝4，∴△OBD是等边三角形，∴DO＝OB＝2，∠DOB＝∠COE＝60°，∴CO＝CD﹣DO＝2，在RT△COE中，OE＝CO•cos∠COE＝2×＝1，CE＝CO•sin∠COE＝2×＝，∴点C的坐标为（﹣1，），故答案为：（﹣1，）．16．解：如图连接PC．在Rt△ABC中，∵∠A＝30°，BC＝2，∴AB＝4，根据旋转不变性可知，A′B′＝AB＝4，∴A′P＝PB′，∴PC＝A′B′＝2，∵CM＝BM＝1，又∵PM≤PC+CM，即PM≤3，∴PM的最大值为3（此时P、C、M共线）．故答案为：3．17．解：∵∠C＝90°，AC＝BC，∴∠ABC＝∠BAC＝45°，∵将△ABC绕点A按顺时针方向旋转60°到△AB′C′的位置，∴∠AB′C′＝∠ABC＝45°，∠BAB′＝60°，AB′＝AB，∴AB′＝B′B＝BA，∴∠AB′B＝60°，∴∠BB′C′＝∠AB′B﹣∠AB′C′＝60°﹣45°＝15°，故答案为：15°．18．解：∵△BOA绕点A按顺时针方向旋转得△CDA，∴△BOA≌△CDA，∴AB＝AC，OA＝AD，∵B、D、C共线，AD⊥BC，∴BD＝CD＝OB，∵OA＝AD，BO＝CD＝BD，∴OD⊥AB，设直线AB解析式为y＝kx+b，把A与B坐标代入得：，解得：，∴直线AB解析式为y＝﹣x+4，∴直线OD解析式为y＝x，联立得：，解得：，即M（，），∵M为线段OD的中点，∴D（，），设直线CD解析式为y＝mx+n，把B与D坐标代入得：，解得：m＝﹣，n＝4，则直线CD解析式为y＝﹣x+4．故答案为：y＝﹣．19．解：取线段AC的中点G，连接EG，如图所示．∵△ABC为等边三角形，且AD为△ABC的对称轴，∴CD＝CG＝AB＝6，∠ACD＝60°，∵∠ECF＝60°，∴∠FCD＝∠ECG．在△FCD和△ECG中，，∴△FCD≌△ECG（SAS），∴DF＝GE．当EG∥BC时，EG最小，∵点G为AC的中点，∴此时EG＝DF＝CD＝BC＝3．故答案为3．三．解答题（共6小题）20．解：（1）如图所示，△DCE为所求作（2）如图所示，△ACD为所求作（3）如图所示△ECD为所求作21．解：（1）如图，△A1B1C1为所作，C1（﹣1，2）；（2）如图，△A2B2C2为所作，C2（﹣3，﹣2）；（3）因为A的坐标为（2，4），A3的坐标为（﹣4，﹣2），所以直线l的函数解析式为y＝﹣x，22．解：（1）画出△ABC关于y轴对称的△A1B1C1，如图所示，此时A1的坐标为（﹣2，2）；（2）画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2，如图所示，此时A2的坐标为（4，0）；（3）画出△A2B2C2关于原点O成中心对称的△A3B3C3，如图所示，此时A3的坐标为（﹣4，0）．23．解：（1）如图，△A1B1C1即为所求；（2）如图，△A2B2C2即为所求．24．解：（1）由旋转可得，AE＝AB，∠AEF＝∠ABC＝∠DAB＝90°，EF＝BC＝AD，∴∠AEB＝∠ABE，又∵∠ABE+∠EDA＝90°＝∠AEB+∠DEF，∴∠EDA＝∠DEF，又∵DE＝ED，∴△AED≌△FDE（SAS），∴DF＝AE，又∵AE＝AB＝CD，∴CD＝DF；（2）如图，当GB＝GC时，点G在BC的垂直平分线上，分两种情况讨论：①当点G在AD右侧时，取BC的中点H，连接GH交AD于M，∵GC＝GB，∴GH⊥BC，∴四边形ABHM是矩形，∴AM＝BH＝AD＝AG，∴GM垂直平分AD，∴GD＝GA＝DA，∴△ADG是等边三角形，∴∠DAG＝60°，∴旋转角α＝60°；②当点G在AD左侧时，同理可得△ADG是等边三角形，∴∠DAG＝60°，∴旋转角α＝360°﹣60°＝300°．25．解：（1）由旋转的性质得：△ABC≌△ADE，且AB＝AC，∴AE＝AD，AC＝AB，∠BAC＝∠DAE，∴∠BAC+∠BAE＝∠DAE+∠BAE，即∠CAE＝∠DAB，在△AEC和△ADB中，，∴△AEC ≌△ADB （SAS ）；（2）∵四边形ADFC 是菱形，且∠BAC ＝45°，∴∠DBA ＝∠BAC ＝45°，由（1）得：AB ＝AD ，∴∠DBA ＝∠BDA ＝45°，∴△ABD 为直角边为2的等腰直角三角形，∴BD 2＝2AB 2，即BD ＝2，∴AD ＝DF ＝FC ＝AC ＝AB ＝2，∴BF ＝BD ﹣DF ＝2﹣2．人教版九年级上册第二十三章旋转单元测试（含答案）(2)一、选择题：（每小题3分共30分）1．如图，在等腰直角△ABC 中，∠C ＝90°，将△ABC 绕顶点 A 逆时针旋转 80°后得△AB′C′，则∠CAB′的度数为（ ）A ．45°B ．80°C ．125°D ．130°2．如图，把ABC ∆绕着点A 逆时针旋转20︒得到ADE ∆，30BAC ∠=︒，则BAE ∠的度数为（ ）A ．10︒B ．20︒C ．30°D ．50︒3．图中，不能由一个基本图形通过旋转而得到的是( )A．B．C．D．4．在以下几种生活现象中，不属于旋转的是()A．下雪时，雪花在天空中自由飘落B．钟摆左右不停地摆动C．时钟上秒针的转动D．电风扇转动的扇叶5．下列图形中，既是中心对称图形又是轴对称图形的是（）A. B. C. D.6．下列图形中，既是轴对称图形，又是中心对称图形的是（）A.等边三角形B.等腰直角三角形C.平行四边形D.菱形7．如图，将绕点逆时针旋转一定的角度，得到，且.若，，则的大小为（）A. B. C. D.8．如图①，在△AOB 中，∠AOB=90°，OA=3，OB=4,AB=5．将△AOB 沿x 轴依次绕点A、B、O 顺时针旋转，分别得到图②、图③、…，则旋转得到的图⑩的直角顶点的坐标为（）A.（30，0） B.（32，0） C.（34，0） D.（36，0）△绕点B顺时针旋转60 得到DBE，点C的对应点E落在AB的延长9．如图，将ABC线上，连接,AD AC 与DE 相交于点F .则下列结论不一定正确的是（ ）A ．60ABD CBE ︒∠=∠=B ．ADB △是等边三角形C ．BC DE ⊥D ．60EFC ︒∠=10．在等边△ABC 中，D 是边AC 上一点，连接BD ，将△BCD 绕点B 逆时针旋转60°，得到△BAE ，连接ED ，若BC=5，BD=4，则以下四个结论中：①△BDE 是等边三角形； ②AE ∥BC ； ③△ADE 的周长是9； ④∠ADE=∠BDC ．其中正确的序号是（ ）A ．②③④B ．①②④C ．①②③D ．①③④二、填空题：（每小题3分共18分）11．在平面直角坐标系中，点(45)P -，与点Ｑ(4,1m -+)关于原点对称，那么m =_____；12．如图，等腰△ABC 中，∠BAC =120°，点D 在边BC 上，等腰△ADE 绕点A 顺时针旋转30°后，点D 落在边AB 上，点E 落在边AC 上，若AE =2cm ，则四边形ABDE 的面积是__________．13．如图，在ΔABC 中，AB=8，AC=6，∠BAC=30°，将ΔABC 绕点A 逆时针旋转60°得到△AB 1C 1，连接BC 1，则BC 1的长为________.14．如图，两块相同的三角板完全重合在一起，30,10A AC ∠==，把上面一块绕直角顶点B 逆时针旋转到''A BC ∆的位置，点'C 在AC 上，''A C 与AB 相交于点D ，则'BC =______．15．如图，在矩形ABCD 中，3AD =，将矩形ABCD 绕点A 逆时针旋转，得到矩形AEFG ，点B 的对应点E 落在CD 上，且60DAG ∠=︒，若EC =AB =__．16．如图，点D 是等边ABC △内部一点，1BD =，2DC =，AD =ADB ∠的度数为=________°．三、解答题：（共72分）17．如图，已知△ABC 的顶点A ，B ，C 的坐标分别是A （-1，-1），B （-4，-3），C （-4，-1）．（1）作出△ABC 关于原点O 中心对称的图形△A ’B ’C ’；（2）将△ABC 绕原点O 按顺时针方向旋转90°后得到△A 1B 1C 1，画出△A 1B 1C 1，并写出点A 1的坐标．18．已知，P 为等边三角形内一点，且BP=3，PC=4，将BP 绕点B 顺时针旋转60°至BP′的位置．（1）试判断△BPP′的形状，并说明理由；（2）若∠BPC=150°，求PA 的长度．19．如图，在平面直角坐标系中，直线:3l y x =-+与x 轴、y 轴分别交于点A ,B ，将点B 绕坐标原点O 顺时针旋转60︒得点C ，解答下列问题:（1）求出点C 的坐标，并判断点C 是否在直线l 上；（2）若点P 在x 轴上，坐标平面内是否存在点Q ，使得以P 、C 、Q 、A 为顶点的四边形是菱形？若存在，请直接写出Q 点坐标；若不存在，请说明理由．20．在Rt△ABC中，∠ACB=90°，，点D是斜边AB上一动点（点D与点A、B 不重合），连接CD，将CD绕点C顺时针旋转90°得到CE，连接AE，DE．（1）求△ADE的周长的最小值；（2）若CD=4，求AE的长度．21．四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如图所示，如果AF=3，AB=7，求(1)指出旋转中心和旋转角度；(2)求DE的长度；(3)BE与DF的位置关系如何？请说明理由．22．如图所示：已知∠ABC＝120°，作等边△ACD，将△ACD旋转60°，得到△CDE，AB＝3，BC＝2，求BD和∠ABD．23．如图，把一副三角板如图①放置，其中，∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6cm，DC=7cm．把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图②）．(1)求∠OFE1的度数；(2)求线段AD1的长．24．如图，在正方形ABCD 中，点M 、N 是BC 、CD 边上的点，连接AM 、BN ，若BM=CN（1）求证：AM ⊥BN（2）将线段AM 绕M 顺时针旋转90°得到线段ME ，连接NE ，试说明：四边形BMEN 是平行四边形；（3）将△ABM 绕A 逆时针旋转90°得到△ADF ，连接EF ，当1 BM BC n时，请求出四边形四边形ABCD AMEFS S 的值。

人教版九年级数学上第23章旋转单元测试卷及答案（Word版）一、填空题：〔共23分〕1.如图1,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后抵达△ACE的位置,那么旋转中心是；旋转角度是；点B的对应点是；点D的对应点是；线段CB的对应点是；∠B的对应角是；假设点M是CB的13,那么经过上述旋转后,点M移到了.2. 3点12分和3点40分时，时针与分针构成的角各是度和度.3.请你写出5个成中心对称的汉字,填在下面的横线上.4.如图2所示的四个图形中,图形(1)与图形成轴对称;图形(1)与图形成中心对称.(填写契合要求的图形所对应的符号)5.如图3所示,△ABC绕点A逆时针旋转某一角度失掉△ADE,假定∠1=∠2=∠3=20°,那么旋转角为度.6.如图4所示,线段AB=4cm,且CD⊥AB于O,那么阴影局部的面积是.7.如图5①,将字母〝V〞沿平移格会失掉字母〝W〞。

如图5②，将字母〝V〞绕点旋转度后失掉字母N,绕点旋转度后会失掉字母X.(图中E、F区分是其所在线段的中点)8.如图6是由面积为1的单位正三角形经过平移旋转,拼成由24个相反的三角形组成的正六边形,我们把面积为4的正三角形称为〝希望杯〞，那么图中可数出个不同的〝希望杯〞.9.在直角坐标系中，点A〔2，-3〕关于原点对称的坐标是.10. 在以下图7的四个图案中，既是轴对称图形，又是中心对称图形的有个.图7二、选择题：〔共40分〕11.观察以下图形,其中是旋转对称图形的有( )A.1个B.2个C.3个D.4个(1) (2) (3) (4)12.你玩过扑克牌吗?你细心观察过每张扑克牌中的图案吗?请你指出图案是中心对称图形的一组为( )A.黑桃6与黑桃9B.红桃6与红桃9C.梅花6与梅花9D.方块6与方块913.在平面直角坐标系中,点P(2,1)关于原点对称的点在( )A.第一象限B.第二象限C.第三象限D.第四象限14. 以下图形中，是．中心对称图形的为〔〕ＡＢＣ D15.以下图形中是中心对称图形的是A B C D16.在以下四个图案中，既是轴对称图形，又是中心对称图形的是( )A B C D17．以下图案都是由宁母〝m 〞经过变形、组合而成的．其中不是中心对称图形的是( )18．将下面的直角梯形绕直线 l 旋转一周，可以失掉左边平面图形的 ．〔 〕 19.数学课上，教员让同窗们观察如图 8 所示的图形，问：它绕着圆 心 O 旋转多少度后和它自身重合？甲同窗说：45°；乙同窗说：60°； 丙同窗说：90°；丁同窗说：135°。

精品基础教育教学资料，仅供参考，需要可下载使用！人教版九年级上册数学《第23章旋转》单元测试题一．选择题（共10小题）1．下列图形中，由原图旋转得到的是（）A．B．C．D．2．如图，Rt△ABC中，∠ACB＝90°，线段BC绕点B逆时针旋转α°（0＜α＜180）得到线段BD，过点A作AE⊥射线CD于点E，则∠CAE的度数是（）A．90﹣αB．αC．D．3．下列图形绕某点旋转90°后，不能与原来图形重合的是（）A．B．C．D．4．在平面直角坐标系中，把点P（﹣5，4）向右平移9个单位得到点P1，再将点P1绕原点顺时针旋转90°得到点P2，则点P2的坐标是（）A．（4，﹣4）B．（4，4）C．（﹣4，﹣4）D．（﹣4，4）5．下列四张扑克牌图案，属于中心对称的是（）A．B．C．D．6．下列“数字图形”中，既是轴对称图形，又是中心对称图形的有（）A．1个B．2个C．3个D．4个7．点P（2，﹣1）关于原点中心对称的点的坐标是（）A．（2，1）B．（﹣2，﹣1）C．（﹣1，2）D．（﹣2，1）8．如图，是用围棋子摆出的图案，围棋子的位置用有序数对表示，如：A点在（5，1），若再摆放一枚黑棋子，要使8枚棋子组成的图案是轴对称图形，则下列摆放错误的是（）A．黑（2，3）B．黑（3，2）C．黑（3，4）D．黑（3，1）9．在A、B、C、D四幅图案中，能通过图平移得到的是（）A．B．C．D．10．如图，在网格图中选择一个格子涂阴影，使得整个图形是以虚线为对称轴的轴对称图形，则把阴影凃在图中标有数字（）的格子内．A．1 B．2 C．3 D．4二．填空题（共8小题）11．如图，将△ABC绕着点A旋转，使点B恰好落在BC边上，得△AB'C，如果∠BAB'＝32°，且AC'∥BC，那么∠B'AC＝度．12．如图，△ABC为等边三角形，AB＝3，若点P为△ABC内一动点，且满足∠PAB＝∠ACP，则线段PB长度的最小值为．13．如图，等边△AOB绕点O逆时针旋转到△A′OB′的位置，∠A′OB＝80°，则△AOB旋转了度．14．已知点A（a，1）与点A（4，b）关于原点对称，则a+b＝．15．在棋盘中建立如图所示的平面直角坐标系，三颗棋子A，O，B的位置如图所示，它们的坐标分别是（﹣1，1），（0，0）和（1，0），在其他点位置添加一颗棋子P，使A，O，B，P四颗棋子成为一个中心对称图形，请写出棋子P的位置坐标（写出1个即可）．16．下列4种图案中，是中心对称图形的有个．17．若数字串“000”和数字串“101”既是轴对称图形，又是中心对称图形，那么数字串“110”是图形（填写“轴对称”、“中心对称”）．18．如图，在平面直角坐标系中，将△ABO绕点A顺指针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去……，若点A（，0），B（0，4），则点B2019的横坐标为．三．解答题（共7小题）19．如图，△AEC绕A点顺时针旋转60°得△APB，∠PAC＝20°，求∠BAE．20．如图所示，点D是等边△ABC内一点，DA＝13，DB＝19，DC＝21，将△ABD绕点A逆时针旋转到△ACE的位置，求△DEC的周长．21．如图所示的两个图形成中心对称，请找出它的对称中点．22．如图，方格纸的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC 的顶点均在格点上．（1）画出△ABC关于原点对称的△A1B1C1；（2）画出△ABC向上平移5个单位后的△A2B2C2，并求出平移过程中△ABC扫过的面积．23．如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．（1）旋转中心是点，旋转角度是度．（2）若连结EF，则△AEF是三角形；并证明．24．如图，Rt△ABC中，∠C＝90°，把Rt△ABC绕着B点逆时针旋转，得到Rt△DBE，点E在AB 上．（1）若∠BDA＝70°，求∠BAC的度数；（2）若BC＝8，AC＝6，求△ABD中AD边上的高．25．在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为θ（0°＜θ＜180°），得到△A'B'C．（1）如图1，当AB∥CB'时，设A'B'与CB相交于点D，求证：△A'CD是等边三角形．（2）若E为AC的中点，P为A'B'的中点，则EP的最大值是多少，这时旋转角θ为多少度．人教版九年级上册数学《第23章旋转》单元测试题参考答案与试题解析一．选择题（共10小题）1．下列图形中，由原图旋转得到的是（）A．B．C．D．【分析】旋转是围绕一点旋转一定的角度的图形变换，因而旋转一定有旋转中心和旋转角，且旋转前后图形能够重合，这是判断旋转的关键，据此解答即可．【解答】解：A、是由图形通过轴对称得到的；B、是由图形通过轴对称得到的；C、是通过轴对称和旋转得到的；D、是由图形通过顺时针旋转90°得到的．故选：D．【点评】此题主要考查了旋转的性质，旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．2．如图，Rt△ABC中，∠ACB＝90°，线段BC绕点B逆时针旋转α°（0＜α＜180）得到线段BD，过点A作AE⊥射线CD于点E，则∠CAE的度数是（）A．90﹣αB．αC．D．【分析】先利用旋转的性质得∠CBD＝α，BC＝BD，再根据等腰三角形的性质和三角形内角和定理得到∠BCD＝90°﹣α，然后利用互余表示出∠ACE，从而利用互余可得到∠CAE的度数．【解答】解：∵线段BC绕点B逆时针旋转α°（0＜α＜180）得到线段BD，∴∠CBD＝α，BC＝BD，∴∠BCD＝∠BDC，∴∠BCD＝（180°﹣α）＝90°﹣α，∵∠ACB＝90°，∴∠ACE＝90°﹣∠BCD＝90°﹣（90°﹣α）＝α，∵AE⊥CE，∴∠CAE＝90°﹣∠ACE＝90°﹣α．故选：C．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．3．下列图形绕某点旋转90°后，不能与原来图形重合的是（）A．B．C．D．【分析】根据旋转对称图形的概念作答．【解答】解：A、绕它的中心旋转90°能与原图形重合，故本选项不合题意；B、绕它的中心旋转90°能与原图形重合，故本选项不合题意；C、绕它的中心旋转90°能与原图形重合，故本选项不合题意；D、绕它的中心旋转120°才能与原图形重合，故本选项符合题意．故选：D．【点评】本题考查了旋转对称图形的知识，如果某一个图形围绕某一点旋转一定的角度（小于360°）后能与原图形重合，那么这个图形就叫做旋转对称图形．4．在平面直角坐标系中，把点P（﹣5，4）向右平移9个单位得到点P1，再将点P1绕原点顺时针旋转90°得到点P2，则点P2的坐标是（）A．（4，﹣4）B．（4，4）C．（﹣4，﹣4）D．（﹣4，4）【分析】首先利用平移的性质得出P1（4，4），再利用旋转变换的性质可得结论；【解答】解：∵P（﹣5，4），点P（﹣5，4）向右平移9个单位得到点P1∴P1（4，4），∴将点P1绕原点顺时针旋转90°得到点P2，则点P2的坐标是（4，﹣4），故选：A．【点评】本题考查坐标与图形变化﹣旋转以及平移，解题的关键是理解题意，熟练掌握基本知识，属于中考基础题．5．下列四张扑克牌图案，属于中心对称的是（）A．B．C．D．【分析】根据中心对称图形的概念和各扑克牌的花色排列特点的求解．【解答】解：A、是中心对称图形，符合题意；B、不是中心对称图形，不符合题意；C、不是中心对称图形，不符合题意；D、不是中心对称图形，不符合题意．故选：A．【点评】本题考查中心对称的知识，掌握好中心对称图形的概念是解题的关键．如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．6．下列“数字图形”中，既是轴对称图形，又是中心对称图形的有（）A．1个B．2个C．3个D．4个【分析】根据轴对称图形与中心对称图形的概念判断即可．【解答】解：第一个图形不是轴对称图形，是中心对称图形；第二、三个图形是轴对称图形，也是中心对称图形，第四个图形不是轴对称图形，不是中心对称图形；故选：B．【点评】本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．7．点P（2，﹣1）关于原点中心对称的点的坐标是（）A．（2，1）B．（﹣2，﹣1）C．（﹣1，2）D．（﹣2，1）【分析】平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y）．【解答】解：根据中心对称的性质，得点P（2，﹣1）关于中心对称的点的坐标为（﹣2，1）．故选：D．【点评】此题主要考查了关于原点对称的点坐标的关系，记忆方法是结合平面直角坐标系的图形记忆．8．如图，是用围棋子摆出的图案，围棋子的位置用有序数对表示，如：A点在（5，1），若再摆放一枚黑棋子，要使8枚棋子组成的图案是轴对称图形，则下列摆放错误的是（）A．黑（2，3）B．黑（3，2）C．黑（3，4）D．黑（3，1）【分析】根据轴对称图形定义：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．【解答】解：要使8枚棋子组成的图案是轴对称图形，则黑子可以摆放在横坐标为3的格点上，故摆放错误的是A，故选：A．【点评】此题主要考查了轴对称图形，关键是掌握轴对称图形定义．9．在A、B、C、D四幅图案中，能通过图平移得到的是（）A．B．C．D．【分析】根据平移后对应点的连线平行且相等可得答案．【解答】解：能通过图甲平移得到的是B，故选：B．【点评】此题主要考查了图形的平移，关键是掌握图形的平移只改变图形的位置，而不改变图形的形状、大小和方向．10．如图，在网格图中选择一个格子涂阴影，使得整个图形是以虚线为对称轴的轴对称图形，则把阴影凃在图中标有数字（）的格子内．A．1 B．2 C．3 D．4【分析】从阴影部分图形的各顶点向虚线作垂线并延长相同的距离找对应点，然后顺次连接各点可得答案．【解答】解：如图所示，把阴影凃在图中标有数字3的格子内所组成的图形是轴对称图形，故选：C．【点评】本题考查的是作简单平面图形轴对称后的图形，其依据是轴对称的性质，基本作法：①先确定图形的关键点；②利用轴对称性质作出关键点的对称点；③按原图形中的方式顺次连接对称点．二．填空题（共8小题）11．如图，将△ABC绕着点A旋转，使点B恰好落在BC边上，得△AB'C，如果∠BAB'＝32°，且AC'∥BC，那么∠B'AC＝42 度．【分析】先利用旋转的性质得到∠CAC′＝∠BAB'＝32°，AB＝AB′，再根据等腰三角形性质和三角形内角和定理计算出∠B＝74°，接着利用平行线的性质得到∠B′AC′＝∠AB′B＝74°，然后计算∠B′AC﹣∠CAC′即可．【解答】解：∵△ABC绕着点A旋转，使点B恰好落在BC边上，得△AB'C，∴∠CAC′＝∠BAB'＝32°，AB＝AB′，∵AB＝AB′∴∠B＝∠AB′B＝（180°﹣32°）＝74°，∵AC'∥BC，∴∠B′AC′＝∠AB′B＝74°，∴∠B'AC＝∠B′AC﹣∠CAC′＝74°﹣32°＝42°．故答案为42．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．12．如图，△ABC为等边三角形，AB＝3，若点P为△ABC内一动点，且满足∠PAB＝∠ACP，则线段PB长度的最小值为．【分析】由等边三角形的性质得出∠ABC＝∠BAC＝60°，AC＝AB＝3，求出∠APC＝120°，当PB ⊥AC时，PB长度最小，设垂足为D，此时PA＝PC，由等边三角形的性质得出AD＝CD＝AC ＝，∠PAC＝∠ACP＝30°，∠ABD＝∠ABC＝30°，求出PD＝AD•tan30°＝AD＝，BD ＝AD＝，即可得出答案．【解答】解：∵△ABC是等边三角形，∴∠ABC＝∠BAC＝60°，AC＝AB＝2，∵∠PAB＝∠ACP，∴∠PAC+∠ACP＝60°，∴∠APC＝120°，∴点P的运动轨迹是，当O、P、B共线时，PB长度最小，设OB交AC于D，如图所示：此时PA＝PC，OB⊥AC，则AD＝CD＝AC＝，∠PAC＝∠ACP＝30°，∠ABD＝∠ABC＝30°，∴PD＝AD•tan30°＝AD＝，BD＝AD＝，∴PB＝BD﹣PD＝﹣＝．故答案为：．【点评】本题考查了等边三角形的性质、等腰三角形的性质、三角形内角和定理、勾股定理、三角函数等知识；熟练掌握等边三角形的性质是解决问题的关键．13．如图，等边△AOB绕点O逆时针旋转到△A′OB′的位置，∠A′OB＝80°，则△AOB旋转了140 度．【分析】∠AOA′就是旋转角，根据等边三角形的性质得出∠AOB等于60°，再根据∠BOA′等于90°，从而求出∠AOA′的度数．【解答】解：旋转角∠AOA′＝∠AOB+∠BOA′＝60°+80°＝140°．∴△AOB旋转了140度．故答案为：140．【点评】本题主要考查了旋转的性质，正确理解旋转角是解题的关键；此题较简单，解题时要能根据等边三角形的性质求出角的度数．14．已知点A（a，1）与点A（4，b）关于原点对称，则a+b＝﹣5 ．【分析】根据“两点关于原点对称，则两点的横、纵坐标都是互为相反数”解答．【解答】解：∵点A（a，1）与点A′（4，b）关于原点对称，∴a、b的值分别为﹣4，﹣1．所以a+b＝﹣1﹣4＝﹣5，故答案为：﹣5【点评】本题考查了关于原点对称的点的坐标：两点关于原点对称，则两点的横、纵坐标都是互为相反数．15．在棋盘中建立如图所示的平面直角坐标系，三颗棋子A，O，B的位置如图所示，它们的坐标分别是（﹣1，1），（0，0）和（1，0），在其他点位置添加一颗棋子P，使A，O，B，P四颗棋子成为一个中心对称图形，请写出棋子P的位置坐标（0，1）（写出1个即可）．【分析】直接利用中心对称图形的性质得出答案．【解答】解：如图所示：点P（0，1）答案不唯一．故答案为：（0，1）．【点评】此题主要考查了中心对称图形的性质，正确把握定义是解题关键．16．下列4种图案中，是中心对称图形的有 2 个．【分析】根据中心对称图形的概念即可求解．【解答】解：第1个图形，是中心对称图形，符合题意；第2个图形，不是中心对称图形，不符合题意；第3个图形，是中心对称图形，符合题意；第4个图形，不是中心对称图形，不符合题意．故答案为：2．【点评】本题考查了中心对称图形，掌握好中心对称图形，中心对称图形是要寻找对称中心，旋转180度后两部分重合．17．若数字串“000”和数字串“101”既是轴对称图形，又是中心对称图形，那么数字串“110”是轴对称图形（填写“轴对称”、“中心对称”）．【分析】根据轴对称图形的概念与中心对称图形的概念即可作答．【解答】解：根据对称图形的概念，知110仅是轴对称图形，对称轴为正中水平直线．【点评】掌握好轴对称图形的概念．轴对称图形的关键是寻找对称轴，对称轴两边图形折叠后可重合．18．如图，在平面直角坐标系中，将△ABO绕点A顺指针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去……，若点A（，0），B（0，4），则点B2019的横坐标为10096 ．【分析】由图象可知点B2019在第一象限，求出B2，B4，B6的坐标，探究规律后即可解决问题．【解答】解：由图象可知点B2019在x轴上，∵OA＝，OB＝4，∠AOB＝90°，∴AB＝，∴B2（10，4），B4（20，4），B6（30，4），…∴B2018（10090，4）．∴点B2019横坐标为10090++＝10096．故答案为：10096．【点评】本题考查坐标与图形的变化﹣旋转、勾股定理等知识，解题的关键是从特殊到一般探究规律，发现规律，利用规律解决问题，属于中考常考题型．三．解答题（共7小题）19．如图，△AEC绕A点顺时针旋转60°得△APB，∠PAC＝20°，求∠BAE．【分析】充分运用旋转的性质，旋转前后三角形全等，即△ABP≌△ACE，根据对应角相等，三角形内角和定理，对应边的夹角为旋转角，通过计算解答题目问题．【解答】解：根据旋转的性质可得△ABP≌△ACE，AC与AB是对应边，∠BAC＝∠BAP+∠PAC＝60°，∵∠PAC＝20°，∴∠CAE＝∠BAP＝40°，∴∠BAE＝∠BAC+∠CAE＝100°．【点评】本题考查旋转的性质，旋转变化前后，对应角分别相等，结合三角形内角和定理求出相关的角．20．如图所示，点D是等边△ABC内一点，DA＝13，DB＝19，DC＝21，将△ABD绕点A逆时针旋转到△ACE的位置，求△DEC的周长．【分析】先根据等边三角形的性质得∠BAC＝60°，AB＝AC，再根据旋转的性质得到AD＝AE，CE ＝BD＝19，∠DAE＝∠BAC＝60°，则可判断△ADE为等边三角形，从而得到DE＝AD＝13，然后计算△DEC的周长．【解答】解：∵△ABC为等边三角形，∴∠BAC＝60°，AB＝AC，∵△ABD绕点A逆时针旋转到△ACE的位置，∴AD＝AE，CE＝BD＝19，∠DAE＝∠BAC＝60°，∴△ADE为等边三角形，∴DE＝AD＝13，∴△DEC的周长＝DE+DC+CE＝13+21+19＝53．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等边三角形的性质．21．如图所示的两个图形成中心对称，请找出它的对称中点．【分析】根据关于中心对称的两个图形，对应点的连线都经过对称中心作图．【解答】解：连接CC′，BB′，两条线段相交于当O，则点O即为对称中点．【点评】本题考查的是中心对称的性质，掌握关于中心对称的两个图形，对应点的连线都经过对称中心，并且被对称中心平分是解题的关键．22．如图，方格纸的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC 的顶点均在格点上．（1）画出△ABC关于原点对称的△A1B1C1；（2）画出△ABC向上平移5个单位后的△A2B2C2，并求出平移过程中△ABC扫过的面积．【分析】（1）根据关于原点对称的点的坐标特征写出A1、B1、C1的坐标，然后描点即可；（2）利用网格特点和平移的性质画出A、B、C的对应点A2、B2、C2，然后计算一个矩形的面积加上△ABC的面积得到△ABC扫过的面积．【解答】解：（1）如图，△A1B1C1为所作；（2）如图，△A2B2C2为所作，△ABC扫过的面积＝5×4+×2×4＝24．【点评】本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．23．如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．（1）旋转中心是点A，旋转角度是90 度．（2）若连结EF，则△AEF是等腰直角三角形；并证明．【分析】（1）根据旋转变换的定义，即可解决问题；（2））根据旋转变换的定义，即可解决问题．【解答】解：（1）如图，由题意得：旋转中心是点A，旋转角度是90度．故答案为A、90．（2）等腰直角三角形由旋转得：AF＝AE，∠FAB＝∠EAD∴∠FAB+∠BAE＝∠EAD+∠BAE即∠FAE＝∠BAD∵四边形ABCD是正方形∴∠FAE＝∠BAD＝90°∴△AEF是等腰直角三角形故答案为等腰直角．【点评】本题主要考查了旋转变换的性质、正方形的性质及其应用问题；解题的关键是牢固掌握旋转变换的性质、正方形的性质，这是灵活运用、解题的基础和关键．24．如图，Rt△ABC中，∠C＝90°，把Rt△ABC绕着B点逆时针旋转，得到Rt△DBE，点E在AB 上．（1）若∠BDA＝70°，求∠BAC的度数；（2）若BC＝8，AC＝6，求△ABD中AD边上的高．【分析】（1）由旋转性质知BD＝BA、∠CBA＝∠EBD，据此可得∠BDA＝∠BAD＝70°，从而得∠ABD＝∠ABC＝40°，结合∠C＝90°可得答案；（2）由旋转性质得BE＝BC＝8、DE＝AC＝6、AB＝BD＝10，从而得AE＝2，利用勾股定理知AD ＝2，作BF⊥AD得AF＝AD＝，再次利用勾股定理可得答案．【解答】解：（1）由旋转性质知BD＝BA、∠CBA＝∠EBD，∵∠BDA＝70°，∴∠BAD＝70°，∴∠ABD＝∠ABC＝40°，∵∠C＝90°，∴∠BAC＝50°；（2）∵BC＝8、AC＝6，∠C＝90°，∴AB＝10，由旋转性质知△ABC≌△DBE，则BE＝BC＝8、DE＝AC＝6，∴AE＝2，在Rt△ADE中，AD＝＝＝2，作BF⊥AD于点F，∵BA＝BD，∴AF＝AD＝，则BF＝＝＝3．【点评】本题主要考查旋转的性质，解题的关键是掌握旋转的性质：①对应点到旋转中心的距离相等．②对应点与旋转中心所连线段的夹角等于旋转角．③旋转前、后的图形全等．也考查了等腰三角形的性质和勾股定理．25．在△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕顶点C顺时针旋转，旋转角为θ（0°＜θ＜180°），得到△A'B'C．（1）如图1，当AB∥CB'时，设A'B'与CB相交于点D，求证：△A'CD是等边三角形．（2）若E为AC的中点，P为A'B'的中点，则EP的最大值是多少，这时旋转角θ为多少度．【分析】（1）当AB∥CB′时，∠BCB′＝∠B＝∠B′＝30°，则∠A′CD＝90°﹣∠BCB′＝60°，∠A′DC＝∠BCB′+∠B′＝60°，可证：△A′CD是等边三角形；（2）连接CP，当E、C、P三点共线时，EP最长，根据图形求出此时的旋转角及EP的长．【解答】（1）证明：∵AB∥CB′，∴∠B＝∠BC B′＝30°，∴∠BC A′＝90°﹣30°＝60°，∵∠A′＝∠A＝60°，∴△A′CD是等边三角形；（2）解：如图，连接CP，当△ABC旋转到E、C、P三点共线时，EP最长，此时θ＝∠ACA1＝120°，∵∠B′＝30°，∠A′CB′＝90°，设AC＝a，∴A′C＝AC＝A′B′＝a，∵AC中点为E，A′B′中点为P，∠A′CB′＝90°∴CP＝A′B′＝a，EC＝a，∴EP＝EC+CP＝a+a＝AC．【点评】此题考查了旋转的性质，特殊三角形的判定与性质，相似三角形的判断与性质．关键是根据旋转及特殊三角形的性质证明问题．。

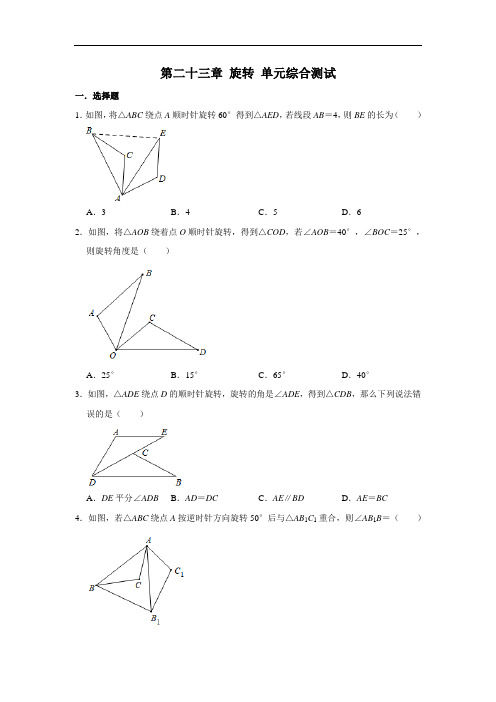
第二十三章旋转单元综合测试一．选择题1．如图，将△ABC绕点A顺时针旋转60°得到△AED，若线段AB＝4，则BE的长为（）A．3B．4C．5D．62．如图，将△AOB绕着点O顺时针旋转，得到△COD，若∠AOB＝40°，∠BOC＝25°，则旋转角度是（）A．25°B．15°C．65°D．40°3．如图，△ADE绕点D的顺时针旋转，旋转的角是∠ADE，得到△CDB，那么下列说法错误的是（）A．DE平分∠ADB B．AD＝DC C．AE∥BD D．AE＝BC4．如图，若△ABC绕点A按逆时针方向旋转50°后与△AB1C1重合，则∠AB1B＝（）A．50°B．55°C．60°D．65°5．下列图案中，既是中心对称图形又是轴对称图形的是（）A．B．C．D．6．如图，将△ABC绕点C（0，）旋转180°得到△A'B'C，设点A的坐标为（a，b），则点A'的坐标为（）A．（﹣a，﹣b）B．（a，﹣b+2）C．（﹣a，﹣b+）D．（﹣a，﹣b+2）7．如图，将等边△AOB放在平面直角坐标系中，点A的坐标为（0，4），点B在第一象限，将等边△AOB绕点O顺时针旋转180°得到△A′OB′，则点B的对应点B′的坐标是（）A．B．C．D．（0，﹣4）8．如图，在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°得到△BAE，连接ED，若BC＝8，BD＝7，则△AED的周长是（）A．15B．14C．13D．129．如图，CD是△ABC的边AB上的中线，将线段AD绕点D顺时针旋转90°后，点A的对应点E恰好落在AC边上，若AD＝，BC＝，则AC的长为（）A．B．3C．2D．410．在平面直角坐标系xOy中，点A（4，3），点B为x轴正半轴上一点，将△AOB绕其一顶点旋转180°，连接其余四个顶点得到一个四边形，若该四边形是一个轴对称图形，则满足条件的点有（）A．5个B．4个C．3个D．2个二．填空题11．如图，四角星的顶点是一个正方形的四个顶点，将这个四角星绕其中心旋转，当第一次与自身重合时，其旋转角的大小是度．12．一副三角尺按如图的位置摆放（顶点C与F重合，边CA与边FE叠合，顶点B、C、D 在一条直线上）．将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180），如果EF⊥AB，那么n的值是．13．如图，在Rt△ABC，∠B＝90°，∠ACB＝50°．将Rt△ABC在平面内绕点A逆时针旋转到△AB'C'的位置，连接CC'．若AB∥CC'，则旋转角的度数为°．14．如图，在正方形ABCD中，AB＝4，点M在CD边上，且DM＝1，△AEM与△ADM关于AM所在直线对称，将△ADM按顺时针方向绕点A旋转90°得到△ABF，连接EF，则线段EF的长为．15．已知点A（x﹣2，3）与B（x+4，y﹣5）关于原点对称，则xy的值是．16．如图，△ABC和△DEC关于点C成中心对称，若AC＝1，AB＝2，∠BAC＝90°，则AE的长是．17．已知点P（a﹣3，2﹣a）关于原点对称的点在第四象限，则a的取值范围是．18．用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为a，小正方形地砖面积为b，依次连接四块大正方形地砖的中心得到正方形ABCD．则正方形ABCD的面积为．（用含a，b的代数式表示）19．在平面直角坐标系中，△OAB的位置如图所示，将△OAB绕点O顺时针旋转90°得△OA1B1；再将△OA1B1绕点O顺时针旋转90°得△OA2B2；再将△OA2B2绕点O顺时针旋转90°得△OA3B3；……依此类推，第2020次旋转得到△OA2020B2020，则项点A的对应点A2020的坐标是．三．解答题20．在平面直角坐标系中，已知点P（a，﹣1），请解答下列问题：（1）若点P在第三象限，则a的取值范围为；（2）若点P在y轴上，则a的值为；（3）当a＝2时，点P关于y轴对称的点的坐标为点P关于原点对称的点的坐标为．21．如图，在△ABC中，AB＝BC，∠ABC＝120°，点D在边AC上，且线段BD绕着点B 按逆时针方向旋转120°能与BE重合，点F是ED与AB的交点．（1）求证：AE＝CD；（2）若∠DBC＝45°，求∠BFE的度数．22．如图所示，把△ABC绕点A旋转至△ADE位置，延长BC交AD于F，交DE于G，若∠CAD＝10°，∠D＝25°，∠EAB＝120°，求∠DFB的度数．23．已知点A（﹣1，3a﹣1）与点B（2b+1，﹣2）关于x轴对称，点C（a+2，b）与点D 关于原点对称．（1）求点A、B、C、D的坐标；（2）顺次联结点A、D、B、C，求所得图形的面积．24．如图，正△ABC与正△A1B1C1关于某点中心对称，已知A，A1，B三点的坐标分别是（0，4），（0，3），（0，2）．（1）求对称中心的坐标；（2）写出顶点C，C1的坐标．25．如图，在△ABC中，AB＝AC，△ABC与△DEC关于点C成中心对称，连接AE、BD．（1）线段AE、BD具有怎样的位置关系和大小关系？说明你的理由．（2）如果△ABC的面积为5cm2，求四边形ABDE的面积．（3）当∠ACB为多少度时，四边形ABDE为矩形？说明你的理由．参考答案1．解：∵△ABC绕点A顺时针旋转60°得到△AED，∴AB＝AE，∠BAE＝60°，∴△AEB是等边三角形，∴BE＝AB，∵AB＝4，∴BE＝4．故选：B．2．解：∵∠AOB＝40°，∠BOC＝25°，∴∠AOC＝65°，∵将△AOB绕着点O顺时针旋转，得到△COD，∴旋转角为∠AOC＝65°，故选：C．3．解：将△ADE绕点D顺时针旋转，得到△CDB，∴∠ADE＝∠CDB，AD＝CD，AE＝BC，故A、B、D选项正确；∵∠B＝∠E，但∠B不一定等于∠BDC，∴BD不一定平行于AE，故C选项错误；故选：C．4．解：∵△ABC绕点A按逆时针方向旋转50°后与△AB1C1重合，∴AB＝AB1，∠BAB1＝50°，∴∠AB1B＝（180°﹣50°）＝65°．故选：D．5．解：A、是轴对称图形，不是中心对称图形，不符合题意；B、既不是轴对称图形，也不是中心对称图形，不符合题意；C、不是轴对称图形，是中心对称图形，不符合题意；D、既是轴对称图形，又是中心对称图形，符合题意．故选：D．6．解：将点A的坐标为（a，b）向下平移个单位，得到对应点坐标为（a，b），再将其绕原点旋转180°可得对称点坐标为（﹣a，﹣b+），然后再向上平移个单位可得点A'的坐标为（﹣a，﹣b+2），故选：D．7．解：作BH⊥y轴于H，如图，∵△OAB为等边三角形，∴OH＝AH＝2，∠BOA＝60°，∴BH＝OH＝2，∴B点坐标为（2，2），∵等边△AOB绕点O顺时针旋转180°得到△A′OB′，∴点B′的坐标是（﹣2，﹣2）．故选：C．8．解：∵将△BCD绕点B逆时针旋转60°得到△BAE，∴BD＝BE，∠DBE＝60°，CD＝AE，∴△DBE是等边三角形，∴BD＝DE＝7，∴△AED的周长＝AE+AD+DE＝CD+AD+DE＝8+7＝15，故选：A．9．解：如图，连接BE，∵CD是△ABC的边AB上的中线，∴AD＝BD，∵将线段AD绕点D顺时针旋转90°，∴AD＝DE，∠ADE＝90°，∴∠A＝45°，AE＝AD＝2，AD＝DE＝BD，∴∠AEB＝90°，∴∠A＝∠ABE＝45°，∴AE＝BE＝2，∴EC＝＝＝1，∴AC＝AE+EC＝3，故选：B．10．解：观察图象可知，满足条件的点B有5个．故选：A．11．解：该图形被平分成四部分，旋转90°的整数倍，就可以与自身重合，故当此图案第一次与自身重合时，其旋转角的大小为90°．故答案为：90．12．解：如图1，延长EF交AB于H，∵EF⊥AB，∠A＝45°，∴∠ACH＝45°，∴∠ACE＝135°，∴n＝135；如图2，∵EF⊥AB，∠A＝45°，∴∠ACE＝45°，∴n＝360﹣45＝315，∵0＜n＜180，∴n＝315不合题意舍去，故答案为：135．13．解：∵AB∥CC'，∴∠ABC+∠C′CB＝180°，而∠B＝90°，∴∠C′CB＝90°，∴∠ACC′＝90°﹣∠ACB＝90°﹣50°＝40°，∵Rt△ABC在平面内绕点A逆时针旋转到△AB'C'的位置，∴AC＝AC′，∠C′AC等于旋转角，∴∠AC′C＝∠ACC′＝40°，∴∠C′AC＝180°﹣40°﹣40°＝100°，即旋转角为100°．故答案为100．14．解：如图，连接BM．∵△AEM与△ADM关于AM所在的直线对称，∴AE＝AD，∠MAD＝∠MAE．∵△ADM按照顺时针方向绕点A旋转90°得到△ABF，∴AF＝AM，∠F AB＝∠MAD．∴∠F AB＝∠MAE，∴∠F AB+∠BAE＝∠BAE+∠MAE．∴∠F AE＝∠MAB．∴△F AE≌△MAB（SAS）．∴EF＝BM．∵四边形ABCD是正方形，∴BC＝CD＝AB＝4．∵DM＝1，∴CM＝3．∴在Rt△BCM中，BM＝＝5，∴EF＝5，故答案为：5．15．解：∵点A（x﹣2，3）与B（x+4，y﹣5）关于原点对称，∴x﹣2+x+4＝0，3+y﹣5＝0，解得：x＝﹣1，y＝2，则xy的值是：﹣2．故答案为：﹣2．16．解：∵△DEC与△ABC关于点C成中心对称，∴△ABC≌△DEC，∴AB＝DE＝2，AC＝DC＝1，∠D＝∠BAC＝90°，∴AD＝2，∵∠D＝90°，∴AE＝＝2，故答案为2．17．解：∵点P（a﹣3，2﹣a）关于原点对称的点在第四象限，∴点P（a﹣3，2﹣a）在第二象限，，解得：a＜2．∴故答案为：a＜2．18．解：如图，连接DK，DN，∵∠KDN＝∠MDT＝90°，∴∠KDM＝∠NDT，∵DK＝DN，∠DKM＝∠DNT＝45°，∴△DKM≌△DNT（ASA），∴S△DKM＝S△DNT，∴S四边形DMNT＝S△DKN＝a，∴正方形ABCD的面积＝4×a+b＝a+b．故答案为（a+b）．19．解：将△OAB绕点O顺时针旋转90°得△OA1B1；此时，点A1的坐标为（2，﹣1）；再将△OA1B1绕点O顺时针旋转90°得△OA2B2；此时，点A2的坐标为（﹣1，2）；再将△OA2B2绕点O顺时针旋转90°得△OA3B3；此时，点A3的坐标为（﹣2，1）；再将△OA3B3绕点O顺时针旋转90°得△OA4B4；此时，点A4的坐标为（1，2）；∴每旋转4次一个循环，∵2020÷4＝505，∴第2020次旋转得到△OA2020B2020，则顶点A的对应点A2020的坐标与点A4的坐标相同，为（1，2）；故答案为：（1，2）．20．解：（1）∵点P（a，﹣1），点P在第三象限，∴a＜0；故答案为：a＜0；（2）∵点P（a，﹣1），点P在y轴上，∴a＝0；故答案为：0；（3）当a＝2时，点P（a，﹣1）的坐标为：（2，﹣1）关于y轴对称的点的坐标为：（﹣2，﹣1），点P关于原点对称的点的坐标为：（﹣2，1）．故答案为：（﹣2，﹣1），（﹣2，1）．21．（1）证明：∵线段BD绕着点B按逆时针方向旋转120°能与BE重合，∴BD＝BE，∠EBD＝120°，∵AB＝BC，∠ABC＝120°，∴∠ABD+∠DBC＝∠ABD+∠ABE＝120°，∴∠DBC＝∠ABE，∴△ABE≌△CBD（SAS），∴AE＝CD；（2）解：由（1）知∠DBC＝∠ABE＝45°，BD＝BE，∠EBD＝120°，∴∠BED＝∠BDE＝（180°﹣120°）＝30°，∴∠BFE＝180°﹣∠BED﹣∠ABE＝180°﹣30°﹣45°＝105°．22．解：由旋转可知：△ABC≌△ADE，∵∠D＝25°，∴∠B＝∠D＝25°，∠EAD＝∠CAB，∵∠EAB＝∠EAD+∠CAD+∠CAB＝120°，∠CAD＝10°，∴∠CAB＝（120°﹣10°）÷2＝55°，∴∠F AB＝∠CAB+∠CAD＝55°+10°＝65°，∵∠DFB是△ABF的外角，∴∠DFB＝∠B+∠F AB，∴∠DFB＝25°+65°＝90°．23．解：（1）∵点A（﹣1，3a﹣1）与点B（2b+1，﹣2）关于x轴对称，∴2b+1＝﹣1，3a﹣1＝2，解得a＝1，b＝﹣1，∴点A（﹣1，2），B（﹣1，﹣2），C（3，﹣1），∵点C（a+2，b）与点D关于原点对称，∴点D（﹣3，1）；（2）如图所示：四边形ADBC的面积为：．24．解：（1）∵A，A1，B三点的坐标分别是（0，4），（0，3），（0，2），所以对称中心的坐标为（0，2.5）；（2）等边三角形的边长为4﹣2＝2，所以点C的坐标为（，3），点C1的坐标（，2）．25．解：（1）∵△ABC与△DEC关于点C成中心对称，∴AC＝CD，BC＝CE，∴四边形ABDE是平行四边形，∴AE与BD平行且相等；（2）∵四边形ABDE是平行四边形，∴S△ABC＝S△BCD＝S△CDE＝S△ACE，∵△ABC的面积为5cm2，∴四边形ABDE的面积＝4×5＝20cm2；（3）∠ACB＝60°时，四边形ABDE为矩形．理由如下：∵AB＝AC，∠ACB＝60°，∴△ABC是等边三角形，∴AC＝BC，∵四边形ABDE是平行四边形，∴AD＝2AC，BE＝2BC，∴AD＝BE，∴四边形ABDE为矩形．。

第23章 旋转单元测试（附解析）学校:___________姓名：___________班级：___________考号：___________总分120分，考试时间120分钟一、单选题(共10个小题，每小题3分，共30分)1．下列与杭州亚运会有关的图案中，中心对称图形是（ ）A ．B ．C ．D ． 2．2022年冬奥会将在我国北京市和张家口市联合举行，下列历届冬奥会会徽的部分图案中，是中心对称图形的是（ ）A ．B ．C ．D ． 3．平面直角坐标系内一点P （－2，3）关于原点对称的点的坐标是（ ）A ．（3，2）B ．（－2，－3）C ．（2，－3）D ．（2，3）4．如图，矩形ABCD 的顶点1,0A ，()0,2D ，()5,2B ，将矩形以原点为旋转中心，顺时针旋转75°之后点C 的坐标为（ ）A ．()4,2-B ．()42,22-C ．()42,2-D ．()26,22- 5．如图，在钝角△ABC 中，35BAC ∠=︒，将ABC 绕点A 顺时针旋转70︒得到ADE ，点B ，C 的对应点分别为D ，E ，连接BE ．则下列结论一定正确的是（ ）A ．ABC AED ∠=∠B ．AC DE = C ．AD BE AC += D ．AE 平分BED ∠ 6．平面直角坐标系中，O 为坐标原点，点A 的坐标为()5,1-，将OA 绕原点按逆时针方向旋转90︒得OB ，则点B 的坐标为（ ）A ．()5,1-B ．()1,5--C ．()5,1--D ．()1,5-7．如图，在Rt ABC 中，90BAC ∠=︒，AB AC =，点D 为BC 的中点，直角MDN ∠绕点D 旋转，DM ，DN 分别与边AB ，AC 交于E ，F 两点，下列结论：①DEF 是等腰直角三角形；②AE CF =；③12ABC AEDF S S =△四边形；④BE CF EF +=，其中正确结论的个数是（ ）A ．1B ．2C ．3D ．48．在矩形ABCD 中，AB ＝4，BC ＝3，CE ＝2BE ，EF ＝2，连按AF ，将线段AF 绕着点A 顺时针旋转90°得到AP ，则线段PE 的最小值为( )A ．25B ．342-C ．4D ．341+9．如图，在Rt △ABC 中，∠ACB ＝90°，2AC BC ==将△ABC 绕点A 逆时针旋转60°，得到△ADE ，连接BE ，则12BE AB +的值为（ ）A 6B ．22C 3D 210．如图，P 是正三角形ABC 内的一点，且6PA =，8PB =，10PC =．若将PAC △绕点A 逆时针旋转后，得到MAB △，则APB ∠等于（ ）．A ．120°B ．135°C ．150°D ．160°二、填空题(共10个小题，每小题3分，共30分)11．如图所示，P 是正方形ABCD 内一点，将△ABP 绕点B 按顺时针方向旋转能与△CBP '重合，若PB ＝3，则PP '＝__________12．若点P （a －1，5）与点Q （5，1－b ）关于原点成中心对称，则a ＋b ＝_________． 13．对于下列图形：①等边三角形； ②矩形； ③平行四边形； ④菱形； ⑤正八边形；⑥圆．其中既是轴对称图形，又是中心对称图形的是_________________．（填写图形的相应编号） 14．若点P （a ，2）点Q （﹣4，b ）关于原点对称，则点M （a ，b ）在第___象限．15．如图，△ABC 为等边三角形，D 是△ABC 内一点，若将△ABD 经过旋转后到△ACP 位置，则旋转角等于___________度．16．如图，在矩形ABCD 中，23AB =6BC =，点E 是直线BC 上的一个动点，连接DE ，将线段DE 绕着点D 顺时针旋转120︒得到线段DG ，连接AG ，则线段AG 的最小值为_________．17．如图，△ABC 边长为1的正三角形，BDC 是顶角120BDC ∠=︒的等腰三角形，以D 为顶点作一个60度角，角的两边分别交AB 于M ，交AC 于N ，连结MN ，则AMN 的周长为__________．18．如图，在Rt △ABC 中，90ACB ∠=，30BAC ∠=，BC ＝2，线段BC 绕点B 旋转到BD ，连AD ，E 为AD 的中点，连接CE ，则CE 的最大值是___．19．如图，在△ABC 中，3AB =，2AC =，60BAC ∠=︒，P 为ABC 内一点，则PA PB PC ++的最小值为__________．20．如图，点P 是等边三角形ABC 内一点，且6PA 2PB =22=PC ABC 的边长为________．三、解答题(共6个小题，每小题10分，共60分)21．如图，在△ABC 中，∠ACB ＝90°，∠B ＝60°，以C 为旋转中心，旋转一定角度后成△A ′B ′C ，此时B ′落在斜边AB 上，试确定∠ACA ′，∠BB ′C 的度数．22．四边形ABCD 各顶点坐标分别为(5,0)A ，(2,3)B -，(1,0)C -，(1,5)D --，作出与四边形ABCD 关于原点对称的图形．23．如图，在同一平面内，△BEC绕点B逆时针旋转60°得到△BAD，且AB⊥BC，BE＝CE．连接DE．（1）求证：△BDE≌△BCE；（2）试判断四边形ABED的形状，并说明理由．24．正方形ABCD中，点F为正方形ABCD内的点，BFC△绕着点B按逆时针方向旋转90︒后与△重合．BEA(1)如图①，若正方形ABCD的边长为2，1BE=，3FC=AE∥BF．(2)如图②，若点F为正方形ABCD对角线AC上的点(点F不与点A、C重合)，试探究AE、AF、BF之间的数量关系并加以证明．。

第一学期人教版九年级上册数学第23章《旋转》单元测试卷（含答案）一、填空题〔共10 小题，每题 3 分，共30 分〕1.如图，矩形OABC和ABEF，B(3, 4)．如图，矩形OABC和ABEF，B(3, 4)．(1)画出矩形OABC绕点O逆时针旋转90∘后的矩形OA1B1C1，并写出B1的坐标为________，点B运动到点B1所经过的途径的长为________；(2)假定点E的坐标为(5, 2)，那么点F的坐标为________，请画一条直线l平分矩形OABC与ABEF组成图形的面积〔保管必要的画图痕迹〕．2.如下图是日本三菱汽车的标志，它可以看作由一个菱形经过________次旋转，每次至少旋转________失掉的．3.如下图的图形为中心对称图形，点O为它的对称中心，写出一组关于点O的对称点是________．4.点A(−1, 2)关于y轴的对称点坐标是________；点A关于原点的对称点的坐标是________．5.点P坐标为(1, 1)，将点P绕原点逆时针旋转45∘得点P1，那么点P1的坐标为________．6.如图是4×4的正方形网格，再把其中一个白色小正方形涂上阴影，使整个阴影局部红为轴对称图形，这样的白色小正方形有________个．7.如下图，把甲图案〝扶直〞属于________变换．甲图案与乙图案外形、大小完全相反，假定让甲图案与乙图案重合，还需________变换．8.图中，甲图怎样变成乙图：________．9.如图，将△ABC绕点C按顺时针方向旋转64∘至△A′B′C，使点A′落在BC的延伸线上．那么∠ACB′=________度．10.如图，在直角坐标系中，点A(−3, 0)、B(0, 4)，对△OAB延续作旋转变换，依次失掉△1、△2、△3、△4，那么△2017的直角顶点的坐标为________．二、选择题〔共10 小题，每题 3 分，共30 分〕11.将点A(−2, 3)绕原点O旋转180∘失掉点P，那么点P的坐标是〔〕A.(2, 3)B.(−2, −3)C.(2, −3)D.(3, −2)12.如图，将两块大小相反的三角板堆叠在一同，∠A=30∘，∠B=60∘，BC=10cm，把下面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置，点B′在AB上，A′B′与AC相交于点D，那么A′D的长度为〔〕A.14cmB.15cmC.16cmD.17cm13.如图，四边形ABD与四边形FGHE关于一个点成中心对称，那么这个点是〔〕A.O1B.O2C.O3D.O414.要使正十二边形旋转后与自身重合，至少应将它绕中心旋转的度数为〔〕A.75∘B.60∘C.45∘D.30∘15.在以下由纸折叠而成的图案中，是中心对称图形的是〔〕A.B.C. D.16.将等腰直角三角形AOB按图放置，然后绕O点逆时针旋转90∘至A′OB′位置，点B(2, 0)，那么A的坐标〔〕A.(1, 1)B.(√2, √2)C.(−1, 1)D.(−√2, √2)17.在直角坐标系中，点A(−2, 3)与点B关于原点成中心对称，那么点B的坐标为〔〕A.(2, 3)B.(2, −3)C.(−2, −3)D.(−2, 3)18.平移、旋转与轴对称都是图形之间的一些主要变换，以下关于图形经这些变换后说法错误的〔〕A.对应线段的长度不变B.对应角的大小不变C.图形的外形和大小不变D.图形的位置不变19.如图，正三角形网格中，已有两个小正三角形被涂黑，随机将图中其他小正三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形的概率是〔〕A.1 7B.2 7C.37D.以上答案都不对20.如图，Rt△ABC中，∠C=90∘，AC=8，BC=6，△ABC绕着点B逆时针旋转90∘到△A′B′C′的位置，AA′的长为〔〕A.10√2B.10C.20D.5√2三、解答题〔共6 小题，每题10 分，共60 分〕21.(1)如图1，在正方形网格中，每个小正方形的边长均为1个单位．将△ABC向绕点C逆时针旋转90∘，失掉△A′B′C′，请你画出△A′B′C′〔不要求写画法〕．21.(2)如图2，点O和△ABC，试画出与△ABC关于点O成中心对称的图形．22.△ABC各顶点坐标区分为A(5, 1)，B(2, 3)，C(0, 0)，将它绕原点顺时针方向旋转90∘，失掉△A1B1C1(1)求A1，B1，C1的坐标；(2)求△A1B1C1的面积．23.将Rt△ABC绕顶点C区分旋转90∘、180∘、270∘失掉图所示的图形，衔接BB1、B1B2、B2B3、B3B，直角边BC=1，求四边形BB1B2B3的外形及其面积．24.某校九年级学习小组在探求学习进程中，用两块完全相反的且含60∘角的直角三角板ABC 与AFE按如下图(1)位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α(0∘<α< 90∘)，如图(2)，AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．(1)求证：AM=AN；(2)当旋转角α=30∘时，四边形ABPF是什么样的特殊四边形？并说明理由．25.(1)如图1，在△ABC中，绕点C旋转180∘后，失掉△CA′B′．请先画出变换后的图形，写出以下结论正确的序号是________．①△ABC≅△A′B′C；②线段AB绕C点旋转180∘后，失掉线段A′B′；③A′B′ // AB；④C是线段BB′的中点．在(1)的启示下解答下面效果：25.(2)如图2，在△ABC中，∠BAC=120∘，D是BC的中点，射线DF交BA于E，交CA的延伸线于F，请猜想∠F等于多少度时，BE=CF？〔直接写出结果，不证明〕(3)如图3，在△ABC中，假设∠BAC≠120∘，而(2)中的其他条件不变，假定BE=CF的结论依然成立，那么∠BAC与∠F满足什么数量关系〔等式表示〕并加以证明．26.阅读下面资料：如图(1)，把△ABC沿直线BC平行移动线段BC的长度，可以变到△DEC的位置；如图(2)，以BC为轴，把△ABC翻折180∘，可以变到△DBC的位置；如图(3)，以点A为中心，把△ABC旋转180∘，可以变到△AED的位置．像这样，其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的．这种只改动位置，不改动外形大小的图形变换，叫做三角形的全等变换．回答以下效果：①在图(4)中，可以经过平行移动、翻折、旋转中的哪一种方法怎样变化，使△ABE变到△ADF 的位置；②指图中线段BE与DF之间的关系，为什么？答案π(5, −2)1.(−4, 3)522.2120∘3.点A与点C4.(1, 2)(1, −2)5.(0, √2)6.47.旋转平移8.绕点A顺时针旋转9.5210.(8064, 0)11-20：CBADD CBDCA21.解：(1)(2)如下图：22.解：(1)如图，△ABC绕原点顺时针方向旋转90∘失掉△A1B1C1，点A1，B1，C1的坐标区分为(5, −1)，(3, −2)，(0, 0)；(2)△A1B1C1的面积=5×2−12×2×3−12×2×1−12×1×5=3.5．23.解：∵将Rt△ABC绕顶点C区分旋转90∘、180∘、270∘失掉图所示的图形，直角边BC=1，∵BC=CB1=CB2=CB3=1，∠B1CB2=∠B1CB=∠B2CB3=∠BCB3=90∘，∵BB1=BB3=B2B3=B1B3，B1B3=BB2，∵四边形BB1B2B3为正方形，∵BB1B2B3的面积为：2×2×12=2．24.(1)证明：∵用两块完全相反的且含60∘角的直角三角板ABC与AFE按如下图(1)位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α(0∘<α<90∘)，∵AB=AF，∠BAM=∠FAN，在△ABM和△AFN中，{∠FAN=∠BAM AB=AF∠B=∠F，∵△ABM≅△AFN(ASA)，∵AM=AN；(2)解：当旋转角α=30∘时，四边形ABPF是菱形．理由：衔接AP，∵∠α=30∘，∵∠FAN=30∘，∵∠FAB=120∘，∵∠B=60∘，∵∠B+∠FAB=180∘，∵AF // BP，∵∠F=∠FPC=60∘，∵∠FPC=∠B=60∘，∵AB // FP，∵四边形ABPF是平行四边形，∵AB=AF，∵平行四边形ABPF是菱形．25.解：(1)依据旋转的性质，知①②③④都是正确的．(2)60∘．(3)等量关系：∠BAC=2∠F．作△FCD关于点D的中心对称三角形DBF′，那么∠F′=∠F，FC=BF′=BE，∠F′=∠F=∠BED=∠FEA．∵∠BAC=2∠F．26.解：①在图4中可以经过旋转90∘使△ABE变到△ADF的位置．②由全等变换的定义可知，经过旋转90∘，△ABE变到△ADF的位置，只改动位置，不改动外形大小，∵△ABE≅△ADF．∵BE=DF，∠ABE=∠ADF．∵∠ADF+∠F=90∘，∵∠ABE+∠F=90∘，∵BE⊥DF．。

人教版九年级数学上册第二十三章《旋转》测试题（含答案）一．选择题1．下面生活中的实例，不是旋转的是（）A．传送带传送货物B．螺旋桨的运动C．风车风轮的运动D．自行车车轮的运动2．下列图形绕某点旋转90°后，不能与原来图形重合的是（）A．B．C．D．3．已知点A的坐标为（2，3），O为坐标原点，连接OA，将线段OA绕点A按顺时针方向旋转90°得AB，则点B的坐标为（）A．（5，1）B．（﹣3，2）C．（﹣1，5）D．（3，﹣2）4．下列说法中错误的是（）A．成中心对称的两个图形全等B．成中心对称的两个图形中，对称点的连线被对称轴平分C．中心对称图形的对称中心是对称点连线的中心D．中心对称图形绕对称中心旋转180°后，都能与自身重合5．下列英语单词中，是中心对称图形的是（）A．SOS B．CEO C．MBA D．SAR6．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．7．在平面直角坐标系中，点M（3，﹣5）关于原点对称的点的坐标是（）A．（﹣3，﹣5）B．（3，5）C．（5，﹣3）D．（﹣3，5）8．第24届冬季奥林匹克运动会，将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（）A．B．C．D．9．将图绕中心按顺时针方向旋转60°后可得到的图形是（）A．B．C．D．10．如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝15，将△ABC绕点B顺时针旋转60°，得到△BDE，连接DC交AB于点F，则△ACF与△BDF的周长之和为（）A．48B．50C．55D．60二．填空题11．与电子显示的四位数6925不相等，但为全等图形的四位数是．12．若数字串“000”和数字串“101”既是轴对称图形，又是中心对称图形，那么数字串“110”是图形（填写“轴对称”、“中心对称”）．13．如图，在△ABC中，AB＝4，AC＝3，∠BAC＝30°，将△ABC绕点A逆时针旋转60°得到△AB1C1，连接BC1，则BC1的长为．14．如图，是4×4正方形网格，其中已有4个小方格涂成了黑色，现在要从其余12个白色小方格中选出一个也涂成黑色，使整个黑色部分图形构成轴对称图形，这样的白色小方格有个．15．如图，△ABC与△DEF关于O点成中心对称．则AB DE，BC∥，AC＝．16．在平面直角坐标系中，点（﹣3，4）关于原点对称的点的坐标是．17．时钟从上午9时到中午12时，时针沿顺时针方向旋转了度．18．时钟的时针在不停地转动，从上午6时到上午9时，时针旋转的旋转角为度，从上午9时到下午5时时针旋转的旋转角为度．19．如图，把这个“十字星”形图绕其中心点O旋转，当至少旋转度后，所得图形与原图形重合．20．如图，在平面直角坐标系中，点P1的坐标为（，），将线段OP1绕点O按顺时针方向旋转45°，再将其长度伸长为OP1的2倍，得到线段OP2；又将线段OP2绕点O按顺时针方向旋转45°，长度伸长为OP2的2倍，得到线段OP3；如此下去，得到线段OP4，OP5，…，OP n（n为正整数），则点P2020的坐标是．三．解答题21．在14×9的方格纸中，每个小正方形的边长都为1，△ABC与△A′B′C′的位置如图所示；（1）请说明△ABC与△A′B′C′的位置关系；（2）若点C的坐标为（0，0），则点B′的坐标为；（3）求线段CC′的长．22．如图所示的图形是一个轴对称图形，且每个角都是直角，小明用n个这样的图形，按照如图（2）所示的方法玩拼图游戏，两两相扣，相互间不留空隙．（1）用含a、b的式子表示c；（2）当n＝2时，求小明拼出来的图形总长度；（用含a、b的式子表示）（3）当a＝4，b＝3时，小明用n个这样的图形拼出来的图形总长度为28，求n的值．23．（1）计算：+﹣2﹣1；（2）一串有趣的图案按一定规律排列．请仔细观察，按此规律画出的第10个图案是；在前16个图案中有个；第2008个图案是．24．在△ABC中，∠B+∠ACB＝30°，AB＝4，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点，如图（1）指出旋转中心，并求出旋转角的度数．（2）求出∠BAE的度数和AE的长．25．在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角．例如：正方形绕着它的对角线的交点旋转90°后能与自身重合（如图），所以正方形是旋转对称图形，它有一个旋转角为90度．（1）判断下列命题的真假（在相应的括号内填上“真”或“假”）．①等腰梯形是旋转对称图形，它有一个旋转角为180度．（）②矩形是旋转对称图形，它有一个旋转角为180°．（）（2）填空：下列图形中，是旋转对称图形，且有一个旋转角为120°的是（写出所有正确结论的序号）：①正三角形；②正方形；③正六边形；④正八边形．（3）写出两个多边形，它们都是旋转对称图形，都有一个旋转角为72°，并且分别满足下列条件：①是轴对称图形，但不是中心对称图形：；②既是轴对称图形，又是中心对称图形：．26．在平面直角坐标系中，O为原点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转，得△A′BO′，点A、O旋转后的对应点为A′、O′，记旋转角为a．（1）如图1，若a＝90°，求AA′的长；（2）如图2，若a＝120°，求点O′的坐标．参考答案一．选择题1．解：传送带传送货物的过程中没有发生旋转．故选：A．2．解：A、绕它的中心旋转90°能与原图形重合，故本选项不合题意；B、绕它的中心旋转90°能与原图形重合，故本选项不合题意；C、绕它的中心旋转90°能与原图形重合，故本选项不合题意；D、绕它的中心旋转120°才能与原图形重合，故本选项符合题意．故选：D．3．解：如图，过A作y轴的平行线，过B作x轴的平行线，交点为C，由∠C＝∠ADO，∠BAC＝∠AOD，AB＝OA，可得△ABC≌△OAD，∴AC＝OD＝2，BC＝AD＝3，∴CD＝5，点B离y轴的距离为：3﹣2＝1，∴点B的坐标为（﹣1，5），故选：C．4．解：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形与另一个图形重合，那么就说明这两个图形的形状关于这个点成中心对称，中心对称图形的对称中心是对称点连线的交点，根据中心对称图形的定义和性质可知A、C、D正确，B错误．故选：B．5．解：是中心对称图形的是A，故选A．6．解：A、是轴对称图形，不是中心对称图形，故本选项不符合题意；B、既是轴对称图形，又是中心对称图形，故本选项符合题意；C、不是轴对称图形，是中心对称图形，故本选项不符合题意；D、不是轴对称图形，是中心对称图形，故本选项不符合题意．故选：B．7．解：点M（3，﹣5）关于原点对称的点的坐标是（﹣3，5），故选：D．8．解：A、是轴对称图形，故此选项错误；B、是轴对称图形，故此选项错误；C、是轴对称图形，故此选项错误；D、不是轴对称图形，故此选项正确；故选：D．9．解：将图绕中心按顺时针方向旋转60°后得到的图形是．故选：A．10．解：∵将△ABC绕点B顺时针旋转60°，得到△BDE，∴△ABC≌△BDE，∠CBD＝60°，∴BD＝BC＝15，∴△BCD为等边三角形，∴CD＝BC＝BD＝15，∵AB＝＝＝17，∴△ACF与△BDF的周长之和＝AC+AF+CF+BF+DF+BD＝AC+AB+CD+BD＝8+15+15+17＝55，故选：C．二．填空题11．答：5269．12．解：根据对称图形的概念，知110仅是轴对称图形，对称轴为正中水平直线．13．解：∵将△ABC绕点A逆时针旋转60°得到△AB1C1，∴AC＝AC1＝3，∠CAC1＝60°，∴∠BAC1＝90°，∴BC1＝＝＝5，故答案为：5．14．解：如图所示：1，2，3位置即为符合题意的答案．故答案为：3．15．解：∵△ABC与△DEF关于O点成中心对称∴△ABC≌△DEFAB＝DE，AC＝DF又∵BO＝OE，CO＝OF，∠BOC＝∠FOE∴△BOC≌△EOF∴∠BCO＝∠OFEBC∥EF故填：＝，EF，DF16．解：点（﹣3，4）关于原点对称的点的坐标是（3，﹣4）．故答案为：（3，﹣4）．17．解：从上午9时到中午12时，时针就从指向9，旋转到指向12，共顺时针转了3个“大格”，而每个“大格”相应的圆心角为30°，所以，30°×3＝90°，故答案为：90．18．解：从上午6时到上午9时时针转过3个大格，所以，3×30°＝90°，上午9时到下午5时时针转过8个大格，所以，8×30°＝240°．故答案为：90；240．19．解：把这个“十字星”形图绕其中心点O旋转，当至少旋转360°÷4＝90°后，所得图形与原图形重合，故答案为：90．20．解：∵点P1的坐标为（，），将线段OP1绕点O按顺时针方向旋转45°，再将其长度伸长为OP1的2倍，得到线段OP2；∴OP1＝1，OP2＝2，∴OP3＝4，如此下去，得到线段OP4＝23，OP5＝24…，∴OP n＝2n﹣1，由题意可得出线段每旋转8次旋转一周，∵2020÷8＝252…4，∴点P2020的坐标与点P4的坐标在同一直线上，正好在y轴的负半轴上，∴点P2020的坐标是（0，﹣22019）．故答案为：（0，﹣22019）．三．解答题21．解：（1）△ABC与△A′B′C′成中心对称；（2）根据点C的坐标为（0，0），则点B′的坐标为：（7，﹣2）；（3）线段CC′的长为：＝2．22．解：（1）由图（1）可得，c＝；（2）观察图形可知：当2个图（1）拼接时，总长度为：2a﹣2c＝2a﹣2×＝a+b；（3）结合（2）发现：用n个这样的图形拼出来的图形总长度为：a+（n﹣1）b，当a＝4，b＝3时，4+3（n﹣1）＝28，解得：n＝9．∴n的值为9．23．解：（1）原式＝＝2；（2）根据分析，知应分别为，5，．24．解：（1）在△ABC中，∵∠B+∠ACB＝30°，∴∠BAC＝150°，当△ABC逆时针旋转一定角度后与△ADE重合，∴旋转中心为点A，∠BAD等于旋转角，即旋转角为150°；（2）∵△ABC绕点A逆时针旋转150°后与△ADE重合，∴∠DAE＝∠BAC＝150°，AB＝AD＝4，AC＝AE，∴∠BAE＝360°﹣150°﹣150°＝60°，∵点C为AD中点，∴AC＝AD＝2，∴AE＝2．25．解：（1）等腰梯形必须旋转360°才能与自身重合；矩形旋转180°可以与自身重合．①等腰梯形是旋转对称图形，它有一个旋转角为180度．（假）②矩形是旋转对称图形，它有一个旋转角为180°．（真）（2）①只要旋转120°的倍数即可；②只要旋转90°的倍数即可；③只要旋转60°的倍数即可；④只要旋转45°的倍数即可．故是旋转对称图形，且有一个旋转角为120°的是①、③．（3）360°÷72°＝5．①是轴对称图形，但不是中心对称图形：如正五边形，正十五边形；②既是轴对称图形，又是中心对称图形：如正十边形，正二十边形．26．解：（1）∵点A（4，0），点B（0，3），∴OA＝4，OB＝3．在Rt△ABO中，由勾股定理得AB＝5．根据题意，△A′BO′是△ABO绕点B逆时针旋转900得到的，由旋转是性质可得：∠A′BA＝90°，A′B＝AB＝5，∴AA′＝5．（2）如图，根据题意，由旋转是性质可得：∠O′BO＝120°，O′B＝OB＝3过点O′作O′C⊥y轴，垂足为C，则∠O′CB＝90°．在Rt△O′CB中，由∠O′BC＝60°，∠BO′C＝30°．∴BC＝O′B＝．由勾股定理O′C＝，∴OC＝OB+BC＝．∴点O′的坐标为（，）．。