3力矩力偶力偶系

5．力偶系的合成与平衡条件
=
=
如同右图
有
为合力偶矩矢，等于各分
力偶矩矢的矢量和。
合力偶矩矢的大小和方向余弦
M ( Mix )2 ( Miy )2 ( Miz )2
cos M ix cos Miy cos M iz
M
M
M
空间力偶系平衡的充分必要条件是 :合力偶矩矢等 于零，即
坐标轴上的投影。
答：
m(F , F )
F (bci acj abk); b2 c2
mx (F , F )
Fbc ; b2 c2
my (F , F )
Fac ; b2 c2
mz (F , F )
Fab b2 c2
求：工件所受合力偶矩在 轴上的投影
。
解：
M x Mix M 3 M 4 cos 45 M 5 cos 45 193.1N m
例
已知：在工件四个面上同时钻5个孔，每个孔所受 切削力偶矩均为80N·m。
求：工件所受合力偶矩在 轴上的投影
。
解：
M y Miy M 2 80N m
例
已知：在工件四个面上同时钻5个孔，每个孔所受 切削力偶矩均为80N·m。
答：SH= SV=0.791S。
1-3 两相交轴夹角为（≠0），位于两 轴平面内的力F在这两轴上的投影分别为F1 和F2。试写出F的矢2
cos
)
e1
(F2
F1 sin 2
cos
)
e
2
1-4 求题1-1中力F对x、y、z三轴、CD轴、
BC轴及D点之矩。 答 ： mx(F)=16.68 Nm ， my(F)=5.76 Nm ，
解：取微元如图

a b
M o (F ) Fd F (ob ab) F (l sin h cos )
2.合力矩定理 • 力系与其合力等效，对于使物体转动的效果，这种 性质依然存在，即合力对于一点O之矩，等于各分 力对点O之矩的代数和，这一普遍规律称为合力矩 定理。可用下式表示。
式中：
§1-3 力对点之矩、力偶
一、力对点之矩 —— 力矩 1 力矩
力的转动效果由两个因素决定： 1)、力的大小与点O到力作用线 的垂直距离 2)、力使物体绕O转动的方向
式中， Mo(F)=±Fh 表示此二因素，称为 力对点之矩简称力矩 力对点之矩的实质是 力 对通过矩心且垂直于平面 的轴的矩
其中O称为矩心，h 称为力臂，力矩为代数量，力使物体绕矩心逆 时针转动时为正，顺时针为负。
例题：梁AB 受一主动力偶作用，其力偶矩M=100 Nm ，梁长l=5m ，梁的自重不计，求两支座的约束 反力。 • 解 （1）以梁为研 究对象，进行受力 分析并画出受力图 • 因系统为力偶系， 故FA必须与FB大 小相等、方向相反、 作用线平行。 • （2）列平衡方程
∑M=0
FBl - M = 0
（1）力偶无合力。 力偶不能用一个力来等效，也不能用一个力来平衡。 可以将力和力偶看成组成力系的两个基本物理量。 （2）力偶对其作用平面内任一点的力矩，恒等于其力偶矩。
2.力偶的性质
（3）力偶的等效性——作用在同一平面的两个力偶，若它 们的力偶矩大小相等、转向相同，则这两个力偶是等效的。 则可得： • 1）力偶可以在其作用面内任意移转而不改变它对物体的作 用。即力偶对物体的作用与它在作用面内的位置无关。 • 2）只要保持力偶矩不变，可以同时改变力偶中力的大小和 力偶臂的长短，而不会改变力偶对物体的作用。

目录 上页 下页 例题库 习题集
第三章 力对点之矩 力偶系
力偶系
二、力偶的等效条件和性质 力偶的等效条件(定理） 1、力偶的等效条件(定理） 两个力偶的等效条件是它们的力偶矩相等 等效条件是它们的 两个力偶的等效条件是它们的力偶矩相等 M1 M2
B
r
F1
BA
C
r
F2
CD
F1’
7
静力学篇
目录 上页 下页 例题库 习题集
第三章 力对点之矩 力偶系
动画
力对轴之矩
§2、力对轴之矩 一、定义 z Fz Fxy o d Fxy
( moment of a force about an axis )
M z = ± dFxy
F
F
从轴的正向看， 从轴的正向看， 逆时针转向为＋ 逆时针转向为＋， 顺时针转向为－ 顺时针转向为－。
设作用于刚体上的两个力偶 M 1 , M 2
F1
M1
F
' 1
M1 = {F1 , F1' } M 2 = {F2 , F2' }
F
'
F2 r M2 F ' 2
Q F = F1 + F2 ' ' ' F = F1 + F2 ' ∴ M R = {F , F }
F
M R = r × F = r × ( F1 + F2 ) = r × F1 + r × F2 = M1 + M 2
例题库 习题集
MO (FR ) = ∑MO (Fi )
i =1
n
h
α = 20
O
MO(F) = MO(Fx ) + MO(Fy )

O x h
r
A(x,y,z) y
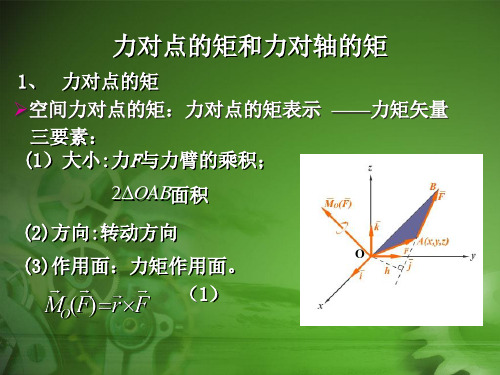
3.3 力对点之矩与力对轴之矩
3.3.1力对点之矩 以r表示力作用点A的矢径 (1)矢量积的模为
MO(F) z B
F
A(x,y,z) y
rF


rF sin Fh
k
它与力F对O点之矩矢 M o (F ) 的模相 O j 等；矢量积的方位由矢量r与F所决定 x i h 平面的垂线确定；矢量积的指向根 据矢量积规则确定，它们分别以力F 对O点之矩矢的方位和指向一致。所 以： M O (F ) r F
r
3.3 力对点之矩与力对轴之矩
3.3.1力对点之矩
z B
（2）力对点之矩矢的解析表示式 MO(F) M O (F ) r F 以矩心O为原点建立坐标系，则 k r r xi y j z k O j i h F Fx i Fy j Fz k x i j k M O (F ) r F = x y z Fx Fy Fz ( yFz zFy )i ( zFx xFz ) j ( xFy yFx )k
M1 F1d1 F3d F F3 F4
M 2 F2d(F ,F4)， M (F , F' ) M12 F'1 d 1 2 2 2 F F3 F4
M Fd ( F3 F4 )d F3d F4d M1 M 2
在同平面内的任意个力偶可以合成为一个合力偶， 合力偶矩等于各个力偶矩的代数和。 n
解：1、研究对象二力杆：AD RC N AD
RB
练习：
2、研究对象： 整体 m N AD RB l 思考：CB杆受力情况如何？

F
F d m O (F )
B A
d F'
由于O点是任取的
x
O
m F d
+
—
性质3：力偶不能简化为一个力，即力偶不能用一个力等效替
代。因此力偶不能与一个力平衡，力偶只能与力偶平衡。
力偶的作用效果取决于三个因素：构成力偶的力、 力偶臂的大小、力偶的转向。 故在平面问题中用一带箭头的弧线来表示如图所求， 其中箭头表示力偶的转向，m表示力偶矩的大小 m表 示。
即:
mi 0
i 1
n
例：三铰拱 AC 的部分上作用有力偶，其力偶矩为 M 。已知 两个半拱的直角边成正比，即 a : b = c : a ，不计三铰拱自重，求 A、B 两点的约束力。
解：各杆受力图如图，由几何关系可得FA 、FC 垂直于AC 。建立平衡方程
M
解得：
FA
0:
M FA
+
-
说明：
①
M O ( F )是代数量。
② 影响转动的独立因素。 M 当F=0或d=0时， O ( F ) =0。
④单位Nm。 ⑤
M O (F )
=2⊿AOB=Fd ,2倍⊿形面积。
在平面问题中，力对点之矩只取决于力矩的大小及其旋 转方向（力矩的正负），因此可以视为代数值。
通常规定：力偶使物体逆时针方向转动时，力偶矩为正，反 之为负（与力矩符号的规定相同）。在国际单位制中，力矩 的单位是牛顿•米（N•m）或千牛•米（kN•m）。
说明：
①力偶矩m是代数量，有+、-；
②F、 d 都不独立，只有力偶矩
③m的值：m=±2⊿ABC ； ④单位：N• m
m F d 是独立量；

根据静力学的原理，当一个物体在平面力偶的作用下处于平衡状态时，其合力矩必须为零。
平面力偶由两个大小相等、方向相反、作用线重合的平行力组成，其合力矩等于两力与两力之间的距离的乘积。
平面力偶平衡方程的应用
平面力偶平衡方程的应用主要涉及确定物体在平面力偶作用下的平衡位置。 通过将物体的重力、支持力和已知力矩表示为未知数的函数，可以建立平面力偶平衡方程并求解未知数。 求解平面力偶平衡方程时，需要利用代数方法，如加减消元法、代入法等。
力矩具有方向性，遵循右手定则。
力矩的简化表示
力矩可以表示为代数和，即所有力和力臂的乘积相加。
1
力矩可以用矢量表示，包括大小和方向。
2
力矩可以用单位表示，例如牛顿·米（N·m）。
3
在某些情况下，力矩可以简化为更简单的形式，例如在某些坐标系中。
4
02
平面力偶系
平面力偶的定义
表示方法
定义
用实线表示主动力，用虚线表示反作用力，箭头指向表示力的方向。
平面力偶的性质
合成规则
合成结果
合成结果的应用
平面力偶系的合成
合成的力偶大小等于各分力偶大小之和，方向与各分力偶方向相同或相反，取决于各分力偶的方向是相同还是相反。
通过平面力偶系的合成，可以求出作用于刚体的总力偶，从而进一步分析刚体的平衡状态和运动状态。
当有多个平面力偶作用于同一刚体时，这些力偶可以按照平行四边形法则进行合成。合成结果是一个单一的力偶，其大小和方向由合成规则确定。
平面力偶是两个大小相等、方向相反、作用线重合的平行力，它们不在同一直线上。
力偶无合力
力偶无作用点
力偶无转动中心
平面力偶由两个大小相等、方向相反的力组成，它们在同一直线上但不在同一点上，因此无法合成一个合力。

院 汽 车教 研 室
机械基础CAI课件
故力偶（ F , F ‘ ）对矩心 O 的矩为 Mo ( F ) + Mo ( F ' ）=F ( d + x ）一 Fx = Fd 上式右边为正值，说明两力矩的代数和使刚体逆时针转动，与 该力偶驱使刚体转动的转向一致。上式说明：力偶对其作用面内任 意一点的矩为一恒定代数量，该量称为力偶矩，它表示力偶对物体 转动的作用效果。 由上述可知:力偶矩是代数量，其绝对值等于力偶中的一力的 大小与力偶臂的乘积，其正负号确定如下：力偶使物体逆时针转动 为正，反之为负。力偶对其作用平面内任意 一点的矩恒等于力偶 矩。用 M 表示力偶矩，可得 M =士 Fd (3-3) 力偶矩的单位与力矩的单位相同。
图 3-4
汽 车 学 院 汽 车教 研 室
机械基础CAI课件
由式（ 3 -2 ）可得 Mo ( F ) = MO ( Fx ) + MO ( Fy ) = Fxb + Fya = F ( bsina + acosa ) ( 2 ）求力 F 对点 B 的矩。同理可得（注意分力 Fx 通过 B 点） MB ( F ) = MB ( Fx ) + MB ( Fy ) = 0 + (-Fyc）= -Fccos a
图3-5
图3-6
汽 车 学 院 汽 车教 研 室
图3-7
机械基础CAI课件
二、力偶矩 由上节已知，力使物体绕某点转动的效果用力矩来度量。同理， 力偶使物体转动的作用效果，可由组成力偶的两力对某一点的矩的 代数和来度量。 设刚体上作用有力偶（ F , F ‘ ) ，如图 3- 9 所示。在图面内任 取一点 O 为矩心，由图可见 MO ( F ) = F ( d + x ) F MO ( F ‘ ) ＝- F ′ x A 式中 d 为力偶臂。 F′ B 因 F 二 F ‘ ，可得 d MO ( F ‘ ) ＝-F , x =一 Fx O x

m0 ( F ) = ± Fd
单位：牛-米(N-m)， 千牛-米(KN-m) 性质：
单位 1。当力沿其作用线移动时，力对点之矩不变
2。当力等于零或力作用线通过矩心时，力对点之矩 为零。
§3–1 力对点之矩
二、 力对点之矩的矢积式与解析式
m0 ( F ) = r × F
其中：
r = xi + yj + zk
小结
1、理解力偶和力偶矩的概念，并运用平衡条件 求解力偶系的平衡问题
作业 3—2、 4、 9
z
′ F2
F2 F3
O y
z
l1 l2
x
45° 45°
l3
y
F1
F3′ F1′
O
解：
x
1、画出各力偶矩矢。 2、合力偶矩矢的投影：
§3-3 力偶系的合成与平衡
L x = l1 x + l2 x + l3 x = 0
L y = L1 y + l 2 y + l3 y = 0 − 10 − 30 cos 45 ° = 11 .2 N ⋅ m
Lz = l1z + l2 z + l3 z = 20 + 0 + 30 cos 45° = 41.2 N ⋅ m
3、合力矩矢L的大小和方向：
2 2 2 L = l x + l y + l z = 42.7 N ⋅ m
z
cos(L, i ) =
cos(L, j ) =
Ly L
Lx = 0, L
= 0.262 ,
NO
SBA
B
l2
α ND
D
§3-3 力偶系的合成与平衡

两端乘以OA得YROA＝Y1OA＋Y2OA＋…＋YnOA
将式（1）代入得
Mo(FR)＝Mo(F1)＋Mo(F2)＋…＋Mo(Fn)
即Mo(FR)＝ΣMo(F)
上式称为合力矩定理。合力矩定理建立了合力对点之矩与分力对同一点之矩的关系。这个定理也适用于有合力的其它力系。
例题3-2：试计算图3-4中力对A点之矩。
由经验可知，螺母能否旋动，不仅取决于作用在扳手上的力F的大小，而且还与点O到F的作用线的垂直距离d有关。因此，用F与d的乘积不作为力F使螺母绕点O转动效应的量度。其中距离d称为F对O点的力臂，点O称为矩心。由于转动有逆时针和顺时针两个转向，则力F对O点之矩定义为：力的大小F与力臂d的乘积冠以适当的正负号，以符号Mo(F)表示，记为
（3）力的大小等于零或其作用线通过矩心时，力矩等于零。
例题3-1：简支刚架如图3-2所示，荷载F=15kN，α=45。,尺寸如图。试分别计算F对A、B两点之矩。
图3-2
解：1、力F对A点的力矩
2、力F对B点的力矩
注意：负号必须标注，正号可标也可不标。一般不标注。
练习：求图（a）、（b）中荷载对A、B两点之矩
图3-4
解：本题有两种解法。
（1）由力矩的定义计算力F对A点之矩。
先求力臂d。由图中几何关系有：
d=ADsinα=(AB-DB)sinα=(AB-BCctgα)sinα
=(l-bctgα)sinα=lsinα-bcosα
所以MA(F)=F•d=F(lsinα-bcosα)
（2）根据合力矩定理计算力F对A点之矩。
教案
执教者
科目
工程力学
班级
课题
3力矩平面力偶系（一）
课型
讲授

M （ F） rAO F x O
i
j y
k z
Fx Fy Fz ( yFz zFy )i ( zFx xFz ) j ( xFy yFx ) k
结论：力矩矢在坐标轴上的投影 M 0 (F ) x M x (F ) M 0 (F ) y M y (F ) M 0 (F ) z M z (F )
§ 3-2 力偶及其性质 力偶系的合成与平衡 一、力偶( F , F)
由大小相等,方向相反而不共线 的两个平行力组成的力系。
F d
B A
F= - F
F´
力偶只能使物体发生转动， 不引起移动。
二、力偶矩
F
1、平面力系：
d
A
B
m = ±Fd
正负号的规定： 力偶使物体逆时针转为 + 力偶使物体顺时针转为– 2、空间力系：力偶矩是一个矢量
m
F´
M
A F
M rBA F
rBA
F´
B
三、力偶的性质
1、力偶不能与一个力等效，因此力偶没有合力，也不能
用一个力来平衡。力偶只能与力偶等效,也只能与力 偶平衡。
2、力偶中两力对空间任一点的矩的矢量和（代数和） 等于该力偶矩 ,而与矩心的选择无关。
m mo(F) +mo(F´) = rB0×F + rA0× F´ = rBA×F
d
a
Fxy b
z
结论:
F
B
(a) 当力的作用线与轴平行或相交，
A
即力与轴位于同一平面时力对轴
之矩等于零；
o
(b) 当力沿其作用线移动时力 矩不变。