第6章 Matlab平面连杆机构的动力学分析

六杆机构的动力学分析仿真一系统模型建立为了对机构进行仿真分析，首先必须建立机构数学模型，即位置方程，然后利用MATLAB仿真分析工具箱Simulink对其进行仿真分析。

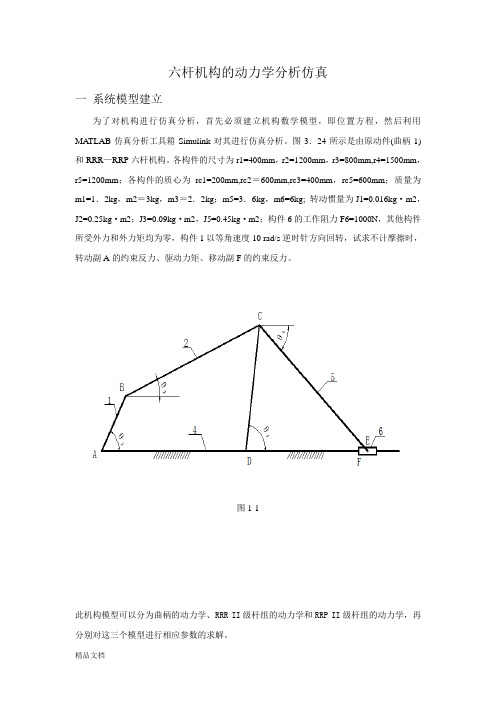
图3．24所示是由原动件(曲柄1)和RRR—RRP六杆机构。

各构件的尺寸为r1=400mm，r2=1200mm，r3=800mm,r4=1500mm，r5=1200mm；各构件的质心为rc1=200mm,rc2＝600mm,rc3=400mm，rc5=600mm；质量为m1=1．2kg，m2＝3kg，m3＝2．2kg；m5=3．6kg，m6=6kg; 转动惯量为J1=0.016kg·m2，J2=0.25kg·m2；J3=0.09kg·m2，J5=0.45kg·m2；构件6的工作阻力F6=1000N，其他构件所受外力和外力矩均为零，构件1以等角速度10 rad/s逆时针方向回转，试求不计摩擦时，转动副A的约束反力、驱动力矩、移动副F的约束反力。

图1-1此机构模型可以分为曲柄的动力学、RRR II级杆组的动力学和RRP II级杆组的动力学，再分别对这三个模型进行相应参数的求解。

图1-2 AB 构件受力模型如上图1-2对于曲柄AB 由理论力学可以列出表达式：111XA Re R ••=+-s m F R X XB 111y A Im R ••=+-s m F R y yB1111111111111cos )(sin )(cos sin ••=---+-++θθθθθJ r r R r r R r R r R M M c yB c XB c yA c XA F由运动学知识可以推得：)cos()2/cos(Re Re 12111111πθθπθθ++++=•••••••c c r r A s )sin()2/sin(Im Im 12111111πθθπθθ++++=•••••••c c r r A s将上述各式合并成矩阵形式有，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+++++-++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡••••••••••g m R F r m r m A m R F r m r m A m M R R yB y c c XBX c c yA XA 111211111111112111111111)sin()2/sin(Im )cos()2/cos(Re πθθπθθπθθπθθ(1-21)如图1-3，对构件BC 的约束反力推导如下，图1-3 BC 构件受力模型222Re ••=++s m R F R XC X XB 2222Im ••=-++s m g m R F R yC y yB2222222222222cos )(sin )(cos sin ••=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yB c XB如图1-4，对构件BC 的约束反力推导如下，图 1-4 CD 构件受力模型333Re ••=-+s m R F R XC X XD 3333Im ••=-++s m g m R F R yC y yD3333333333333cos )(sin )(cos sin ••=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yD c XD由运动学可以推导得，)sin()2/sin(Im Im 22222222πθθπθθ++++=•••••••c c r r B s )cos()2/cos(Re Re 22222222πθθπθθ++++=•••••••c c r r B s )cos()2/cos(Re Re 32333333πθθπθθ++++=•••••••c c r r D s )sin()2/sin(Im Im 32333333πθθπθθ++++=•••••••c c r r D s将上述BC 构件，CD 构件各式合并成矩阵形式有，⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------33333333332222222222cos sin cos )(sin )(0010100001010000cos )(sin )(cos sin 001010000101θθθθθθθθc c c c c c c c r r r r r r r r r r r r ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡yD XD yC XC yB XB R R R R R R =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+-++++-++++-+-++++-++++••••••••••••••••••••••••3333332333333333323333333322222222222222222222222222)sin()2/sin(Im )cos()2/cos(Re )sin()2/sin(Im )cos()2/cos(Re M J g m F r m r m D m F r m r m D m M J g m F r m r m B m F r m r m B m y c c X c c y c c X c c θπθθπθθπθθπθθθπθθπθθπθθπθθ (1-22)如图1-5 对构件5进行约束反力的推导如下，图1-5 CE 杆件受力模型••=++s m R F R xE x xC Re 55 ••=-++s m g m R F R yE y yC Im 5555555555555555cos )(sin )(cos sin ••=-+-+--θθθθθJ r r R r r R r R r R M c yE c xE c yC c xC如图1-6 对滑块进行受力分析如下，滑块受力模型••=--E m R R F F xE x Re sin 666θ ••=-+-E m g m R R F F yE y Im cos 6666θ由运动学可推，)cos()2/cos(C Re Re 5255555πθθπθθ•••••••+++=c c r r s )sin()2/sin(C Re Im 5255555πθθπθθ•••••••+++=c c r r s66cos Re θ••••=s E 66sin Im θ••••=s E⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+---+-++++-++++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------••••••••••••••••g m F s m F s m M J g m F r m r m m F r m r m m R R R R R r r r r r r y x y c c x c c F yE xE yC xC c c c c 66666666655555525555555555255555555665555555555sin cos )sin()2/sin(C Re )cos()2/cos(C Re cos 1000sin 01000cos )(sin )(cos sin 010*******θθθπθθπθθπθθπθθθθθθθθ（1-23）二编程与仿真利用MATLAB进行仿真分析，主要包括两个步骤：首先是编制计算所需要的函数模块，然后利用其仿真工具箱Simulink建立仿真系统框图，设定初始参数进行仿真分析。

基于MATLAB的平面连杆机构运动分析及动画摘要建立了平面机构运动分析的数学模型，利用MATLAB进行了编程并设计了计算交互界面进而求解，为解析法的复杂计算提供了便利的方法，此方法也同样适用于复杂平面机构的运动分析，并为以后机构运动分析的通用软件的设计提供了基础。

建立了平面四杆机构运动分析的数学模型，以MATLAB 程序设计语言为平台，将参数化设计与交互式相结合，设计了平面四杆机构仿真软件，该软件具有方便用户的良好界面，并给出界面设计程序，从而使机构分析更加方便、快捷、直观和形象。

设计者只需输入参数就可得到仿真结果，再将运行结果与设计要求相比较，对怎样修改设计做出决策，它为四杆机构设计提供了一种实用的软件与方法。

以一种平面六连杆为例建立了平面多连杆机构的运动分析数学模型，应用MATLAB 软件进行了优化设计和仿真分析，为机构优化设计提供了一种高效、直观的仿真手段，提高了对平面多连杆机构的分析设计能力。

同时，也为其他机构的仿真设计提供了借鉴。

关键词：解析法，平面连杆机构，MATLAB，运动分析，运动仿真Based on the MATLAB Planar Linkage Mechanism MotionAnalysis and AnimationABSTRACTThis article established the kinematical mathematic model of the planar mechanism ,which is programmed and solved with designing the mutual interface of the calculation by MATLAB.This convenient method is provided for the complicated calculation of the analysis and also applicable to the kinematical analysis of the complex planar mechanism.A mathematical model of motion analysis was established in planar four- linkage ,and emulational software was developed. The software adopted MATLAB as a design language. It combined parametric design with interactive design and had good interfacefor user. Thus,it was faster and more convenient to analyse linkage. The emulational result was obtained as soon as input parameters was imported and the devisers can make decision-making of modification by the comparing emulational result with design demand. It provides an applied software and method for linkage.This paper took a planar six-linkage mechanism as a example to set up the mathematics model of planar multi-linkage mechanisms, and made the optimization design and simulation by the MATLAB software. It gave a efficiently and directly method to optimization design of mechanisms, and improved the ability of analyzing and designing the planar multi-linkage mechanisms. At the same time, it also provides a use for reference to the design and simulation for other mechanisms.KEY WORDS: analysis, planar linkage mechanisms, MATLAB, kinematical analysis, kinematical simulation目录1.1 平面连杆机构的研究意义 (1)1.2 平面连杆机构的研究现状 (1)1.3 MATLAB软件介绍 (2)1.3.1 MATLAB简介 (2)1.3.2 MATLAB软件的特点 (4)1.3.3 用MATLAB处理工程问题优缺点 (5)第2章平面机构运动分析的复数矢量解 (6)第3章平面四杆机构运动分析 (8)3.1 铰链四杆机构曲柄存在条件 (8)3.2 平面四杆机构的位移分析 (9)3.3 平面四杆机构的速度分析 (14)3.4 平面四杆机构的加速度分析 (15)第4章基于MATLAB的平面四杆机构运动分析 (17)4.1 基于MATLAB的平面四杆机构运动参数输入界面 (17)4.2 基于MATLAB的平面四杆机构运动参数计算 (21)4.3 基于MATLAB的平面四杆机构运动分析界面 (24)4.4 基于MATLAB的平面四杆机构运动仿真 (26)4.5 基于MATLAB的平面四杆机构运动参数清空及退出 (30)第5章平面六杆机构运动分析 (32)5.1 构建平面六杆机构数学模型 (32)5.2 平面六杆机构的运动分析 (33)5.2.1 曲柄导杆机构的运动分析 (33)5.2.2 摆动滑块机构的运动分析 (36)第6章基于MATLAB的平面六杆机构运动分析 (39)6.1 基于MATLAB的平面六杆机构运动参数输入界面 (39)6.2 基于MATLAB的平面六杆机构运动参数计算 (45)6.3 基于MATLAB的平面六杆机构运动分析界面 (49)6.4 基于MATLAB的平面六杆机构运动仿真 (52)6.5 基于MATLAB的平面六杆机构运动参数清空及退出 (56)结论 (57)参考文献 (59)第1章前言1.1 平面连杆机构的研究意义机构运动分析是不考虑引起机构运动的外力的影响，而仅从几何角度出发，根据已知的原动件的运动规律（通常假设为匀速运动），确定机构其它构件上各点的位移、速度、加速度，或构件的角位移、角速度、角加速度等运动参数。

1平面连杆机构的运动分析1。

1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构，它可以用来实现转动和摆动之间运动形式的转换或传递动力。

对四杆机构进行运动分析的意义是:在机构尺寸参数已知的情况下，假定主动件（曲柄)做匀速转动，撇开力的作用,仅从运动几何关系上分析从动件(连杆、摇杆）的角位移、角速度、角加速度等运动参数的变化情况。

还可以根据机构闭环矢量方程计算从动件的位移偏差。

上述这些内容，无论是设计新的机械，还是为了了解现有机械的运动性能，都是十分必要的，而且它还是研究机械运动性能和动力性能提供必要的依据.机构运动分析的方法很多，主要有图解法和解析法。

当需要简捷直观地了解机构的某个或某几个位置的运动特性时,采用图解法比较方便，而且精度也能满足实际问题的要求。

而当需要精确地知道或要了解机构在整个运动循环过程中的运动特性时,采用解析法并借助计算机，不仅可获得很高的计算精度及一系列位置的分析结果，并能绘制机构相应的运动线图，同时还可以把机构分析和机构综合问题联系起来，以便于机构的优化设计.1。

2 机构的工作原理在平面四杆机构中，其具有曲柄的条件为:a.各杆的长度应满足杆长条件，即：最短杆长度+最长杆长度≤其余两杆长度之和。

b。

组成该周转副的两杆中必有一杆为最短杆,且其最短杆为连架杆或机架（当最短杆为连架杆时,四杆机构为曲柄摇杆机构;当最短杆为机架时，则为双曲柄机构）。

在如下图1所示的曲柄摇杆机构中，构件AB为曲柄,则B点应能通过曲柄与连杆两次共线的位置。

1.3 机构的数学模型的建立1。

3。

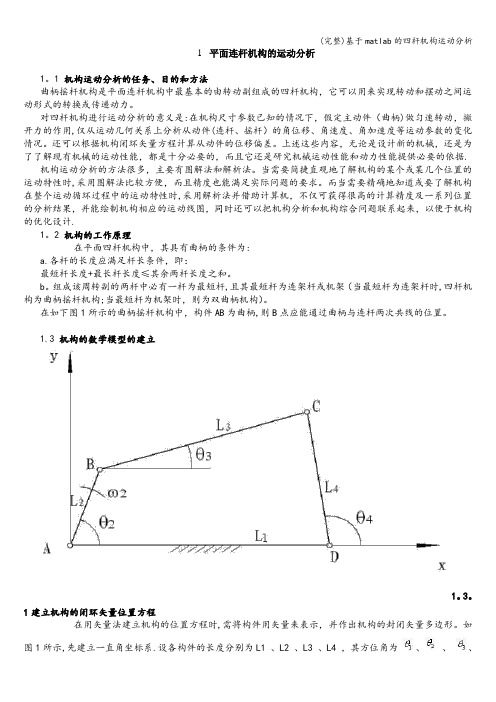
1建立机构的闭环矢量位置方程在用矢量法建立机构的位置方程时,需将构件用矢量来表示，并作出机构的封闭矢量多边形。

如图1所示,先建立一直角坐标系.设各构件的长度分别为L1 、L2 、L3 、L4 ，其方位角为、、、.以各杆矢量组成一个封闭矢量多边形，即ABCDA。

其个矢量之和必等于零。

六杆机构的动力学分析仿真一系统模型建立为了对机构进行仿真分析，首先必须建立机构数学模型，即位置方程，然后利用MATLAB 仿真分析工具箱Simulink对其进行仿真分析。

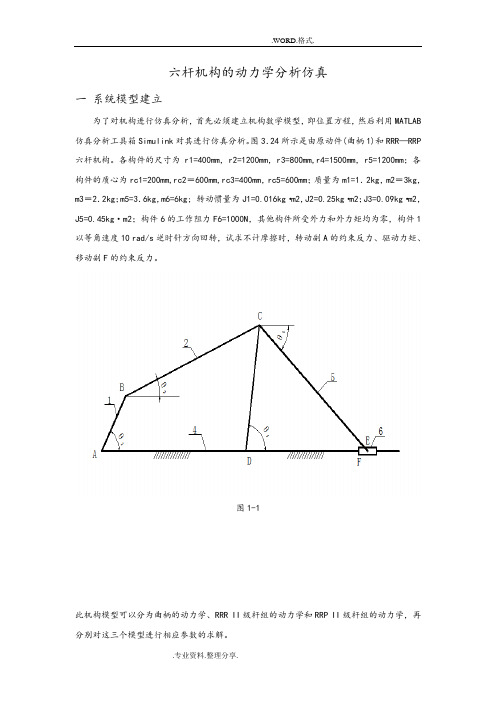
图3．24所示是由原动件(曲柄1)和RRR—RRP 六杆机构。

各构件的尺寸为r1=400mm，r2=1200mm，r3=800mm,r4=1500mm，r5=1200mm；各构件的质心为rc1=200mm,rc2＝600mm,rc3=400mm，rc5=600mm；质量为m1=1．2kg，m2＝3kg，m3＝2．2kg；m5=3．6kg，m6=6kg; 转动惯量为J1=0.016kg·m2，J2=0.25kg·m2；J3=0.09kg·m2，J5=0.45kg·m2；构件6的工作阻力F6=1000N，其他构件所受外力和外力矩均为零，构件1以等角速度10 rad/s逆时针方向回转，试求不计摩擦时，转动副A的约束反力、驱动力矩、移动副F的约束反力。

图1-1此机构模型可以分为曲柄的动力学、RRR II级杆组的动力学和RRP II级杆组的动力学，再分别对这三个模型进行相应参数的求解。

图1-2 AB 构件受力模型如上图1-2对于曲柄AB 由理论力学可以列出表达式：111XA Re R ∙∙=+-s m F R X XB 111y A Im R ∙∙=+-s m F R y yB1111111111111cos )(sin )(cos sin ∙∙=---+-++θθθθθJ r r R r r R r R r R M M c yB c XB c yA c XA F由运动学知识可以推得：)cos()2/cos(Re Re 12111111πθθπθθ++++=∙∙∙∙∙∙∙c c r r A s )sin()2/sin(Im Im 12111111πθθπθθ++++=∙∙∙∙∙∙∙c c r r A s将上述各式合并成矩阵形式有，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+++++-++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∙∙∙∙∙∙∙∙∙∙g m R F r m r m A m R F r m r m A m M R R yB y c c XBX c c yA XA 111211111111112111111111)sin()2/sin(Im )cos()2/cos(Re πθθπθθπθθπθθ(1-21)如图1-3，对构件BC 的约束反力推导如下，图1-3 BC 构件受力模型222Re ∙∙=++s m R F R XC X XB 2222Im ∙∙=-++s m g m R F R yC y yB2222222222222cos )(sin )(cos sin ∙∙=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yB c XB如图1-4，对构件BC 的约束反力推导如下，图 1-4 CD 构件受力模型333Re ∙∙=-+s m R F R XC X XD 3333Im ∙∙=-++s m g m R F R yC y yD3333333333333cos )(sin )(cos sin ∙∙=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yD c XD由运动学可以推导得，)sin()2/sin(Im Im 22222222πθθπθθ++++=∙∙∙∙∙∙∙c c r r B s )cos()2/cos(Re Re 22222222πθθπθθ++++=∙∙∙∙∙∙∙c c r r B s )cos()2/cos(Re Re 32333333πθθπθθ++++=∙∙∙∙∙∙∙c c r r D s )sin()2/sin(Im Im 32333333πθθπθθ++++=∙∙∙∙∙∙∙c c r r D s将上述BC 构件，CD 构件各式合并成矩阵形式有，⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------33333333332222222222cos sin cos )(sin )(0010100001010000cos )(sin )(cos sin 001010000101θθθθθθθθc c c c c c c c r r r r r r r r r r r r ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡yD XD yC XC yB XB R R R R R R =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+-++++-++++-+-++++-++++∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3333332333333333323333333322222222222222222222222222)sin()2/sin(Im )cos()2/cos(Re )sin()2/sin(Im )cos()2/cos(Re M J g m F r m r m D m F r m r m D m M J g m F r m r m B m F r m r m B m y c c X c c y c c X c c θπθθπθθπθθπθθθπθθπθθπθθπθθ (1-22)如图1-5 对构件5进行约束反力的推导如下，图1-5 CE 杆件受力模型∙∙=++s m R F R xE x xC Re 55 ∙∙=-++s m g m R F R yE y yC Im 5555555555555555cos )(sin )(cos sin ∙∙=-+-+--θθθθθJ r r R r r R r R r R M c yE c xE c yC c xC如图1-6 对滑块进行受力分析如下，滑块受力模型∙∙=--E m R R F F xE x Re sin 666θ ∙∙=-+-E m g m R R F F yE y Im cos 6666θ由运动学可推，)cos()2/cos(C Re Re 5255555πθθπθθ∙∙∙∙∙∙∙+++=c c r r s )sin()2/sin(C Re Im 5255555πθθπθθ∙∙∙∙∙∙∙+++=c c r r s66cos Re θ∙∙∙∙=s E 66sin Im θ∙∙∙∙=s E⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+---+-++++-++++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙g m F s m F s m M J g m F r m r m m F r m r m m R R R R R r r r r r r y x y c c x c c F yE xE yC xC c c c c 66666666655555525555555555255555555665555555555sin cos )sin()2/sin(C Re )cos()2/cos(C Re cos 1000sin 01000cos )(sin )(cos sin 010*******θθθπθθπθθπθθπθθθθθθθθ（1-23）二编程与仿真利用MATLAB进行仿真分析，主要包括两个步骤：首先是编制计算所需要的函数模块，然后利用其仿真工具箱Simulink建立仿真系统框图，设定初始参数进行仿真分析。

基于MATLAB/Solidworks COSMOSMotion的平面连杆机构动力学分析07208517王锡霖4-23在图示的正弦机构中,已知l AB =100 mm,h1=120 mm,h2 =80 mm,W1 =10 rad/s(常数)，滑块2和构件3的重量分别为G2 =40 N和G3 =100 N,质心S2 和S3 的位置如图所示，加于构件3上的生产阻力Fr=400 N，构件1的重力和惯性力略去不计。

试用解析法求机构在Φ1=60°、150°、220°位置时各运动副反力和需加于。

构件1上的平衡力偶Mb分别对三个构件进行受力分析如图：构件3受力图构件2受力图构件1受力图（1）滑块2：V S2 =L AB W1 ①a s2 = L AB W12②构件3：S=L AB sinΦ1 ③V3=L AB W1 COSΦ1 ④a3=-L AB W12 sinΦ1 ⑤(2)确定惯性力：F12=m2as2=(G2/g)LABW12 ⑥F13=m3a3=(G3/g)LABW12sinΦ1 ⑦(3)各构件的平衡方程：构件3：∑Fy=0,FR23 =Fr-F13∑Fx=0,FR4’=FR4∑MS3 =0,FR4=FR23LAcosΦ1/h2构件2：∑Fx=0,FR12x=F12cosΦ1∑Fy=0,FR12y=FR32-F12sinΦ1构件1：∑Fx=0,FR41x=FR12x∑Fy=0,FR41y=FR12y∑MA =0,Mb=FR32LABcosΦ1总共有八个方程，八个未知数。

归纳出一元八次方程矩阵：1 0 0 0 0 0 0 0 FR23 Fr-F130 1 -1 0 0 0 0 0 FR4’ 0-LAB COSΦ1/h20 1 0 0 0 0 0 FR40 0 0 1 0 0 0 0 FR12x = F12cosΦ1-1 0 0 0 1 0 0 0 FR12y -F12sinΦ10 0 0 -1 0 1 0 0 FR41x 00 0 0 0 -1 0 1 0 FR41y 0-LABCOSΦ1 0 0 0 0 0 0 1 Mb 0 AX=B进而可得：X=A\B。

构件上点的运动分析函数文件（m文件）格式：function [ 输出参数] = 函数名（输入参数）p_crank.m function [p_Nx,p_Ny]=p_crank(Ax,Ay,theta,phi,l1)v_crank.m function [v_Nx,v_Ny]=v_crank(l1,v_Ax,v_Ay,omiga,theta,phi)a_crank.m function [a_Nx,a_Ny]=a_crank(l1,a_Ax,a_Ay,alpha,omiga,theta,phi)函数中的符号说明函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）p_RRR.m function [cx,cy,theta2,theta3]=p_RRR(bx,by,dx,dy,l2,l3,m)v_RRR.m function [vcx,vcy,omiga2,omiga3]=v_RRR(vbx,vby,vdx,vdy,cx,cy,bx,by,dx,dy)a_RRR.m function [acx,acy,alpha2,alpha3]=a_RRR(abx,aby,adx,ady,cx,cy,bx,by,dx,dy,omiga2,omiga3)函数中的符号说明m =1 m = -1RRR Ⅱ级杆组运动分析函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）p_RRP.m function [cx,cy,sr,theta2]=p_RRP(bx,by,px,py,theta3,l2,m)v_RRP.m function [vcx,vcy,vr,omiga2]=v_RRP(bx,by,cx,cy,vbx,vby,vpx,vpy,theta2,theta3,l2,sr,omiga3) a_RRP.m function [acx,acy,ar,alpha2]=a_RRP(bx,by,cx,cy,px,py,abx,aby,apx,apy,theta3,vr,omiga2,omiga3,alpha3)函数中的符号说明1 1∠BCP < 90︒，∠BC 'P > 90︒，m =1RRP Ⅱ级杆组运动分析函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）p_RPR.m function [dx,dy,sr,theta3]=p_RPR(bx,by,cx,cy,e,l3,m)v_RPR.m function [vdx,vdy,omiga3,vr]=v_RPR(bx,by,cx,cy,dx,dy,vcx,vcy,vbx,vby,theta3) a_RPR.m function [adx,ady,alpha3,ar]=a_RPR(bx,by,cx,cy,dx,dy,acx,acy,abx,aby,vr,omiga3,theta3)RPR Ⅱ级杆组运动分析实线位置，m =1 虚线位置，m = -1函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）F_RRR.m function [R12x,R12y,R23x,R23y,R34x,R34y]=F_RRR(bxy,cxy,dxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,as2,as3,alpha2,alpha3)RRR Ⅱ级杆组力分析R 23xF 2R F 3xR 23函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）F_RRP.m function [R12x,R12y,R23x,R23y,R34x,R34y,lcn]=F_RRP(bxy,cxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,theta3,as2,as3,alpha2,alph3)RRP Ⅱ级杆组力分析R 34函数文件（m 文件）格式： function [ 输出参数 ] = 函数名（ 输入参数 ）F_RPR.m function [R12x,R12y,R23x,R23y,R35x,R35y,lcn]=F_RRP(bxy,cxy,dxy,s2,s3,m2,m3,Js2,Js3,M2,M3,F2,F3,R34,theta3,as2,as3,alpha3)RPR Ⅱ级杆组力分析238. 作用有平衡力的构件力分析作用有平衡力的构件力分析函数文件（m文件）格式：function [ 输出参数] = 函数名（输入参数）F_Bar.m function [R01x,R01y,Mb]=F_Bar(axy,bxy,s1,m1,Js1,M1,F1,R12,as1,alpha1)函数中的符号说明9. 平面连杆机构运动分析算例例1图示曲柄摇杆机构，已知l 1=150mm ，l 2=220mm ，l 3=250mm ，l 4=300mm ，曲柄以n 1=100r/min 逆时针匀速转动，分析该机构的运动。

平面多连杆机构动力学建模与分析研究Chapter 1 引言在机械传动领域，平面多连杆机构是一种很常见的机械结构。

由于其设计简单、性能可靠等特点，在机械制造、航空、汽车、电子等领域有着广泛的应用。

平面多连杆机构的运动学和动力学分析一直是机械设计和计算机辅助设计领域需要解决的难题之一，因此对平面多连杆机构的动力学建模与分析的研究有着重要的意义。

本文主要介绍平面多连杆机构的动力学建模与分析的研究，包括平面多连杆机构的运动学方程、动力学方程等内容。

Chapter 2 平面多连杆机构的运动学方程平面多连杆机构是由多个连接杆件连成一个复杂的梯形链条结构，运动学方程是了解机构运动状态的基础，是机构动力学建模的前提。

平面多连杆机构的运动学方程通过从机构的杆件运动状态、几何条件及运动约束方程中推导而来。

运动状态是指多连杆机构在其由静止到运动的状态，即是以不同杆件为坐标系所定义的各运动参数与系统间所建立的模型。

悬链线方程是运动学中一个重要的公式，在平面多连杆机构的运动学方程中，用来关联各个连接杆件的运动和几何参数，因此其正确性对运动学方程的推导至关重要。

运动学方程包含了平面多连杆机构四驱动链和五驱动链，它们分别包括四个和五个独立的驱动旋转关节，计算公式如下：四驱动链：$$\begin{cases}x_3=x_0+l_1cos\alpha_1+l_2cos\alpha_2+l_3cos\alpha_3\\y_3=y_0+l_1sin\alpha_1+l_2sin\alpha_2+l_3sin\alpha_3\end{cases}$$五驱动链：$$\begin{cases}x_4=x_0+l_1cos\alpha_1+l_2cos\alpha_2+l_3cos\alpha_3\\y_4=y_0+l_1sin\alpha_1+l_2sin\alpha_2+l_3sin\alpha_3\\x_5=x_2-l_4cos\alpha_4-l_5cos\alpha_5-l_6cos\alpha_6\\y_5=y_2-l_4sin\alpha_4-l_5sin\alpha_5-l_6sin\alpha_6\end{cases}$$其中，$x_i$和$y_i$表示杆件i的末端的坐标，$l_i$是杆件i的长度，$\alpha_i$表示杆件的转角。

matlab动力学分析程序详解··1.微分方程的定义对于duffing 方程032=++x x xω ，先将方程写作--==3112221x x x x x ω function dy=duffing(t,x) omega=1;%定义参数f1=x(2);f2=-omega^2*x(1)-x(1)^3; dy=[f1;f2];2.微分方程的求解function solve (tstop) tstop=500;%定义时间长度 y0=[0.01;0];%定义初始条件[t,y]=ode45('duffing',tstop,y0,[]);function solve (tstop) step=0.01;%定义步长y0=rand(1,2);%随机初始条件tspan=[0:step:500];%定义时间范围[t,y]=ode45('duffing',tspan,y0);3.时间历程的绘制时间历程横轴为t ，纵轴为y ，绘制时只取稳态部分。

plot(t,y(:,1));%绘制y 的时间历程 xlabel('t')%横轴为t ylabel('y')%纵轴为y grid;%显示网格线axis([460 500 -Inf Inf])%图形显示范围设置4.相图的绘制相图的横轴为y ，纵轴为dy/dt ，绘制时也只取稳态部分。

红色部··分表示只取最后1000个点。

plot(y(end-1000:end,1),y(end-1000:end,2));%绘制y 的时间历程xlabel('y')%横轴为yylabel('dy/dt')%纵轴为dy/dt grid;%显示网格线5.Poincare 映射的绘制对于不同的系统，Poincare 截面的选取方法也不同对于自治系统一般每过其对应线性系统的固有周期，截取一次对于非自治系统，一般每过其激励的周期，截取一次例程：duffing 方程032=++x x x ω的poincare 映射function poincare(tstop) global omega; omega=1;T=2*pi/omega;%线性系统的周期或激励的周期step=T/100;%定义步长为T/100 y0=[0.01;0];%初始条件tspan=[0:step:100*T];%定义时间范围[t,y]=ode45('duffing',tspan,y0);for i=5000:100:10000%稳态过程每个周期取一个点plot(y(i,1),y(i,2),'b.'); hold on;% 保留上一次的图形 endxlabel('y');ylabel('dy/dt');Poincare 映射也可以通过取极值点得到 function poincare(tstop) y0=[0.01;0];tspan=[0:0.01:500];[t,y]=ode45('duffing',tspan,y0); count=find(t>100);%截取稳态过程 y=y(count,:);n=length(y(:,1));%计算点的总数··for i=2:n-1if y(i-1,1)+epsy(i+1,1)+eps % 简单的取出局部最大值plot(y(i,1),y(i,2),'.'); hold on end endxlabel('y');ylabel('dy/dt');6.频谱yy=fft(y(end-1000:end,1)); N=length(yy); power=abs(yy);freq=(1:N-1)*1/step/N;plot(freq(1:N/2),power(1:N/2)); xlabel('f(y)') ylabel('y')7.算例duffing 方程03=++x x x的时间历程，相图，频谱和poincare 映射。