下载文档原格式
极限存在准则与两个重要极限首先，我们来定义极限存在准则。
设函数f(x)在x=a的其中一去心邻域内有定义，且有极限L，那么对于任意给定的正数ε，存在正数δ，使得当0<，x-a，<δ时，有，f(x)-L，<ε。
左极限：设函数f(x)在x=a的其中一左去心邻域内有定义，且有极限L，那么对于任意给定的正数ε，存在正数δ，使得当a-δ<x<a时，有，f(x)-L，<ε。
右极限：设函数f(x)在x=a的其中一右去心邻域内有定义，且有极限L，那么对于任意给定的正数ε，存在正数δ，使得当a<x<a+δ时，有，f(x)-L，<ε。
接下来，我们来介绍两个重要的极限存在准则。
1.夹逼准则（或夹挤准则）：设函数f(x)在x=a的其中一去心邻域内有定义，且在这个去心邻域中，存在两个函数g(x)和h(x)，满足g(x)≤f(x)≤h(x)。
若当x→a时，g(x)和h(x)的极限都是L，则函数f(x)在x=a处的极限也是L。
夹逼准则的直观意义是，如果一个函数在一些点附近被两个函数“夹住”，而这两个函数的极限是相等的，则原函数在该点也存在极限，并且极限等于夹逼的值。
2.单调有界准则：如果函数f(x)在x=a的其中一去心邻域内有定义，并且在这个去心邻域中是递增或递减的（即f’(x)≥0或f’(x)≤0），那么如果存在一个实数M，使得对于任意的x，都有f(x)≤M（或f(x)≥M），那么函数f(x)在x=a处存在极限。
单调有界准则的直观意义是，如果一个函数在一些点附近是单调递增或递减的，并且在该区间内被一个实数所界定，那么函数在该点存在极限。
这两个极限存在准则在微积分中具有重要的意义和应用。
在求解极限问题时，可以利用夹逼准则来确定极限的存在性。
而在证明一些极限存在的定理时，可以利用单调有界准则来进行证明。
总结起来，极限存在准则是用于确定函数在一些点是否存在极限的基本规则。
夹逼准则和单调有界准则是两个重要的应用极限存在准则，它们在微积分中有着广泛的应用。
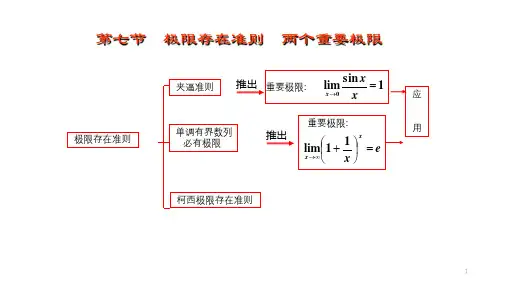
两个极限存在准则和两个重要的极限1.两个极限存在准则(1) 夹逼准则：设a, b, c为实数，如果函数f(x)在a的一些左邻域内对于一切x都有h(x)≤f(x)≤g(x)，且lim[x→a]h(x)=lim[x→a]g(x)=L，则必有lim[x→a]f(x)=L。
夹逼准则的本质是通过构造两个函数作为边界来确定原函数的极限。
(2) 单调有界准则：设函数f(x)在(a, b)上单调递增(递减)，且在(a, b)上有界，则必有lim[x→a]f(x)=sup{f(x)}(或lim[x→a]f(x)=inf{f(x)})。
单调有界准则的基本思想是通过函数的单调性和有界性来确定极限。
(1) 无穷小极限：设函数f(x)在x=a处有极限lim[x→a]f(x)=0，如果对于任意正数ε，存在对应的正数δ，使得对于所有满足0<，x-a，< δ的x，有，f(x)，<ε，那么称函数f(x)在x=a处的极限为0。
无穷小极限的重要性在于它在微积分中有广泛应用。
例如，微分定义中的导数可以看作是函数在其中一点的极限，这也符合函数在该点的变化趋势比较明显。
无穷小极限的概念使得我们能够更好地描述和理解函数在其中一点的变化情况。
(2) 无穷大极限：设函数f(x)在x=a处有极限lim[x→a]f(x)=∞，如果对于任意正数M，存在对应的正数δ，使得对于所有满足0<，x-a，< δ的x，有f(x) > M，那么称函数f(x)在x=a处的极限为无穷大。
无穷大极限的重要性在于它可以帮助我们研究函数在其中一点的增长速度和趋势。
例如，在极限定义中，我们可以通过无穷大极限来刻画函数在其中一点的无限增长或无限逼近的情况。
此外，无穷大极限也在微积分中的积分定义中有重要的应用，帮助我们理解函数的积分和面积的概念。
综上所述，极限的存在准则和重要的极限是微积分中的重要概念。
了解它们的定义和应用可以帮助我们更好地理解和分析函数在其中一点的变化情况，为进一步研究微积分和数学分析打下坚实的基础。
