201709年高考数学函数模型及其应用复习.doc
- 格式:doc
- 大小:100.68 KB
- 文档页数:4



专题06 函数与方程﹑函数模型及其应用 文1.函数f (x )=ln(x +1)-2x的零点所在的区间是( )A .(12,1) B .(1,e -1)C .(e -1,2)D .(2,e) 【答案】B【解析】因为f (12)=ln 32-4<0,f (1)=ln2-2<0,f (e -1)=1-2e -1<0,f (2)=ln3-1>0,故零点在区间(e -1,2)内.2.已知函数f (x )=(14)x-cos x ,则f (x )在[0,2π]上的零点个数是( )A .1B .2C .3D .4 【答案】C【解析】f (x )在[0,2π]上的零点个数就是函数y =(14)x和y =cos x 的图象在[0,2π]上的交点个数,而函数y =(14)x 和y =cos x 的图象在[0,2π]上的交点有3个.3.函数f (x )=⎩⎪⎨⎪⎧12x -2,x <0,x -1,x ≥0的所有零点的和等于( )A .-2B .-1C .0D .1 【答案】C【解析】令(12)x-2=0,解得x =-1,令x -1=0,解得x =1,所以函数f (x )存在两个零点1和-1,其和为0.4.若函数f (x )=x 2+2a |x |+4a 2-3的零点有且只有一个,则实数a 等于( ) A.32或-32 B .-32 C.32D .以上都不对【答案】C5.定义在R 上的函数f (x )满足f (x +4)=f (x ),f (x )=⎩⎪⎨⎪⎧-x 2+1,-1≤x ≤1,log 2-|x -2|+,1<x ≤3.若关于x 的方程f (x )-ax =0有5个不同实根,则正实数a 的取值范围是( ) A .(14,13) B .(16,14)C .(16-67,16)D .(16,8-215)【答案】D【解析】f (x )是周期为4的周期函数.做出y =f (x )和y =ax 的图象,由图可知,要使方程f (x )-ax =0有5个不同实根,即y =f (x )和y =ax 的图象有5个交点.由图可知,当x ∈(3,5)时,f (x )=-(x -4)2+1,此时若y =ax 与其相切,则a =8-215;又方程f (x )=ax 在(5,6)无解,得a >16,故正实数a 的取值范围是(16,8-215),选D. 6.已知f (x )是定义在R 上且以2为周期的偶函数,当0≤x ≤1时,f (x )=x 2.如果函数g (x )=f (x )-(x +m )有两个零点,则实数m 的值为( )A .2k (k ∈Z)B .2k 或2k +14(k ∈Z)C .0D .2k 或2k -14(k ∈Z)【答案】D7.某企业投入100万元购入一套设备,该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.为使该设备年平均费用最低,该企业________年后需要更新设备. 【答案】10【解析】由题意可知x 年的维护费用为2+4+…+2x =x (x +1),所以x 年的平均费用y =100+0.5x +x x +x=x +100x +1.5,由基本不等式得y =x +100x+1.5≥2x ·100x+1.5=21.5,当且仅当x =100x,即x =10时取等号,所以该企业10年后需要更新设备.8.我们把形如y =b|x |-a (a >0,b >0)的函数因其图象类似于汉字中的“囧”字,故生动地称为“囧函数”,若当a =1,b =1时的“囧函数”与函数y =lg|x |的交点个数为n ,则n =________. 【答案】 4【解析】由题意知,当a =1,b =1时,y =1|x |-1=⎩⎪⎨⎪⎧1x -1x ≥0且x ,-1x +1x <0且x ≠-在同一坐标系中画出“囧函数”与函数y =lg|x |的图象如图所示,易知它们有4个交点.9.若函数f (x )=⎩⎪⎨⎪⎧2x-a ,x ≤0,ln x ,x >0有两个不同的零点,则实数a 的取值范围是________.【答案】 (0,1]10.已知函数f (x )=1x +2-m |x |有三个零点,则实数m 的取值范围为________. 【答案】m >1【解析】函数f (x )有三个零点等价于方程1x +2=m |x |有且仅有三个实根. ∵1x +2=m |x |⇔1m =|x |(x +2),作函数y =|x |(x +2)的图象,如图所示,由图象可知m 应满足0<1m<1,故m >1.11.已知函数f (x )=⎩⎪⎨⎪⎧x +1,x ≤0,log 2x ,x >0,则函数y =f [f (x )+1]的零点有________个.【答案】4【解析】当f (x )=0时,x =-1或x =1,故f [f (x )+1]=0时,f (x )+1=-1或1.当f (x )+1=-1,即f (x )=-2时,解得x =-3或x =14;当f (x )+1=1,即f (x )=0时,解得x =-1或x =1.故函数y =f [f (x )+1]有4个不同的零点.12.已知函数f (x )=|ln x |,g (x )=⎩⎪⎨⎪⎧0,0<x ≤1,|x 2-4|-2,x >1,则方程|f (x )+g (x )|=1实根的个数为________.【答案】413.已知函数f (x )=⎩⎪⎨⎪⎧2x-1,x >0,-x 2-2x ,x ≤0,若函数g (x )=f (x )-m 有3个零点,则实数m 的取值范围是________.【答案】(0,1)【解析】画出f (x )=⎩⎪⎨⎪⎧2x-1,x >0,-x 2-2x ,x ≤0的图象,如图.由于函数g (x )=f (x )-m 有3个零点, 结合图象得:0<m <1, 即m ∈(0,1).14.已知函数f (x )=5x+x -2,g (x )=log 5x +x -2的零点分别为x 1,x 2,则x 1+x 2的值为________. 【答案】215.在如图所示的锐角三角形空地中,欲建一个面积最大的内接矩形花园(阴影部分),则其边长x 为________m.【答案】 20 【解析】如图,过A 作AH ⊥BC 交于点H ,交DE 于点F ,易知DE BC =x 40=AD AB =AF AH ⇒AF =x ⇒FH =40-x ,则S =x (40-x )≤(402)2,当且仅当40-x =x ,即x =20时取等号,所以满足题意的边长x 为20m.16.已知函数f (x )=mx 2-2x +1有且仅有一个正实数的零点,求实数m 的取值范围.17.随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员2a 人(140<2a <420,且a 为偶数),每人每年可创利b 万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b 万元,但公司需付下岗职员每人每年0.4b 万元的生活费,并且该公司正常运转所需人数不得小于现有职员的34,为获得最大的经济效益,该公司应裁员多少人?【解析】解 设裁员x 人,可获得的经济效益为y 万元,则y =(2a -x )(b +0.01bx )-0.4bx=-b100[x 2-2(a -70)x ]+2ab .依题意得2a -x ≥34·2a ,所以0<x ≤a2.又140<2a <420,即70<a <210.①当0<a -70≤a2,即70<a ≤140时,x =a -70,y 取到最大值;②当a -70>a 2,即140<a <210时,x =a2,y 取到最大值.故当70<a <140时,公司应裁员(a -70)人,经济效益取到最大; 当140<a <210时,公司应裁员a2人,经济效益取到最大.。
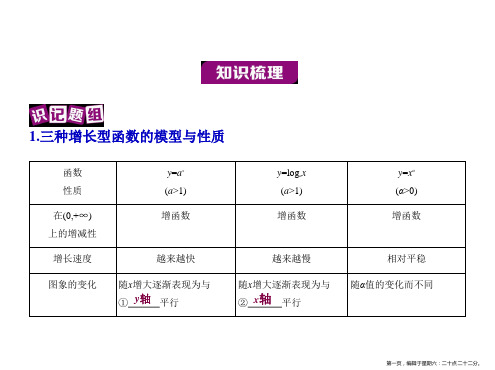


§2.6函数模型及其应用
重难点:将实际问题转化为函数模型,比较常数函数、一次函数、指数函数、对数函数模型的增长差异,结合实例体会直线上升、指数爆炸、对数增长等不同类型的函数增长的含义.
考纲要求:①了解指数函数、对数函数以及幂函数的增长特征,知道直线上升、指数增长、对数增长等不同
函数类型增长的含义;
②了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.
经典例题:1995年我国人口总数是12亿.如果人口的自然年增长率控制在1.25%,问哪一年我国人口总数将超过14亿.
当堂练习:
1.某物体一天中的温度T 是时间t 的函数: T(t)=t 3
-3t+60,时间单位是小时,温度单位是C ︒,当t=0表示中
午12:00,其后t 值取为正,则上午8时的温度是( )
A .8 C ︒
B .112
C ︒ C .58 C ︒
D .18C ︒
2.某商店卖A 、B 两种价格不同的商品,由于商品A 连续两次提价20%,同时商品B 连续两次降价20%,结果都以每件2
3.04元售出,若商店同时售出这两种商品各一件,则与价格不升、不降的情况相比较,商店盈利的情况是:( )
A .多赚5.92元
B .少赚5.92元
C .多赚28.92元
D .盈利相同
3.某厂生产中所需一些配件可以外购,也可以自己生产,如外购,每个价格是1.10元;如果自己生产,则每月的固定成本将增加800元,并且生产每个配件的材料和劳力需0.60元,则决定此配件外购或自产的转折点是( )件(即生产多少件以上自产合算)
A .1000
B .1200
C .1400
D .1600 4
则x,y 的函数关系与下列哪类函数最接近?(其中a,b 为待定系数) ( )
A .y=a+b X
B .y=a+bx
C .y=a+log b x
D .y=a+b/x
5.某产品的总成本y (万元)与产量x (台)之间的函数关系式是y =3000+20x -0.1x 2
(0<x <240,x ∈N ),若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量是( ) A .100台
B .120台
C .150台
D .180台
6.购买手机的“全球通”卡,使用须付“基本月租费”(每月需交的固定费用)50元,在市内通话时每分钟另收话费0.40元;购买“神州行”卡,使用时不收“基本月租费”,但在市内通话时每分钟话费为0.60元.若某用户每月手机费预算为120元,则它购买_________卡才合算.
7.某商场购进一批单价为6元的日用品,销售一段时间后,为了获得更多利润,商场决定提高销售价格。
经试验发现,若按每件20元的价格销售时,每月能卖360件,若按25元的价格销售时,每月能卖210件,假定每月销售件数y (件)是价格x (元/件)的一次函数。
试求y 与x 之间的关系式 . 在商品不积压,且不考虑其它因素的条件下,问销售价格定为 时,才能时每月获得最大利润. 每月的最大利润是 .
8.某企业生产的新产品必须先靠广告来打开销路.该产品的广告效应应该是产品的销售额与广告费之间的差.如果销售额与广告费的算术平方根成正比,根据对市场进行抽样调查显示:每付出100元的广告费,所得的销售额是1000元.问该企业应该投入 广告费,才能获得最大的广告效应.
9.商店出售茶壶和茶杯,茶壶每只定价为20元,茶杯每只定价5元,该店制定了两种优惠办法:(1)买一只茶壶送一只茶杯;(2)按总价的92%付款;某顾客需购茶壶4只,茶杯若干只(不少于4只).则当购买茶杯数 时, 按(2)方法更省钱.
10.一块形状为直角三角形的铁皮,直角边长分别为40cm 和60cm,现要将它剪成一个矩形,并以此三角形的直角为矩形的一个角,则矩形的最大面积是 .
11.某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y 与时间t 之间近似满足如图所示的曲线.
(1)写出服药后y 与t 之间的函数关系式;
(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假若某病人一天中第一次服药时间为上午7:00,问一天中怎样安排服药的时间(共4次)效果最佳.
12.某省两个相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为公共交通车,已知如果该列火车每次拖4节车厢,能来回16次;如果每次拖7节车厢,则能来回10次.每日来回次数是每次拖挂车厢个数的一次函数,每节车厢一次能载客110人,问:这列火车每天来回多少次,每次应拖挂多少节车厢才能使营运人数最多?并求出每天最多的营运人数.
13.市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析,发现有如下规律:该商品的价格每上涨 x %(x >0),销售数量就减少kx % (其中k 为正常数).目前,该商品定价为a 元, 统计其销售数量为b 个. (1)当k =
12
时,该商品的价格上涨多少,就能使销售的总金额达到最大.
(2)在适当的涨价过程中,求使销售总金额不断增加时k 的取值范围.
14.某工厂今年1月、2月、3月生产某种产品的数量分别为l 万件,1.2万件,1.3万件.为了估测以后每个月的产量,以这三个月的产品数量为依据.用一个函数模拟该产品的月产量y 与月份x 的关系,模拟函数可以选用二次函数或函数x
y ab c =+ (其中a ,b ,c 为常数).已知4月份该产品的产量为1.37万件,请问用以上哪个函数作为模拟函数较好.并说明理由.
§2.6函数模型及其应用
经典例题:解:设x 年后我国人口总数为y ,则有y =12·(1+0.0125)x
,依题意,得y >14, 即12·(1+0.0125)x
>14,即(1+0.0125)x
>
1412
.
两边取对数,得x lg1.0125>lg14-lg12.所以x >
lg14lg12lg1.125
-≈12.4.
答:13年后,即2008年我国人口总数将超过14亿. 当堂练习:
1.A ;
2. C ;
3. D ;
4. A ;
5. C ;
6. 神州行;
7. y= -10x+560,31, 6250;
8. 2500;
9. 大于34; 10. 6002
cm ;
11. (1)依题得,601220
11033
t
t y t t ≤≤=-+<≤⎧⎪
⎨⎪⎩ (2)设第二次服药时在第一次服药后t 1小时,则4413
20
1
32=⇒=+-t t ,因而第二次服药应在11:00; 设第
三次服药在第一次服药后t 2小时,则此时血液中含药量应为两次服药量的和,即有
,4)4(320232320232=+--+-t t 解得t 2=9小时,故第三次服药应在16:00;设第四次服药在第一次后t 3小时(t 3>10),则此时第一次服进的药已吸收完,此时血液中含药量应为第二、三次的和,
,4)9()4(3
20232320232=+--+--t t 解得t 3=13.5小时,故第四次服药应在20:30. 12.设每日来回y 次,每次挂x 节车厢,由题意,y =kx +b ,且当x =4时,y =16;当x =7时,y =10.解得:k =-2,
b =24,∴y =-2x +24. 由题意,每次挂车厢最多时,营运人数最多,设每日拖挂W 节车厢,则W =2xy =2x (-
2x +24)=-4x 2
+48x =-4(x -6)2
+144,
∴当x =6时,W max =144,此时,y =12,最多营运15840人.
13.解:依题意,价格上涨x %后,销售总金额为: y =a (1+x %)· b (1-kx %)=10000
ab [-kx 2
+100(1-k )x +10000].
(1)取k =12
,y =
10000
ab [-
12
x 2+50x +10000],∴x = 50, 即商品价格上涨50%时, y 最大为
9
8ab .
(2)因为y =
10000
ab
[-kx 2
+100(1-k )x +10000],此二次函数开口向下,对称轴为x =
50(1)
k k
-,在适
当涨价过程中,销售总金额不断增加,即要求此函数当自变量x 在{x |x >0}的一个子集中增大时,y 也增大.所以
50(1)
k k
->0,解之0<k <1.
14.设二次函数为y=px 2
+qx+r ,则10.05
42 1.20.3593 1.30.7p q r p p q r q p q r r ++==-++=⇒=++==⎧⎧⎪⎪
⎨⎨⎪⎪⎩⎩
,
所以2
0.050.350.7y x x =-++,当x=4时, y=1.3;
对于函数x
y ab c =+,由2310.8
1.20.51.4
1.3ab c a ab c b c ab c +==-+=⇒==+=⎧⎧⎪⎪⎨⎨⎪⎪⎩⎩
,所以10.8() 1.42x y =-⋅+,当
x=4时, y=1.35,显
然,用函数1
0.8() 1.42
x
y =-⋅+作为模拟函数较好.。