弹塑性力学基本理论及应用__第八章_能量原理及其应用
- 格式:doc
- 大小:903.00 KB
- 文档页数:30

弹塑性力学简答题第一章 应力1、 什么是偏应力状态?什么是静水压力状态?举例说明?静水压力状态时指微六面体的每个面只有正应力作用,偏应力状态是从应力状态中扣除静水压力后剩下的部分。
2、应力边界条件所描述的物理本质是什么?物体边界点的平衡条件。
3、对照应力张量ij δ与偏应力张量ij S ,试问:两者之间的关系?两者主方向之间的关系?相同。
110220330S S S σσσσσσ=+=+=+。
4、为什么定义物体内部应力状态的时候要采取在一点的领域取极限的方法?不规则,内部受力不一样。
5、解释应力空间中为什么应力状态不能位于加载面之外?保证位移单值连续。
连续体的形变分量x ε、y ε、xy τ不是互相独立的,而是相关,否则导致位移不单值,不连续。
6、Pie 平面上的点所代表的应力状态有何特点?该平面上任意一点的所代表值的应力状态1+2+3=0,为偏应力状态,且该平面上任一法线所代表的应力状态其应力解不唯一。
固体力学解答必须满足的三个条件是什么?可否忽略其中一个?第二章 应变1、从数学和物理的不同角度,阐述相容方程的意义。
从数学角度看,由于几何方程是6个,而待求的位移分量是3个,方程数目多于未知函数的数目,求解出的位移不单值。
从物理角度看,物体各点可以想象成微小六面体,微单元体之间就会出现“裂缝”或者相互“嵌入”,即产生不连续。
2、两个材料不同、但几何形状、边界条件及体积力(且体积力为常数)等都完全相同的线弹性平面问题,它们的应力分布是否相同?为什么?相同。
应力分布受到平衡方程、变形协调方程及力边界条件,未涉及本构方程,与材料性质无关。
3、应力状态是否可以位于加载面外?为什么?不可以。
保证位移单值连续。
连续体的形变分量x ε、y ε、xy τ不是互相独立的,而是相关,否则导致位移不单值,不连续。
4、给定单值连续的位移函数,通过几何方程可求出应变分量,问这些应变分量是否满足变形协调方程?为什么?满足。


弹塑性力学理论及其在工程上的应用欧阳家百(2021.03.07)摘要:弹塑性力学理论在工程中应用十分的广泛,是工程中分析问题的一个重要手段,本文首先是对弹塑性力学理论进行了阐述,然后讨论了它在工程上面的应用。
关键词:弹塑性力学;工程;应用第一章弹塑性力学的基本理论(一)应力理论1、应力和应力张量在外力作用下,物体将产生应力和变形,即物体中诸元素之间的相对位置发生变化,由于这种变化,便产生了企图恢复其初始状态的附加相互作用力。
用以描述物体在受力后任何部位的内力和变形的力学量是应力和应变。
本章将讨论应力矢量和某一点处的应力状态。
为了说明应力的概念,假想把受—组平衡力系作用的物体用一平面A分成A和B两部分(图1.1)。
如将B部分移去,则B对A的作用应代之以B部分对A部分的作用力。
这种力在B移去以前是物体内A与B 之间在截面C 的内力,且为分布力。
如从C 面上点P 处取出一包括P 点在内的微小面积元素S ∆,而S ∆上的内力矢量为F ∆,则内力的平均集度为F ∆/S ∆,如令S ∆无限缩小而趋于点P ,则在内力连续分布的条件下F ∆/S ∆趋于一定的极限σo ,即2、二维应力状态与平面问题的平衡微分方程式上节中讨论应力概念时,是从三维受力物体出发的,其中点P 是从一个三维空间中取出来约点。
为简单起见,首先讨论平面问题。
掌提了平面问题以后.再讨论空间问题就比较容易了。
当受载物体所受的面力和体力以及其应力都与某—个坐标轴(例如z 轴)无关。
平面问题又分为平面应力问题与平面应变问题。
(1) 平面应力问题如果考虑如图所示物体是一个很薄的平板,荷载只作用在板边,且平行于板面,即xy 平面,z 方向的体力分量Z 及面力分量z F 均为零,则板面上(2/δ±=z 处)应力分量为图2.2平面应力问题因板的厚度很小,外荷载又沿厚度均匀分布,所以可以近似地认为应力沿厚度均匀分布。
由此,在垂直于z 轴的任一微小面积上均有0=z σ, 0==zy zx ττ根据切应力互等定理,即应力张量的对称性,必然有0==xz yx ττ。

弹塑性力学基础理论与应用弹塑性力学是力学中一个重要的分支,涵盖了弹性力学和塑性力学的基本原理和应用。
本文将简要介绍弹塑性力学的基础理论和一些应用领域。
一、弹塑性力学的基础理论1. 弹性力学理论弹性力学研究材料在外力作用下的弹性变形及其恢复过程。
根据胡克定律,应力与应变成正比。
弹性力学理论通过应力张量与应变张量之间的关系描述了弹性材料的力学行为。
弹性模量是弹性力学的重要参数,表征了材料的刚度。
2. 塑性力学理论塑性力学研究材料在超过弹性极限后的变形行为。
当外力超过材料的弹性极限时,材料会发生塑性变形,而不是立即恢复到原来的形状。
塑性力学理论包括弹塑性本构方程的建立和塑性流动规律的描述。
3. 弹塑性力学理论弹塑性力学是弹性力学和塑性力学的综合应用。
它考虑了材料在弹性和塑性行为之间的转换。
在某些情况下,材料可以同时表现出弹性和塑性特性。
弹塑性力学理论利用不同的本构关系来描述材料在变形过程中的不同阶段。
二、弹塑性力学的应用1. 材料工程弹塑性力学在材料工程领域中具有重要的应用价值。
通过研究材料的弹性行为和塑性行为,可以确定材料的强度、韧性和耐久性,从而指导材料的选用和设计。
在材料的加工过程中,弹塑性力学理论也可以用于模拟和预测材料的变形行为。
2. 结构工程在结构设计和分析中,弹塑性力学也发挥着重要作用。
结构的承载能力和变形行为与材料的弹性和塑性特性密切相关。
通过考虑弹塑性行为,可以更准确地评估结构的安全性和稳定性。
3. 土木工程土木工程中的地基和土壤材料往往存在复杂的弹塑性特性。
弹塑性力学可用于分析土壤的沉降和变形行为,以及地基的稳定性。
在岩土工程中,弹塑性力学理论也可以用于分析岩土体的稳定性和变形行为。
4. 金属加工金属的塑性变形是金属加工过程中的核心问题。
弹塑性力学理论可以用于研究金属的屈服和流动行为,从而指导金属的模具设计和加工工艺的优化。
总结:弹塑性力学是力学中的一个重要分支,它综合了弹性力学和塑性力学的基础理论与应用。

弹性与塑性力学的实际应用弹性力学和塑性力学是材料力学中重要的分支,它们研究材料在受力后的变形行为以及力学性能。
这两个领域的实际应用广泛,涉及到许多重要的行业和领域,如建筑工程、航空航天、汽车制造等。
本文将探讨弹性与塑性力学在实际应用中的重要性和具体例子。
一、桥梁工程弹性力学在桥梁工程中具有重要的应用。
桥梁是连接两个地点的重要交通枢纽,承受着巨大的力和重压。
桥梁的设计和施工必须考虑到材料的弹性变形和应力分布情况。
桥梁结构需要能够在受力后恢复原状,以满足不同条件下的荷载要求。
弹性力学的理论和实践指导了桥梁设计的合理性和稳定性。
然而,桥梁在长期使用过程中也面临着塑性变形的问题。
例如,大型桥梁和高速桥梁常常会受到车辆行驶引起的动力荷载和温度的影响,从而导致塑性变形和局部破坏。
为了保证桥梁的可靠性和持久性,塑性力学的知识和方法在桥梁维护和检修中应用广泛。
通过对桥梁的结构和材料进行分析和评估,可以及时采取措施来防止塑性变形和延长桥梁的使用寿命。
二、航空航天工程在航空航天工程中,弹性与塑性力学的应用尤为重要。
飞机、航天器等航空器件需要在极端的条件下工作,如高速飞行、大气压力和温度变化等。
因此,航空材料必须具备良好的弹性和塑性特性,以确保飞行器的安全和性能。
弹性力学的理论被广泛用于航空器的设计和性能评估。
通过对材料的弹性恢复和应力分析,可以保证飞机和航天器在受力后不会发生永久塑性变形,并且能够承受外界环境的冲击和压力。
同时,塑性力学的知识也被应用于航天器的失效分析和事故调查中,以确定外界因素和材料的塑性行为对飞行器引起的损伤和事故的影响。
三、汽车制造弹性与塑性力学在汽车制造中具有广泛的实际应用。
汽车是人们日常生活中不可或缺的交通工具,对于汽车的安全性、舒适性和经济性要求越来越高。
因此,汽车制造必须考虑到材料的弹性和塑性特性,以提高车辆的整体性能和使用寿命。
弹性力学的理论被广泛用于汽车零部件的设计和制造中。
例如,发动机的缸体、活塞和连杆等构件必须具备良好的弹性特性,以承受高压力和高温环境下的工作要求,同时尽量减少能量损耗和振动噪声。

弹塑性力学课程介绍
课程编号:08070603 课程类别:学科基础课
课程名称:弹塑性力学英译名称:elastic-plastic mechanics
学时:40 学分:2
开课学期:1 教学方式:讲授+讨论
考核方式:开卷考试适用学科:化工过程机械
授课单位及教师梯队:机电学院教师
内容简介:
主要讲授弹性力学和塑性力学的基本概念、理论和方法,以及各种经典方法在解决弹塑性问题中的应用。
本课程主要包括:绪论和张量介绍,应力应变分析,屈服条件和本构关系,弹塑性问题的提法,弹塑性平面问题,薄板的弯曲,薄壳的基本理论,理想刚塑性平面应变问题,柱体的弹塑性扭转,能量原理,塑性极限分析等内容。
参考书目:
1. 《弹性力学》徐芝伦,高教出版社
2. 《弹塑性力学引论》杨桂通,清华大学出版社
3. 《工程弹塑性力学》孙炳楠等,浙大出版社
4. 《应用弹塑性力学》徐秉业等,清华出版社。



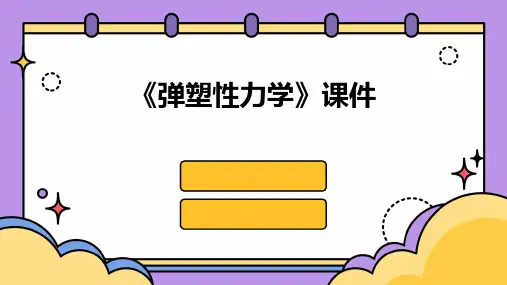

弹塑性⼒学定理和公式应⼒应变关系弹性模量||⼴义虎克定律1.弹性模量对于应⼒分量与应变分量成线性关系的各向同性弹性体,常⽤的弹性常数包括:a弹性模量单向拉伸或压缩时正应⼒与线应变之⽐,即b切变模量切应⼒与相应的切应变之⽐,即c体积弹性模量三向平均应⼒与体积应变θ(=εx+εy+εz)之⽐,即d泊松⽐单向正应⼒引起的横向线应变ε1的绝对值与轴向线应变ε的绝对值之⽐,即此外还有拉梅常数λ。
对于各向同性材料,这五个常数中只有两个是独⽴的。
常⽤弹性常数之间的关系见表3-1 弹性常数间的关系。
室温下弹性常数的典型值见表3-2 弹性常数的典型值。
2.⼴义虎克定律线弹性材料在复杂应⼒状态下的应⼒应变关系称为⼴义虎克定律。
它是由实验确定,通常称为物性⽅程,反映弹性体变形的物理本质。
A各向同性材料的⼴义虎克定律表达式(见表3-3 ⼴义胡克定律表达式)对于圆柱坐标和球坐标,表中三向应⼒公式中的x 、y、z分别⽤r、θ、z和r、θ、φ代替。
对于平⾯极坐标,表中平⾯应⼒和平⾯应变公式中的x、y、z⽤r、θ、z代替。
B⽤偏量形式和体积弹性定律表⽰的⼴义虎克定律应⼒和应变量分解为球量和偏量两部分时,虎克定律可写成更简单的形式,即体积弹性定律应⼒偏量与应变偏量关系式在直⾓坐标中,i,j=x,y,z;在圆柱坐标中,i,j=r,θ,z,在球坐标中i,j=r,θ,φ。
弹性⼒学基本⽅程及其解法弹性⼒学基本⽅程|| 边界条件|| 按位移求解的弹性⼒学基本⽅法|| 按应⼒求解的弹性⼒学基本⽅程|| 平⾯问题的基本⽅程|| 基本⽅程的解法|| ⼆维和三维问题常⽤的应⼒、位移公式1.弹性⼒学基本⽅程在弹性⼒学⼀般问题中,需要确定15个未知量,即6个应⼒分量,6个应变分量和3个位移分量。
这15个未知量可由15个线性⽅程确定,即(1)3个平衡⽅程[式(2-1-22)],或⽤脚标形式简写为(2)6个变形⼏何⽅程[式(2-1-29)],或简写为(3)6个物性⽅程[式(3-5)或式(3-6)],简写为或2.边界条件弹性⼒学⼀般问题的解,在物体部满⾜上述线性⽅程组,在边界上必须满⾜给定的边界条件。
弹塑性力学在桥梁中的应用与研究桥梁作为重要的交通基础设施,其安全性和可靠性对经济发展和人民生活具有重要意义。
在桥梁设计和施工过程中,弹塑性力学是最为关键的理论基础之一。
本文将介绍弹塑性力学在桥梁中的应用背景和研究意义,并综述其在桥梁中的应用现状、发展趋势及研究方法。
弹塑性力学是研究材料在应力超过弹性极限后变形和行为的理论。
在桥梁领域,弹塑性力学广泛应用于结构分析、地震响应分析、疲劳损伤分析等方面。
近年来,随着计算机技术的快速发展,数值模拟方法在桥梁工程中越来越受到重视。
通过有限元方法、边界元方法、粒子群算法等数值模拟方法,可以更准确地模拟桥梁在复杂荷载作用下的行为。
在桥梁结构分析中,弹塑性力学可用于研究桥梁在承载过程中的变形、内力分布和承载能力。
例如,通过有限元方法,可以模拟桥梁在车辆荷载、自重等作用下的变形和内力分布,为桥梁设计提供依据。
地震响应分析是确保桥梁安全性的重要环节。
弹塑性力学可以模拟桥梁在地震作用下的变形、位移和内力变化情况,为采取有效的抗震措施提供理论支持。
疲劳损伤是影响桥梁寿命的主要因素之一。
通过弹塑性力学,可以模拟桥梁在车辆荷载、风荷载等循环荷载作用下的疲劳损伤过程,为采取有效的疲劳损伤控制措施提供依据。
有限元方法是一种常用的数值模拟方法,通过将结构离散化为有限个单元,对每个单元进行受力分析,进而得到整个结构的受力状态。
有限元方法在桥梁弹塑性分析中具有广泛应用。
边界元方法是一种用于解决边界值问题的数值模拟方法。
在桥梁弹塑性分析中,边界元方法可以用于解决桥梁表面应力分布等问题。
粒子群算法是一种智能优化算法,通过模拟鸟群、鱼群等动物群体的行为,寻找问题的最优解。
在桥梁弹塑性分析中,粒子群算法可以用于优化桥梁的结构设计,提高其承载能力和稳定性。
弹塑性力学在桥梁中的应用已经取得了许多重要的成果。
例如,通过弹塑性力学分析,成功地预测了某高速公路大桥在车辆荷载作用下的变形和内力分布,为该桥的设计提供了重要依据。
《弹塑性力学》课程第一篇 基础理论部分第一章 应力状态理论1.1 基本概念1. 应力的概念应力:微分面上内力的分布集度。
从数学上看,应力sPF s ∆∆=→∆0lim ν由于微分面上的应力是一个矢量,因此,它可以分解成微分面法线方向的正应力νσ和微分面上的剪应力ντ。
注意弹塑性力学中正应力和剪应力的正负号规定。
2. 一点的应力状态(1)一点的应力状态概念凡提到应力,必须同时指明它是对物体内哪一点并过该点的哪一个微分面。
物体内同一点各微分面上的应力情况,称为该点的应力状态。
(2)应力张量物体内任一点不同微分面上的应力情况一般是不同的,这就产生了一个如何描绘一点的应力状态的问题。
应力张量概念的提出,就是为了解决这个问题。
在直角坐标系里,一点的应力张量可表示为⎪⎪⎪⎪⎭⎫⎝⎛=z zy zx yz yyx xz xy x ij στττστττσσ若已知一点的应力张量,则过该点任意微分面ν上的应力矢量p就可以由以下公式求出:n m l p xz xy x x ττσν++= (1-1’a ) n m l p yz y yx y τστν++=(1-1’b )n m l p z zy zx z σττν++=(1-1’c )由式(1-1),还可进一步求出该微分面上的总应力p 、正应力νσ和剪应力v τ: 222z y x p p p p ++=(1-2a )nl mn lm n m l zx yz xy z y x τττσσσσν222222+++++=(1-2b )22ννστ-=p(1-2c )(3)主平面、主方向与主应力由一点的应力状态概念可知,通过物体内任一点都可能存在这样的微分面:在该微分面上,只有正应力,而剪应力为零。
这样的微分面即称为主平面,该面的法线方向即称为主方向,相应的正应力称为主应力。
主应力、主方向的求解在数学上归结为求解以下的特征问题:}{}]{[i n i ij n n σσ=(1-3)式中,][ij σ为该点应力张量分量构成的矩阵,n σ为主应力,}{i n 为主方向矢量。
第八章 能量原理及其应用弹塑性力学问题实质上是边值问题,即求解满足一定边界条件的偏微分方程组。
然而只有对一些特殊的结构在特定加载条件下才能找到精确解,而对于一般的力学问题,如空间问题,泛定方程为含有15个未知量的6个偏微分方程,在给定边界条件时.求解是极其困难的,而且往往足小对能的。
因此,为了解决具体的工程结构力学问题,目前都广泛应用数值方法,如有限元法、无限元法、边界元法、无网格化法及样条元法等等。
这些解法的依据都是能量原理。
本章将讨论利用能量原理和极值原理求解弹塑性力学问题的近似解法。
本章共讨论五个能量原理。
首先是虚位移原理,由虚位移原理推导出最小势能原理,其次介绍虚应力原理,和由虚应力原理推导出最小余能原理。
另外,还简单介绍最大耗散能原理。
本章还讲述了根据上述的能量原理建立的有关弹性力学问题的数值解法。
8.1 基本概念1.1 物体变形的热力学过程由第四章知,物体在外界因素影响下的变形过程,严格来说都是一个热力学过程。
因此研究物体的状态,不仅要知道物体的变形状态,而且还要知道物体中每一点的温度。
如果物体在变形过程中,各点的温度与其周围介质的温度保持平衡,则称这一过程为等温过程;若在变形过程中,物体的温度没有改变,即既没有热量损失也没有热量增加,则称这一过程为绝热过程。
物体的瞬态高频振动,高速变形过程都可视为绝热过程。
令物体在变形过程中的动能为E ,应变能为U ,则在微小的t δ时间间隔内,物体从一种状态过渡到另一种状态时,根据热力学第一定律,总能量的变化为 Q W U E δδδδ+=+ (a) 其中,W δ为作用于物体上的体力和面力所完成的功;Q δ是物体由其周围介质所吸收(或向外发散)的热量,并以等量的功度量。
假定弹性变形过程是绝热的,则对于静力平衡问题有00==Q ,E δδ (b)将式(b)代入式(a),则有W U δδ= (8.1-1)1.2 应变能由第四章的式(4.1-5b)知,在线弹性情况下,单位体积的应变能为ik ij ij ij ij d U εσεσε2100==⎰ (8.1-2)对于一维应力状态,在x x εσ-平面内,则0U 实际上就是应力应变曲线与x ε轴和'x x εε=所围成的面积(图8.1),即⎰='0Xx x d U εεσ (8.1-3)其中'x ε是物体变形过程某一指定时刻的应变,应 图8.1 应变能与应变余能 变能0U 表示物体在变形过程中所储存的能量。
1.3 应变余能在图8.1中, 如果令'0U 表示应力应变曲线与x σ轴和'x x σσ=所围成的面积,即⎰=''xx x d U σσε (8.1-4)式中'x σ是物体变形过程某一指定时刻的应力。
称'0U 为单位体积的应变余能,简称余能,有时又称其为应力能。
由于'x σ和'x ε是物体变形过程中同一时刻的应力和应变,因此有'00''U U x x +=εσ由此可见,0U 与'0U 互补或互余对方为''x x εσ矩形的面积。
显然,在线弹性情况下有'00U U =,即余能与应变能在数值上相等。
尽管应变余能不像应变能那样具有明确的物理意义,但引入应变余能这一概念后,使讨论问题的范围扩大了。
8.2 虚位移原理与最小势能原理2.1 虚位移原理设有变形体在外力作用下处于平衡状态。
此处,外为包括体力分量X ,Y ,Z 及一部分表面的面力分量X ,Y ,Z 。
假如有一组位移分量u ,v ,w 既能满足用位移表示的平衡方程,又能满足位移边界条件以及用位移分量表示的应力边界条件。
现在设想在变形体几何约束所允许的条件下,给它一个任意的微小变化,即所谓虚位移或位移变分u δ,v δ,w δ,得到一组新的位移 w w w v v v u u u δδδ+=+=+=''',,(a)下面考察能量发生了什么变化。
这时,外力在虚位移上所做的功(称为虚功)为dS w Z v Y u X dV w Z v Y u X W S V⎰⎰⎰⎰⎰+++++=σδδδδδδδ)()( (8.2-1a)或dS u F dV u f W i S i i Vi δδδσ⎰⎰⎰⎰⎰+= (8.2-1b)式中,V 为变形体的全部体积,S 为变形体的全部表面积,其中给定外力的表面记为σS ,给定位移的表面记为露u S 。
但面积分仅对给定面力的那一部分表面进行,对于给定位移的那一部分表面,因无虚位移,故不必考虑。
应该指出,这里所说的虚位移—般并不是由实际外力所引起的,而是由其他因素所引起,或者是为了分析问题而假想的。
虚位移发生时,约束反力是不作功的,这是因为在约束力方向不可能产生位移。
物体产生虚位移的过程中,物体必然产生微小的虚变形,因此在变形体中就产生虚应变能,即⎰⎰⎰+++++=Vzx zx yz yz xy xy z z y y x x dV U )(δγτδγτδγτδεσδεσδεσδ (8.2-2a)或写为⎰⎰⎰=Vij ij dV U δεσδ (8.2-2b)假定变形体在虚位移的过程中,并没有温度和速度的改变,因而也就没有热能和动能的改变。
则按照能量守恒定律或热力学第一定律,应变能在虚位移上的增量U δ,应当等于外力在虚位移所做的虚功,于是有⎰⎰⎰+++++Vzx zx yz yz xy xy z z y y x xdV )(δγτδγτδγτδεσδεσδεσdS w Z v Y u X dV w Z v Y u X S V⎰⎰⎰⎰⎰+++++=σδδδδδδ)()( (8.2-3)式(8.2-3)即为虚位移原理的位移变分方程,也称为拉格朗日(Lagrange)变分方程,有时也称为虚功方程。
因此,虚位移原理可叙述为:在外力作用下处于平衡状态的可变形体,当给予物体微小虚位移时,外力在虚位移上所做虚功等于物体的虚应变能。
现详细证明如下:若在虚位移原理的变分方程(8.2-3)中,因给定位移的部分表面u S 上0=i u δ,而在给定面力的部分表面σS 上,边界条件i j ij F n =σ成立。
则式(8.2-3)中右边对σS 的积分可以写为对整个物体表面S 的积分,即有⎰⎰⎰⎰+=+=Si j ij i Vi i S i i Vi dS u n dV u f dS u F dV u f W δσδδδδσ(8.2-4)运用高斯散度定理,将上式对体积积分化为面积分,有dS wn vm ul dV z w y v x u S z y x V z y x ⎰⎰⎰⎰⎰++=⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂)()()()(δσδσδσδσδσδσ (8.2-5) 其中n m l ,,为外边界法线方向单位矢量n的方向余弦,即,cos(x l =n), ,cos(y m =n), ,cos(z n =n)注意到⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰=⎥⎦⎤⎢⎣⎡∂∂+∂∂=⎥⎦⎤⎢⎣⎡∂∂S x V x V V x x udS l dV x u udV x dV x u δσδσδσδσ)()( 以及⎰⎰⎰⎰⎰⎰⎰⎰+=⎥⎦⎤⎢⎣⎡∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂+∂∂S xy V xy xy V xy dS u m v l dV u y v x dV u y v x )(δδτδτδτδδτ 其余的类似,因此由以上两式可得⎰⎰=Si j ij j Vi ij dS u n dV u δσδσ,)( (8.2-6)式中n m l n j ,,=。
将式(8.2-6)代入式(8.2-4),有⎰⎰⎰⎰⎰⎰++=++=+=Vj i ij i Vi j ij Vj i ij i j ij i V i j Vi ij i Vi dVu dV u f dV u u dV u f dVu dV u f W ,),(),,(,)(δσδσδσδσδδσδδ (b)当物体处于平衡状态时,因为0,=+i j ij f σ所以式(b)中笫一项积分为零。
又因),,(21,i j j i ij ji ij u u δδδεσσ+==所以有ij ij j i ij u δεσδσ=,于是由式(b)得⎰=Vij ij dV W δεσδ将上式与式(8.2-2b)比较可知,有U W δδ=以上证明说明,当给予系统微小虚位移时,外力所作虚功与物体的虚应变能相等是物体处于平衡状态的必要条件。
另外,由应变位移关系以及先变分后微分与先微分后变分等价可知⎪⎪⎭⎪⎪⎬⎫∂∂+∂∂=∂∂+∂∂=∂∂=∂∂=ΛΛ),()()(),(u y v x x v y u u x x u xyx δδδδγδδδε (c) 将式(c)代入(8.2-2a),经分部积分和利用格林公式,可得到如同下列形式的三个关系式⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∂∂-=∂∂-∂∂=∂∂=V xS x V x x V V xVx x udVxudS l dV xu dV u x dV u x dV δσδσσδδσδσδεσ)()()( (d)以及下列形式的三个关系式dVu y v x dS u m v l dV u y v x dV V xyxy S xy V V xy xy xy ⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∂∂+∂∂-+=⎥⎦⎤⎢⎣⎡∂∂+∂∂=)()()()()(δτδτδδτδδτδγτ (e)将式(d)、(e) 所表示构六个关系式代人(8.2-2)式,则得[]dVw z y x vzy x u z y x dS w n m l v n m l u n m l dVU z zy zx yz y yx xzxy x V Sz zy zx yz y yx xz xy x Vzx zx yz yz xy xy z z y y x x ])()()([)()()()(δσττδτστδττσδσττδτστδττσδγτδγτδγτδεσδεσδεσδ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂-++++++++=+++++=⎰⎰⎰⎰⎰⎰⎰⎰ (f)将式(f)代入式(8.2-3),并加以整理,得])()()[(])()()[(=-+++-+++-++-+∂∂+∂∂+∂∂++∂∂+∂∂+∂∂++∂∂+∂∂+∂∂⎰⎰⎰⎰⎰dS w Z n m l v Y n m l u X n m l dV w Z zy z vY z y x u X z y x z zy zx yz y yx S xz xy x z zy zx V yz y yx xzxy x δσττδτστδττσδσττδτστδττσ因为虚位移w v u δδδ,,各自独立,而且是完全任意的,因此上列积分式中括弧内的系数均等于零,这样我们得到三个平衡方程和三个静力边界条件。