12.1 换路定律

.-换路定律————————————————————————————————作者：————————————————————————————————日期：12.1 换路定律、一阶电路的三要素法考纲要求：1、了解电路瞬态过程产生的原因。

2、掌握换路定律。

教学目的要求：1、了解电路瞬态过程产生的原因。

2、掌握换路定律。

教学重点：换路定律教学难点：换路定律课时安排：4节课型：复习教学过程：【知识点回顾】一、瞬态过程（过程）1、定义：。

2、瞬态过程产生的原因外因：。

内因：。

（元件上所储存的能量突变是产生瞬态过程的根本原因。

）二、换路定理1、换路：。

2、换路定理（1）定义：。

（2）表达式：。

3、应用电容器：换路前未储能，在换路瞬间，相当于。

换路前储能，在换路瞬间，相当于。

电感：换路前未储能，在换路瞬间，相当于。

换路前储能，在换路瞬间，相当于。

在稳态1和稳态2时，电感相当于，电容器相当于。

4、注意事项：只有和不能跃变，其他的电压和电流可以跃变。

5、电压、电流初始值的计算（1）；（2）；（3） ；（4） ；【课前练习】一、判断题1、发生过渡过程时，电路中所有电流、电压均不能发生突变。

( )2、在电路的过渡过程中，电感中的电流和电容两端的电压是不能突变的。

( )3、在电路的换路瞬间，电感两端电压和电容中的电流是可以突变的。

( )4、换路定律不仅适用于换路的瞬间，也适用于瞬态过程中。

( )5、电路的瞬态过程是短暂的，其时间的长短是由电路的参数决定的。

( )6、电路中只要有储能元件，且进行换路，就会存在过渡过程。

( )7、电容元件的电压、电流可由换路定律确定。

( )二、选择题1、如图所示电路中，t=0时，开关闭合，若uc （0-）=0，则ic(0+)为( )A ．0B ．1AC ．2A D.∞2、如图所示电路，t=0时开关打开，则u(O+)为( )A ．25VB ．- 25VC ．OV D. 50V3、图示电路中．，t=0时开关S 闭合，那么电路中电流的初始值和稳态值分别为( )A ．iL(0+)=R E 2 iL (∞)=O ； B ．iL(0+)=O iL (∞)= RE ； C. iL(0+)=R E 2 / iL (∞)= R E ; D ．iL(0+)=R E iL (∞)= R E 2第1题图 第2题图 第3题图4、如图所示电路中，t=0时开关断开，则8Ω电阻初始电流i(0+)为 ( )A. 2A B ．- 2A C ．4A D ．- 4A5、如图所示电路中，t=0时开关打开，则uc(0+)为 ( )A ．3 VB ．-3VC ．OVD ．6V6、如图所示电路中，在已稳定状态下断开开关S ，则该电路( )A.因为有储能元件L ，产生过渡过程B ．因为电路有储能元件，且发生换路，要产生过渡过程C ．因为换路时元件L 上的电流储能不发生变化，不产生过渡过程D ．因为电路有储能元件，但不能确定是否有过渡过程第4题图 第5题图 第6题图三、填空题1、电路产生瞬态过程的充分条件是,必要条件是(1) ，(2) .2、RL串联电路，已知，L=2H，R=4Ω，iL(0-)=2 A，在t=0时闭合开关S对电阻R放电，则电阻R在此放电过程中吸收的能量为，电感元件在未放电前储存的能量为。

线性动态电路换路定律一、过渡过程的概念1. 过渡过程的概念电路从一种稳定状态变化到另一种稳定状态的中间过程叫做电路的过渡过程。

实际电路中的过渡过程是暂时存在最后消失,故又称为暂态过程,简称暂态。

2. 产生过渡过程的原因①内因：电路中有储能元件（电感或电容）②外因：换路在电路理论中，通常把电路状态的改变（如通电、断电、短路、电信号突变、电路参数的变化等），统称为换路，并认为换路是立即完成的。

二、换路定律1. 电路基本定律：基尔霍夫定律和欧姆定律2. 换路定律：①概念：a.为换路瞬间b.表示换路前的终了时间c.表示换路后的初始瞬间d.三者关系：②换路定律内容：a.电感元件:由于它所储存的磁场能量在换路的瞬间保持不变，否则将产生无穷大的功率，因此可得b.电容元件:由于它所储存的电场能量在换路的瞬间保持不变，否则将产生无穷大的功率，因此可得说明：在换路时，只是电容电压和电感电流不能突变，而电路中其它的电压和电流是可以突变。

三、换路定律的应用：求电路初始值1.概念①一阶电路：只含有一个（或等效化简为一个）储能元件，可以用一阶微方程描述的电路，称为一阶电路。

②初始值：把时刻电路中电压、电流的值，称为初始值，简称初值。

2.求初始值步骤①求：、作时电路，直流电路中：电容用开路替换，电感用短路来替换。

求换路前瞬间电容电压和电感电流值；②由换路定律求：、、；③作时的等效电路：把C用电压源替换，把L用电流源替换；如果，电容用短路导线替换，若，电感用开路来替换。

④由时的等效电路求电路其它电压和电流在时的初始值。

四、应用举例例6.1 图6.1（a）所示电路中, 已知U s=12V, R1=4kΩ, R2=8kΩ, C=1μF, 开关S原来处于断开状态, 电容上电压。

求开关S闭合后, t=0+时, 各电流及电容电压的数值。

解选定有关参考方向如图所示。

(1) 由已知条件可知: 。

(2) 由换路定律可知: 。

(3) 画出t=0+时刻的等效电路, 如图6.2（b）所示。

暂态和换路定则 - 电工基础
一、暂态
1、暂态的定义、产生的缘由
电路的工作状态包括：稳态和暂态。

稳态：指电路中的电压和电流在给定的条件下已达到某一稳态值（对沟通来讲是其幅值达到稳定），如第一、二章所述的电路。

暂态：指电路在过渡过程中的工作状态。

（1）概念：
过渡过程：从一个稳定状态过渡到另一个稳定状态的中间过程称为过渡过程，亦称其为暂态过程。

（2）过渡过程产生的缘由
①内因：系统中的能量不能发生跃变。

电路中的电场能和磁场能不能发生跃变是电路产生过渡过程的根本缘由。

②外因或条件：换路。

即开关接通、断开，电路的参数变化，电源电压变化等等是电路产生过渡过程的外部条件。

2、争辩电路暂态的目的
①生疏和把握其规律，在生产上充分利用暂态过程的特性：如利用电路的暂态过程产生特定波形的电信号，如锯齿波，三角波，尖脉冲波等，应用于电子线路。

②同时预防它所产生的危害：如防止电路产生过电压或过电流损坏用电设备，如电感线圈中的暂态过程产生过电压使开关产生电弧或击穿线圈绝缘；电容电路过渡过程产生过电流使电流表损坏等等。

二、换路定则
电源（开关）的接通与断开或电路结构、参数的发生突变统称为换路。

t＝0换路时刻（瞬间）t＝0_换路前终了瞬间，一般看作稳态 u(0-)，i(0-)t＝0+换路后初始瞬间，变化开头时刻 u(0+)，i(0+) 电感任意时刻存储的磁场能
―i：任意时刻流过电感的电流。

电容任意时刻存储的电场能
―u：任意时刻电容两端的电压。

依据能量不能跃变，在电路中有：
(a) 电感中的电流不能跃变：
(b) 电容两端的电压不能跃变：
换路定则：。

简述电容换路定律和电感换路定律的主要内容电容换路定律和电感换路定律是电路中常用的两个重要定律，它们分别描述了电容和电感在电路中的作用和特性。

下面将分别对这两个定律进行简要的介绍。

一、电容换路定律电容换路定律是电容器在电路中的一条基本规律，它描述了电容器在电路中充电和放电的过程。

根据电容换路定律，当电容器接入电路时，电容器会开始充电，直到达到与电源电压相等的电压。

在充电过程中，电容器的电流会逐渐减小，直到最终停止充电。

电容换路定律的核心思想是电容器充电过程中的电流与电压之间的关系。

根据欧姆定律和电容器的电流-电压关系，我们可以得到电容换路定律的数学表达式。

假设电容器的电压为V，电容器的电流为I，电容器的电容为C，则电容换路定律可以表示为I = C * dV/dt，其中dV/dt表示电压随时间的变化率。

电容换路定律的应用非常广泛。

在电子电路中，电容器常常被用来存储和释放电荷，从而实现信号的滤波和延时等功能。

此外，电容换路定律也被广泛应用于电源管理和能量转换等领域。

二、电感换路定律电感换路定律是电感器在电路中的一条基本规律，它描述了电感器在电路中储存和释放能量的过程。

根据电感换路定律，当电感器接入电路时，电感器会开始储存能量，直到达到与电源电流相等的电流。

在储能过程中，电感器的电压会逐渐增加，直到最终停止储能。

电感换路定律的核心思想是电感器储能过程中的电压与电流之间的关系。

根据欧姆定律和电感器的电流-电压关系，我们可以得到电感换路定律的数学表达式。

假设电感器的电流为I，电感器的电压为V，电感器的电感为L，则电感换路定律可以表示为V = L * dI/dt，其中dI/dt表示电流随时间的变化率。

电感换路定律的应用也十分广泛。

在电子电路中，电感器常常被用来储存和释放能量，从而实现信号的滤波和放大等功能。

此外，电感换路定律也被广泛应用于电磁感应和电动机等领域。

电容换路定律和电感换路定律是电路中的两个重要定律，它们分别描述了电容器和电感器在电路中的作用和特性。

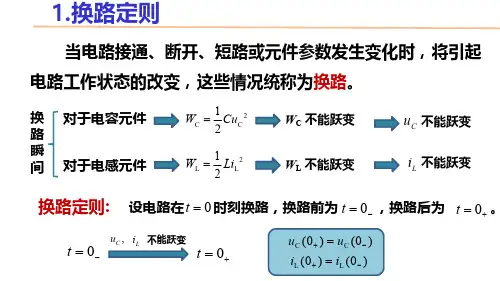
1.换路定则当电路接通、断开、短路或元件参数发生变化时，将引起电路工作状态的改变，这些情况统称为换路。

对于电容元件 2C C 12W Cu =W C 不能跃变C u 不能跃变对于电感元件 W L 不能跃变L i 不能跃变换路瞬间换路定则:C C L L (0)(0)(0)(0)u u i i +-+-==2LL 21Li W =设电路在 时刻换路，换路前为 ，换路后为 。

-=0t 0=t +=0t -=0t +=0t 不能跃变,C u L i2. 电压、电流初始值的确立求解步骤：先由 的电路求出 或 ，然后再由 的电路在已求得的 或 条件下求其它电压和电流的初始值。

-=0t +=0t )0(-C u )0(-L i )0(+C u )0(+L i 在求其它电压和电流初始值时：（1）若储能元件换路前有储能，可将电容元件视为一个恒压源（电压值为 ），电感元件视为一个恒流源（电流值为 ）； )0(+C u )0(+L i C (0)0u +=0)0(L =+i （2）若储能元件未储能，因 ，电容可视为短路，因 ，电感可视为开路。

【例2.1】图(a)电路原已稳定， 时开关S 断开，求换路后各电压、电流的初始值。

0=t A 1A 235)0(=+=-L i V2V 12)0(2)0(C =⨯==--L i u ,A 1)0()0(L L ==-+i i V2)0()0(C C ==-+u u A1)0()0(L -=-=++i i C V2V 14V 2)0(4)0()0(C -=⨯-=-=+-+L L i u u 0)0(=+i 【解】 由 的电路可得-0=t 换路定则时，可将电容视为2V恒压源，电感视为1A恒流源。

+=0t (a)（b) 时的等效电路+=0t【例2.2】在图（a ）中，，开关闭合前，电容器不带电荷。

电源电压 ， 时电路接通，试求换路瞬间电路中的电流和电压。

(a)【解】 由 的电路可得-=0t 换路定则Ω=Ω=Ω=3,2,1321R R R V 6=U 0=t （b) 时的等效电路+=0t 0)0(,0)0(2==--C u i 0)0()0(,0)0()0(22====-+-+C C u u i i A 6A 8313)0()0(3131=⨯+=+=++i R R R i A2A 6A 8)0()0()0(13=-=-=+++i i i V6V 16)0()0(11=⨯==++R i u L A 8A 63131)0(3131=⨯⨯+=+=+U R R R R i(a)【解】换路定则【例2.3】图(a)电路原已稳定， ，电压表内阻为 ，量程为 。

关于换路定律的证明（哈尔滨工业大学，黑龙江 哈尔滨 150001）郭男杰摘要：换路定律是描述电路过渡状态的重要定律，它表明了电容电压和电感电流的连续性，是分析一阶动态电路的理论基础。

本文重点讨论了对换路定律的证明方法。

关键词：一阶动态电路；换路定律；证明方法大多数电工学著作通过建立能量方程的方法证明u C ,i C 不能跃变。

以下是一种典型的证明过程。

以RC 串联电路为例，当它与电源接通时，储能元件的瞬时功率为p C =u C i C =u C ∙C du C dd =Cu C du C dd (1)p L =u L i L =L di L dd ∙i L =Li L di L dd (2)RC 电路若电容元件在开关闭合前未积累电荷，那么当开关闭合后，时间由0~t 时，它的端电压由0升高到u c ，其储存的电场能量则由0增长到W C =�p C dd =�Cu C du C dd u C 0=t 01Cu C 2可见电容元件的电场能量与其端电压的平方成正比。

RL 电路当开关S 闭合后，时间由0~t 时，电感元件的电流由0增大到i L ，其储存的磁场能量则由0增长到W L =�p L t 0dd =�Li L di L dd i L 0dd =12Li L 2可见电感元件的磁场能量与其通过的电流的平方成正比。

换路瞬间，储能元件的能量是不能跃变的。

对电容元件而言，W C 不能跃变，即u C 不能跃变；对电感元件而言，W L 不能跃变，即i L 不能跃变。

但是 (1)、(2)成立的前提是u C 、i L 连续，即u C 、i L 不能跃变，否则u C 、i L 不存在对时间t 的导数。

因此，在不确定u C 、i L 是否连续的情况下，不能使用它们对时间的t导数。

用这种方法证明换路定律是不合适的。

换路定律可以用局域电荷守恒定律和磁链守恒定律证明。

由电荷和磁链的连续性方程可知，电荷q、磁链ψ是时间t 的连续函数，又因为q=C u C，ψ=L i L，所以u C、i L是时间t的连续函数，即u C、i L不能跃变。

电容换路定理和电感换路定理一、引言电容和电感是电路中常见的两种元件，它们分别用来存储电荷和磁能，是电路设计和分析中的重要组成部分。

在电路中，我们经常需要根据不同的情况来改变电容和电感的连接方式，以达到我们所需的电路效果。

为了解决这个问题，电容换路定理和电感换路定理应运而生。

二、电容换路定理2.1 定义电容换路定理是指在电容器元件上，通过改变电容器连接方式来实现电路等效变换的定理。

具体地说，它是通过改变电容器两端的连接方式，将电容器从串联连接变为并联连接或从并联连接变为串联连接，来达到电路等效变换的目的。

2.2 串并联电容器的等效电容计算当电容器连接方式从串联变为并联时，其等效电容可以通过以下公式计算：C eq=C1+C2+⋯+C n当电容器连接方式从并联变为串联时，其等效电容可以通过以下公式计算：1 C eq =1C1+1C2+⋯+1C n2.3 实例分析例如，假设我们有两个电容器，一个容值为10μF，另一个容值为20μF。

如果我们将它们串联连接，则两个电容器的等效电容为：1 C eq=110μF+120μF=320μF C eq=20μF3≈6.67μF如果我们将两个电容器改为并联连接，则两个电容器的等效电容为：C eq=10μF+20μF=30μF可以看出，通过改变电容器的连接方式，我们可以得到不同的等效电容值，从而实现了电路等效变换。

三、电感换路定理3.1 定义电感换路定理是指在电感元件上，通过改变电感器连接方式来实现电路等效变换的定理。

具体地说，它是通过改变电感器的连接方式，将电感器从串联连接变为并联连接或从并联连接变为串联连接，来达到电路等效变换的目的。

3.2 串并联电感器的等效电感计算当电感器连接方式从串联变为并联时，其等效电感可以通过以下公式计算：1 L eq =1L1+1L2+⋯+1L n当电感器连接方式从并联变为串联时，其等效电感可以通过以下公式计算：L eq=L1+L2+⋯+L n3.3 实例分析例如，假设我们有两个电感器，一个电感为5mH，另一个电感为10mH。