下载文档原格式
基于数字全息技术的光学实验探究作者：吴铁飞来源：《数字技术与应用》2013年第12期摘要：数字全息技术是一项融合了光学、电学、信息技术学科的综合性技术，具有传统光学全息不可超越的优点，笔者首先分析了数字全息技术的记录和再现原理，其次通过具体的光学实例展示了数字全息技术在光学实验中记录和再现的应用。
关键词：数字全息光学实验菲涅尔全息图中图分类号：TP391.41；O438.1 文献标识码：A 文章编号：1007-9416（2013）12-0107-011 数字全息技术的基本原理数字全息技术虽然是新兴技术，但仍然秉承了传统光学全息的理念，整个过程可以分为两步：第一步，记录。
通过用CCD接受全息图，再通过使用图像采集卡将转换为数字信息的全息图存贮到电脑中；第二步，再现。
通过计算机语言编程模拟光波得到图像的再现，为了保证图像的清晰度，必须进行滤波消除衍射像。
1.1 数字全息图的记录原理数字全息的记录和再现原理图如下图1所示。
1.2 数字全息图的再现原理数字全息图的再现是指通过电脑软件进行模拟光波衍射的再现，具体步骤如下：第一步，通过数字信息再现物体和参考光波的全息波场；第二步，根据光学衍射理论，通过电脑软件进行数字模拟光波的衍射过程，同时计算再现成像平面的光波场分布情况，就能获得物体的强度像和相位像。
2 数字全息光学实验实例将数字全息技术应用于光学实验的主要目的是帮助学生理解数字全息技术的记录和再现的基本过程，通过应用光波衍射理论并通过Matlab编程实现全息图的再现，掌握新型技术的使用方法。
下述通过使用塑料色子和USAF-1951分辨率鉴别板进行数字全息技术光学实验实例，展示数字全息图的记录和再现。
2.1 实验装置组成介绍所用光源波长为532nm，单纵模固态激光器输出功率为20mW，PBS（偏振分光棱镜）与前后半波片组成分光系统，目的为了产生偏振态相同的两束光。
一束光作为参考光，另一束光照射到物体作为物光，两者经过BS（消偏振分光棱镜）合束叠加形成全息图，最后采用CMOS相机记录再现。
全息技术实验报告总结全息技术是一种利用干涉和衍射原理记录并再现物体三维图像的技术。
本次实验通过一系列实验步骤，对全息技术的原理、制作过程和实际应用进行了深入探索和实践。
以下是本次实验的总结报告。
实验目的：1. 理解全息技术的基本原理。
2. 学习全息图像的制作流程。
3. 探索全息技术在不同领域的应用。
实验原理：全息技术基于光波的干涉原理，通过记录物体对光波的干涉模式，再利用衍射原理重现物体的三维图像。
全息图像的制作通常包括两个步骤：记录和再现。
实验材料：1. 激光器：提供单色、相干光源。
2. 感光板：用于记录干涉图案。
3. 物体：作为全息图像的原型。
4. 显影剂和定影剂：用于处理感光板。
实验步骤：1. 准备实验材料，确保激光器的稳定性和感光板的清洁。
2. 将物体放置在激光器的光路上，确保物体和感光板之间的距离适当。
3. 打开激光器，让激光分为两束，一束直接照射到感光板上，另一束通过物体反射后照射到感光板上。
4. 记录干涉图案，等待感光板曝光。
5. 将感光板取出，用显影剂和定影剂处理，得到全息图。
6. 将处理后的全息图放置在激光器的光路上，观察并记录再现的三维图像。
实验结果：通过实验，成功制作了多个全息图像。
实验结果显示，全息图像能够真实地再现物体的三维形态，具有很高的分辨率和立体感。
实验分析：1. 全息技术对光源的稳定性和相干性有很高的要求，实验中激光器的稳定性对实验结果有直接影响。
2. 感光板的质量和处理过程也会影响全息图像的质量。
3. 实验中发现，物体与感光板的距离对再现图像的清晰度和立体感有显著影响。
实验结论：全息技术是一种具有广泛应用前景的三维成像技术。
通过本次实验，我们不仅掌握了全息图像的制作方法，还对全息技术的应用领域有了更深的认识。
全息技术在艺术展示、数据存储、安全防伪等领域具有重要的应用价值。
未来展望：随着技术的发展，全息技术有望在更多领域得到应用，如虚拟现实、增强现实等。
未来的研究可以进一步探索全息技术的优化方法，提高图像质量，降低成本，使其更加普及。
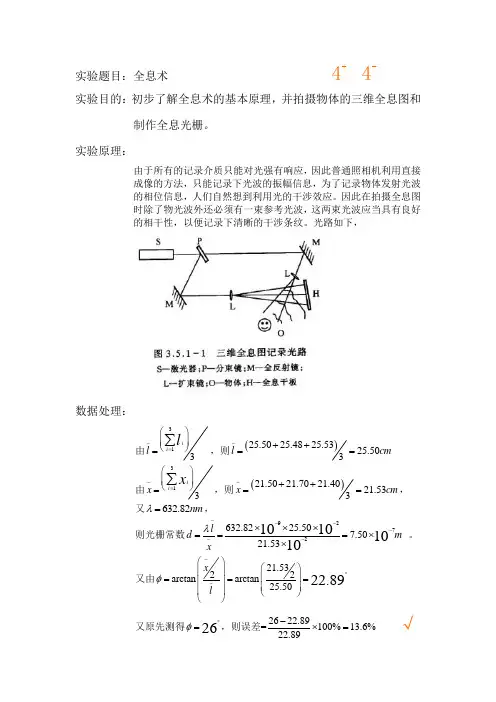
实验题目：全息术 4+ 4-实验目的：初步了解全息术的基本原理，并拍摄物体的三维全息图和制作全息光栅。
实验原理：由于所有的记录介质只能对光强有响应，因此普通照相机利用直接成像的方法，只能记录下光波的振幅信息，为了记录物体发射光波的相位信息，人们自然想到利用光的干涉效应。
因此在拍摄全息图时除了物光波外还必须有一束参考光波，这两束光波应当具有良好的相干性，以便记录下清晰的干涉条纹。
光路如下，数据处理：由313i i l l -=⎛⎫ ⎪⎝⎭=∑，则()25.5025.4825.5325.503l cm -++==由313i i x x -=⎛⎫ ⎪⎝⎭=∑，则()21.5021.7021.4021.533x cm -++==，又632.82nm λ=，则光栅常数9272632.8225.507.5021.5310101010l d m x λ------⨯⨯⨯===⨯⨯ 。
又由21.5322arctan arctan 25.5022.89x l φ-︒-⎛⎫⎛⎫ ⎪ ⎪=== ⎪ ⎪ ⎪⎝⎭⎝⎭又原先测得26φ︒=，则误差=2622.89100%13.6%22.89-⨯= √结果分析：1．全息光栅拍摄分析拍摄结果仅显示了1级和0级衍射点，由于在拍摄前已经将光路夹角尽可能的减小了，则问题可能出在光强度不足，造成此结果是由于在尽量减小夹角的操作中延长了光程，使光在传播中损耗增多。
√2．全息拍摄分析光路调节并无失误，但是第一次洗底片失败，原因是显影时间过短，按要求显影时间约2秒，但经过实际操作发现，至少8秒才能显出较清晰的图象，矫正后，第二次拍摄成功。
观察底片上物象，可见并没有十分清晰的显示出拍摄物体的全貌，原因可能是因为调整光路时没有用物体反射最强的部分进行暴光。
√PB04210263牛雷光栅衍射点对称、较亮，全息照相第一次失败，第二次较成功。
刘6/6。
基于Matlab的信息光学专题实验目录§1．基于Matlab的数字衍射光学----------01§2．计算全息实验------------------------------09§3．数字全息实验------------------------------18§4．空间频谱与空间滤波实验---------------23国承山山东师范大学物理与电子科学学院2014年4月§1 基于Matlab 的数字衍射光学§1.1、实验目的和内容初步学习Matlab 的使用。
学会用Matlab 模拟光学衍射过程。
具体实验内容：（1）. Matlab 的基本使用方法；（2）用Matlab 模拟研究光在自由空间的衍射过程；（3）；比较不同模拟算法的差别和适用条件。
§1.2、实验原理§1.2.1 光波衍射的数学模型：(1) 基于球面波叠加的衍射计算方法－点扩展函数法图1 基于球面波叠加的衍射计算模型根据惠更斯原理，入射波面可以分解成一系列具有定向传播特性的次波源，衍射光场就是这些次波源所发球面波在衍射空间的线性叠加，如图1所示。
理论分析表明，如果输入平面上光场的复振幅分布为00(,)u x y ，则该光场在距离为z 的观察屏上的衍射光场的复振幅分布(,)z u x y 可表示成下列积分形式：00(,)z u x y dx dy Σ=≈， （1）其中22(,)exp []2z ik h x y x y z ⎧⎫=+⎨⎬⎩⎭， （2）称为自由空间衍射的次波函数或点扩展函数；2/k πλ=，λ为入射光波的波长。
公式（1）通常称为菲涅耳衍射积分公式。
对（1）进行数值计算时，常常采用以下的傅立叶变换算法，即{}exp()(,)[(,)][(,)z ikz u m x n y x y u m x n y h m x n y i zδδδδδδδδλ=IDFT DFT DFT ， （3） 其中x δ和y δ为入射平面上空间坐标的抽样间隔，DFT 和IDFT 分别表示离散傅立叶积分和离散逆傅立叶积分。
数字全息综合实验实验讲义前言传统全息实验通过干涉记录与衍射再现描述了物体的振幅与相位信息，并使用银盐或光致聚合物干板做为记录介质，通过使用不同浓度、温度的药液，经过显影定影，再现物体信息，拍摄过程对环境要求较高，冲洗存在一定的安全隐患，实验结果不方便进行二次开发。
数字全息实验使用高精度CMOS 相机和空间光调制器件（SLM ）进行采集和再现，降低了对环境（暗室、防震）的要求，免去了冲洗的不安全隐患，可以对数据进行二次开发，如滤波、存储、传输、加密安全等，坧展了全息的应用领域，使经典光学再现现现代风采。
1.实验目的a.通过本实验掌握数字全息实验原理和方法；b.通过本实验熟悉空间光调制器的工作原理和调制特性；c.通过本实验理解光信息安全的概念和特点；2.实验原理全息技术利用光的干涉原理，将物体发射的光波波前以干涉条纹的形式记录下来，达到冻结物光波相位信息的目的；利用光的衍射原理再现所记录物光波的波前，就能够得到物体的振幅（强度）和位相（包括位置、形状和色彩）信息，在光学检测和三维成像领域具有独特的优势。
由于传统全息是用卤化银、重铬酸盐明胶（ DCG）和光致抗蚀剂等材料记录全息图，记录过程烦琐（化学湿处理）和费时，限制了其在实际测量中的广泛应用。
数字全息技术是由 Goodman 和 Lawrence 在 1967 年提出的，其基本原理是用光敏电子成像器件代替传统全息记录材料记录全息图，用计算机模拟再现取代光学衍射来实现所记录波前的数字再现，实现了全息记录、存储和再现全过程的数字化，给全息技术的发展和应用增加了新的内容和方法。
目前常用的光敏电子成像器件主要有电荷耦合器件 CCD、 CMOS 传感器和电荷注入器件 CID 三类。
(一 )数字全息技术的波前记录和数值重现过程可分为三部分：a.数字全息图的获取。
将参考光和物光的干涉图样直接投射到光电探测器上，经图像采集卡获得物体的数字全息图，将其传输并存储在计算机内。
第1篇一、实验目的1. 理解全息照相的基本原理和过程。
2. 掌握全息照相的实验操作技术，包括光源的选择、光路的搭建、全息图的记录与再现。
3. 通过实验观察全息图的特性，如三维立体感、干涉条纹等。
4. 分析实验中可能遇到的问题及其解决方法。
二、实验原理全息照相是一种记录和再现光波波前信息的技术。
它通过将物体反射或散射的光波（物光）与参考光发生干涉，将物光波前的振幅和相位信息以干涉条纹的形式记录在全息干板上。
当用适当的光照射全息图时，可以再现出物体的三维立体像。
全息照相的基本原理如下：1. 干涉原理：当两束相干光波相遇时，它们会相互干涉，形成明暗相间的干涉条纹。
这些条纹包含了光波的振幅和相位信息。
2. 记录原理：将物光和参考光干涉产生的干涉条纹记录在全息干板上，形成全息图。
3. 再现原理：用与参考光相干的光照射全息图，通过衍射和干涉作用，再现出物体的三维立体像。
三、实验仪器与材料1. 全息实验台2. 半导体激光器3. 分束镜（7:3）4. 反射镜5. 扩束镜6. 载物台7. 底片夹8. 被摄物体9. 全息干板10. 曝光定时器11. 显影及定影器材四、实验步骤1. 搭建光路：将激光器、分束镜、反射镜、扩束镜等仪器按照实验要求搭建好光路。
2. 选择被摄物体：将被摄物体放置在载物台上，确保其稳定。
3. 曝光：将全息干板放置在底片夹上，调整其位置，使物光和参考光在干板上形成干涉条纹。
使用曝光定时器控制曝光时间，确保干涉条纹清晰。
4. 显影与定影：将曝光后的全息干板放入显影液和定影液中处理，使干涉条纹固定。
5. 观察与记录：观察全息图上的干涉条纹，记录其特性，如条纹间距、形状等。
五、实验结果与分析1. 干涉条纹：实验中观察到的干涉条纹清晰，表明实验操作正确。
2. 再现效果：用激光照射全息图，可以看到物体的三维立体像，说明全息照相成功。
3. 影响因素：实验中发现，光路稳定性、曝光时间、显影与定影时间等因素都会影响实验结果。
实用教学型数字全息的探讨盛伟【摘要】针对传统光学全息照相技术的不足,利用激光器、CCD、反射镜以及物体搭建数字全息光路.采用数字全息照相实验为主、传统光学全息照相为辅的模式,不仅降低了全息照相技术的难度,保证实验的成功率,同时保持了实验的观赏效果.【期刊名称】《物理实验》【年(卷),期】2017(037)0z1【总页数】3页(P11-13)【关键词】全息照相;数字全息;Matlab【作者】盛伟【作者单位】南京航空航天大学理学院,江苏南京211106【正文语种】中文【中图分类】O438.1传统的光学全息照相作为大学物理实验教学的重要光学实验，因其生动有趣而受到广大学生的欢迎. 但传统光学全息光路调试相对复杂，拍摄条件要求较高[1]，且每张干板只能拍摄1次，无法保证实验的成功率. 数字全息技术采用CCD作为记录介质[2-4]，虽然可以反复拍摄全息照片，保证实验的成功率，但是普通的数字全息光路相对传统全息光路要求更高，不适合初学者，且再现物光的观赏效果也不如传统全息照片. 为了解决这些问题，本文提出了简化的数字全息光路，该光路不仅调试简单，便于学生理解全息技术，而且适用于传统全息拍摄. 因此，可采取数字全息实验为主，传统全息实验为辅的教学模式，保证成功率的前提下，保留全息再现的观赏效果.1 光路设计简化的数字全息光路如图1所示，整个光路需要激光器、CCD、反射镜以及物体. 物体与反射镜平行放置，CCD与激光器上下放置. 为了减少物光与参考光的光程差，物体与反射镜的中心点分别位于激光器的左右两侧，并且低于激光器的中心高度，高于CCD的中心高度. 为了保证反射物光与参考光的光强比，可采用反射率较高的物体，比如1元硬币等.图1 数字全息光路图激光器采用半导体激光器且自带调焦套筒[5]，改变调焦套筒中的扩束镜与点状激光源之间的距离，出射大小可调的圆形光斑. 通过合理调节激光器的调焦套筒以及物体与激光器之间的距离，保证激光同时照射反射镜与物体，分别形成参考光与物光. 最后，物光和参考光在CCD处发生干涉，并且被记录.相对常见的离轴全息光路，该光路不需要分光棱镜与扩束镜，不仅简化了光路，增强了物理模型的可理解性，而且降低了实验调节难度，更适合初次接触全息实验的学生. 但由于采用的CCD采样间隔(即像素间距)远大于全息干板的间隔，导致数字全息光路对实验条件更苛刻，因此光路中的参量必须设计得当，否则可能无法再现成像.全息技术通过记录物光与参考光的干涉条纹，然后再现成像，因此能否准确记录干涉条纹是全息拍摄的关键. 干涉条纹不仅与物平面的物光以及参考平面的参考光有关[6]，同时与2个平面的相对位置也有关. 假设图1中物光与参考光的夹角越大，则两者在CCD记录面的干涉条纹越密集，要求CCD的采样间隔越小. 因此，从CCD的采样性能来看，希望物光与参考光的夹角越小越好. 另一方面，从离轴全息的角度考虑，希望将物像、孪生像以及中央零级分离，则此夹角不能过小. 一般来说，该角度取2°～6°为宜，准确的范围由物体的大小、参考光的类型以及CCD分辨率共同决定，详细理论参见文献[7].由于物光与参考光的夹角较小，在设计光路时必须特别注意. 在本光路中想要减少夹角，可以增加物体与CCD的记录距离d和减少物体中心与反射镜中心之间的距离l. 可是距离d越大，进入CCD的物光就越弱，会降低再现物光的质量. 在实际光路中，若物体尺寸一定，则当物体紧贴反射镜时，距离l最小. 若要进一步减小距离l，可以减小物体尺寸，但物体尺寸越小，进入CCD的物光也越弱，同样会降低再现物光的质量. 因此，记录距离d以及物体大小的选择除了需要满足物光与参考光的夹角要求外，还要适当考虑成像质量.2 实验验证图1中的物体选择1元硬币的背面，因为1元硬币的背面不仅反射率较高，并且细节内容适中，因此成像质量比较理想. 兼顾物光与参考光的夹角及成像质量，记录距离d取500 mm，CCD像素间距为2.2 μm×2.2 μm，分辨率为1 944×1 944个像素点，再现的物像如图2所示. 因为硬币被黑色夹具夹持，因此被夹持的部分几乎没有反射光，所以图2中的硬币右下角出现了缺口.图2 数字全息再现图由于传统光学全息对光路的要求较数字全息低，因此相同的光路，也可以用于传统光学全息拍摄. 为了更好地显示全息的三维效果，将拍摄物体替换为小狗玩具，用相机拍摄到的再现图如图3所示，实验证明该光路的确适用于传统光学全息.图3 传统光学全息再现图另外，数字全息需要使用再现算法，且算法需要实际光路的相关参量，这些内容会增加实验的难度. 为了便于学生更专心地进行数字全息实验，利用Matlab开发友好界面的数字全息再现程序(如图4所示)，操作者只需加载全息图，测量并且输入物体与CCD的距离，即可再现成像. 如此，即使使用再现程序，也不会额外增加学生的理解难度.图4 数字全息再现程序界面3 结束语设计了简化的数字全息光路，作为实验光路，该光路原理简单易懂，配合友好界面的再现程序，适合大学物理实验教学. 由于采用CCD替换干板记录，并用电脑计算还原物像，不仅提高了实验效率，而且可以反复调试. 最后，在调试好的光路中，替换拍摄物体和记录介质，再进行光学全息照相，展示全息技术成像的三维优势. 如此不仅便于学生理解全息技术，保证了成功率，而且保留了实验原本的观赏效果.【相关文献】[1] 房若宇. 激光全息照相实验技术的改进[J]. 大学物理实验,2013,26(5):57-59.[2] 孙萍,邵明华,叶淼. 空间光调制器特性及其在数字全息中的应用[J]. 物理实验,2016,36(11):1-6.[3] 邸江磊. 用数字激光全息实验装置测量泊松比[J]. 物理实验,2013,33(10):1-4，9.[4] 盛伟,李季平. 数字成像时间平均全息振动分析[J]. 激光与光电子学进展,2014,51(4):82-86.[5] 梁霄,田源,谢瑛珂. 对全息摄影光路的一种优化[J]. 大学物理实验,2016,29(6):83-85.[6] 宋谦,杨王飞,潘永华. 提高菲涅尔全息图再现像质量的方法[J]. 物理实验,2016,36(7):32-35.[7] 贾昉. 数字全息原理及应用的研究[D]. 西安：西北大学,2008.。
数字像面全息实验数字像面全息技术可获得物体的数字显微图像,故也可称为数字显微像面全息技术，其在微观结构测量领域的应用研究具有重要意义。
它具有分辨率高、快速、非接触、无损的特点。
数字显微全息技术已发展为一种新的微观领域的测试工具, 并已应用于微机电系统/微电子机械系统检测、生物细胞测量、微观粒子成像和跟踪和聚合物粒子生长检测等领域。
数字全息过程包含两个过程:数字全息记录和数字虚拟再现。
在数字全息物理记录过程中,数字显微全息光路系统通常分无透镜系统和有透镜系统。
有透镜系统通常利用显微物镜将物体放大,将放大像看作记录物体,用CMOS （或CCD ）光敏器件数字记录微观物体放大像的物光波与参考光波的干涉场所形成的全息图,并用计算方法，计算出全息图的衍射场，数字再现得到微观物体放大的再现像。
通过对微观物体放大再现像的振幅和相位信息的定量测量,实现了对微观物场的定量测量。
当CMOS （或CCD ）光敏面置于成像系统像面上时,所记录的全息图就是物体的像面全息图。
本实验从理论上对数字像面全息进行了分析,以给出实验的理论依据。
实验目的1． 了解数字像面全息原理及其应用。
2． 记录和再现微小物体的数字像面全息图，并观察和分析获得的数字再像像。
实验原理1．数字像面全息图的记录显微像面全息记录光路的分析图如图1所示。
物体经0M 放大成像,放大的物光波与参考光波在CMOS 光敏面上干涉,并被其记录,形成物体的数字全息图。
为了便于分析,现只讨论一维情况。
忽略透镜的孔径效应,在费涅尔近轴近似条件下,记录在CMOS 上的物光波分布为o (x )={exp j k ( z 1 + z 2–d )/[2λ( z 2- d )z 1]}2/1⎰⎰o ( x 1)exp[j 12z k (x 0–x 1)2]× exp[- j f k 2x 02]exp[j )(22d z k -（x –x 0 )2]dx 1dx 0 (1) 式中,O ( x 1 ) 物场振幅透过率。
数字全息综合实验实验讲义前言传统全息实验通过干涉记录与衍射再现描述了物体的振幅与相位信息，并使用银盐或光致聚合物干板做为记录介质，通过使用不同浓度、温度的药液，经过显影定影，再现物体信息，拍摄过程对环境要求较高，冲洗存在一定的安全隐患，实验结果不方便进行二次开发。
数字全息实验使用高精度CMOS相机和空间光调制器件（SLM）进行采集和再现，降低了对环境（暗室、防震）的要求，免去了冲洗的不安全隐患，可以对数据进行二次开发，如滤波、存储、传输、加密安全等，坧展了全息的应用领域，使经典光学再现现现代风采。
1. 实验目的a.通过本实验掌握数字全息实验原理和方法；b.通过本实验熟悉空间光调制器的工作原理和调制特性；c.通过本实验理解光信息安全的概念和特点；2. 实验原理全息技术利用光的干涉原理，将物体发射的光波波前以干涉条纹的形式记录下来，达到冻结物光波相位信息的目的；利用光的衍射原理再现所记录物光波的波前，就能够得到物体的振幅（强度）和位相（包括位置、形状和色彩）信息，在光学检测和三维成像领域具有独特的优势。
由于传统全息是用卤化银、重铬酸盐明胶（DCG）和光致抗蚀剂等材料记录全息图，记录过程烦琐（化学湿处理）和费时，限制了其在实际测量中的广泛应用。
数字全息技术是由Goodman和Lawrence在1967年提出的，其基本原理是用光敏电子成像器件代替传统全息记录材料记录全息图，用计算机模拟再现取代光学衍射来实现所记录波前的数字再现，实现了全息记录、存储和再现全过程的数字化，给全息技术的发展和应用增加了新的内容和方法。
目前常用的光敏电子成像器件主要有电荷耦合器件CCD、CMOS传感器和电荷注入器件CID三类。
(一)数字全息技术的波前记录和数值重现过程可分为三部分：a.数字全息图的获取。
将参考光和物光的干涉图样直接投射到光电探测器上，经图像采集卡获得物体的数字全息图，将其传输并存储在计算机内。
b.数字全息图的数值重现。
本部分完全在计算机上进行，需要模拟光学衍射的传播过程，一般需要数字图像处理和离散傅立叶变换的相关理论，这是数字全息技术的核心部分。
c.重现图像的显示及分析。
输出重现图像并给出相关的实验结果及分析。
与传统光学全息技术相比，数字全息技术的最大优点是：(1)由于用CCD等图像传感器件记录数字全息图的时间，比用传统全息记录材料记录全息图所需的曝光时间短得多，因此它能够用来记录运动物体的各个瞬间状态，其不仅没有烦琐的化学湿处理过程，记录和再现过程都比传统光学全息方便快捷；(2)由于数字全息可以直接得到记录物体再现像的复振幅分布，而不是光强分布，被记录物体的表面亮度和轮廓分布都可通过复振幅得到，因而可方便地用于实现多种测量；(3)由于数字全息采用计算机数字再现，可以方便地对所记录的数字全息图进行图像处理，减少或消除在全息图记录过程中的像差、噪声、畸变及记录过程中CCD器件非线性等因数的影响，便于进行测量对象的定量测量和分析。
目前, 数字全息技术已开始应用于材料形貌形变测量、振动分析、三维显微观测与物体识别、粒子场测量、生物医学细胞成像分析以及MEMS器件的制造检测等各种领域。
虽然国内外在数字全息技术方面已经开展了大量的研究工作，但对于这一全息学领域的最新发展成果及其相关知识的传播和教学方面目前明显落后于科研，在全息学的实验教学上仍然以传统全息成像方法为主，很少涉及现代数字全息学知识，特别是缺少相关的数字全息实验教学仪器设备。
对此，我们设计了可用于数字全息成像实验教学的广义数字全息实验教学系统,该系统不仅包含了数字全息图记录、图像处理、重构再现的算法及其学习操作软件系统，还涉及了空间光调制器在全息再现的应用和光信息安全方面的知识，不但可以演示数字全息记录与成像过程，而且可自主学习和研究不同实验参数设置下的数字全息成像特性。
(二)数字全息记录和再现的基本理论数字全息的记录原理和光学全息一样，只是在记录时用数字相机来代替全息干板，将全息图储存到计算机内，用计算机程序取代光学衍射来实现所记录物场的数值重现，整个过程不需要在暗室中进行显影、定影等物理化学过程，真正实现了全息图记录、存储、重现和处理全过程的数字化。
a.数字全息的光路分析由于数字全息是使用数字相机代替全息干板来记录全息图，因此想要获得高质量的数字全息图，并完好地重现出物光波，必须保证全息图表面上的光波的空间频率与记录介质的空间频率之间的关系满足奈奎斯特采样定理，即记录介质的空间频率必须是全息图表面上光波的空间频率的两倍以上。
但是，由于数字相机的分辨率(约100线/mm)比全息干板等传统记录介质的分辨率(达到5000线/mm)低得多，而且数字相机的靶面面积很小，因此数字全息的记录条件不容易满足，记录结构的考虑也有别于传统全息。
目前数字全息技术仅限于记录和重现较小物体的低频信息，且对记录条件有其自身的要求，因此要想成功地记录数字全息图，就必须合理地设计实验光路。
设物光和参考光在全息图表面上的最大夹角为m ax θ，则数字相机平面上形成的最小条纹间距min e ∆为：()2sin 2max min θλ=∆e (1.1) 所以全息图表面上光波的最大空间频率为： ()λθ2sin 2max max =f (1.2)一个给定的数字相机像素大小为x ∆，根据采样定理，一个条纹周期e ∆要至少等于两个像素周期，即x e ∆≥∆2，记录的信息才不会失真。
由于在数字全息的记录光路中，所允许的物光和参考光的夹角θ很小，因此θθθ≈≈tan sin ，有：x ∆≤2λθ (1.3)所以 x∆=2max λθ (1.4) 在数字全息图的记录光路中，参考光与物光的夹角范围受到数字相机分辨率的限制。
由于现有的数字相机分辨率比较低，因此只有尽可能地减小参考光和物光之间的夹角，才能保证携带物体信息的物光中的振幅和相位信息被全息图完整地记录下来。
数字相机像素的尺寸一般在5—10m μ范围内，故所能记录的最大物参角在2—4度范围内。
只要抽样定理满足，参考光可以是任何形式的，可以使用准直光或是发散光，可以水平入射到数字相机或是以一定的角度入射。
与传统全息记录材料相比，一方面，由于记录数字全息的数字相机靶面尺寸小，仅适应于小物体的记录；另一方面，目前数字记录全息图的数字相机像素尺寸大，分辨率低，使记录的参物光夹角小，因此只能记录物体空间频谱中的低频部分，从而使重现像的分辨率低，像质较差。
综上，在数字全息中要想获得较好的重现效果，需要综合考虑实验参数，合理地设计实验光路。
b.数字全息记录和再现算法图1.1 数字全息图记录和重现结构及坐标系示意图图1.1给出了数字全息图记录和重现结构及坐标系示意图。
物体位于xoy 平面上与全息平面H H H y o x 相距d ，即全息图的记录距离，物体的复振幅分布为()y x u ,。
数字相机位于H H H y o x 面上，()H H H y x i ,是物光和参考光在全息平面上的干涉光强分布。
'''y o x 面是数值重现的成像平面，与全息平面相距'd ，也称为物平面记录面 重现面x y o ()y x u ,Hx H y Ho ()H H H y x i ,'o 'x 'y ()'',y x u z d 'd重现距离。
()'',y x u 是重现像的复振幅分布，因为它是一个二维复数矩阵，所以可以同时得到重现像的强度和相位分布。
对于图 1.1的坐标关系，根据菲涅耳衍射公式可以得到物光波在全息平面 上的衍射光场分布()H H y x O ,为：()()()()[]dxdy y y x x d jk y x u d j e y x O H H jkdH H ⎭⎬⎫⎩⎨⎧-+-=⎰⎰222ex p ,,λ (1.5) 其中λ为波长，λπ2=k 为波数。
全息平面上，设参考光波的分布为()H H y x R ,，则全息平面的光强分布()H H H y x i ,为：()()()[]()()[]*,,,,,H H H H H H H H H H H y x R y x O y x R y x O y x i +⋅+= (1.6) 其中上角标 * 代表复共轭。
用于参考光波相同的重现光波()H H y x R ,全息图时，全息图后的光场分布为()()H H H H H y x R y x i ,,⋅。
在满足菲涅耳衍射的条件下，重现距离为'd 时，成像平面上的光场分布()'',y x u 为： ()()()()()[]H H H H H H H H H jkddy dx y y x x d jk y x R y x i d j e y x u ⎭⎬⎫⎩⎨⎧-+-=⎰⎰2'2'''''2exp ,,,'λ(1.7)将(1.7)式中二次相位因子()()2'2'HH y y x x -+-展开，则(7)式可写为： ()()()()()()H H H H H H H H H H H jkd dy dx y y x x d j y x d j y x R y x i y x d j d j e y x u ⎥⎦⎤⎢⎣⎡+-⨯⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+=⎰⎰'''22'2'2'''''12exp exp ,,exp ,'λπλπλπλ(1.8)在数字全息中，为了获得清晰的重现像，'d 必须等于d （或者d -），当0'<-=d d 时，原始像在焦，重现像的复振幅分布为：()()()()()⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡+-⨯⎥⎦⎤⎢⎣⎡+--=-2212'2'''exp ,,exp ,H H H H H H H jkd y x d j y x R y x i F y x d j d j e y x u λπλπλ (1.9)同理，当0'>=d d 时，共扼像在焦，重现像的复振幅分布为：()()()()()⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡+⨯⎥⎦⎤⎢⎣⎡+=-2212'2'''exp ,,exp ,H H H H H H H jkd y x d j y x R y x i F y x d j d j e y x u λπλπλ (1.10)这样，利用傅立叶变换就可以求出重现像，这也是称之为傅立叶变换算法的原因。
在式(1.9)和(1.10)式中，傅立叶变换的频率为：d x f x λ'= dy f y λ'= (1.11) 根据频域采样间隔和空域采样间隔之间的关系，可得：H x x M f ∆=∆1 Hy y N f ∆=∆1 (1.12) 其中M 和N 分别为两个方向的采样点个数。
