2014年一次函数导学案1、2、3

第十四章一次函数14.1.1变量（41课时）文档设计者：设计时间：文档类型：文库精品文档，欢迎下载使用。

Word精品文档，可以编辑修改，放心下载学习目标：1、通过探索具体问题中的数量关系和变化规律来了解常量、变量的意义；2、学会用含一个变量的代数式表示另一个变量；学习重点：了解常量与变量的意义；学习难点：较复杂问题中常量与变量的识别学习过程：一，提出问题，创设情景问题一：汽车以60千米／小时的速度匀速行驶，行驶里程为s千米，行驶时间为t小时．２．化的量是__________．３．试用含t的式子表示s: s=________,t的取值范围是_________ .这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程．二，深入探究，得出结论（一）问题探究：问题二：每张电影票的售价为10元，如果早场售出票150张，午场售出205张，晚场售出310张，三场电影的票房收入各多少元？设一场电影售票x张，票房收入y元．•2．３．试用含x的式子表示y: y=______ ,x的取值范围是 .这个问题反映了票房收入_________随售票张数_________的变化过程．问题三：在一根弹簧的下端悬挂重物，改变并记录重物的质量，观察并记录弹簧长度的变化，探索它们的变化规律．如果弹簧原长10cm•，•每1kg•重物使弹簧伸长0．5cm，设重物质量为mkg，受力后的弹簧长度为L cm.12．３．试用含m的式子表示L: L=____________ ,m的取值范围是 .这个问题反映了_________随_________的变化过程．问题四：要画一个面积为10cm2的圆，圆的半径应取多少？圆的面积为20cm2呢？30 cm2呢?怎样用含有圆面积Ｓ的式子表示圆半径r？２．．３．试用含s的式子表示r．r=_________，s的取值范围是 . 这个问题反映了___ _ 随_ __的变化过程．问题五：用10m长的绳子围成长方形，试改变长方形的长度，观察长方形的面积怎样变化．记录不同的矩形的长度值，计算相应的矩形面积的值，探索它们的变化规律。

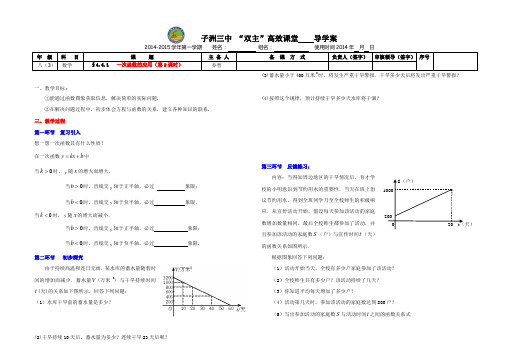
·200 100020 t （天）S （户）子洲三中 “双主”高效课堂 导学案2014-2015学年第一学期 姓名： 组名： 使用时间2014年 月 日年 级科 目课 题主 备 人 备 课 方 式 负责人（签字） 审核领导（签字） 序号 八（3） 数学§4.4.1 一次函数的应用（第2课时）乔智一、教学目标:①能通过函数图象获取信息，解决简单的实际问题.②在解决问题过程中，初步体会方程与函数的关系，建立各种知识的联系. 三、教学过程 第一环节 复习引入想一想一次函数具有什么性质？ 在一次函数y kx b =+中当0k >时，y 随x 的增大而增大，当0b >时，直线交y 轴于正半轴，必过 象限； 当0b <时，直线交y 轴于负半轴，必过 象限．当0<k 时，y 随x 的增大而减小，当0b >时，直线交y 轴于正半轴，必过 象限；当0b <时，直线交y 轴于负半轴，必过 象限. 第二环节 初步探究由于持续高温和连日无雨，某水库的蓄水量随着时间的增加而减少．蓄水量V (万米3) 与干旱持续时间t (天)的关系如下图所示，回答下列问题：（1）水库干旱前的蓄水量是多少？(2)干旱持续10天后，蓄水量为多少？连续干旱23天后呢？(3)蓄水量小于400万米3时，将发生严重干旱警报．干旱多少天后将发出严重干旱警报？(4)按照这个规律，预计持续干旱多少天水库将干涸？第三环节 反馈练习：内容：当得知周边地区的干旱情况后，育才学校的小明意识到节约用水的重要性．当天在班上倡议节约用水，得到全班同学乃至全校师生的积极响应．从宣传活动开始，假设每天参加该活动的家庭数增加数量相同，最后全校师生都参加了活动，并且参加该活动的家庭数S （户）与宣传时间t （天）的函数关系如图所示．根据图象回答下列问题：（1）活动开始当天，全校有多少户家庭参加了该活动？ （2）全校师生共有多少户？该活动持续了几天？（3）你知道平均每天增加了多少户？（4）活动第几天时，参加该活动的家庭数达到800户？ （5）写出参加活动的家庭数S 与活动时间t 之间的函数关系式第四环节 深入探究内容：1．看图填空(1)当0y =时，______x =;(2)直线对应的函数表达式是________________． 2．议一议一元一次方程0.510x +=与一次函数0.51y x =+有什么联系？第五环节 反馈练习内容：全国每年都有大量土地被沙漠吞没，改造沙漠，保护土地资源已经成为一项十分紧迫的任务，某地区现有土地面积100万千米2，沙漠面积200万千米2，土地沙漠化的变化情况如下图所示．(1)如果不采取任何措施，那么到第5年底，该地区沙漠面积将增加多少万千米2？(2)如果该地区沙漠的面积继续按此趋势扩大，那么从现在开始，第几年底后，该地区将丧失土地资源？(3)如果从现在开始采取植树造林措施，每年改造4万千米2沙漠，那么到第几年底，该地区的沙漠面积能减少到176万千米2．批改日期 月 日。

19.2.2 一次函数（第1课时）导学案【学习目标】：本节课通过问题2探索一次函数的图象及其性质，发展抽象的数学思维．能用“两点法”画出一次函数的图象。

结合图象,理解直线y=kx+b(k、b是常数,k≠0)常数k和b的取值对于直线的位置的影响。

【学习过程】：问题思索1：某登山队大本营所在地的气温为5℃，海拔每升高1km，气温下降6℃，登山队员由大本营向上登高xkm时，他们所在位置的气温是y℃，试用解析式表示y•与x的关系．【思路点拨】y随x变化的规律是，从大本营向上当海拔加xkm时，气温从5℃减少6x℃，因此y与x的函数关系为y=_________________________，•当登山队员由大本营向上登高0.5km时，他们所在位置的气温就是x=0.5时函数y=________________的值，即y=__________（℃）．问题思索2：下列问题中变量间的对应关系可用怎样的函数表示？•这些函数有什么共同点？（1）有人发现，在20～30℃时蟋蟀每分鸣叫次数C与温度t（单位：℃）有关，即C•的值约是t的7倍与35的差，其函数关系为y=___________________。

（2）一种计算成年人标准体重G（单位：千克）的方法是，以厘米为单位量出身高值h减常数105，所得差是G的值，其函数关系为y=_____________。

（3）某城市市内电话的月收费额y（单位：元）包括：月租费22元，拨打电话x分的计时费按0.01元/分收取，其函数关系为y=___________________。

（4）把一个长10cm，宽5cm的长方形的长减少x，宽不变，长方形的面积y（单位：cm2）随x的值而变化．其函数关系为y=___________________。

探索结论：1、独立思考，列出函数关系式，并进行比较，得到这一类型函数的共同特征：这些函数的形式都是自变量x的k（常数）倍与一个常数的和．2、形成概念：一般地，形如______________________的函数，叫做一次函数，当b=0时，y=kx+b即y=kx，所以说正比例函数是一种特殊的一次函数．随堂练习：课本P90练习1，2，3题．学效评价：1.下列函数中，y 是x 的一次函数的是（ ）①y=x-6；②y=x 2；③y=8x ；④y=7-x A 、①②③ B 、①③④ C 、①②③④ D 、②③④2 .写出下列函数关系中，哪些属于一次函数，其中哪些又属于正比例函数？(1)面积为10cm 2的三角形的底a(cm)与这边上的高h(cm)；(2)一边长为8(cm)的平行四边形的周长L(cm)与另一边长b(cm)；(3)食堂原有煤120吨，每天要用去5吨，x 天后还剩下煤y 吨；(4)汽车每小时行40千米，行驶的路程s （千米）和时间t （小时）．（5）汽车以60千米/时的速度匀速行驶，行驶路程中y （千米）与行驶时间x （时）之间的关系式；（6）圆的面积y （厘米2）与它的半径x （厘米）之间的关系；（7）一棵树现在高50厘米，每个月长2厘米，x 月后这棵树的高为y （厘米）同步训练：1、下列说法不正确的是( )(A)一次函数不一定是正比例函数 (B)不是一次函数就一定不是正比例函数(C)正比例函数是特定的一次函数 (D)不是正比例函数就不是一次函数2、已知函数y=(2-m)x+2m-3.求当m 为何值时,(1)此函数为一次函数?(2)此函数为正比例函数?3、一个小球由静止开始在一个斜坡向下滚动，其速度每秒增加2米。

19.2.2 一次函数 (第3课时)导学案学习目标：本节课主要探究一次函数的解析式，介绍待定系数法求一次函数解析式的方法．体会二元一次方程组的实际应用． 学习过程：活动1、引例学习已知一次函数的图像经过点（3，5）与（2，3），求这个一次函数的解析式。

分析：求一次函数b kx y +=的解析式，关键是求出k ，b 的值，从已知条件可以列出关于k ，b 的二元一次方程组，并求出k ，b 。

解： ∵一次函数b kx y +=经过点（3，5）与（2，3）∴⎩⎨⎧______________________解得⎩⎨⎧==__________b k∴一次函数的解析式为_______________像例1这样先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法，叫做________________________。

活动2、突破例4（P94）已知一次函数的图象过点（3，5）与（-4，-9），求这个一次函数的解析式．【思路点拨】求一次函数y=kx+b 的解析式，关键是求出k 、b 的值，从已知条件可以列出关于k 、b 的二元一次方程组，并求出k 、b ．【学生活动】联系已学习的二元一次方程组，以此为工具，解决问题，参与教师讲例，主动思考．解：设这个一次函数的解析式为y=kx+b ．依题意得：352491k b k k b b +==⎧⎧⎨⎨-+=-=-⎩⎩解得 这个一次函数的解析式为y=2x-1．【方法指导】引导学生归纳总结知识的流程图，提高认识．随堂练习： 课本P95练习．课堂总结：根据已知的自变量与函数的对应值，可以利用待定系数法确定一次函数解析式，具体步骤如下：1．写出函数解析式的一般形式，其中包括未知的系数（需要确定这些系数，•因此叫做待定系数）．2．•把自变量与函数的对应值（可能是以函数图象上点的坐标的形式给出）代入函数解析式中，得到关于待定系数的方程或方程组．（有几个待定系数，就要有几个方程）3．解方程或方程组，求出待定系数的值，从而写出所求函数的解析式．学效评价：1、已知一次函数2+=kx y ，当x = 5时，y = 4，（1）求这个一次函数。

一次函数导学案学习目标：1、了解一次函数图象的意义；体会一次函数与正比例函数的关系。

2、初步了解待定系数法确定自变量系数；3、能根据具体条件确定一次函数关系式中的未知数．学习重、难点：一次函数的意义与函数关系中未知数的确定.知识储备（10分钟）1、函数的定义。

2、画函数图象的步骤是①②③；3、前面所学的函数y=x+1，y=-2x-1，y=2.5x-2的图象都是什么图形？。

4、上面这几个函数关系式中的自变量的次数都是多少?它们具有什么样的一般形式？5、若点A（n，7 ）在函数y=2x+1 的图象上，则n=______。

（看书62页）新知探究一：（10分钟）一次函数的定义：上面我们讨论了这几个函数关系式都有的相同特点，即它们的自变量的次数都等于1这样的函数就是一次函数。

形如的函数叫做x的一次函数，其中，与是常数。

这里，系数k 不能为0，而b的值可以为0。

若b=0，则一次函数就变成，这样的函数也叫做正比例函数。

沙场练兵：1、下列函数关系式是一次函数的是：①y=32x-5 ( ) ②y=-0.5x ( )③y=ax+2 ( )④y=2.1x2-4 ( )⑤y=-32x( )⑥y=4-3x2( )⑦y=(a2+1)x-10( )2、判断：正比例函数是一次函数吗？一次函数是正比例函数吗？请举例说明。

新知探究二：（15分钟）自主学习课本例1. 思考：如何确定．．函数关系式（即确定函数关系式就是确定函数关系式中的的值）小组同桌讨论：确定函数关系式的一般步骤是什么？①因为y是x的一次（或正比例）函数；②所以设y=kx+b(或y=kx)(k≠0)；③把告诉的相关字母的值代入函数关系式，求出k的值；④所以函数关系式为；。

学以致用：已知一次函数y=kx-5的图象经过点M(-2,3)试求当x=4时的函数值y。

学生自主探究：如何根据函数关系式确定关系式中的未知数的值呢？。

请你来练习：已知函数y=kx-6当x=3时y的值为-5，求k的值。

子洲三中“双主”高效课堂导学案2014-2015学年第一学期姓名：组名：使用时间2014年月日年级科目课题主备人备课方式负责人（签字）审核领导（签字）序号八（3）数学§4.3.1 一次函数的图像乔智一、教学目标:1．了解一次函数的图象是一条直线，能熟练作出一次函数的图象．2．经历函数图象的作图过程，初步了解作函数图象的一般步骤：列表、描点、连线．二、教学过程第一环节：画正比例函数的图象首先我们来学习什么是函数的图象？把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标，在直角坐标系内描出它的对应点，所有这些点组成的图形叫做该函数的图象（graph）．例1 请作出正比例函数y=2x的图象．第二环节：动手操作，深化探索做一做（1）作出正比例函数y=-3x的图象．（2）在所作的图象上取几个点，找出它们的横坐标和纵坐标，并验证它们是否都满足关系y=-3x．请同学们以小组为单位，讨论下面的问题，把得出的结论写出来．（1）满足关系式y=-3x的x，y所对应的点（x，y）都在正比例函数y=-3x的图象上吗？（2）正比例函数y=-3x的图象上的点（x，y）都满足关系式y=-3x吗？（3）正比例函数y=kx的图象有何特点？你是怎样理解的？议一议既然我们得出正比例函数y=kx的图象是一条直线．那么在画正比例函数图象时有没有什么简单的方法呢？因为“两点确定一条直线”，所以画正比例函数y=kx的图象时可以只描出两个点就可以了．因为正比例函数的图象是一条过原点(0,0)的直线,所以只需再确定一个点就可以了,通常过(0,0),(1,k)作直线.例2 在同一直角坐标系内作出y=x,y=3x,y=-12x,y=-4x的图象．议一议上述四个函数中,随着x的增大,y的值分别如何变化?在正比例函数y=kx中,当k＞0时,图象在第象限，y的值随着x值的增大而 (即从左向右观察图象时,直线是向上倾斜的);当k＜0时, 图象在第象限， y的值随着x值的增大而 (即从左向右观察图象时,直线是向下倾斜的).请你进一步思考:（1）正比例函数y=x和y=3x中，随着x值的增大y的值都增加了，其中哪一个增加得更快？你能说明其中的道理吗？（2）正比例函数y=-12x和y=-4x中，随着x值的增大y的值都减小了，其中哪一个减小得更快？你是如何判断的？我们发现：k越大，直线越靠近y轴。

人教版数学初二上第14章一次函数导学案【自学目的】：了解变量的概念，会区别常量与变量．【重难点】：变量与常量，对变量的判别，找变量之间的复杂关系，试列复杂关系式学习进程：〔一〕课前预习：〔效果一：〝嫦娥二号〞进上天月转移轨道时速度是11千米/秒，假设飞行速度不变，飞行路程为s千米，飞行时间为t秒.〔2〕在以上这个进程中，变化的量是______．不变化的量是_______．〔3〕试用含t的式子表示s=_________________这个效果反映了飞行路程随飞行时间的变化进程．发现:在这个变化进程中，事先间t_____________时, 路程s就随之____________。

.效果二：上海世博会门票，每张普通票售价为160元。

〔1〕假定一天售出2万张门票，那么该天的门票支出是_______万元；〔2〕假定一天售出3万张门票，那么该天的门票支出是_______万元；〔3〕假定设一天售出x万张门票，门票支出为y万元，那么y= _______在以上这个进程中，变化的量是____________．不变化的量是____________．这个效果反映了门票支出随售出门票的变化进程．发现:在这个变化进程中，当____________确定一个值时, __________就随之确定一个值。

(二)归结概念:1、常量与变量： _____________________________________________叫常量。

____________________________________________ 叫变量。

2、指出前面三个效果中的常量、变量.〔1〕〝嫦娥飞行效果〞中s=11t，常量是____________，变量是____________；〔2〕〝世博门票效果〞中y=160x，常量是__________，变量是____________ ；3、做一做：〔1〕.某位教员为先生购置数学辅导书，书的单价是4元，那么总金额y〔元〕与先生数n〔个〕的关系式是_________。

14.2.2一次函数学习目标：1．了解两个条件确定一个一次函数；一个条件确定一个正比例函数．2．能由两个条件求出一次函数的表达式，一个条件求出正比例函数的表达式．3能根据函数的图象确定一次函数的表达式，培养学生的数形结合能力．学习重点：能根据两个条件确定一个一次函数。

学习难点：从各种问题情境中寻找条件，确定一次函数的表达式。

学习过程一．课前预习，细心认真。

一次函数关系式y＝kx＋b(k≠0)，如果知道了k与b的值，函数解析式就确定了，那么有怎样的条件才能求出k和b呢？1. 已知一个一次函数当自变量x＝-2时，函数值y＝-1,当x＝3时，y＝-3．能否写出这个一次函数的解析式呢？根据一次函数的定义，可以设这个一次函数为:y＝kx＋b(k≠0),问题就归结为如何求出k与b的值．由已知条件x＝-2时，y＝-1，得 -1＝-2k＋b．由已知条件x＝3时，y＝-3，得 -3＝3k＋b．两个条件都要满足，即解关于x的二元一次方程解得所以，一次函数解析式为2若一次函数y＝mx-(m-2)过点(0,3)，求m的值．分析考虑到直线y＝mx-(m-2)过点(0,3)，说明点(0,3)在直线上，这里虽然已知条件中没有直接给出x和y的对应值，但由于图象上每一点的坐标(x,y)代表了函数的一对对应值，它的横坐标x表示自变量的某一个值，纵坐标y表示与它对应的函数值．所以此题转化为已知x＝0时，y＝3，求m．即求关于m的一元一次方程．解答过程如下：这种先设待求函数关系式（其中含有未知的常数系数），再根据条件列出方程或方程组，求出未知系数，从而得到所求结果的方法，叫做待定系数法二．小试身手，我是最棒的！3.已知一次函数y＝kx＋b的图象经过点(-1,1)和点(1，-5),求当x＝5时，函数y的值．分析 1．图象经过点(-1,1)和点(1，-5)，即已知当x＝-1时，y＝1；x＝1时，y＝-5．代入函数解析式中，求出k与b．2．虽然题意并没有要求写出函数的关系式，但因为要求x＝5时，函数y的值，仍需从求函数解析式着手．解答过程如下：4.某物体沿一个斜坡下滑，它的速度v(米/秒)与其下滑时间t(秒 )的关系如图所示．(1)写出v与t之间的关系式；(2)下滑3秒时物体的速度是多少？分析：要求v与t之间的关系式，首先应观察图象，确定它是正比例函数的图象，还是一次函数的图象，然后设函数解析式，再把已知的坐标代入解析式求出待定系数即可．5. 已知弹簧的长度y（厘米）在一定的限度内是所挂物质量x（千克）的一次函数．现已测得不挂重物时弹簧的长度是6厘米，挂4千克质量的重物时，弹簧的长度是7.2厘米,求这个一次函数的关系式．三．当堂检测，我能做全对。

子洲三中 “双主”高效课堂 导学案2014-2015学年第一学期 姓名： 组名： 使用时间2014年 月 日年 级科 目课 题主 备 人 备 课 方 式负责人（签字） 审核领导（签字） 序号 八（3） 数学§4.4.1 一次函数的应用（第1课时）乔智一、 教学目标1.进一步训练学生的识图能力，能通过函数图象获取信息，解决简单的实际问题；2.在函数图象信息获取过程中，进一步培养学生的数形结合意识，发展形象思维； 二、教学过程： 第一环节：情境引入内容：一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题. (1)农民自带的零钱是多少?(2)试求降价前 y 与 x 之间的关系(3)由表达式你能求出降价前每千克的土豆价格是多少? (4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?第二环节：问题解决 例1小聪和小慧去某风景区游览，约好在“飞瀑”见面，上午7：00小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为 36km /h ，小慧也于上午7：00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑”，车速为26km /h ．（1）当小聪追上小慧时，他们是否已经过了“草甸”？（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少千米？内容2：深入探究例2 我边防局接到情报，近海处有一可疑船只A 正向公海方向行驶．边防局迅速派出快艇 B 追赶（如图），下图中1l ， 2l 分别表示两船相对于海岸的距离s （海里）与追赶时间t （分）之间的关系．根据图象回答下列问题：（1）哪条线表示B 到海岸的距离与时间之间的关系？海岸公海AB（2）A，B哪个速度快？（3）15 min内B能否追上A？（4）如果一直追下去，那么B能否追上A？（5）当A逃到离海岸2l海里的公海时，B将无法对其进行检查．照此速度，B能否在A逃到公海前将其拦截？第三环节：反馈练习内容：观察甲、乙两图，解答下列问题1．填空：两图中的（）图比较符合传统寓言故事《龟免赛跑》中所描述的情节．2．根据1中所填答案的图象填写下表：项目主人公（龟或兔）到达时间（分）最快速度（米/分）平均速度（米/分）红线绿线3．根据1中所填答案的图象求：（1）龟免赛跑过程中的函数关系式（要注明各函数的自变量的取值范围）；（2）乌龟经过多长时间追上了免子，追及地距起点有多远的路程？4．请你根据另一幅图表，充分发挥你的想象，自编一则新的“龟免赛跑”的寓言故事，要求如下：（1）用简洁明快的语言概括大意，不能超过200字；（2）图表中能确定的数值，在故事叙述中不得少于3个，且要分别涉及时间、路和速度这三个量．批改日期月日线型。

一次函数的图象导学案一、复习（1）什么叫一次函数？从解析式上看，一次函数与正比例函数有什么关系？。

（2）正比例函数的图象是什么？是怎样得到的？ 。

（3）正比例函数有哪些性质？是怎样得到这些性质的？ 。

二、新课（例题讲解）例1：画出一次函数y=－2x ＋1的图象解：列表描点：以表中各组对应值作为点的坐标，在直角坐标系中描出相应的点。

连线：把这些点依次连接起来。

结合图象设问:(1)一次函数的图象是什么？ 。

(2) 点（2，3）在直线y=－2x ＋1上吗？点（2，-3）呢？ 。

(3) 直线y=－2x ＋1与y 轴交点坐标是多少？与x 轴的交点做标呢？直线y=kx+b 与x 轴和y 轴交点坐标是多少？你是怎么得到的？ 。

(4) 思考：怎么简单的画一次函数的图像？ 。

三、作图探究在同一直角坐标系中分别画出一次函数y=2x ＋3，y=-x ，y=-x ＋3，y=5x-2，y=-x-3，和y=2x-3的图像。

结合你所画的函数图象回答下面几个问题：（1）、随着x 的值的增大，y 的值分别如何变化？相应图像上的点变化趋势如何？你是从那几个函数图像上看的？ 。

（合作交流）（2）直线y=2x ＋3与直线y=－x ＋3有什么共同特点？一般地，你能从函数y=kx ＋b 的图象上直接看出b 的数值吗？ 。

（合作交流）（3）完成下表（合作交流）（4）①直线y=－x 与直线y=－x ＋3，y=-x-3的位置关系如何？你能通过适当的移动将直线y=－x 变为直线y=－x ＋3和y=-x-3吗？ 。

（合作交流） ②直线y=kx 如何变化得到直线y=kx+b ？ 。

（合作交流）四、课堂练习1. 一次函数y=x-2A B C D2.下列函数中，y的值随x值的增大而增大的函数是( ).A.y=-2xB.y=-2x+1C.y=x-2D.y=-x-23.直线y=3x-2可由直线y=3x向平移个单位得到.4.直线y=-2x+4可由直线y=-2x向平移个单位得到.5. 已知一次函数y=(m-1)x+5 , 求满足下列条件的m的值：（1）函数值y 随x的增大而增大；（2）函数的图象过第一、二、四象限；五、本节课你学到了什么？自己做一个总结:。