线性定常系统的瞬态响应

1、反馈：输出信号被测量环节引回到输入端参与控制的作用。

2、开环控制系统与闭环控制系统的根本区别：有无反馈。

3、线性及非线性系统的定义及根本区别：当系统的数学模型能用线性微分方程描述时，该系统的称为线性系统。

非线性系统：一个系统，如果其输出不与其输入成正比，则它是非线性的。

根本区别：线性系统遵从叠加原理，而非线性系统不然。

4、传递函数的定义及特点：零初始条件下，系统输出量的拉斯变换与输入量的拉斯变换的比值。

用G〔s〕表示。

特点：1〕、传递函数是否有量纲取决于输入与输出的性质，同性质无量纲。

2〕、传递函数分母中S的阶数必n不小于分子中的S的阶数m，既n=>m ,因为系统具有惯性。

3〕、假设输入已给定，则系统的输出完全取决于其传递函数。

4〕、物理量性质不同的系统，环节和元件可以具有相同类型的传递函数。

5〕、传递函数的分母与分子分别反映系统本身与外界无关的固有特性和系统同外界的关系。

5、开环函数的定义：前向通道传递函数G〔s〕与反馈回路传递函数H(s)之积。

6、时间响应的定义和组成：系统在激励信号作用下，输出随时间的变化关系。

按振动来源分为：零状态响应和零输入响应。

按振动性质：自由响应和强迫响应。

7、瞬态性能指标以及反映系统什么特性：性能指标：上升时间tr、峰值时间tp、最大超调量Mp、调整时间ts、振荡次数N。

这些性能指标主要反映系统对输入的响应的快速性。

8、稳态误差的定义及计算公式：系统进入稳态后的误差。

稳态误差反映稳态响应偏离系统希望值的程度。

衡量控制精度的程度。

稳态误差不仅取决于系统自身结构参数，而且与输入信号有关。

系统误差：输入信号与反馈信号之差。

9、减少输入引起稳态误差的措施：增大干扰作用点之前的回路的放大倍数K1，以及增加这一段回路中积分环节的数目。

10、频率响应的概念：线性定常系统对谐波输入的稳态响应称为频率响应。

11、频率特性的组成：幅频特性和相频特性。

12、稳定性的概念：系统在扰动作用下，输出偏离原平衡状态，待扰动消除后，系统能回到原平衡状态〔无静差系统〕或到达新的平衡状态〔有静差系统〕。

实验二线性定常系统的瞬态响应和稳定性分析实验二、线性定常系统的瞬态响应和稳定性分析实验目的掌握线性定常系统动、静态性能的一般测试方法。

研究二阶、三阶系统的参数与其动、静态性能间的关系。

实验内容1、系统传递函数为，求系统的单位脉冲响应和单位阶跃响应解析表达式。

（1）求脉冲响应解析表达式，输入以下程序：num=[1 7 18 23 13];den=[1 5 9 7 2];G=tf(num,den);Impulse(G)[r,p,k]=residue(num,den); %应用MATLAB求传递函数的留数k=k',p=p',r=r'解得：k = 1.0000 1.0000 2.0000 2.0000p = -2.0000 -1.0000 -1.0000 -1.0000r = 1根据k、p、r的值可以写出脉冲响应C(S)的部分分式经拉普拉斯反变换有：（2）求单位阶跃响应的解析表达式由于单位阶跃响应解析，只要将G(s)的分母多项式乘以s，即分母多项式的系数向量den增加一个零，然后使用上述求脉冲响应的方法。

程序如下：num=[1 7 18 23 13];den=[1 5 9 7 2];G=tf(num,den);step(G)[r,p,k]=residue(num,[den,0]);k=k',p=p',r=r'运行结果：k = -0.5000 -5.0000 -4.0000 -2.0000 6.5000p = -2.0000 -1.0000 -1.0000 -1.0000 0r = []根据k、p、r,可以直接写出系统的阶跃响应为2、传递函数，使用MATLAB语句求系统的静态放大倍数、自然振荡频率和阻尼比。

G=tf([15],[1 6 13 20]);[wn,ksai,p]=damp(G);k=dcgain(G);k,wn=wn',ksai=ksai',p=p'运行结果：k = 0.7500 %静态系数wn = 2.2361 2.2361 4.0000 %自然振荡频率ksai = 0.4472 0.4472 1.0000 %阻尼比p = -1.0000 - 2.0000i -1.0000 + 2.0000i -4.0000 %极点3、系统的传递函数为，判断系统的稳定性。

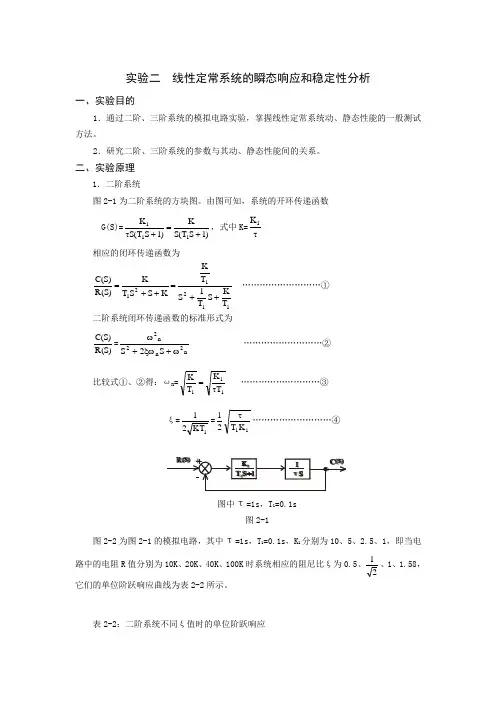
实验二 线性定常系统的瞬态响应和稳定性分析一、实验目的1．通过二阶、三阶系统的模拟电路实验，掌握线性定常系统动、静态性能的一般测试方法。

2．研究二阶、三阶系统的参数与其动、静态性能间的关系。

二、实验原理1．二阶系统图2-1为二阶系统的方块图。

由图可知，系统的开环传递函数 G(S)=)1S T (S K)1S T (S K 111+=+τ，式中K=τ1K 相应的闭环传递函数为112121T K S T 1S T KKS S T K)S (R )S (C ++=++= ………………………① 二阶系统闭环传递函数的标准形式为)S (R )S (C =n 2n 2n 2S 2S ω+ξω+ω ………………………② 比较式①、②得：ωn =111T K T K τ= ………………………③ ξ=1KT 21=11K T 21τ………………………④图中τ=1s ，T 1=0.1s图2-1图2-2为图2-1的模拟电路，其中τ=1s ，T 1=0.1s ，K 1分别为10、5、2.5、1，即当电路中的电阻R 值分别为10K 、20K 、40K 、100K 时系统相应的阻尼比ξ为0.5、21、1、1.58，它们的单位阶跃响应曲线为表2-2所示。

表2-2：二阶系统不同ξ值时的单位阶跃响应R值ξ单位阶跃响应曲线10K 0.5120K240K 1100K 1．58②模拟电路图：三、实验内容和实验数据1．二阶系统瞬态性能的测试,相关是数据填入表2-3（1）按图2-2接线，并使R分别等于100K、40K、10K用于示波器，分别观测并系统的阶跃的输出响应波形。

A.R=100KB.R=40C.R=10(2)使R=20K，(此时ξ=0.707)，然后用示波器观测系统的阶跃响应曲线，并由曲线测出超调量Mp，上升时间t p和调整时间t s。

并将测量值与理论计算值进行比较。

R=20表2-3：参数R K ωn ξ C C Mp(%) Tp(s) ts(s) 阶跃响应注意：临界状态时(即ξ=1) ts=4.7/ωn四、实验思考题1．为什么图2-1所示的二阶系统不论K 增至多大，该系统总是稳定的？答：由表2-1可知，当K 无限增大时，ξ=0；C(T )t p =2；Mp(%)=1; Tp(s)=0；ts(s)=0所以系统总是稳定的。

瞬态响应名词解释
瞬态响应是指系统在受到外部干扰时，对干扰信号的响应情况。

在实际应用中，瞬态响应对于系统的性能和稳定性非常关键。

本文将从定义、影响因素、应用场景等方面进行解释。

一、定义
瞬态响应是指系统在受到外部干扰时，对干扰信号的响应情况。

瞬态响应可以分为两种情况，一种是正常工作状态下的响应，另一种是系统从故障状态恢复后的响应。

在正常工作状态下，瞬态响应主要反映系统对瞬时干扰的响应能力；在从故障状态恢复后，瞬态响应主要反映系统恢复正常工作状态的速度和稳定性。

二、影响因素
瞬态响应受到多种因素的影响，主要包括系统的结构、参数、输入信号等。

系统的结构决定了系统对不同频率干扰的响应能力，包括系统的阻抗、传递函数等；系统的参数决定了系统的稳定性和响应速度，包括系统的阻尼比、自然频率等；输入信号的幅值、频率和相位等参数也会影响系统的瞬态响应。

三、应用场景
瞬态响应在多个领域都有着广泛的应用，包括电力系统、通信系统、控制系统等。

在电力系统中，瞬态响应主要用于评估系统对瞬时故障的响应能力，包括过电压、欠电压、瞬时断电等；在通信系统中，瞬态响应主要用于评估系统对噪声、干扰等外部信号的响应能力；在控制系统中，瞬态响应主要用于评估系统对控制信号的响应速度和稳
定性。

四、总结
瞬态响应是系统的重要性能指标之一，对系统的性能和稳定性有着重要的影响。

在实际应用中，需要根据系统的特点和应用场景来评估系统的瞬态响应能力，以保证系统的正常运行和稳定性。

线性定常系统的瞬态响应一、实验目的1．掌握线性定常系统动态性能指标的测试方法。

2．研究线性定常系统的参数对其动态性能和稳定性的影响。

二、实验设备同实验一三、实验内容1．观测二阶系统的阶跃响应，并测出其超调量和调整时间。

2．调节二阶系统的开环增益K ，使系统的阻尼比ζ=21，测出此时系统的超调量和调整时间。

3．研究三阶系统的开环增益K ，或一个惯性环节的时间常数T 的变化对系统动态性能的影响。

4．由实验确定三阶系统稳定的临界K 值。

四、实验原理本实验是研究二阶和三阶系统的瞬态响应。

为了使二阶系统的研究具有普遍性意义，通常把它的闭环传递函数写如下的标准形式：式中ζ－系统的阻尼比，n ω－系统的无阻尼自然频率。

任何的二阶系统都可以化为上述的标准形式。

对于不同的系统，它们的ζ和n ω所包含的内容也是不同的。

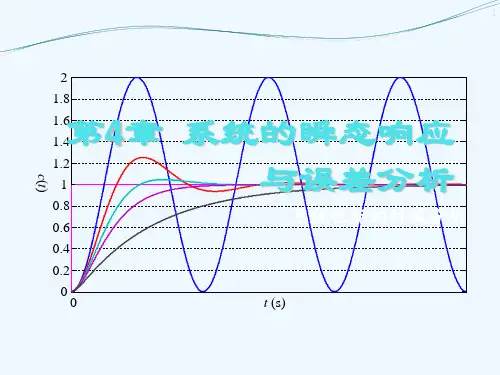
调节系统的开环增益K ，可使系统的阻尼比分别为：0<ζ<1，ζ＝1和ζ>1三种。

对应于这三种情况下系统的阶跃响应曲线，在实验中都能观测到，它们分别为附录中的图2－3所示。

本实验中的三阶系统，其开环传递函数是由两个惯性环节和一个积分环节相串连组成。

由控制理论中的劳斯判据可知，调节系统的开环增益K 和某一个惯性环节的时间常数T ，都会导致系统的稳态性能的明显变化。

有关二阶和三阶系统相关参数的理论计算和实验系统的模拟电路请参阅附录。

五、实验步骤1．利用实验平台上的通用电路单元，设计(具体可参考本实验附录的图2-2)一个由积分环节（积分环节锁零端的使用请参考实验一的相关步骤）和一个惯性环节相串联组成的二阶闭环系统的模拟电路。

待检查电路接线无误后，接通实验平台的电源总开关，并开启±5V ，±15V 直流稳压电源。

2．把采集卡接口单元的输出端DA1、输入端AD2与电路的输入端相连，电路的输出端则与采集卡接口单元中的输入端AD1相连。

连接好采集卡接口单元与PC 上位机的通信线。

华南理工大学《自动控制原理》-历年真题填空问答参考答案2005年：一．填空1.控制系统从信号传送的特点或结构形式来看，可分为开环控制和闭环控制系统。

2.闭环控制系统，对主反馈而言，只有按负反馈原理组成的闭环控制系统才能实现自动控制。

因为这种系统能使偏差越来越小，甚至被消除。

3.工程上把控制性能的要求归纳为稳定性快速性和准确性三个方面。

4.利用Routh判据判断闭环系统稳定的充分必要条件是系统特征方程的全部系数（不缺项）均为正数，且Routh 表第一列元素都是正数。

5.二阶系统，其阻尼系数等于1时，单位阶跃响应是单调衰减过程，若阻尼系数大于零小于1，单位阶跃响应是衰减的振荡过程。

6.减小或消除控制系统的稳态误差，通常可以通过增大系统的开环放大系数或增加前向通道积分环节个数来达到，但往往又会使系统的动态性能变差，甚至导致系统不稳定。

二．简答题1.线性定常系统的传递函数定义是什么？传递函数与什么有关？答：线性定常系统，在初始条件为0的条件下，输出量的拉氏变换与输入量的拉氏变换之比，称为该系统的传递函数。

传递函数表达式中各系数的值完全取决于系统的结构和参数。

2.自动控制系统稳定的定义是什么？系统稳定性与闭环极点有何关系？答：假设系统处于某一起始的平衡状态，在外作用的影响下它离开了平衡状态，当外作用消失后，经过足够长的时间它能回复到原来的平衡状态，则称该系统是稳定的。

系统稳定的充要条件是：系统的闭环极点均为负实数或（和）具有负实部的共轭复数，即系统所有闭环极点均位于复平面的虚轴左半部。

2006年一．填空1.在闭环控制系统中，通过检测元件将输出量转变成与给定信号进行比较的信号，这个信号称为反馈信号。

2.若前向通道的传递函数为()G s，反馈通道的传递函数为()H s，则开环传递函数为()()G s H s。

3.齿轮副中，以主动轮角速度ω为输入，以被动轮转角θ为输出，则这个装置为积分环节。

4.若环节的传递函数为Ks ，则其对数幅频特性()Lω在零分贝点处的频率数值为K 。

机电控制工程基础试卷及答案(填空和判断)填空题1. 传递函数的定义是对于线性定常系统,在初始条件为零的条件下，系统输出量的拉氏变换与输入量的拉氏变换之比。

2. 瞬态响应是系统受到外加作用激励后，从初始状态到最终或稳定状态的响应过程。

3. 判别系统稳定性的出发点是系统特征方程的根必须为负实根或负实部的复数根，即系统的特征根必须全部在复平面的左半平面是系统稳定的充要条件。

4. I 型系统G s K s s ()()=+2在单位阶跃输入下，稳态误差为 0 ，在单位加速度输入下稳态误差为 ∞ 。

5. 频率响应是系统对正弦输入稳态响应，频率特性包括幅频和相频两种特性。

6. 如果系统受扰动后偏离了原工作状态，扰动消失后，系统能自动恢复到原来的工作状态，这样的系统是(渐进)稳定的系统。

7. 传递函数的组成与输入、输出信号无关，仅仅决定于系统本身的结构和参数，并且只适于零初始条件下的线性定常系统。

8. 系统的稳态误差与输入信号的形式及系统的结构和参数或系统的开环传递函数有关。

传递函数反映系统本身的瞬态特性，与本身参数，结构有关，与输入无关；不同的物理系统，可以有相同的传递函数，传递函数与初始条件无关。

9. 如果在系统中只有离散信号而没有连续信号，则称此系统为离散(数字)控制系统，其输入、输出关系常用差分方程来描述。

10. 反馈控制系统开环对数幅频特性三频段的划分是以ωc （截止频率）附近的区段为中频段，该段着重反映系统阶跃响应的稳定性和快速性；而低频段主要表明系统的稳态性能。

11. 对于一个自动控制系统的性能要求可以概括为三个方面：稳定性、快速性和准确性。

1．.对控制系统的基本要求一般可以归纳为稳定性、快速性 和准确性。

2．.按系统有无反馈，通常可将控制系统分为 开环控制系统 和 闭环控制系统 。

3．.在控制工程基础课程中描述系统的数学模型有微分方程 、传递函数 动态结构图 频率特性等。

4．.稳态误差反映出稳态响应偏离系统希望值的程度，它用来衡量系统控制精度的程度。

填空题1。

传递函数的定义是对于线性定常系统,在初始条件为零的条件下,系统输出量的拉氏变换与输入量的拉氏变换之比。

2. 瞬态响应是系统受到外加作用激励后，从初始状态到最终或稳定状态的响应过程。

3。

判别系统稳定性的出发点是系统特征方程的根必须为负实根或负实部的复数根，即系统的特征根必须全部在复平面的左半平面是系统稳定的充要条件。

4. I 型系统G s K s s ()()=+2在单位阶跃输入下，稳态误差为 0 ，在单位加速度输入下 稳态误差为 ∞ 。

5。

频率响应是系统对正弦输入稳态响应，频率特性包括幅频和相频两种特性。

6。

如果系统受扰动后偏离了原工作状态，扰动消失后，系统能自动恢复到原来的工作状态，这样的系统是（渐进）稳定的系统。

7。

传递函数的组成与输入、输出信号无关，仅仅决定于系统本身的结构和参数，并且只适于零初始条件下的线性定常系统。

8. 系统的稳态误差与输入信号的形式及系统的结构和参数或系统的开环传递函数有关。

传递函数反映系统本身的瞬态特性,与本身参数，结构有关,与输入无关；不同的物理系统,可以有相同的传递函数，传递函数与初始条件无关。

9. 如果在系统中只有离散信号而没有连续信号，则称此系统为离散（数字）控制系统，其输入、输出关系常用差分方程来描述。

10. 反馈控制系统开环对数幅频特性三频段的划分是以ωc （截止频率)附近的区段为中频段，该段着重反映系统阶跃响应的稳定性和快速性;而低频段主要表明系统的稳态性能。

11。

对于一个自动控制系统的性能要求可以概括为三个方面：稳定性、快速 性和准确性.1． 。

对控制系统的基本要求一般可以归纳为稳定性、快速性 和准确性。

2． 。

按系统有无反馈，通常可将控制系统分为 开环控制系统 和 闭环控制系统 。

3． 。

在控制工程基础课程中描述系统的数学模型有微分方程 、传递函数 动态结构图 频率特性等。

4． 。

稳态误差反映出稳态响应偏离系统希望值的程度，它用来衡量系统控制精度的程度。

机械控制工程基础习题集一、填空题1、对控制系统的基本要求一般可以归纳为稳定性、（快速性）和（准确性）。

2、线性控制系统最重要的特性是可以应用（叠加）原理，而非线性控制系统则不能。

3、根据控制系统元件的特性，控制系统可分为（线性）控制系统、（非线性）控制系统。

4、反馈控制系统是根据输入量和（反馈量）的偏差进行调节的控制系统。

5、控制系统校正元件的作用是（改善系统性能）。

6、按系统有无反馈，通常可将控制系统分为（开环系统）和（闭环系统）。

7、方框图中环节的基本连接方式有串联、（并联）和（反馈）连接。

8、在控制工程基础课程中描述系统的数学模型有（微分方程）、（传递函数）等。

9、当且仅当闭环控制系统特征方程的所有根的实部都是（负数）时，系统是稳定的。

10、线性定常系统的传递函数，是在（初始条件为零）时，系统输出信号的拉氏变换与输入信号的拉氏变换的比。

11、若时间常数f(t)的拉氏变换为F(s)，当F(s)=s时，f(t)=（coswt）。

s2+w212、若输入已经给定，则系统的输出完全取决于（传递函数）。

13、当且仅当闭环控制系统特征方程的所有根的实部都是（负数）时，系统是稳定的。

14、不同属性的物理系统可以有形式相同的（数学模型）。

15、理想微分环节的输出量正比于（输入量）的微分。

16、稳定系统的时间响应分为（瞬态响应）与（稳态响应）。

17、位置误差、速度误差、加速度误差分别指输入是（阶跃）、（斜坡）和（加速度）输入时所引起的输出上的误差。

18、传递函数的组成与输入、输出信号无关，仅仅决定于（系统本身的结构和参数），并且只适于零初始条件下的（线性定常）系统。

19、线性定常系统在正弦信号输入时，稳态输出与输入的相位移随频率而变化的函数关系称为（相频特性）。

20、积分环节的对数幅频特性曲线是一条直线，其斜率为（20）dB/dec。

21、若输入已经给定，则系统的输出完全取决于（传递函数）。

22、瞬态响应是系统受到外加作用激励后，从（初始）状态到（最终或稳定）状态的响应过程。