线性定常系统的极点配置
- 格式:ppt
- 大小:1019.50 KB
- 文档页数:48



现代控制理论实验(一)线性系统的状态反馈及极点配置——09级自动化本科一.实验目的1.了解和掌握状态反馈及极点配置的原理。
2.了解和掌握利用矩阵法及传递函数法计算状态反馈及极点配置的原理与方法。
3.掌握在被控系统中如何进行状态反馈及极点配置,构建一个性能满足指标要求的新系统的方法。
二.实验原理及说明一个控制系统的性能是否满足要求,要通过解的特征来评价,也就是说,当传递函数是有理函数时,它的全部信息几乎都集中表现为它的极点、零点及传递函数。
因此若被控系统完全能控,则可以通过状态反馈任意配置极点,使被控系统达到期望的时域性能指标。
若有被控系统如图3-3-61所示,它是一个Ⅰ型二阶闭环系统。
图3-3-61 被控系统如图3-3-61所示的被控系统的传递函数为:12021S 11)1(1)(a S a S b T TS T TS S T S i i i ++=++=++=φ (3-3-51) 采用零极点表达式为:))(()(210λλφ--=S S b S (3-3-52)进行状态反馈后,如图3-3-62所示,图中“输入增益阵”L 是用来满足静态要求。
图3-3-62 状态反馈后被控系统设状态反馈后零极点表达式为:))(()(21**--=λλφS S b S (3-3-53)1.矩阵法计算状态反馈及极点配置1)被控系统被控系统状态系统变量图见图3-3-63。
图3-3-63 被控系统状态系统变量状态反馈后的被控系统状态系统变量图见图3-3-64。
图3-3-64 状态反馈后的被控系统状态系统变量图图3-3-61的被控系统的状态方程和输出方程为:状态方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧=+-=+-=••1i 1i 2211X Y u T 1X T 1X X T 1X T 1X (3-3-54)⎪⎩⎪⎨⎧=+==•∑CxY u Ax X B C B A 0),,(式中[]01,T 10B 0T 1T 1T 1A ,i i 21=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=C x x x , 被控系统的特征多项式和传递函数分别为:12010a a b S b )(+++=S S S φB A)C(SI 1--=)(A -SI det a a )(f 0120=++=S S S 可通过如下变换(设P 为能控标准型变换矩阵): —x P X =将∑0C B A ),,(化为能控标准型 ),,(————C B A ∑,即: ⎪⎩⎪⎨⎧=+=•——————x C Y u x A B X 式中 ⎥⎦⎤⎢⎣⎡-==-101a -a 10AP P A — , ⎥⎦⎤⎢⎣⎡==-10B P B 1— , []10b b CP C ==— 2)被控系统针对能控标准型),,(————C B A ∑引入状态反馈:⎥⎦⎤⎢⎣⎡=-=—————式中10k k k xk u ν (3-3-55)可求得对—x 的闭环系统),,—————C B k B A (-∑的状态空间表达式: 仍为能控标准型,即: ⎪⎩⎪⎨⎧=+-=•————————)(x C Y u x B k B A X 式中 ⎥⎦⎤⎢⎣⎡+-+-=-)()(—————1100k a k a 10k B A则闭环系统),,(——————C B k B A -∑的特征多项式和传递函数分别为: )()(—————00112k k a k a k)B (A SI det )(f ++++=⎥⎦⎤⎢⎣⎡--=S S S )k a (k a b S b B )k B A (SI C )(00112011k ———————)(+++++=⎥⎦⎤⎢⎣⎡--=-S S S φ3)被控系统如图3-3-61所示:其中:05.01==T T i则其被控系统的状态方程和输出方程为:[]XY uX X 0110012020=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=期望性能指标为:超调量M P ≤20%;峰值时间t P ≤0.5秒。



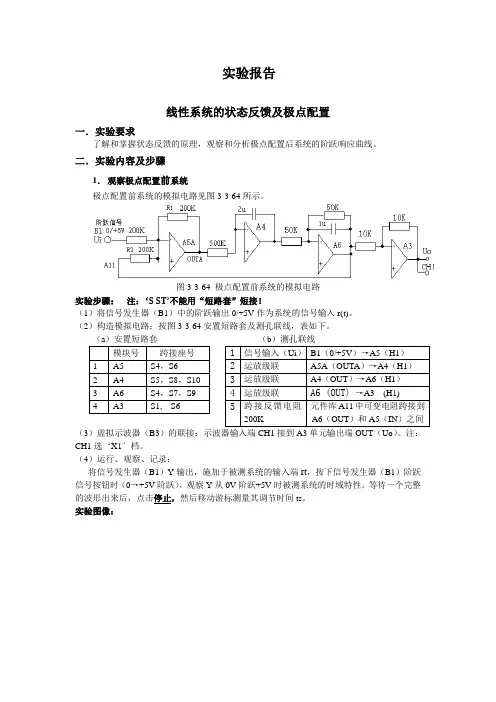
实验报告线性系统的状态反馈及极点配置一.实验要求了解和掌握状态反馈的原理,观察和分析极点配置后系统的阶跃响应曲线。
二.实验内容及步骤1.观察极点配置前系统极点配置前系统的模拟电路见图3-3-64所示。
图3-3-64 极点配置前系统的模拟电路实验步骤:注:‘S ST’不能用“短路套”短接!(1)将信号发生器(B1)中的阶跃输出0/+5V作为系统的信号输入r(t)。
(2)构造模拟电路:按图3-3-64安置短路套及测孔联线,表如下。
(3)虚拟示波器(B3)的联接:示波器输入端CH1接到A3单元输出端OUT(Uo)。
注:CH1选‘X1’档。
(4)运行、观察、记录:将信号发生器(B1)Y输出,施加于被测系统的输入端rt,按下信号发生器(B1)阶跃信号按钮时(0→+5V阶跃),观察Y从0V阶跃+5V时被测系统的时域特性。
等待一个完整的波形出来后,点击停止,然后移动游标测量其调节时间ts。
实验图像:由图得ts=3.880s 2.观察极点配置后系统 极点的计算:受控系统如图所示,若受控系统完全可控,则通过状态反馈可以任意配置极点。
受控系统设期望性能指标为:超调量M P ≤5%;峰值时间t P ≤0.5秒。
由1095.01t 707.0%5eM n n 2n p 1/p 2=≥⇒≤-==⇒≤=--ωωζωπζζζπ取因此,根据性能指标确定系统希望极点为:⎪⎩⎪⎨⎧--=+-=07.707.707.707.7*2*1j j λλ受控系统的状态方程和输出方程为:⎪⎩⎪⎨⎧=+=-----⋅-xC y b x A x μ式中][01,10,020120,21=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=----C b A x x x系统的传递函数为:202020a S a S βS β)(2012010++=+++=S S S G受控制系统的可控规范形为:[][]020T C C b T b a a T A T A X T X X C Y U b X A X K K i o K K KK k K K K ===⎥⎦⎤⎢⎣⎡==⎥⎦⎤-⎢⎣⎡-=⎥⎦⎤-⎢⎣⎡-===⎩⎨⎧=+=---10111,1020120010T ββ为变换阵),(式中当引入状态反馈阵K K =[K 0K 1]后,闭环系统()K K K K K C b K b A ,,-的传递函数为:()()()01201120120)20(20)(K S K S K a S K a S S S G o ++++=+++++=ββ而希望的闭环系统特征多项为:1001.14))(()(2*2*1**12*++=--=++=S S S S a S a S S f oλλ 令G K (S)的分母等于F #(S),则得到K K 为:[][]9.58010-==K K K k最后确定原受控系统的状态反馈阵K :由于 1-=T K K k求得和===---111,T C b T b T A T A K k K求得 ⎥⎥⎦⎤⎢⎢⎣⎡-=-1102011T所以状态反馈阵为: [][]9.59.91102019.580-=⎥⎥⎦⎤⎢⎢⎣⎡--=K极点配置系统如图所示:极点配置后系统根据极点配置后系统设计的模拟电路见下图所示。

线性系统的极点配置设计研究【引言】线性系统是现代控制工程学中的基础,系统的稳定性是控制系统设计的一个核心问题。
对于一个线性系统而言,其极点配置设计是控制系统设计中非常重要的一环。
本文将对线性系统的极点配置设计进行研究,并分别从理论和实践两个方面进行分析。
【理论分析】(一)极点概念的介绍在控制系统设计中,极点是非常重要的概念。
在数学上,一个线性系统的极点是其传递函数分母的根,通常将其表示为 s1, s2, ..., sn。
一个线性系统的稳定性与其极点有着密切的关系,当且仅当极点全部位于左半s平面才能保证系统的稳定性。
(二)极点配置设计的方法对于一个控制系统而言,其极点配置设计是控制系统设计的重点之一。
一般分为基于传递函数的极点配置设计和基于状态空间的极点配置设计两种。
1. 基于传递函数的极点配置设计传递函数的极点决定了一个系统的动态响应,因此,极点配置设计是控制系统设计中最重要的一步。
其中,将极点移动到左半s平面可以提高系统的稳定性,将极点分配到希望响应的位置可以改善系统的动态特性。
2. 基于状态空间的极点配置设计状态空间模型是控制系统设计中最常用的一种模型。
通过控制系统的状态变量的配置,可以决定其动态性能。
状态空间模型的主要优点是可以更好地对系统动态性能进行描述,因此,它是现代控制系统设计中非常重要的分析工具。
【实践分析】(一)极点配置设计的应用在实际的控制系统设计中,极点配置设计是不可或缺的环节。
针对不同的控制对象,合理地配置其极点可以有效地改善系统的动态性能。
下面列举几种常用的应用场景。
1. 直流电机系统对于直流电机系统而言,合理地配置极点可以显著提高系统的过渡过程与稳定性能。
通过使用极点配置工具,可以将系统的极点分布在希望的位置上,使得电机系统具有更好的响应速度和精度。
2. 液压伺服系统在液压伺服系统中,通过配置极点使得系统具有更好的质量指标和响应性能。
通过使用控制系统设计软件,可以更加精细地进行控制器的设计,从而提高系统的控制性能和稳定性。



线性系统的状态反馈及极点配置1.前言随着现代控制理论的不断发展和成熟,线性系统的状态反馈控制在控制理论中得到了广泛的应用,并成为了控制领域中重要的一种控制方法。
状态反馈控制能够将系统的状态进行反馈,并利用反馈得到的信息对系统进行控制,从而达到使系统达到预期控制目标的目的。
本文将从状态反馈控制的原理和实现方法两方面介绍线性系统的状态反馈及极点配置。
2.状态反馈控制的原理状态反馈控制是建立在现代控制理论的基础上的一种高级控制方法。
状态反馈控制的基本思想是在系统中引入反馈环节,设计一个反馈控制器,将系统的状态量反馈给控制器,控制器再根据反馈信号输出控制量,以期望控制系统按照预期的运动轨迹运行。
因此,状态反馈控制要实现以下两个步骤:- 系统状态量的测量:首先要在系统中安装测量传感器,实时地测量系统状态量,使得状态量可以被反馈到控制器中。
- 反馈控制器的设计:设计一个反馈控制器,将系统的状态量反馈给控制器,控制器再根据反馈信号输出控制量,实现对系统的精确控制。
因此,状态反馈控制的基本原理就是将系统状态量反馈到控制器中,以期望控制系统按照预期的运动轨迹运行。
2.2 状态空间模型与状态反馈控制状态空间模型是状态反馈控制的基础。
状态空间模型是一种方便描述线性系统动态行为和控制器的模型。
对于线性时不变系统,我们可以用如下的状态变量描述:x(t) = [x1(t),x2(t),...,xn(t)]T其中,x(t) 是系统在时刻 t 的状态量,n 是状态量的数量,x1(t),x2(t),...,xn(t) 分别是系统的每个状态量。
状态空间模型可以用一组线性常微分方程描述:dx/dt = Ax + Bu其中,A 是系统的状态方程矩阵,B 是输入矩阵,C 是输出矩阵,D 是直接耦合矩阵。
系统的状态反馈控制可以表示为:u(t) = -Kx(t)其中,K 是状态反馈矩阵。
将状态反馈控制引入到状态空间模型中,可以得到控制器的状态空间模型为:y = Cx上述控制器的状态空间模型就是一个闭环系统,通过反馈控制器将系统状态返回到系统,形成了一个反馈环。
实验报告课程名称:现代控制理论实验名称:线性系统状态反馈与极点配置一、实验目的1. 学习并掌握利用MATLAB编程平台进行控制系统设计与仿真的方法。
2. 通过仿真实验,研究并总结线性定常系统状态反馈对系统控制性能影响的规律。
3. 通过仿真实验,研究并总结状态反馈对状态不完全能控系统控制性能影响的规律。
二、实验内容(一)实验任务:1. 自行选择一个状态完全能控型SISO系统模型及参数,并设定系统控制性能指标,根据性能指标要求计算期望的极点并进行极点配置,设计MatLab实验程序(或SimuLink模拟图)及实验步骤,仿真研究状态反馈矩阵对系统控制性能的影响;2. 自行选择一个状态不完全能控型SISO系统模型及参数,并设定系统控制性能指标,根据性能指标要求进行极点配置,设计MatLab实验程序(或SimuLink模拟图)及实验步骤,仿真研究状态反馈矩阵对系统控制性能的影响;根据实验结果,总结各自的规律。
三、实验设计1.实验条件1.利用本学期所学的现代控制理论的知识为基础。
2.笔记本电脑,matlab四、实验过程1.设计状态完全能控型SISO系统模型及参数:X=(0101)X+(01)Xy=(11)Xa)首先判断系统的能控性[X XX] = [0111],是Rack([B AB]) = 2,因此此系统为可控的系统。
可以进行任意极点配置。
则期望极点配置二重根1。
b)再求状态反馈阵K=(X0 ,X1):X(x)=det[λI−(A+bK)]=X2−X1X−X0c)根据给定的极点,得到期望特征多项式:X∗(X)=(X−1)(X−1)d)比较X(x)和X∗(X)各对应项系数,可解得:X0=−1X1=2K=(−12)e)即状态反馈控制器:u=-K*x状态反馈闭环系统空间表达式x=A-B*K*xA1 = A – B*K = [0 1;1 -2]2.设计状态不完全能控型SISO系统模型及参数:X=(1001)X+(1)Xy=(11)Xa)首先判断系统的能控性[X XX] = [1100], Rank([B AB]) = 1,因此系统是不完全能控的,不能进行任意极点配置。
现代控制理论-第四章极点配置问题第四章线性定常系统的综合第四章线性定常系统的综合内容:4.1 线性反馈控制系统的基本结构及其对系统特性的影响4.2 SISO系统的极点配置4.3 系统镇定问题4.4 系统解耦问题4.5 状态观测器4.6 利用状态观测器实现状态反馈前面介绍的内容都属于系统的描述与分析。
系统的描述:主要解决系统的建模、各种数学模型(时域、频域、内部、外部描述)之间的相互转换等。
系统的分析:主要研究系统的定量变化规律(如状态方程的解,即系统的运动分析等)和定性行为(如能控性、能观测性、稳定性等)。
在本章中,将主要讨论在不同形式的性能指标下线性定常系统的反馈控制规律的综合方法,包括建立可综合的条件及建立控制规律及其算法。
综合与设计问题:在已知系统结构、参数(被控系统数学模型) 及期望的系统运动形式或特征的基础上,确定施加于受控系统的控制规律与参数,称为综合。
当系统以状态空间描述以后,系统的状态含有系统的全部运动信息。
若将控制信号设计为状态与参考信号的函数形成闭环控制,便可得到相当好的控制效果。
无论在抗扰动或抗参数变动方面,反馈系统的性能都远优于非反馈系统。
综合问题中的性能指标可区分为非优化型性能指标和优化型性能指标两种类型,它们都规定着综合所得系统运动过程的期望性能。
两者的差别是:非优化指标是—类不等式型的指标,即只要性能值达到或好于期望指标就算实现了综合目标;优化型指标则是一类极值型指标,综合目的是要使性能指标在所有可能值中取极值。
本章讨论的综合问题主要涉及的是非优化型指标,它们可能以一组期望的闭环系统极点作为性能指标,来讨论极点配置问题。
系统运动的状态也即其动态性能,主要是由系统的极点位置所决定。
把闭环极点组配置到所希望的位置上,实际上等价于使综合得到的系统的动态性能达到期望的要求。
以渐近稳定作为性能指标,主要讨论各种反馈结构对系统稳定性的影响。
使“多输入—多输出”系统实现“一个输入只控制相应的某个输出”作为性1第四章线性定常系统的综合能指标,其相应的综合问题即为解耦控制问题。
线性系统状态反馈区域极点配置算法研究摘要20世纪50年代后期,控制理论由经典控制理论向现代控制理论转变,现代控制理论是在引入状态和状态空间概念的基础上发展起来的。
与经典控制理论一样,现代控制系统中仍然主要采用反馈控制结构,但不同的是,经典控制理论中主要采用输出反馈,而现代控制系统中主要采用内部状态反馈。
状态反馈可以为系统控制提供更多的信息反馈,从而实现更优的控制。
闭环系统极点的分布情况决定于系统的稳定性和动态品质,因此,可以根据对系统动态品质的要求,规定闭环系统的极点所应具备的分布情况,把极点的配置作为系统的动态品质指标。
这种把极点配置在某位置的过程称为极点配置。
在空间状态法中,一般采用反馈系统状态变量或输出变量的方法,来实现系统的极点配置。
本论文对线性系统的状态反馈区域极点配置的算法进行了研究,分别以具有 稳定裕度和具有圆域极点约束的状态反馈控制器设计为例,利用线性矩阵不等式LMI处理方法,编写系统的MATLAB仿真程序。
最后以同样的方法对不确定系统状态反馈区域极点配置进行了研究,结果证明了设计方法的正确性和有效性。
关键词:线性系统;状态反馈;极点配置;线性矩阵不等式;不确定系统Algorithmic Research for Regional PoleAssignment of Linear System Via StateFeedback ControllersABSTRACTIn the late 1950s, control theory later by classical control theory to modern control theory shift, modern control theory is introducing state and state space concept developed on the basis of. As with classical control theory, modern control system still mainly uses the feedback control structure, but different is, classical control theory mainly uses the output feedback, and modern control system mainly uses the internal state feedback. State feedback control for system provide more information feedback, so as to achieve better control.The distribution of closed-loop system poles depends on system stability and dynamic quality, therefore, can according to the system dynamic quality request, provisions that poles of close-loop system should have the distribution of the pole, configuration of the system dynamic quality indicators. The position of the poles in the process called poles. In space, the general state method in the feedback system state variables or output variable method to achieve system poles. This thesis studied the algorithm of linear system state feedback regional poles, and respectively by the state feedback controller design of stability margin of and has round domain constraints as examples, by using the linear matrix inequality LMI treatment methods, writing MATLAB simulation program of system. Finally in the same way the uncertain system state feedback regional poles are studied, and the result shows the design method is correct and effective.Key words:Linear system;State feedback;Pole placement;LMI;Uncertain system目录摘要............................................................................................................................................ΙABSTRACT...........................................................................................................................П1 绪论 (1)1.1课题背景及意义 (1)1.2 极点配置简介 (1)1.3 本论文研究的主要工作 (2)2理论基础及数学准备 (3)2.1 区域极点配置问题 (3)2.2 状态反馈 (4)2.3 线性矩阵不等式LMI (6)2.3.1 线性矩阵不等式LMI基本变换引理 (7)2.3.2 LMI工具箱介绍 (8)2.4 本章小结 (10)3线性定常系统状态反馈区域极点配置算法研究 (11)3.1 精确极点配置 (11)3.1.1 问题描述 (11)3.1.2 算法步骤 (12)3.1.3 仿真分析 (12)3.2具有稳定裕度的区域极点配置 (15)3.2.1 问题描述 (16)3.2.2具有稳定裕度的状态反馈控制器设计 (16)3.2.3程序清单 (17)3.2.4仿真结果 (18)3.3具有圆域极点约束的状态反馈控制器设计 (21)3.3.1 问题描述 (21)3.3.2具有圆域极点约束的状态反馈控制器设计 (21)3.3.3 程序清单 (22)3.3.4仿真结果 (23)3.4 本章小结 (26)4 线性不确定系统状态反馈区域极点配置算法研究 (27)4.1 不确定性 (27)4.2线性不确定系统区域极点配置 (27)4.2.1 问题描述 (27)4.2.2 不确定系统区域极点约束的状态反馈控制器设计 (28)4.2.3 仿真分析 (30)4.3 本章小结 (32)结论 (33)致谢 (34)参考文献 (35)1 绪 论1.1 课题背景及意义在20世纪50年代蓬勃兴起的航天技术的推动下,1960年前后开始了从经典控制理论到现代控制理论的过渡,其中一个重要标志就是卡尔曼系统地将状态空间概念引入到控制理论中来。
精品文档本科毕业设计(论文)题目线性系统的状态反馈极点配置设计学院名称电气工程与自动化学院专业班级自动化08-1学生姓名导师姓名李敏年月日精品文档线性系统的状态反馈极点配置设计作者姓名专业自动化指导教师姓名李敏专业技术职务讲师目录摘要 (1)第一章绪论 (4)1.1课题背景及意义 (4)1.2本论文研究的主要工作 (4)第二章准备知识 (5)2.1极点配置简介 (5)2.2线性矩阵不等式LMI (6)2.2.1线性矩阵不等式LMI基本变换引理 (7)2.2.2 LMI工具箱介绍 (8)第三章线性定常系统精确极点配置 (11)3.1单输入精确极点配置问题 (11)3.1.1问题描述 (11)3.1.2解决方案: (11)3.2多输入精确极点配置问题 (13)3.2.1问题描述 (13)3.2.2解决方案 (13)3.3实例仿真 (13)第四章线性定常系统的区域极点配置 (15)4.1问题描述 (16)4.2解决方案 (16)4.3实例仿真 (17)第五章线性定常系统具有圆域约束的区域极点配置 (19)5.1问题描述 (19)5.2解决方案 (19)5.3实例仿真 (20)结论 (24)参考文献 (25)致谢 (26)摘要现代控制理论源于20世纪60年代,以极大值原理、贝尔曼动态规划和卡尔曼滤波技术为形成标志,经典理论中以单一输入变量为研究对象,主要通过频率进行控制,现在控制理论以线性空间理论为基础,在时域中研究系统,能够定量的进行系统的分析和设计,随着计算机运算能力的发展,现代控制也在更多领域得到应用。
控制系统是由受控对象和反馈控制器两部分组成的闭环系统,经典控制理论通常采用输出反馈,而现代控制理论多采用状态反馈。
闭环系统极点的分布情况决定于系统的稳定性和动态品质,因此,可以根据对系统动态品质的要求,规定闭环系统的极点所应具备的分布情况,把极点的配置作为系统的动态品质指标。
这种把极点配置在某位置的过程称为极点配置。