ARIMAARCH模型的实证分析

基于ARIMA模型的股票价格实证分析基于ARIMA模型的股票价格实证分析一、引言随着金融市场的不断发展和股票市场的繁荣，投资者对于股票价格的预测和分析成为了热门话题。

股票价格的波动不仅受到市场供需、经济环境等因素的影响，还与投资者的行为和市场心理等因素密切相关。

因此，准确预测股票价格对投资者制定有效投资策略具有重要意义。

在众多的股票价格预测模型中，ARIMA模型因其简单易用和良好的预测效果备受关注。

二、ARIMA模型概述ARIMA模型即自回归移动平均模型(Autoregressive Integrated Moving Average Model)，是一种常用的时间序列预测模型。

该模型基于时间序列过去的值，结合自回归和移动平均的概念，对未来时间点的值进行预测。

ARIMA模型的主要思想是通过观察和分析时间序列的特性，选择合适的模型阶数，建立相关的数学模型，进而对股票价格进行预测。

三、ARIMA模型的应用1. 数据的获取与预处理为了获取股票价格的时间序列数据，可以通过公开的金融数据库或股票交易所进行下载。

获取到数据后，需要对数据进行清洗和预处理，包括去除缺失数据和异常值等。

2. 时间序列的平稳性检验ARIMA模型对于时间序列的平稳性有一定的要求，即序列的均值和方差不随时间变化而发生显著变化。

通过统计学方法或绘制时间序列图进行观察，可以初步判断时间序列的平稳性。

如果序列不平稳，需要进行差分操作，直到时间序列达到平稳。

3. 模型训练和参数估计基于前面步骤得到的平稳时间序列，根据ARIMA模型的建模原则，选择合适的模型阶数。

ARIMA模型有三个参数：p（自回归阶数）、d（差分阶数）和q（移动平均阶数）。

利用最大似然估计等方法，通过计算得出模型参数的最优估计值。

4. 模型的验证和检验模型的验证和检验主要包括残差检验和模型拟合度的评估。

对于残差，可以通过对其进行ACF和PACF图的观察，判断其是否满足随机性和平稳性的要求。

基于ARIMA模型的上证指数分析与预测的实证研究张颖超;孙英隽【摘要】近年来,我国资本市场快速发展,其中股票市场吸引了大量的资金.而股价作为反映企业经济实力、发展水平的重要指标,受到了人们越来越多的关注.上证指数作为一个综合反映股市变动情况的指标,有利于市场参与者对市场进行分析.因此,选取2016年2月1日至2018年10月16日的上证指数收盘价作为研究数据,建立ARIMA模型,对未来的上证指数进行预测和分析,以期为广大投资者提供投资指标,为企业政策决定者提供可靠的依据.【期刊名称】《经济研究导刊》【年(卷),期】2019(000)011【总页数】5页(P131-135)【关键词】ARIMA模型;预测;时间序列;上证指数【作者】张颖超;孙英隽【作者单位】上海理工大学管理学院,上海 200093;上海理工大学管理学院,上海200093【正文语种】中文【中图分类】F830.91引言早在数百年前，随着股份公司这种企业组织形态在资本主义国家诞生，股票就随之诞生。

随着我国资本市场的快速发展，股票市场吸引到大量的资金，受到人们越来越多的关注。

上证指数由上海证券交易所编制，以上海证券交易所挂牌上市的全部股票为计算范围，综合反映了上海证券交易市场的总体走势，能够在一定程度上反映国家的经济发展水平、企业的经济实力，以及广大个人投资者的收入水平，是一个全面的、综合的重要经济衡量指标。

因此，通过对上证指数的短期预测可以为大量投资者提供投资指标，给企业政策决定者可信的依据。

然而，股票市场风云莫测、起起伏伏、波动巨大，很难对其长期走势进行长期精准的预测。

目前，预测股票价格走势的方法多种多样，但是均存在对股票价格的波动拟合效果较差、预测精度有限等问题。

由于时间序列模型具有应用范围广、限制要求低、短期预测准确率高等优点，因此时间序列模型已经成为金融预测领域较流行的预测模型之一。

本文选取2016年2月1日至2018年10月16日的上证指数数据，经过反复测试，建立 ARIMA（4，1，4）模型，对未来进行短期预测。

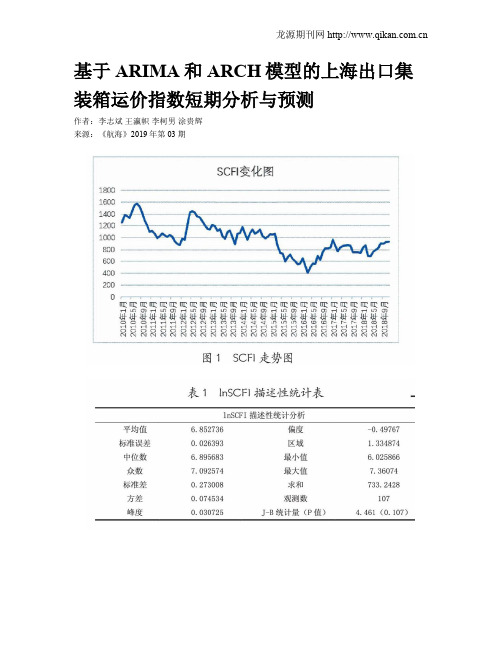
基于ARIMA和ARCH模型的上海出口集装箱运价指数短期分析与预测作者：李志斌王瀛帜李柯男涂贵辉来源：《航海》2019年第03期摘; 要：上海出口集装箱运价指数（SCFI）是反映市场运价指数行情变化趋势的主要指标。

本文首先运用ADF检验对SCFI序列进行检验，得出SCFI序列是一个单位根过程，是非平稳的;然后，对SCFI 序列进行一阶差分，差分后是平稳的，通过构建ARIMA模型，得出SCFI的ARIMA（2，1，2）模型。

针对SCFI指数的波动性，研究其对数序列ln（SCFI），通过ADF检验判断ln（SCFI）序列也是一阶单整的。

最后，运用ARCH LM检验得出SCFI对数序列存在ARCH效应，并用ARCH （1，1）模型消除残差序列的条件异方差性。

利用Eviews 软件和Crystal ball进行实践操作，对研究问题进行求解，旨在了解上海出口集装箱运输市场形式，判断市场走向，为相关港航企业经营决策以及政府部门调控管理提供参考。

关键词：上海出口集装箱运价指数;ADF检验;ARIMA模型;ARCH模型1 绪论1.1 研究背景上海是国际知名的贸易物流中心，位于东南沿海，地理位置优越，邻近国际航运主干道，适宜建设港口，依托长三角作为经济腹地，每年都有大量的集装箱货物完成进出口贸易。

上海港理所当然地承担起集装箱进出口枢纽的责任，近些年的集装箱吞吐量在世界范围内名列前茅，从2010年起到2018年，已经连续9年坐稳全球第一的宝座。

为更好地反映上海的集装箱运输市场水平，上海出口集装箱运价指数（SCFI）由此而生，通过分析运价指数的影响因素以及波动情况，可以更好地了解运输市场的价格趋势，控制价格水平，使集装箱运输市场平稳良好地发展，最大限度地发挥运价指数的指导性作用，为我国航运企业提出运价参考，增强上海在建设国际航运中心的竞争优势，乃至对于推动上海国际航运中心建设具有重大战略意义。

1.2 研究内容本文的主要内容：第一章介绍了研究SCFI的背景，基于国内外对BDI，CCFI的研究现状，确定了本文的研究思路以及研究方法。

ARIMA模型在我国居民消费价格指数的实证分析作者：方羽来源：《行政事业资产与财务》2020年第10期摘要：本文关注我国居民消费价格指数，结合我国1985-2018年数据对居民消费价格指数进行ARIMA模型的拟合并预测2019年我国居民消费价格指数，并结合实际情况，提出一些意见和建议。

关键词：HP滤波法;ARIMA模型;居民消费价格指数居民消费价格指数（CPI），是一个反映居民购买一般消费品和服务的价格水平变动情况，属于一种宏观经济指标。

且其变动率在一定程度上反映了我国经济发展的通货膨胀或紧缩程度，是关系国计民生的一项重要指标。

关注居民消费价格指数，关注其变动发展情况是反映我国物价水平的重要方面。

一、我国居民消费指数基本情况自1985年以来，我国居民消费价格指数（上一年=100）不断变动，但整体基本维持在100以上，及较上一年有所增长，34年来平均居民消费价格指数为105.27。

在2000年以前，我国居民消费指数变动很明显，1985€？994年呈现先增长后下降再急速增长的态势，且于1994年达到近34年来的峰值124.1。

1995€？998年持续下降，且将至近34年的最小值，仅98.6。

2000年以后的居民消費指数变动明显不如2000年以前大，但仍有起伏波动。

2012年以后居民消费指数趋于稳定但仍有小幅变动。

二、HP滤波法（1）数据来源。

本文数据源自《中国统计年鉴》（2000€？019年）选择1985€？018年的居民消费指数数据（上一年=100），共计34个数据，其中1985€？016年用于拟合模型，2017和2018年数据用于模型检验。

（2）HP滤波法实证分析。

利用HP滤波法，可将居民消费指数数据可以看作由趋势成分和波动成分两者组成的，通过设定一个损失函数，并结合事先给定的取值，使损失函数最小化，将居民消费指数数据分解为趋势成分和波动成分，前者代表CPI指数的长期变动，后者代表CPI指数的短期波动。

光伏建筑一体化行业板块指数的预测模型构建——基于ARIMA模型的实证分析光伏建筑一体化行业板块指数的预测模型构建——基于ARIMA模型的实证分析摘要：本文旨在构建光伏建筑一体化行业板块指数的预测模型，并使用ARIMA模型进行实证分析。

首先，通过收集相关数据以及分析光伏建筑一体化行业的特征，确定了ARIMA模型的适用性。

然后，利用Python编程语言中的statsmodels库进行ARIMA 模型的建模和分析。

最后，通过对比模型预测结果与实际观测值，验证了所构建模型的准确性和有效性。

关键词：光伏建筑一体化；行业板块指数；ARIMA模型；预测模型1. 引言光伏建筑一体化作为一种新兴的可再生能源利用方式，凭借其绿色、环保的特点，受到越来越多的关注。

光伏建筑一体化产业链涉及光伏组件、太阳能电池、建筑材料等多个领域，是一个复杂的产业体系。

为了更好地了解和监测光伏建筑一体化行业的发展趋势，建立行业指数具有重要意义。

本文将使用ARIMA模型对光伏建筑一体化行业板块指数进行预测，为投资者和决策者提供参考依据。

2. 数据收集与预处理为了构建光伏建筑一体化行业板块指数的预测模型，首先需要收集相关的历史数据。

在本文中，我们选择了过去五年的行业指数数据。

接下来，对收集到的数据进行预处理。

预处理的过程包括数据清洗、处理异常值和缺失值等。

通过观察数据的分布情况和统计特征，可以较好地判断是否需要进行预处理，并选择合适的方法进行处理。

3. 光伏建筑一体化行业特征分析在构建预测模型之前，需要对光伏建筑一体化行业的特征进行分析。

主要包括行业发展趋势、季节变动、周期性等。

通过对行业特征的分析，可以选择合适的模型，并对模型进行参数估计。

4. ARIMA模型介绍ARIMA模型是一种经典的时间序列预测模型，由自回归(AR)、差分(I)和滑动平均(MA)三个部分构成。

ARIMA模型根据观测值的自回归项、滑动平均项和差分项的阶数来确定。

ARIMA(p,d,q)模型中，p为自回归项阶数，d为差分次数，q为滑动平均项阶数。

BOX-JENKINS 预测法1 适用于平稳时序的三种基本模型（1）()AR p 模型（Auto regression Model ）——自回归模型p 阶自回归模型：式中，为时间序列第时刻的观察值，即为因变量或称被解释变量；，为时序的滞后序列，这里作为自变量或称为解释变量；是随机误差项；，，，为待估的自回归参数。

（2）()MA q 模型（Moving Average Model ）——移动平均模型q 阶移动平均模型：式中，μ为时间序列的平均数，但当{}t y 序列在0上下变动时，显然μ=0，可删除此项；t e ，1t e -，2t e -，…，t q e -为模型在第t 期，第1t -期，…，第t q -期的误差；1θ，2θ，…，q θ为待估的移动平均参数。

（3）(,)ARMA p q 模型——自回归移动平均模型（Auto regression Moving Average Model ）模型的形式为：显然，(,)ARMA p q 模型为自回归模型和移动平均模型的混合模型。

当q =0,时，退化为纯自回归模型()AR p ；当p =0时，退化为移动平均模型()MA q 。

2 改进的ARMA 模型（1）(,,)ARIMA p d q 模型这里的d 是对原时序进行逐期差分的阶数，差分的目的是为了让某些非平稳（具有一定趋势的）序列变换为平稳的，通常来说d 的取值一般为0,1,2。

对于具有趋势性非平稳时序，不能直接建立ARMA 模型，只能对经过平稳化处理，而后对新的平稳时序建立(,)ARMA p q 模型。

这里的平文化处理可以是差分处理，也可以是对数变换，也可以是两者相结合，先对数变换再进行差分处理。

（2）(,,)(,,)s ARIMA p d q P D Q 模型对于具有季节性的非平稳时序（如冰箱的销售量，羽绒服的销售量），也同样需要进行季节差分，从而得到平稳时序。

这里的D 即为进行季节差分的阶数；,P Q 分别是季节性自回归阶数和季节性移动平均阶数；S 为季节周期的长度，如时序为月度数据，则S =12，时序为季度数据，则S =4。

提要本文建立了 1952～2007 年中国 GDP的计量经济模型(ARIMA模型)。

对有指数趋势的原始序列用单位根法和自相关图法判别差分后序列是否平稳，先通过最小 BI C值建立计量经济模型中的时间序列模型，然后利用AI C和SBC准则判别所建立的模型是否为最优，然后用条件最小二乘法对模型的参数进行估计，并进行白噪声检验和参数显著性检验，预测2008～2015 年 GDP的发展水平。

A时间序列是指按照时间顺序得到的变量的观测值，而按时间顺序得到的经济变量的观测值即为经济时间序列。

文中讨论的 ARIMA 模型是一类常用的随机时序模型，它是一种精度较高的时序短期预测方法，其基本思想是：某些时间序列是依赖于时间 t 的一族随机变量，构成该时序的单个序列值虽然具有不确定性，但整个序列的变化却有一定的规律性，可以用相应的数学模型近似描述。

通过对该数学模型的分析研究，能够更本质地认识时间序列的结构与特征，达到最小方差意义下的最优预测。

我国 GDP 总量的形成是一个复杂的过程，受经济、政策、科技水平、自然等多因素的影响。

GDP 总量或人均 GDP 预测的理论及应用研究非常多。

国内外学者对我国GDP 的研究方法主要有三种：(1)时间序列方法：研究 GDP 随时间发展的规律。

通过时间序列的历史数据揭示现象随时间变化的规律，建立 ARMA、 ARCH 等模型，将这种规律延伸到未来，从而对该现象的未来作出预测;(2)协整检验的计量经济学模型：通过分析影响 GDP 发展的本质因素，研究 GDP 与这些因素的协整关系，建立计量经济学模型;(3)生产函势，并具有很强的非平稳性。

2、数据平稳化。

对于含有指数趋势的时间序列，可以通过取对数将指数趋势转化为线性趋势，然后再进行差分以消除线性趋势。

取对数过后的 GDP 依旧存在非平稳性，需要对其进行差分，先进行一阶差分，绘制一阶差分后的时间序列图。

从图中很难看出一阶差分后的序列是否平稳。

经济学实证研究中的时间序列分析方法比较时间序列分析是经济学实证研究中一种常用的方法，它对经济数据的时间变化进行建模和预测。

然而，由于经济学数据的特殊性和复杂性，选择合适的时间序列分析方法至关重要。

本文将比较几种常见的时间序列分析方法，包括自回归移动平均模型（ARMA）、自回归条件异方差模型（ARCH）、广义自回归条件异方差模型（GARCH）、ARIMA模型和向量自回归模型（VAR）。

ARMA模型是最基本的时间序列分析方法之一。

它假设数据的未来观测值是过去观测值的线性组合，同时考虑了残差项的随机性。

ARMA模型适用于平稳时间序列数据，其主要优点是简单易懂、计算效率高。

然而，ARMA模型无法应对非平稳时间序列数据和异方差性的存在。

ARCH模型是针对ARMA模型的不足提出的改进方法，它考虑了数据的条件异方差性。

ARCH模型假设数据的条件方差是过去观测误差的加权和，可用于对金融市场波动性进行建模。

然而，ARCH模型无法处理高度异方差的数据，且对时间序列结构的假设限制较多。

GARCH模型是ARCH模型的扩展，考虑了条件异方差和波动性的长期记忆。

GARCH模型在金融领域得到广泛应用，能够更好地对金融市场的波动进行建模。

然而，GARCH模型对参数估计的要求较高，对数据的拟合效果较为敏感。

ARIMA模型是一种广泛应用于短期时间序列预测的方法，包括自回归、差分和移动平均三个部分。

ARIMA模型能够适应一定程度的非平稳数据，并考虑了序列的趋势和季节性变化。

然而，ARIMA模型对数据具有一定的处理要求，在应用时需要仔细选择阶数和滞后期。

VAR模型是多变量时间序列分析的方法，适用于多个相关变量之间的关系分析与预测。

VAR模型的优点在于能够捕捉不同变量之间的动态联动关系，可以考虑更多的信息。

然而，VAR模型对变量之间的相关性和滞后期的选择有一定要求，模型的估计和解释较为复杂。

综上所述，经济学实证研究中的时间序列分析方法有多种选择，每种方法都有其适用的场景和局限性。

2018年6月第31卷第2期贵州商学院学报Journal of Guizhou University of CommerceJun. 2018Vol.31 No. 2基于ARIMA模型的居民消费价格指数走势实证分析与预测------以重庆市为例倪颖1，年靖宇2(1.重庆工商大学长江上游经济研究中心，重庆400067;.安徽大学经济学院，安徽合肥230601)摘要：本文选择2012年1月一2017年2月的月度同比数据，建立ARIMA模型对未来时期重 庆市城市居民消费价格指数进行预测。

分析结果显示：（1)在样本期内重庆城市居民消费价格指数与全国居民消费价格指数的走势基本一致。

（2)利用样本数据建立ARIMA(12,1，11)模型，且利用2016年11月一2017年2月的数据检验其预测精度，因其预测精度较高，可以用来预测未来期的重庆市城市居民消费价格指数。

关键词：时间序列；ARIMA模型；居民消费价格指数中图分类号：F201 文献标识码：A文章编号：1671 -9549(2018)02 -0014 -10An Empirical Analysis and Forecast of the ConsumerPrice Index Based on ARIMA Model------A Case Study of ChongqingNi Ying1,Nian Jing-yu2(1. The Upper Yangtze River Economic Research Center, Chongqing Technology And Business University, Chongqing 400067 ；2. Economics School , Anhui University , Hefei , Anhui 230601)Abstract ：This article selects the monthly year - on - year data from January 2012 to February 2017 , and establishes theARIMA model to predict the urban consumer price index of Chongqing in the future. The analysis results show that：( 1)During the sample period , the urban consumer price index of Chongqing and the national consumer price index are basi­cally consistent. (2) Using the sample data to establish the ARIMA (12,111) model , and the period 2016 to February 2017 demonstrates higher prediction accuracy , w hich is suitable to predict future urban consumer price index in Chongqing City.Key words：Time Series；ARIMA Model；Consumer Price Index引言在中国经济转型期，重庆市作为西部唯一的直辖市，且位于“一带一路”倡议和长江经济带两大国家战略的“Y形”连接点，重庆市的经济发展方式和经济结构受到显著的影响，居民的生活水平及消费需求也会受到一定程度的影响。