第7章、ARCH模型和GARCH模型教学内容
- 格式：doc
- 大小：486.00 KB
- 文档页数：51
下载文档原格式
合集下载
GARCH模型
AFra bibliotekCH模型
二、ARCH过程
Engle(1982)提出的ARCH模型，正是在不使用特定变量 xt 或数据转 换的情况下，同时对序列的均值和方差进行建模。要理解Engle的方 法，首先我们要估计平稳ARCH模型 yt a0 a1 yt 1 t 并预测 yt 1 ， 则 yt 1 的条件均值为 Et yt 1 a0 a1 yt ，若我们用这个条件均值去预 测 yt 1 ，则预测误差方差为 Et [( yt 1 a0 a1 yt )2 ] Ett21 2。 ˆt 表示模型 yt a0 a1 yt 1 t 的残差估计值，那么 yt 1的条件方 若用 差为： var( y y ) E [( y a a y )2 ] E ( )2
GRACH模型
三、GRACH模型
Bollerslev广义自回归条件异方差(Generalized ARCH,GARCH)模型。 GARCH类模型最早是Engle提出的ARCH模型，即自回归条件异方差 模型。设标的资产时间序列为{ yt } , Engle年建立了回归模型ARCH(q)，
y t 是因变量，x t 是解释变量的向量， 其中， 是未知参数的向量, 假设 t 的在给定 (t 1) 时间内的信息 t 1 满足正态分布， t | t 1 ~ N ( 0, ht ) ， 但其条件方差为：
ARCH模型
一、金融时间序列的异方差性特征
现实金融市场上，许多金融时间序列并没有恒定的均值，大多数 序列在呈现出阶段性的相对平稳的同时，往往伴随着出现剧烈的 波动性。 金融市场中，波动率（volatility）是金融时间序列最重要的特征 之一，因而模拟和预测股票市场的波动性已经成为众多理论和实 证研究的重要领域。然而，金融市场时间序列存在非平稳性，样 本均值并不恒定，有明显的异方差性特征。因此，传统线性结构 模型（以及时间序列模型）并不能很好地解释金融数据的重要特 征。
二、ARCH过程
Engle(1982)提出的ARCH模型，正是在不使用特定变量 xt 或数据转 换的情况下，同时对序列的均值和方差进行建模。要理解Engle的方 法，首先我们要估计平稳ARCH模型 yt a0 a1 yt 1 t 并预测 yt 1 ， 则 yt 1 的条件均值为 Et yt 1 a0 a1 yt ，若我们用这个条件均值去预 测 yt 1 ，则预测误差方差为 Et [( yt 1 a0 a1 yt )2 ] Ett21 2。 ˆt 表示模型 yt a0 a1 yt 1 t 的残差估计值，那么 yt 1的条件方 若用 差为： var( y y ) E [( y a a y )2 ] E ( )2
GRACH模型
三、GRACH模型
Bollerslev广义自回归条件异方差(Generalized ARCH,GARCH)模型。 GARCH类模型最早是Engle提出的ARCH模型，即自回归条件异方差 模型。设标的资产时间序列为{ yt } , Engle年建立了回归模型ARCH(q)，
y t 是因变量，x t 是解释变量的向量， 其中， 是未知参数的向量, 假设 t 的在给定 (t 1) 时间内的信息 t 1 满足正态分布， t | t 1 ~ N ( 0, ht ) ， 但其条件方差为：
ARCH模型
一、金融时间序列的异方差性特征
现实金融市场上，许多金融时间序列并没有恒定的均值，大多数 序列在呈现出阶段性的相对平稳的同时，往往伴随着出现剧烈的 波动性。 金融市场中，波动率（volatility）是金融时间序列最重要的特征 之一，因而模拟和预测股票市场的波动性已经成为众多理论和实 证研究的重要领域。然而，金融市场时间序列存在非平稳性，样 本均值并不恒定，有明显的异方差性特征。因此，传统线性结构 模型（以及时间序列模型）并不能很好地解释金融数据的重要特 征。
ARCH模型介绍
ARCH模型介绍σ_t^2=α_0+α_1*ε_(t-1)^2+α_2*ε_(t-2)^2+...+α_p*ε_(t-p)^2其中，σ_t^2表示在t时刻的波动性，α_0表示常数项，α_1,α_2,...,α_p是ARCH模型的参数，ε_t-1,ε_t-2,...,ε_t-p是t时刻的残差。
ARCH模型最重要的特点是它能够捕捉到波动性的聚集，即高波动性的时期往往会持续一段时间，而低波动性的时期也会持续一段时间。
这是因为ARCH模型中的参数可以控制波动性的趋势和持续性。
当参数值较大时，波动性的变化会更加剧烈；当参数值较小时，波动性的变化会更加平缓。
ARCH模型在金融领域特别受到关注，因为金融市场的波动性非常重要。
通过使用ARCH模型，我们可以对金融市场的波动性进行建模和预测。
例如，可以利用ARCH模型来估计股票价格的波动性，进而对股票的风险进行评估。
此外，ARCH模型还可以用于进行对冲策略的设计，以便在市场波动性较高时降低风险。
除了ARCH模型，还有一种更广义的模型叫做GARCH模型，即广义自回归条件异方差模型。
GARCH模型在ARCH模型的基础上增加了过去时刻波动性的指数加权平均项。
这允许GARCH模型能够更好地捕捉到波动性的长期记忆特性。
GARCH模型的一般形式可以表示为：σ_t^2=α_0+α_1*ε_(t-1)^2+α_2*ε_(t-2)^2+...+α_p*ε_(t-p)^2+β_1*σ_(t-1)^2+β_2*σ_(t-2)^2+...+β_q*σ_(t-q)^2其中，σ_t^2表示在t时刻的波动性，α_0表示常数项，α_1,α_2,...,α_p是ARCH模型的参数，β_1,β_2,...,β_q是GARCH 模型的参数，ε_t-1,ε_t-2,...,ε_t-p是t时刻的残差，σ_t-1,σ_t-2,...,σ_t-q是t时刻的波动性。
GARCH模型在金融领域的应用更为广泛，因为它可以更准确地描述金融市场中的波动性。
ARCH模型与GARCH类模型实验报告
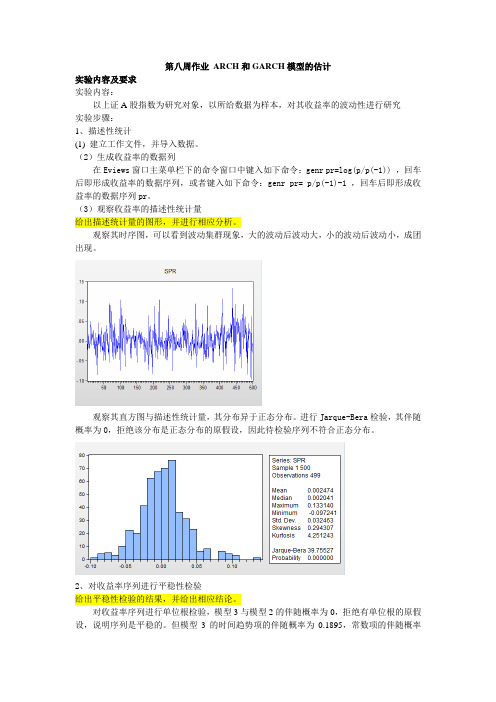
第八周作业ARCH和GARCH模型的估计实验内容及要求实验内容：以上证A股指数为研究对象，以所给数据为样本，对其收益率的波动性进行研究实验步骤：1、描述性统计(1) 建立工作文件，并导入数据。
（2）生成收益率的数据列在Eviews窗口主菜单栏下的命令窗口中键入如下命令：genr pr=log(p/p(-1)) ，回车后即形成收益率的数据序列，或者键入如下命令：genr pr= p/p(-1)-1 ，回车后即形成收益率的数据序列pr。
（3）观察收益率的描述性统计量给出描述统计量的图形，并进行相应分析。
观察其时序图，可以看到波动集群现象，大的波动后波动大，小的波动后波动小，成团出现。
观察其直方图与描述性统计量，其分布异于正态分布。
进行Jarque-Bera检验，其伴随概率为0，拒绝该分布是正态分布的原假设，因此待检验序列不符合正态分布。
2、对收益率序列进行平稳性检验给出平稳性检验的结果，并给出相应结论。
对收益率序列进行单位根检验，模型3与模型2的伴随概率为0，拒绝有单位根的原假设，说明序列是平稳的。
但模型3的时间趋势项的伴随概率为0.1895，常数项的伴随概率0.7314，在显著性水平0.05情况下不显著，故不选用。
而模型2的常数项的伴随概率为0.1121，也不显著，不选用。
因此模型1是最合适的模型，不含有常数项和时间趋势项。
3、均值方程的确定（1）观察收益率的自相关函数图，确定其均值方程的形式。
自相关图数值较小，比较难判断阶数，因此从AR（1）模型开始分析。
（2）对收益率做自回归给均值方程回归的结果AR（1）：该模型各项显著，故对其进行残差项白噪声检验，观察Q检验及其伴随概率，在显著性水平为0.05时，接受没有自相关性的原假设，是白噪声序列，可以选用。
4.ARCH效应的检验（1）用Ljung-Box Q 统计量对均值方程拟和后的残差及残差平方做自相关检验：给出检验结果，并作相应结论。
观察残差平方的自相关性，从伴随概率可见，其有很强的自相关性，说明存在ARCH效应。
金融计量学,唐勇,课件
原假设：序列不存在p阶自相关；备择假设：序列存在p阶自相关。 如果各阶Q统计量都没有超过设定的显著水平的临界值，则接受原假设。 超过临界值，就说明序列存在自相关。
yt xt ut , ut ~ N (0, t2 )
（7.3） （7.4）
t2 Var( yt It 1 ) 0 1ut 12 2ut 22 put p 2
这里要求
0 0, j 0
( j 1, , p) ，
• 注意：在ARCH（p）模型中，我们仍然假设扰动项不存在序列相关性， 还假设扰动项的无条件期望和条件期望都为0， 下面证明ARCH模型的性 质会用到。
u
2 序列指定的滞后阶数的自相关系 t
数（AC）和偏相关系数（PAC）（如本章第一节表7-3和表7-5所示）并且 计算出了相应阶数的Ljung-Box Q统计量：
QL, B T (T 2)
j 1
p
rj2 Tj
(7.20)
其中, 阶数。
r j 是残差系类的j 阶自相关系数，T为样本容量，p是设定的滞后
max( p , q )
i 1
(i i )ut2i vt j vt j
j 1
q
（7.10）
p， i 0 ，对 i q
，i 0 ，可以得到： （7.11）
ut2 0 [ ( L) ( L)]ut2 [1 ( L)]vt
s 1
（7.17）
1.ARCH-LM检验
LM 定的显著性水平 下 ，
2 R 其中，T表示样本的容量， 表示回归方程（7.17）的可决系数，在给
2
2 ( p ) LM ，接受原假设， ( p) ，拒绝 原假设。或者可以用 p值来判断，p 则拒绝原假设，否则接受原假设。
GARCH模型族
种说法是错误的。正确的说法是“分布的尾部越厚，峰度
值越大”。
K 1 T ( yt y )4
T
s
t 1
300
Series: SER01
250
Sample 1 10000 Observations 1105
200
Mean
0.410999
Median
4.080890
150
Maximum
63.56283
Skewness
0.650826
100
Kurtosis
42.38336
50 Jarque-Bera 646976.3
Probability 0.000000
0
-40 -20
0
20
40
60
高峰厚尾分布
-40 -20
0
20
40
60
低峰厚尾分布
Series: SER01 Sample 1 10000 Observations 1105
9.1 问题的提出
这种序列的特征是 （1）过程的方差不仅随时间变化，而且有时变化得很激烈。 （2）按时间观察，表现出“波动集群”（volatility clustering）特征，即方差在一 定时段中比较小，而在另一时段中比较大。 （3）从取值的分布看表现的则是“高峰厚尾”（leptokurtosis and fat-tail）特征， 即均值附近与尾区的概率值比正态分布大，而其余区域的概率比正态分布小。
6 4 D(JPY) (1995-2000)
高峰厚尾分布曲线
2
0
-2
正态分布曲线 -4
-6
-8 200 400 600 800 1000 1200 1400
第7章、ARCH模型和GARCH模型
精品文档第7章、ARCH模型和GARCH模型研究内容：研究随时间而变化的风险。
（回忆：Markowitz均值－方差投资组合选择模型怎样度量资产的风险）随意编辑精品文档本章模型与以前所学的异方差的不同之处：随机扰动项的无条件方差虽然是常数，但是条件方差是按规律变动的量。
波动率的聚类性（volatility clustering）：一段时间内，随机扰动项的波动的幅度较大，而另外一定时间内，波动的幅度较小。
如图，随意编辑精品文档0.80.60.40.20.0-0.2500100015002000随意编辑精品文档随意编辑精品文档随意编辑§1、ARCH 模型1、条件方差多元线性回归模型：t t t y X βε=+条件方差或者波动率（Condition variance ，volatility ）定义为精品文档随意编辑211var ()var(|)t t t t t σεεψ--≡=其中1t ψ-是信息集。
精品文档随意编辑2、ARCH 模型的定义Engle （1982）提出ARCH 模型（autoregressive conditional heteroskedasticity ，自回归条件异方差）。
ARCH(q)模型：t t t y βε=+x （1）t ε的无条件方差是常数，但是其条件分布为21|(0,)t t t N εψσ-:精品文档随意编辑22211t t q t q σωαεαε--=+++L （2） 其中1t ψ-是信息集。
方程（1）是均值方程（mean equation ）✓ 2t σ：条件方差，含义是基于过去信息的一期预测方差方程（2）是条件方差方程（conditional variance equation ），由二项组成精品文档随意编辑✓ 常数ω✓ ARCH 项2t i ε-：滞后的残差平方习题： 方程（2）给出了t ε的条件方差，请计算t ε的无条件方差。
精品文档随意编辑证明：利用方差分解公式：Var(X) = Var Y [E(X|Y)] + E Y [Var(X|Y)]由于21|(0,)t t t N εψσ-:，所以条件均值为0，条件方差为2t σ。
《ARCH和GARCH估计》课件
3 模型诊断和优化
解释如何对ARCH和GARCH模型进行诊断分析，以及优化模型的方法。
模型实证分析
数据分析
利用金融数据进行ARCH和 GARCH模型的实证分析，展示不 同模型的效果。
模型验证
介绍如何验证ARCH和GARCH模 型的准确性和可靠性，并对比实 证结果。
时间序列预测
探讨ARCH和GARCH模型在金融 时间序列预测中的应用，展示其 预测能力。
介绍GARCH模型的基本原理，并分析其在金融领域中的优势和局限性。
3 条件异方差性
解释条件异方差性的概念，为后续模型引入提供理论基础。
估计ARCH和GARCH模型的方法
1
最大似然估计法(MLE)
详细介绍最大似然估计法在ARCH和
广义矩法(GMM)
2
GARCH模型中的应用，并讨论其优缺点。
讲解广义矩法在ARCH和GARCH模型中的
展望未来，分析ARCH和GARCH模型的发展趋势，探讨可能的改进方向和研 究方向。
风险敞口计算
讲解如何使用ARCH和 GARCH模型计算个体资产或 投资组合的风险敞口。
ARCH和GARCH模型优劣势比较
1 ARCH模型的局限性和改进方法
探讨ARCH模型在应用上的局限性，并介绍改进方法和相关研究。
2 GARCH模型的局限性和改进方法
分析GARCH模型的局限性，并介绍改进方法以提高模型的准确性。
《ARCH和GARCH估计》 PPT课件
本课件将深入介绍ARCH和GARCH模型的估计方法和应用场景，帮助您更好 地分析金融资产价格波动，并在市场风险管理和投资组合风险管理方面提供 实用工具。
ARCH和GARCH模型简介
1 ARCH模型
解释如何对ARCH和GARCH模型进行诊断分析，以及优化模型的方法。
模型实证分析
数据分析
利用金融数据进行ARCH和 GARCH模型的实证分析，展示不 同模型的效果。
模型验证
介绍如何验证ARCH和GARCH模 型的准确性和可靠性，并对比实 证结果。
时间序列预测
探讨ARCH和GARCH模型在金融 时间序列预测中的应用，展示其 预测能力。
介绍GARCH模型的基本原理，并分析其在金融领域中的优势和局限性。
3 条件异方差性
解释条件异方差性的概念，为后续模型引入提供理论基础。
估计ARCH和GARCH模型的方法
1
最大似然估计法(MLE)
详细介绍最大似然估计法在ARCH和
广义矩法(GMM)
2
GARCH模型中的应用，并讨论其优缺点。
讲解广义矩法在ARCH和GARCH模型中的
展望未来，分析ARCH和GARCH模型的发展趋势，探讨可能的改进方向和研 究方向。
风险敞口计算
讲解如何使用ARCH和 GARCH模型计算个体资产或 投资组合的风险敞口。
ARCH和GARCH模型优劣势比较
1 ARCH模型的局限性和改进方法
探讨ARCH模型在应用上的局限性，并介绍改进方法和相关研究。
2 GARCH模型的局限性和改进方法
分析GARCH模型的局限性，并介绍改进方法以提高模型的准确性。
《ARCH和GARCH估计》 PPT课件
本课件将深入介绍ARCH和GARCH模型的估计方法和应用场景，帮助您更好 地分析金融资产价格波动，并在市场风险管理和投资组合风险管理方面提供 实用工具。
ARCH和GARCH模型简介
1 ARCH模型
ARCH模型和GARCH模型
ARCH模型和GARCH模型研究内容：研究随时间而变化的风险。
（回忆：Markowitz均值－方差投资组合选择模型怎样度量资产的风险）本章模型与以前所学的异方差的不同之处：随机扰动项的无条件方差虽然是常数，但是条件方差是按规律变动的量。
波动率的聚类性（volatility clustering）：一段时间内，随机扰动项的波动的幅度较大，而另外一定时间内，波动的幅度较小。
如图，0.80.60.40.20.0-0.2500100015002000§1、ARCH 模型1、条件方差多元线性回归模型：t t t y X βε=+条件方差或者波动率（Condition variance ，volatility ）定义为211var ()var(|)t t t t t σεεψ--≡=其中1t ψ-是信息集。
2、ARCH 模型的定义Engle （1982）提出ARCH 模型（autoregressive conditional heteroskedasticity ，自回归条件异方差）。
ARCH(q)模型：t t t y βε=+x （1）t ε的无条件方差是常数，但是其条件分布为21|(0,)t t t N εψσ-22211t t q t q σωαεαε--=+++ （2）其中1t ψ-是信息集。
方程（1）是均值方程（mean equation ）✓ 2t σ：条件方差，含义是基于过去信息的一期预测方差方程（2）是条件方差方程（conditional variance equation ），由二项组成 ✓ 常数ω✓ ARCH 项2t i ε-：滞后的残差平方习题： 方程（2）给出了t ε的条件方差，请计算t ε的无条件方差。
证明：利用方差分解公式：Var(X) = Var Y [E(X|Y)] + E Y [Var(X|Y)]由于21|(0,)t t t N εψσ-，所以条件均值为0，条件方差为2t σ。
ARCH与GARCH模型
ARCH 与GARCH 模型1. 自回归条件异方差模型3.1.1问题的提出对异方差误差分布的修正能够导致更加有效的参数估计。
比如在回归方程εβββttttx x y +++=33221（3.1.1）中的εt的方差可能与xt22成正比，在这种情况下，我们能够使用加权最小二乘法，即令方程的两边同时除以变量xt2，然后用普通最小二乘法估计变化后的回归方程εβββ*23322121ttttttxx x x y +++= （3.1.2）在有些应用场合下，能够认为误差项是随时间变化的同时依靠于过去的误差大小。
通货膨胀与股票市场收益都属于这种情形。
在这些实际应用中，常常有大的误差与小的误差成群出现的情形，换句话说，存在着一种特殊的异方差形式，回归误差的方差依靠于过去不久误差的变化程度。
一个被广泛使用以解决这类异方差模型是由Robert Engle 研究进展出来的，他认为用一个自回归条件异方差模型（Autoregressive conditional heteroscedasticity model ，简计为ARCH 模型）会提高有效性。
3.1.2定义通常的，公式（1）中随机误差项t ε的方差2t σ能够依靠于任意多个滞后变化量it -ε（i=1,2,…p ），记作ARCH （p ）εαεαεαασ222221102.......p t p t t t---++++= （3.1.3）注意：（1） 为了保证在给定i t -2ε条件下，02≥t σ，就务必要求0≥α（p ,,1,0 =α）； （2） 要保证误差序列t ε的平稳性，系数务必满足：121 p ααα++。
3.1.3检验3.1.3.1Breusch-Pagan 检验 在同方差的假设下条件下：SSR/2~X 2(1)根据Eviews3.1 OLS 处理结果，可根据下式计算检验的统计量SSR/2SSESSR SSRSST SSR R +==2 查自由度为1时的2χ分布表，找出给定显著性水平α条件下临界值，比较检验统计量与临界值的大小，以确定同意还是拒绝模型同方差的零假设3.1.3.2拉格朗日乘子检验法（ＬＭ）已经讨论过两种假设检验法：F 检验（Wald 检验）法(第5章)与似然比检验法。
向量自回归与ARCH、GARCH模型剖析
向量自回归预测是计量经济分析的重要部分，宽泛的说，依据时间序列数据进行经济预测的方法有五种：（1）指数平滑法；（2）单一方程回归模型；（3）联立方程回归模型；（4）单整自回归移动平均模型；（5）向量自回归模型（V AR ，vector autoregression ）。
一、V AR 的估计V AR 方法论同时考虑几个内生变量，它看起来类似于联立方程模型。
但是，在V AR 模型中，每一个内生变量都是由它的滞后或过去值以及模型中所有其他内生变量的滞后或过去值来解释。
通常模型中没有任何外生变量。
在联立方程模型中，我们把一些变量看作内生的，而另一些变量看作外生的或预定的，在估计这些模型之前，必须肯定方程组中的方程是可识别的，而为达到识别的目的，常常要假定某些预定变量仅出现在某些方程之中，这些决定往往是主观的，因此这种方法受到C.A.西姆斯（Christopher Sims ）的严厉批评，他认为如果在一组变量中有真实的联立性，这些变量就应该平等对待，而不应事先区分内生和外生变量，以此思路，其推出了V AR 模型。
例我们想考虑中国的货币（M1）与利率（R ）的关系。
如果通过格兰杰因果关系检验，我们无法拒绝两者之间有双向因果关系的假设，即M1 影响R ，而R 反过来又影响M1，这种情形是应用V AR 的理想情形。
假定每个方程都含有M1 和R 的k 个滞后值作为回归元，每个方程都可以用OLS 去估计，实际模型如下： 11111k kt j t j j t j t j j M M R u αβγ--===+++∑∑2111k kt j t j j t j t j j R M R u αθλ--=='=+++∑∑ 其中u 是随机误差项，在V AR 术语中称为脉冲值（impulses ）。
在估计以上方程时，必须先决定最大滞后长度，这是一个经验问题，包括过多的滞后项将消耗自由度，而且会引入多重共线性的可能性，而包含过少的滞后值将导致设定误差，解决这个问题的方法之一就是使用赤池、施瓦茨或汉南—奎因准则中的某一个准则，并选择准则最低值的模型，因此，这个过程中试错法就不可避免。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第7章、ARCH模型和GARCH模型研究内容：研究随时间而变化的风险。
（回忆：Markowitz均值－方差投资组合选择模型怎样度量资产的风险）本章模型与以前所学的异方差的不同之处：随机扰动项的无条件方差虽然是常数，但是条件方差是按规律变动的量。
波动率的聚类性（volatility clustering）：一段时间内，随机扰动项的波动的幅度较大，而另外一定时间内，波动的幅度较小。
如图，0.8 0.6 0.4 0.2 0.0 -0.2§1、ARCH 模型1、条件方差多元线性回归模型：t t t y X βε=+条件方差或者波动率（Condition variance ，volatility ）定义为211var ()var(|)t t t t t σεεψ--≡=其中1t ψ-是信息集。
2、ARCH 模型的定义Engle （1982）提出ARCH 模型（autoregressive conditional heteroskedasticity ，自回归条件异方差）。
ARCH(q)模型：t t t y βε=+x （1）t ε的无条件方差是常数，但是其条件分布为21|(0,)t t t N εψσ-:22211t t q t q σωαεαε--=+++L （2）其中1t ψ-是信息集。
方程（1）是均值方程（mean equation ）✓ 2t σ：条件方差，含义是基于过去信息的一期预测方差方程（2）是条件方差方程（conditional variance equation ），由二项组成 ✓ 常数ω✓ ARCH 项2t i ε-：滞后的残差平方习题： 方程（2）给出了t ε的条件方差，请计算t ε的无条件方差。
证明：利用方差分解公式：Var(X) = Var Y [E(X|Y)] + E Y [Var(X|Y)]由于21|(0,)t t t N εψσ-:，所以条件均值为0，条件方差为2t σ。
那么，21var ()t t t σε-=2122112211var()[var ()] () t t t t t q t q t q t qE E E E E εεσωαεαεωαεαε-----===+++=+++L L 推出1var()1t qωεαα=---L ，说明1(0,)1t qN ωεαα---:L3、ARCH 模型的平稳性条件在ARCH(1)模型中，观察参数α的含义： 当1α→时，var()t ε→∞当0α→时，退化为传统情形，(0,)t N εω:ARCH 模型的平稳性条件：1i α∑<（这样才得到有限的方差）4、ARCH 效应检验ARCH LM Test ：拉格朗日乘数检验 建立辅助回归方程222011t t q t q t e e e v ααα--=++++L此处e 是回归残差。
原假设：H0：序列不存在ARCH 效应即H0：120q ααα====L可以证明：若H 0为真，则22LM ()mR q χ=:此处，m 为辅助回归方程的样本个数。
R 2为辅助回归方程的确定系数。
Eviews操作：①先实施多元线性回归②view/residual/Tests/ARCH LM Test§2、GARCH模型的实证分析从收盘价，得到收益率数据序列。
series r=log(p)-log(p(-1))点击序列p，然后view/line graph2000150010005005001000150020000.8 0.6 0.4 0.2 0.0 -0.21、检验是否有ARCH现象。
首先回归。
取2000到2254的样本。
输入ls r c，得到0.080.040.00-0.04-0.08-0.12200020502100215022002250Dependent Variable: RMethod: Least SquaresDate: 10/21/04 Time: 21:26Sample: 2000 2254Included observations: 255Variable Coefficient Std. Error t-Statistic Prob.C 0.000432 0.001087 0.397130 0.6916Adjusted R-squared 0.000000 S.D. dependent var 0.017364 S.E. of regression 0.017364 Akaike info criterion -5.264978 Sum squared resid 0.076579 Schwarz criterion -5.251091 Log likelihood 672.2847 Durbin-Watson stat 2.049819 问题：这样进行回归的含义是什么？其次，view/residual tests/ARCH LM test，得到ARCH Test:Obs*R-squared 44.68954 Probability 0.000002 Test Equation:Dependent Variable: RESID^2Method: Least SquaresDate: 10/21/04 Time: 21:27Sample(adjusted): 2010 2254Included observations: 245 after adjusting endpointsVariable Coefficient Std. Error t-Statistic Prob.RESID^2(-1) 0.141549 0.065237 2.169776 0.0310 RESID^2(-2) 0.055013 0.065823 0.835766 0.4041 RESID^2(-3) 0.337788 0.065568 5.151697 0.0000 RESID^2(-4) 0.026143 0.069180 0.377893 0.7059 RESID^2(-5) -0.041104 0.069052 -0.595260 0.5522 RESID^2(-6) -0.069388 0.069053 -1.004854 0.3160 RESID^2(-7) 0.005617 0.069178 0.081193 0.9354 RESID^2(-8) 0.102238 0.065545 1.559806 0.1202 RESID^2(-9) 0.011224 0.065785 0.170619 0.8647 RESID^2(-10) 0.064415 0.065157 0.988613 0.3239Adjusted R-squared 0.147466 S.D. dependent var 0.000679 S.E. of regression 0.000627 Akaike info criterion -11.86836 Sum squared resid 9.19E-05 Schwarz criterion -11.71116 Log likelihood 1464.875 F-statistic 5.220573 Durbin-Watson stat 2.004802 Prob(F-statistic) 0.0000012、模型定阶：如何确定q实施ARCH LM test时，取较大的q，观察滞后残差平方的t统计量的p－value即可。
此处选取q＝3。
因此，可以对残差建立ARCH(3)模型。
3、ARCH模型的参数估计参数估计采用最大似然估计。
具体方法在GARCH一节中讲解。
如何实施ARCH过程：由于存在ARCH效应，所以点击estimate，在method中选取ARCH得到如下结果Dependent Variable: RMethod: ML - ARCHDate: 10/21/04 Time: 21:48Sample: 2000 2254Included observations: 255Convergence achieved after 13 iterationsCoefficient Std. Error z-Statistic Prob.C -0.000640 0.000750 -0.852888 0.3937Variance EquationARCH(1) 0.244793 0.082640 2.962142 0.0031 ARCH(2) 0.081425 0.077428 1.051624 0.2930 ARCH(3) 0.457883 0.109698 4.174043 0.0000 Adjusted R-squared -0.019884 S.D. dependent var 0.017364 S.E. of regression 0.017535 Akaike info criterion -5.495982 Sum squared resid 0.076872 Schwarz criterion -5.426545 Log likelihood 705.7377 Durbin-Watson stat 2.042013为了比较，观察将q放大对系数估计的影响Dependent Variable: RMethod: ML - ARCHDate: 10/21/04 Time: 21:54Sample: 2000 2254Included observations: 255Convergence achieved after 16 iterationsCoefficient Std. Error z-Statistic Prob.C -0.000601 0.000751 -0.799909 0.4238Variance EquationARCH(1) 0.262009 0.090256 2.902959 0.0037ARCH(2) 0.041930 0.070518 0.594596 0.5521ARCH(3) 0.452187 0.108488 4.168076 0.0000ARCH(4) -0.021920 0.050982 -0.429956 0.6672ARCH(5) 0.037620 0.044394 0.847408 0.3968 Adjusted R-squared -0.027830 S.D. dependent var 0.017364 S.E. of regression 0.017603 Akaike info criterion -5.483292 Sum squared resid 0.076851 Schwarz criterion -5.386081Log likelihood 706.1198 Durbin-Watson stat 2.042568 观察：说明q选取为3确实比较恰当。