行星齿轮变速箱的结构参数与传动比计算

行星齿轮减速器的相关计算行星齿轮减速器是一种常用的机械传动装置，其特点是结构紧凑、承载能力大、传动效率高。

在工程设计和机械计算中，对行星齿轮减速器的相关参数进行计算是必不可少的工作。

本文将详细介绍行星齿轮减速器的相关计算方法。

一、行星齿轮减速器的基本构造二、行星齿轮减速器的传动比计算传动比是指输入轴和输出轴的转速比，可以通过以下公式计算：i=(N_s+N_r)/N_s其中，i为传动比，N_s为太阳齿轮的齿数，N_r为行星齿轮的齿数。

行星齿轮减速器的传动比可以通过调整太阳齿轮和行星齿轮的齿数来实现。

三、行星齿轮减速器的传动效率计算η=(1-δ/100)*(1-ε/100)其中，η为传动效率，δ为齿间损失系数，ε为噪声损失系数。

行星齿轮减速器的传动效率受到齿轮的磨损和摩擦影响，一般情况下，传动效率在95%以上。

四、行星齿轮减速器的扭矩计算输入轴扭矩计算可以通过以下公式计算：T_in = P / (n * η)其中，T_in为输入轴扭矩，P为输出功率，n为输入轴转速，η为传动效率。

输出轴扭矩计算可以通过以下公式计算：T_out = i * T_in其中，T_out为输出轴扭矩，i为传动比，T_in为输入轴扭矩。

五、行星齿轮减速器的选择在实际工程中，选择合适的行星齿轮减速器需要考虑以下因素：1.承载能力：根据实际应用需求，选择承载能力适当的行星齿轮减速器。

2.传动比：根据需要的输出转速和输入转速，选择合适的行星齿轮减速器。

3.外形尺寸：根据实际安装空间，选择符合尺寸要求的行星齿轮减速器。

4.传动效率：选择传动效率高的行星齿轮减速器，以提高传动效率和节能效果。

5.稳定性：选择结构稳定、运行平稳的行星齿轮减速器，以减少振动和噪声。

六、行星齿轮减速器的基本计算流程1.确定输入功率、输入转速和输出转速。

2.根据输入功率和输入转速计算输入轴扭矩。

3.根据输入轴扭矩和传动比计算输出轴扭矩。

4.根据输出轴扭矩和输出转速计算输出功率。

行星齿轮传动比计算公式【最新版】目录1.行星齿轮传动比计算公式的概述2.行星齿轮传动比的计算方法3.行星齿轮传动比的特点4.应用行星齿轮传动比的注意事项正文行星齿轮传动比计算公式是一种在机械传动领域中常用的计算方式，它可以帮助我们准确地计算出行星齿轮传动系统中的传动比。

行星齿轮传动比计算公式的概述如下：行星齿轮传动比是指主动轮（太阳轮）的角速度与从动轮（行星轮）的角速度之比。

在行星齿轮传动系统中，太阳轮通过行星轮向外界输出动力，因此，行星齿轮传动比的计算至关重要。

它可以帮助我们了解传动系统的工作状态，以及调整传动系统中的参数，以达到最佳的工作效果。

行星齿轮传动比的计算方法如下：假设太阳轮的齿数为 Z1，行星轮的齿数为 Z2，太阳轮的角速度为ω1，行星轮的角速度为ω2。

那么，行星齿轮传动比计算公式可以表示为：传动比 = ω1 / ω2 = Z1 / Z2在实际应用中，行星齿轮传动比通常是瞬时传动比，即太阳轮和行星轮的瞬时角速度比。

但是，在某些特殊情况下，例如当太阳轮和行星轮的转速相同时，瞬时传动比就会变为恒定的平均传动比。

行星齿轮传动比具有以下特点：1.行星齿轮传动比是瞬时传动比，即随太阳轮和行星轮的角速度变化而变化。

2.行星齿轮传动比的计算方法简单，只需要知道太阳轮和行星轮的齿数和角速度即可。

3.行星齿轮传动比可以帮助我们了解传动系统的工作状态，以及调整传动系统中的参数，以达到最佳的工作效果。

应用行星齿轮传动比时，需要注意以下事项：1.确保行星齿轮传动比的计算准确无误，以免影响传动系统的工作效果。

2.根据行星齿轮传动比的计算结果，及时调整传动系统中的参数，以达到最佳的工作效果。

3.注意行星齿轮传动比的变化规律，以便在传动系统出现异常时，及时进行处理。

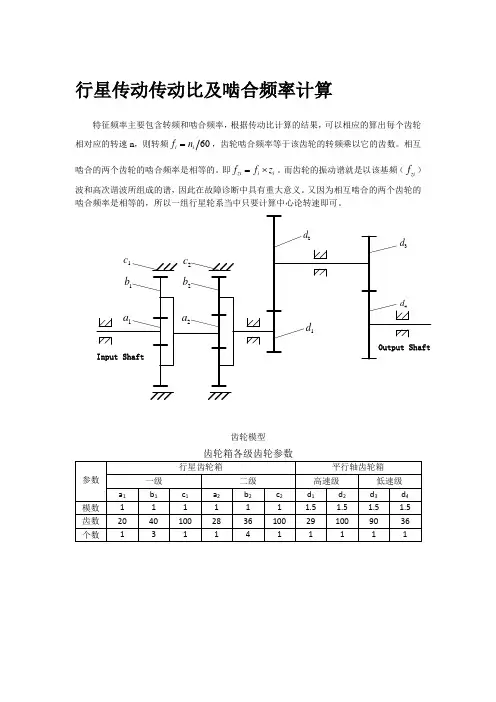
行星传动传动比及啮合频率计算特征频率主要包含转频和啮合频率，根据传动比计算的结果，可以相应的算出每个齿轮相对应的转速n ，则转频60i i f n =，齿轮啮合频率等于该齿轮的转频乘以它的齿数。

相互啮合的两个齿轮的啮合频率是相等的。

即zi i i f f z =⨯。

而齿轮的振动谱就是以该基频（zi f ）波和高次谐波所组成的谱，因此在故障诊断中具有重大意义。

又因为相互啮合的两个齿轮的啮合频率是相等的，所以一组行星轮系当中只要计算中心论转速即可。

1a 1b 1c 2a 2b 2c Input ShaftOutput Shaft2d 1d 3d 4d齿轮模型n –输入转速；Za1–第一级太阳轮齿数；Zb1 –第一级行星轮齿数；Zc1–第一级内齿圈齿数； Za2 –第二级太阳轮齿数；Zb2 –第二级行星轮齿数；Zc2 –第二级内齿圈齿数；（1） 一级行星轮系：111111a H c c H a n n z n n z -=-- 其中，n n n a c ==11,0 ，则 )1//(11111+==a c a Hb z z n n n =n 61（2） 二级行星轮系：222222a H c c H a n n zn n z -=--其中，122,0H a c n n n ==，则)1//(22222+==a c a H b z z n n n =2327a n 行星轮系级: 传动比i =192/7 （3）平行轴：中间低速级： 传动比i1= 小大n n =100/29高速级： 传动比i2= 小大n n =2.5 平行轴传动比：i=8.6 总传动比：i=232齿轮箱振动特征频率 1. 啮合频率:1）转速同步频率 n f = n/60 式中，n 为轴转速（转/分）。

2）定轴齿轮啮合频率n f = nz/60 式中，n 为轴转速（转/分）， r z 为齿轮齿数。

3）行星轮系，啮合频率用下式计算： m f = a b a c b z f f z f ⨯-=⨯)( 式中，b n 为行星轮架转速（转/分），c z 为内齿圈齿数，a f 为太阳轮转频，a z 为太阳轮齿数。

行星齿轮机构的设计与计算行星齿轮机构是一种广泛应用于机械传动系统中的重要装置，其可以实现高速度、高传动比和高扭矩的传动效果，被广泛应用于工业领域。

本文将从行星齿轮机构的结构设计、传动计算和性能评价三个方面，对其进行详细叙述。

一、行星齿轮机构的结构设计行星齿轮机构包括太阳轮、行星轮、内齿圈和行星架等组成。

在进行结构设计时，需要根据传动比、扭矩和转速等要求，选取合适的节数及行星齿轮的参数，并确定合适的齿轮副布置。

在选择节数时，应根据所需的传动比和运动稳定性等因素进行综合考虑。

齿轮副布置可以选择封闭式和开放式两种形式，封闭式结构更为紧凑，但加工和安装难度较大。

而开放式结构则相对较为简洁，方便维护和安装。

二、行星齿轮机构的传动计算1.传动比计算传动比=（Zs+Zr）/Zs其中，Zs表示太阳齿轮的齿数，Zr表示行星轮的齿数。

2.齿轮尺寸计算齿轮尺寸计算主要包括齿轮副模数的选择和齿面强度的计算。

在选择齿轮副模数时，需要根据预计的工作载荷和制造工艺等因素进行综合考虑。

齿面强度的计算可以通过以下公式求解：齿面强度Ft=KF*KH*m*b*Y其中，KF为荷载系数，KH为接触系数，m为模数，b为齿轮宽度，Y 为齿轮材料影响系数。

三、行星齿轮机构的性能评价1.传动误差传动误差是指传动中实际传动比与理论传动比之间的差异。

传动误差主要由机构的制造误差和装配误差引起。

为了降低传动误差，可以采用精密加工和装配工艺，优化齿轮表面处理等措施。

2.传动效率传动效率是指输入功率与输出功率之间的比值，可以通过以下公式计算：传动效率η=（输出功率/输入功率）*100%传动效率的高低主要取决于齿轮的摩擦损失和变形损失。

为了提高传动效率，可以采用高精度的齿轮和适当的润滑措施。

3.寿命综上所述，行星齿轮机构的设计与计算需要根据传动要求对结构进行设计，并进行传动比和齿轮尺寸的计算。

在性能评价方面，需要关注传动误差、传动效率和寿命等因素，并采取相应的措施进行优化。

行星齿轮机构传动比计算方法Key words: epicyclic gear train; speed ratio; compute way.随着行星齿轮减速器以及行星齿轮传动在变速箱中的广泛应用，对行星齿轮传动的了解和掌握已成为工程技术人员的必要技能。

但是，对于刚接触行星齿轮传动的工程技术人员来说，行星齿轮传动的速比计算比较不容易理解和掌握。

本文通过对各类参考资料及教科书中的行星齿轮传动速比计算方法进行总结归纳，并针对常用的最具代表性的2K-H型行星齿轮传动，分别用不同方法对其传动特性方程进行了推导论证。

行星齿轮传动或称周转轮系。

根据《机械原理》[1]上的定义，我们可把周转轮系分为差动轮系和行星轮系。

为理解方便，本论文所讨论限于2K-H型周转轮系。

关于行星齿轮传动（周转轮系）的速比计算方法，归纳起来有两大类四种方法，分别为由行星架固定法和力矩法组成的分析法；由速度图解法和矢量法组成的图解法[2]。

矢量图解法一般适用于圆锥齿轮组成的行星齿轮传动，在此不作介绍；下面分别运用其它三种计算方法对2K-H型周转轮系的传动特性方程（1）进行推导。

1－太阳轮 2－行星轮 3－内齿圈 H －行星架 图1 行星齿轮传动Fig 1 Epicyclic gear train0)1(31=++-αωωαωH （1） 结合图1，式中1ω为太阳轮1的转速、Hω为行星架H 转速、3ω为内齿圈3转速、α为内齿圈3与太阳轮1的齿数比即13Z Z =α。

1 行星架固定法机械专业教科书上一般介绍的都是此种方法，也可叫转化机构法。

其理论是一位名叫Wlies 的科学家于1841年提出的，即“一个机构整体的绝对运动并不影响其内部各构件间的相对运动” [3]，就像手表的时针、分针、秒针的相对运动不会因带表人的行动而变化。

如图2所示，其中太阳轮1、行星轮2、内齿圈3、行星架H 的转速分别为Hωωωω、、、321。

我们假定整个行星轮系放在一个绕支点O 旋转的圆盘上，此圆盘的转速为 H ω-。

行星轮系传动比的计算
回忆上节内容:定轴轮系传动比的计算公式为:i1k=n1/nk=i1*i2*i3* (i)
定轴轮系的特点是:每个齿轮都是围绕固定的周线旋转,没有自身的公转.
今天我们看以下行星轮系,请同学们思考:行星的运动特点?
对,行星一方面不仅围绕固定的轴线旋转,而且会围绕太阳公转.
下面这张图就是行星轮系,结构和特点我们看一下:
结构:齿圈,太阳轮,行星轮,行星齿轮架
原理:行星齿轮不仅自转,还有围绕太阳轮的公转.
计算传动比:转化法:化行星轮系为定轴轮系
简化结构如下:
太阳轮:n1 z1
行星轮:n2 z2
齿圈:n3 z3
行星架:nh Zh
则传动比计算公式为:ng-nh/nk-nh=(-1)m齿轮G,K之间所有从动轮齿数的连乘积/齿轮G,K之间所有主动轮齿数的连乘积
例题:如图所示为圆锥齿轮组成的差动轮系,Z1=Z2=Z3,求齿轮1,3和行星架H三者转速的关系
解:该轮系为差动轮系,其中齿轮1,3及行星架H的轴线均互相平行或重合,将齿轮1看作主动轮,齿轮3看作从动轮,并设齿轮1的转向为正,通过画箭头,齿轮3的箭头与齿轮1 的相反,故为负,由公式计算:
N1-nh/n3-nh=-z2z3/z1z2=-z3/z1=-1
所以三者转速关系为:
2nh=n1+n3
分析:行星轮系在汽车上的应用:1.汽车后桥差速器
2.行星齿轮机构变速器。

行星齿轮传动比计算在《机械设计》上，行星齿轮求解是通过列一系列方程式求解，其求解过程繁琐容易出错，其实用不着如此，只要理解了传动比eab i 的含义，就可以很快地直接写出行星齿轮的传动比，其关键是掌握几个根据e ab i 的含义推导出来公式，随便多复杂的行星齿轮传动机构，根据这几个公式都能从头写到尾直接把其传动比写出来，而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。

一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1 a cxa bx abci i i = ―――――――――――――――――――――――――2 a cb abc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后，不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。

关键是要善于选择中间的一些部件作为参照，使其最后形成都是定轴传动，所以这些参照基本都是一些行星架等例如象论坛中“大模王”兄弟所举的例子：在此例中，要求出e ab i ＝？，如果行星架固定不动的话，这道题目就简单多了，就是一定轴传动。

所以我们要想办法把e ab i 变成一定轴传动，所以可以根据公式a cx a bx a bci i i =将x 加进去， 所以可以得出：e bx e ax eab i i i =要想变成定轴传动，就要把x 放到上面去，所以这里就要运用第一个公式1=+c ba abc i i 了，所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。

定轴传动的传动比就好办了，直接写出来就可以了。

即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构：已知其各轮的齿数为z 1=100，z 2=101，z 2’ =100 ，z 3=99。

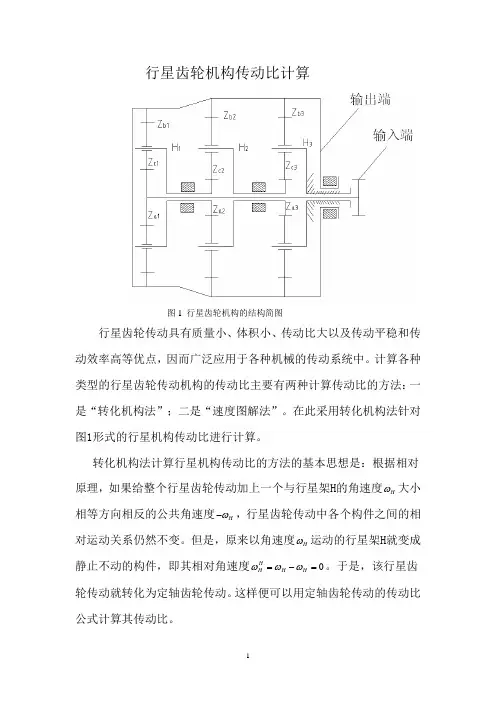
行星齿轮机构传动比计算图1 行星齿轮机构的结构简图行星齿轮传动具有质量小、体积小、传动比大以及传动平稳和传动效率高等优点，因而广泛应用于各种机械的传动系统中。

计算各种类型的行星齿轮传动机构的传动比主要有两种计算传动比的方法：一是“转化机构法”；二是“速度图解法”。

在此采用转化机构法针对图1形式的行星机构传动比进行计算。

转化机构法计算行星机构传动比的方法的基本思想是：根据相对原理，如果给整个行星齿轮传动加上一个与行星架H 的角速度H ω大小相等方向相反的公共角速度H ω-，行星齿轮传动中各个构件之间的相对运动关系仍然不变。

但是，原来以角速度H ω运动的行星架H 就变成静止不动的构件，即其相对角速度0HHH H ωωω=-=。

于是，该行星齿轮传动就转化为定轴齿轮传动。

这样便可以用定轴齿轮传动的传动比公式计算其传动比。

总传动比 1a bi ωω=，其中1a ω、b ω为主动件和被动件的角速度 根据该计算方法的基本思想，结合图1的具体结构，得到第一级传动比为：1111111a H b b H a zi z ωωωω-==-- (1)同理第二级和第三级传动比分别为：2222222a H b b H a zi z ωωωω-==-- (2)3333333a Hb b H a zi z ωωωω-==-- (3)根据图1中的实际结构，及三个内齿圈连接为一体，且第三级行星架H3固定，所以有123b b b b ωωωω===，30H ω= ， 12H a ωω= ，23H a ωω= （4） 由(3)式可得3333233b b a b b H a a z zz z ωωωω=-⨯=-⨯= (5) 把（5）式代入（2）式可得32223232223b a b a H a b b b H a b ba z z zz z z ωωωωωωωω+⨯-==--+⨯所以得23323321233233()[(1)]b b b b b b a b b b b H a a a a a a z z z z z zz z z z z z ωωωωωω=-⨯+⨯-⨯=-⨯⨯++= (6) 把（6）式代入（1）式可得：2331112331233111233[(1)][(1)]b b b a b a H a a a b b b b b H a b b a a a z z z z z z zz z z z z z z ωωωωωωωω+⨯⨯++-==--+⨯⨯++ (7)式（7）可化简为：123323323323312332331233233[(1)][(1)]1[(1)]1[(1)]a b b b b b b b a a a a a a b b b b b b b a a a a a a a z z z z z zi z z z z z z zz z zz z zz z z z z z z ωω+⨯+++⨯++==-+⨯+++⨯++ （8）由（8）式可得123323312332331[(1)][(1)]b b b b b b b a a a a a a a z z z z z z z i z z z z z z z ⎧⎫=-⨯+⨯++-⨯++⎨⎬⎩⎭11233233112332331233112331[(1)][(1)][(1)](1)b b b b b b b b a a a a a a a a b b b b b a a a a a z z z z z z z z z z z z z z z z z z z z z z z z z z =--⨯⨯++-⨯++=--⨯++⨯+所以12331123311(1)[(1)](1)b b b b b a a a a a z z z z z i z z z z z -=-+-⨯++⨯+ 12331233(1)[1(1)]b b b b a a a a z z z zz z z z =-+⨯+⨯++ 123123(1)(1)(1)b b b a a a z z z z z z =-+⨯+⨯+ 所以得总传动比1231231(1)(1)(1)b b b a a a z z zi z z z =-+⨯+⨯+ 即为该种行星结构的传动比。

行星传动比计算公式行星传动比计算可不是个简单的事儿，不过咱一步步来，保证让您搞清楚！先来说说啥是行星传动。

您就想象一下，有几个小齿轮像行星一样绕着一个大太阳（中心轮）转，这就是行星传动啦。

那这行星传动比到底咋算呢？咱们来看个例子。

比如说有一个行星齿轮系，中心轮的齿数是 20，行星轮的齿数是 10，内齿圈的齿数是 50。

这时候，咱就得用公式来算算啦。

行星传动比的计算公式是：i = 1+ Zr / Zs 。

这里的 Zr 是内齿圈的齿数，Zs 是太阳轮的齿数。

就拿刚才那个例子来说，内齿圈齿数 50，太阳轮齿数 20，那传动比 i 就等于 1 + 50 / 20 = 3.5 。

这就意味着输入转 3.5 圈，输出才转 1 圈。

记得有一次，我给学生们讲这个知识点。

有个小家伙特别可爱，瞪着大眼睛问我：“老师，这齿轮转来转去的，我头都晕啦，到底有啥用啊？”我笑着跟他说：“你想想看呀，咱们骑的自行车，要是没有合适的传动比，那骑起来得多费劲呀！还有汽车的变速箱，也是通过不同的传动比来让车在不同速度下都能跑得顺顺当当的。

”这小家伙一听，好像有点明白了，点着头说：“哦，原来是这样啊！”在实际应用中，行星传动比的计算可重要啦。

比如在一些大型机械里，要想让机器运转得高效、稳定，就得把传动比算得准准的。

要是算错了，那可就麻烦大了，说不定机器就“罢工”啦。

而且啊，不同的行星传动结构，计算方法还可能会有点小变化。

但不管怎么变，咱们抓住核心的公式和原理，就不怕搞不定。

所以说，这行星传动比的计算虽然有点复杂，但只要咱们多琢磨琢磨，多做做练习题，就一定能掌握好。

总之，搞清楚行星传动比的计算，对于机械设计、工程制造等等领域那可都是非常关键的。

希望您也能轻松拿下这个知识点，让它为您的知识宝库添砖加瓦！。

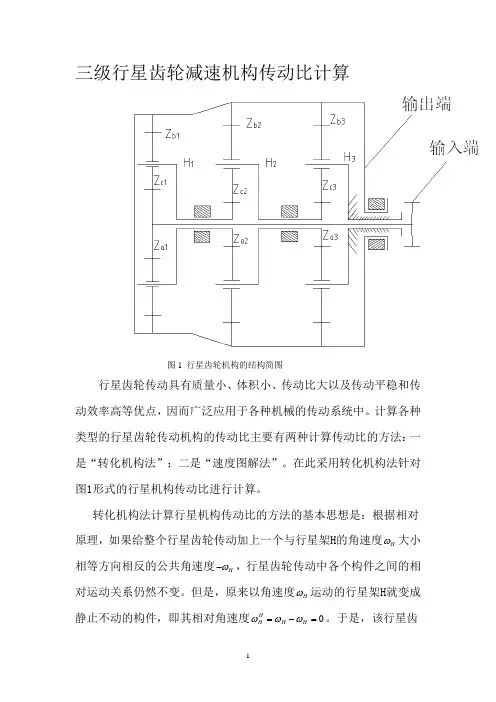
三级行星齿轮减速机构传动比计算图1 行星齿轮机构的结构简图行星齿轮传动具有质量小、体积小、传动比大以及传动平稳和传动效率高等优点，因而广泛应用于各种机械的传动系统中。

计算各种类型的行星齿轮传动机构的传动比主要有两种计算传动比的方法：一是“转化机构法”；二是“速度图解法”。

在此采用转化机构法针对图1形式的行星机构传动比进行计算。

转化机构法计算行星机构传动比的方法的基本思想是：根据相对原理，如果给整个行星齿轮传动加上一个与行星架H 的角速度H ω大小相等方向相反的公共角速度H ω-，行星齿轮传动中各个构件之间的相对运动关系仍然不变。

但是，原来以角速度H ω运动的行星架H 就变成静止不动的构件，即其相对角速度0HHH H ωωω=-=。

于是，该行星齿轮传动就转化为定轴齿轮传动。

这样便可以用定轴齿轮传动的传动比公式计算其传动比。

总传动比 1a bi ωω=，其中1a ω、b ω为主动件和被动件的角速度 根据该计算方法的基本思想，结合图1的具体结构，得到第一级传动比为：1111111a H b b H a zi z ωωωω-==-- (1)同理第二级和第三级传动比分别为：2222222a H b b H a zi z ωωωω-==-- (2)3333333a Hb b H a zi z ωωωω-==-- (3)根据图1中的实际结构，及三个内齿圈连接为一体，且第三级行星架H3固定，所以有123b b b b ωωωω===，30H ω= ， 12H a ωω= ，23H a ωω= （4） 由(3)式可得3333233b b a b b H a a z zz z ωωωω=-⨯=-⨯= (5) 把（5）式代入（2）式可得32223232223b a b a H a b b b H a b ba z z zz z z ωωωωωωωω+⨯-==--+⨯所以得23323321233233()[(1)]b b b b b b a b b b b H a a a a a a z z z z z zz z z z z z ωωωωωω=-⨯+⨯-⨯=-⨯⨯++= (6) 把（6）式代入（1）式可得：2331112331233111233[(1)][(1)]b b b a b a H a a a b b b b b H a b b a a a z z z z z z zz z z z z z z ωωωωωωωω+⨯⨯++-==--+⨯⨯++ (7)式（7）可化简为：123323323323312332331233233[(1)][(1)]1[(1)]1[(1)]a b b b b b b b a a a a a a b b b b b b b a a a a a a a z z z z z zi z z z z z z zz z zz z zz z z z z z z ωω+⨯+++⨯++==-+⨯+++⨯++ （8）由（8）式可得123323312332331[(1)][(1)]b b b b b b b a a a a a a a z z z z z z zi z z z z z z z ⎧⎫=-⨯+⨯++-⨯++⎨⎬⎩⎭11233233112332331233112331[(1)][(1)][(1)](1)b b b b b b b b a a a a a a a a b b b b b a a a a a z z z z z z z z z z z z z z z z z z z z z z z z z z =--⨯⨯++-⨯++=--⨯++⨯+所以12331123311(1)[(1)](1)b b b b b a a a a a z z z z z i z z z z z -=-+-⨯++⨯+ 12331233(1)[1(1)]b b b b a a a a z z z zz z z z =-+⨯+⨯++ 123123(1)(1)(1)b b b a a a z z z z z z =-+⨯+⨯+ 所以得总传动比1231231(1)(1)(1)b b b a a a z z zi z z z =-+⨯+⨯+ 即为该种行星结构的传动比。