行星传动比及啮合频率计算

行星齿轮传动比计算公式【最新版】目录1.行星齿轮传动比计算公式的概述2.行星齿轮传动比的计算方法3.行星齿轮传动比的特点4.应用行星齿轮传动比的注意事项正文行星齿轮传动比计算公式是一种在机械传动领域中常用的计算方式，它可以帮助我们准确地计算出行星齿轮传动系统中的传动比。

行星齿轮传动比计算公式的概述如下：行星齿轮传动比是指主动轮（太阳轮）的角速度与从动轮（行星轮）的角速度之比。

在行星齿轮传动系统中，太阳轮通过行星轮向外界输出动力，因此，行星齿轮传动比的计算至关重要。

它可以帮助我们了解传动系统的工作状态，以及调整传动系统中的参数，以达到最佳的工作效果。

行星齿轮传动比的计算方法如下：假设太阳轮的齿数为 Z1，行星轮的齿数为 Z2，太阳轮的角速度为ω1，行星轮的角速度为ω2。

那么，行星齿轮传动比计算公式可以表示为：传动比 = ω1 / ω2 = Z1 / Z2在实际应用中，行星齿轮传动比通常是瞬时传动比，即太阳轮和行星轮的瞬时角速度比。

但是，在某些特殊情况下，例如当太阳轮和行星轮的转速相同时，瞬时传动比就会变为恒定的平均传动比。

行星齿轮传动比具有以下特点：1.行星齿轮传动比是瞬时传动比，即随太阳轮和行星轮的角速度变化而变化。

2.行星齿轮传动比的计算方法简单，只需要知道太阳轮和行星轮的齿数和角速度即可。

3.行星齿轮传动比可以帮助我们了解传动系统的工作状态，以及调整传动系统中的参数，以达到最佳的工作效果。

应用行星齿轮传动比时，需要注意以下事项：1.确保行星齿轮传动比的计算准确无误，以免影响传动系统的工作效果。

2.根据行星齿轮传动比的计算结果，及时调整传动系统中的参数，以达到最佳的工作效果。

3.注意行星齿轮传动比的变化规律，以便在传动系统出现异常时，及时进行处理。

行星齿轮传动比计算公式摘要：一、行星齿轮传动简介1.行星齿轮传动定义2.行星齿轮传动结构二、行星齿轮传动比计算公式1.行星齿轮传动比定义2.计算公式a.齿数比b.转速比c.传动比三、行星齿轮传动比计算实例1.实例一2.实例二四、行星齿轮传动比的实际应用1.工业机械2.汽车传动系统正文：行星齿轮传动是一种常见的机械传动方式，由太阳轮、行星轮、环形齿轮和行星架组成。

它具有体积小、重量轻、传动比稳定等优点，广泛应用于各种工业机械和汽车传动系统等领域。

在行星齿轮传动中，传动比是一个重要的参数，用于描述太阳轮、行星轮和环形齿轮之间的转速关系。

传动比的计算公式如下：a.齿数比：iz1/iz2，表示主动轮齿数与从动轮齿数之比。

b.转速比：n1/n2，表示主动轮转速与从动轮转速之比。

c.传动比：iz1/iz2 × n1/n2，表示主动轮齿数与从动轮齿数之比与主动轮转速与从动轮转速之比的乘积。

下面通过两个实例来说明行星齿轮传动比的计算方法：实例一：假设有一个行星齿轮传动系统，主动轮齿数为40，从动轮齿数为20，主动轮转速为1000r/min，从动轮转速为2000r/min。

求传动比。

解答：根据传动比公式，可得：齿数比：iz1/iz2 = 40/20 = 2转速比：n1/n2 = 1000/2000 = 0.5传动比：iz1/iz2 × n1/n2 = 2 × 0.5 = 1因此，该行星齿轮传动比的值为1。

实例二：假设有一个行星齿轮传动系统，主动轮齿数为30，从动轮齿数为15，主动轮转速为1500r/min，从动轮转速为3000r/min。

求传动比。

解答：根据传动比公式，可得：齿数比：iz1/iz2 = 30/15 = 2转速比：n1/n2 = 1500/3000 = 0.5传动比：iz1/iz2 × n1/n2 = 2 × 0.5 = 1因此，该行星齿轮传动比的值为1。

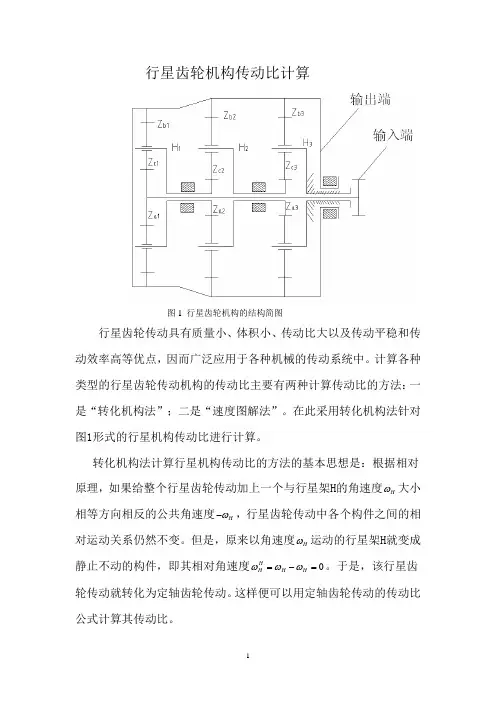
行星齿轮机构传动比计算图1 行星齿轮机构的结构简图行星齿轮传动具有质量小、体积小、传动比大以及传动平稳和传动效率高等优点，因而广泛应用于各种机械的传动系统中。

计算各种类型的行星齿轮传动机构的传动比主要有两种计算传动比的方法：一是“转化机构法”；二是“速度图解法”。

在此采用转化机构法针对图1形式的行星机构传动比进行计算。

转化机构法计算行星机构传动比的方法的基本思想是：根据相对原理，如果给整个行星齿轮传动加上一个与行星架H 的角速度H ω大小相等方向相反的公共角速度H ω-，行星齿轮传动中各个构件之间的相对运动关系仍然不变。

但是，原来以角速度H ω运动的行星架H 就变成静止不动的构件，即其相对角速度0HHH H ωωω=-=。

于是，该行星齿轮传动就转化为定轴齿轮传动。

这样便可以用定轴齿轮传动的传动比公式计算其传动比。

总传动比 1a bi ωω=，其中1a ω、b ω为主动件和被动件的角速度 根据该计算方法的基本思想，结合图1的具体结构，得到第一级传动比为：1111111a H b b H a zi z ωωωω-==-- (1)同理第二级和第三级传动比分别为：2222222a H b b H a zi z ωωωω-==-- (2)3333333a Hb b H a zi z ωωωω-==-- (3)根据图1中的实际结构，及三个内齿圈连接为一体，且第三级行星架H3固定，所以有123b b b b ωωωω===，30H ω= ， 12H a ωω= ，23H a ωω= （4） 由(3)式可得3333233b b a b b H a a z zz z ωωωω=-⨯=-⨯= (5) 把（5）式代入（2）式可得32223232223b a b a H a b b b H a b ba z z zz z z ωωωωωωωω+⨯-==--+⨯所以得23323321233233()[(1)]b b b b b b a b b b b H a a a a a a z z z z z zz z z z z z ωωωωωω=-⨯+⨯-⨯=-⨯⨯++= (6) 把（6）式代入（1）式可得：2331112331233111233[(1)][(1)]b b b a b a H a a a b b b b b H a b b a a a z z z z z z zz z z z z z z ωωωωωωωω+⨯⨯++-==--+⨯⨯++ (7)式（7）可化简为：123323323323312332331233233[(1)][(1)]1[(1)]1[(1)]a b b b b b b b a a a a a a b b b b b b b a a a a a a a z z z z z zi z z z z z z zz z zz z zz z z z z z z ωω+⨯+++⨯++==-+⨯+++⨯++ （8）由（8）式可得123323312332331[(1)][(1)]b b b b b b b a a a a a a a z z z z z z z i z z z z z z z ⎧⎫=-⨯+⨯++-⨯++⎨⎬⎩⎭11233233112332331233112331[(1)][(1)][(1)](1)b b b b b b b b a a a a a a a a b b b b b a a a a a z z z z z z z z z z z z z z z z z z z z z z z z z z =--⨯⨯++-⨯++=--⨯++⨯+所以12331123311(1)[(1)](1)b b b b b a a a a a z z z z z i z z z z z -=-+-⨯++⨯+ 12331233(1)[1(1)]b b b b a a a a z z z zz z z z =-+⨯+⨯++ 123123(1)(1)(1)b b b a a a z z z z z z =-+⨯+⨯+ 所以得总传动比1231231(1)(1)(1)b b b a a a z z zi z z z =-+⨯+⨯+ 即为该种行星结构的传动比。

行星齿轮传动比计算在《机械原理》上，行星齿轮求解是通过列一系列方程式求解，其求解过程繁琐容易出错，其实用不着如此，只要理解了传动比eab i 的含义，就可以很快地直接写出行星齿轮的传动比，其关键是掌握几个根据e ab i 的含义推导出来公式，随便多复杂的行星齿轮传动机构，根据这几个公式都能从头写到尾直接把其传动比写出来，而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。

一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1 acx a bx abci i i = ―――――――――――――――――――――――――2 a cb abc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后，不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。

关键是要善于选择中间的一些部件作为参照，使其最后形成都是定轴传动，所以这些参照基本都是一些行星架等例如：在此例中，要求出e ab i ＝，如果行星架固定不动的话，这道题目就简单多了，就是一定轴传动。

所以我们要想办法把e ab i 变成一定轴传动，所以可以根据公式a cx a bx a bci i i =将x 加进去， 所以可以得出：e bx e ax eab i i i =要想变成定轴传动，就要把x 放到上面去，所以这里就要运用第一个公式1=+c ba abc i i 了，所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。

定轴传动的传动比就好办了，直接写出来就可以了。

即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构：已知其各轮的齿数为z 1=100，z 2=101，z 2’ =100 ，z 3=99。

12.2 行星轮系传动比的计算12.2.1 行星轮系的分类若轮系中，至少有一个齿轮的几何轴线不固定，而绕其它齿轮的固定几何轴线回转，则称为行星轮系。

如图所示的轮系中，齿轮2除绕自身轴线回转外，还随同构件H一起绕齿轮1的固定几何轴线回转，该轮系即为行星轮系。

齿轮2称为行星轮，H称为行星架或系杆，齿轮1、3称为太阳轮。

运动演示拆装通常将具有一个自由度的行星轮系称为简单行星轮系，如下图所示；将具有两个自由度的行星轮系称为差动轮系，如下图所示。

12.2.2 行星轮系的传动比计算不能直接用定轴轮系传动比的公式计算行星轮系地传动比。

可应用转化轮系法，即根据相对运动原理，假想对整个行星轮系加上一个与n H大小相等而方向相反的公共转速-n H，则行星架被固定，而原构件之间的相对运动关系保持不变。

这样，原来的行星轮系就变成了假想的定轴轮系。

这个经过一定条件转化得到的假想定轴轮系，称为原行星轮系的转化机构。

转化轮系运动演示利用定轴轮系传动比的计算方法，可列出转化轮系中任意两个齿轮的传动比。

1，3轮的传动比为：一般地，n G和n K为行星轮系中任意两个齿轮G和K的转速，在使用上式时应特别注意：（1）公式只适用于圆柱齿轮组成的行星轮系。

对于由圆锥齿轮组成的行星轮系，当两太阳轮和行星架的轴线互相平行时，仍可用转化轮系法来建立转速关系式，但正、负号应按画箭头的方法来确定。

并且，不能应用转化机构法列出包括行星轮在内的转速关系。

（2）将已知转速代入公式时，注意“+”、“-”号。

一方向代正，另一方向代负号。

求得的转速为正，说明与正方向一致，反而反之。

运动演示拆装例12-2 行星轮系如图所示。

已知Z1=15,Z2=25,Z3=20,Z4=60,n1=200r/min,n4=50r/min,且两太阳轮1、4转向相反。

试求行星架转速n H及行星轮转速n3。

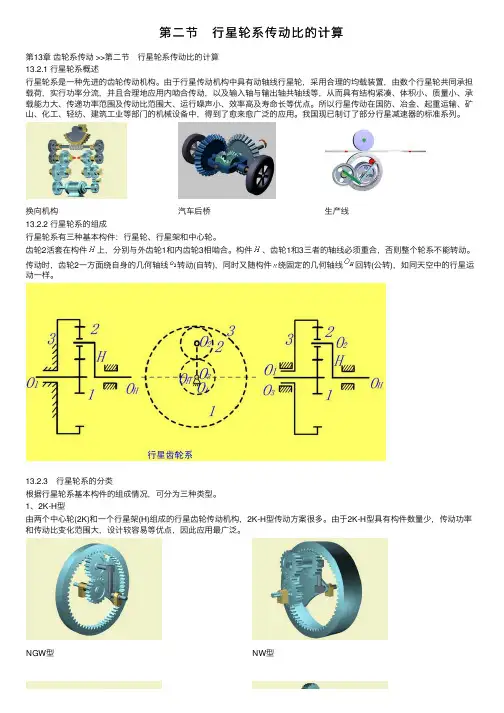
第⼆节　⾏星轮系传动⽐的计算第13章齿轮系传动 >>第⼆节　⾏星轮系传动⽐的计算13.2.1 ⾏星轮系概述⾏星轮系是⼀种先进的齿轮传动机构。

由于⾏星传动机构中具有动轴线⾏星轮，采⽤合理的均载装置，由数个⾏星轮共同承担载荷，实⾏功率分流，并且合理地应⽤内啮合传动，以及输⼊轴与输出轴共轴线等，从⽽具有结构紧凑、体积⼩、质量⼩、承载能⼒⼤、传递功率范围及传动⽐范围⼤、运⾏噪声⼩、效率⾼及寿命长等优点。

所以⾏星传动在国防、冶⾦、起重运输、矿⼭、化⼯、轻纺、建筑⼯业等部门的机械设备中，得到了愈来愈⼴泛的应⽤。

我国现已制订了部分⾏星减速器的标准系列。

换向机构汽车后桥⽣产线13.2.2 ⾏星轮系的组成⾏星轮系有三种基本构件：⾏星轮、⾏星架和中⼼轮。

齿轮2活套在构件上，分别与外齿轮1和内齿轮3相啮合。

构件、齿轮1和3三者的轴线必须重合，否则整个轮系不能转动。

传动时，齿轮2⼀⽅⾯绕⾃⾝的⼏何轴线转动(⾃转)，同时⼜随构件绕固定的⼏何轴线回转(公转)，如同天空中的⾏星运动⼀样。

13.2.3　⾏星轮系的分类根据⾏星轮系基本构件的组成情况，可分为三种类型。

1、2K-H型由两个中⼼轮(2K)和⼀个⾏星架(H)组成的⾏星齿轮传动机构，2K-H型传动⽅案很多。

由于2K-H型具有构件数量少，传动功率和传动⽐变化范围⼤，设计较容易等优点，因此应⽤最⼴泛。

NGW型NW型NN型WW型2、3K型有三个中⼼轮(3K)，其⾏星架不传递转矩，只起⽀承⾏星轮的作⽤。

3、 K-H-V型由⼀个中⼼轮(K)、⼀个⾏星架(H)和⼀个输出机构组成，输出轴⽤V表⽰3K型K-H-V型⾏星轮系按啮合⽅式来命名有NGW型、NW型和NN型等等。

N表⽰内啮合，W表⽰外啮合，G表⽰公⽤的⾏星轮。

13.2.3　⾏星轮系传动⽐的计算⾏星轮系与定轴轮系的根本差别在于⾏星轮系中具有转动的⾏星架，从⽽使得⾏星轮既有⾃转⼜有公转。

因此，⾏星轮系各构件间的传动⽐不能直接引⽤定轴轮系传动⽐的公式来计算。

行星速比计算1 什么是行星速比？行星速比（Planetary Gear Ratio）是指行星齿轮机构中太阳轮与行星轮的转速比。

行星齿轮机构是一种复杂的传动机构，由中心轴（也称原动轴）、圆盘（也称太阳轮）、行星轮和行星架等组成。

其中太阳轮和行星轮之间的速比是行星速比。

2 行星速比计算公式行星速比可以通过下面的公式计算：R = 1 + T1/T2其中，R为行星速比，T1为行星挂接在行星架上的轮齿数，T2为太阳轮挂接的轮齿数。

3 通过简单的数学问题理解行星速比计算公式下面我们通过一个简单的数学问题来理解这个公式。

假设我们有一个行星齿轮机构，其中行星轮挂接在行星架上，行星轮与太阳轮的轴心距为12毫米。

行星轮上有20个齿，太阳轮上有60个齿。

问太阳轮每转一圈，行星轮转了多少圈？首先，我们可以通过太阳轮每转一圈，行星轮转的轮齿数来计算它们之间的速比。

T1/T2 = 20/60 = 1/3然后，我们可以用行星速比公式来计算行星速比：R = 1 + T1/T2 = 1 + 1/3 = 4/3最后，我们可以得出行星轮每转一圈时，太阳轮需要转4/3圈。

4 行星速比的应用行星齿轮机构广泛应用于机械传动、液压机械和自动控制等领域。

由于其结构紧凑、传动平稳、转矩大等优点，因此在工业生产和机械设计中有着广泛的应用。

行星速比也可以用于设计步进电机和减速器。

5 结论行星速比是行星齿轮机构中太阳轮和行星轮之间的速比。

通过行星速比公式可以计算出太阳轮每转一圈，行星轮需要转的圈数。

行星速比具有广泛的应用，可以用于机械传动、自动控制、步进电机和减速器的设计等方面。

行星齿轮机构传动比计算方法Key words: epicyclic gear train; speed ratio; compute way.随着行星齿轮减速器以及行星齿轮传动在变速箱中的广泛应用，对行星齿轮传动的了解和掌握已成为工程技术人员的必要技能。

但是，对于刚接触行星齿轮传动的工程技术人员来说，行星齿轮传动的速比计算比较不容易理解和掌握。

本文通过对各类参考资料及教科书中的行星齿轮传动速比计算方法进行总结归纳，并针对常用的最具代表性的2K-H型行星齿轮传动，分别用不同方法对其传动特性方程进行了推导论证。

行星齿轮传动或称周转轮系。

根据《机械原理》[1]上的定义，我们可把周转轮系分为差动轮系和行星轮系。

为理解方便，本论文所讨论限于2K-H型周转轮系。

关于行星齿轮传动（周转轮系）的速比计算方法，归纳起来有两大类四种方法，分别为由行星架固定法和力矩法组成的分析法；由速度图解法和矢量法组成的图解法[2]。

矢量图解法一般适用于圆锥齿轮组成的行星齿轮传动，在此不作介绍；下面分别运用其它三种计算方法对2K-H型周转轮系的传动特性方程（1）进行推导。

1－太阳轮 2－行星轮 3－内齿圈 H －行星架 图1 行星齿轮传动Fig 1 Epicyclic gear train0)1(31=++-αωωαωH （1） 结合图1，式中1ω为太阳轮1的转速、Hω为行星架H 转速、3ω为内齿圈3转速、α为内齿圈3与太阳轮1的齿数比即13Z Z =α。

1 行星架固定法机械专业教科书上一般介绍的都是此种方法，也可叫转化机构法。

其理论是一位名叫Wlies 的科学家于1841年提出的，即“一个机构整体的绝对运动并不影响其内部各构件间的相对运动” [3]，就像手表的时针、分针、秒针的相对运动不会因带表人的行动而变化。

如图2所示，其中太阳轮1、行星轮2、内齿圈3、行星架H 的转速分别为Hωωωω、、、321。

我们假定整个行星轮系放在一个绕支点O 旋转的圆盘上，此圆盘的转速为 H ω-。

行星齿轮传动比计算在《机械原理》上，行星齿轮求解是通过列一系列方程式求解，其求解过程繁琐容易出错，其实用不着如此，只要理解了传动比e ab i 的含义，就可以很快地直接写出行星齿轮的传动比，其关键是掌握几个根据e ab i 的含义推导出来公式，随便多复杂的行星齿轮传动机构，根据这几个公式都能从头写到尾直接把其传动比写出来，而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。

一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1a cx a bx abci i i = ―――――――――――――――――――――――――2 a cb abc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后，不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。

关键是要善于选择中间的一些部件作为参照，使其最后形成都是定轴传动，所以这些参照基本都是一些行星架等例如：在此例中，要求出e ab i ＝？，如果行星架固定不动的话，这道题目就简单多了，就是一定轴传动。

所以我们要想办法把e ab i 变成一定轴传动，所以可以根据公式a cx a bx a bci i i =将x 加进去， 所以可以得出：e bx e ax eab i i i =要想变成定轴传动，就要把x 放到上面去，所以这里就要运用第一个公式1=+c ba abc i i 了，所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在e ab i 就变成了两个定轴传动之间的关系式了。

定轴传动的传动比就好办了，直接写出来就可以了。

即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构：已知其各轮的齿数为z 1=100，z 2=101，z 2’ =100 ，z 3=99。

行星齿轮常见速比计算公式行星齿轮是一种常见的传动装置，它由外齿圈、内齿圈和行星轮组成。

行星齿轮传动系统具有结构紧凑、传动比范围广、承载能力强等优点，因此在各种机械设备中得到广泛应用。

在设计行星齿轮传动系统时，需要计算速比，以确保传动系统的性能满足设计要求。

本文将介绍行星齿轮常见的速比计算公式，帮助读者更好地理解和应用行星齿轮传动系统。

行星齿轮传动系统的速比是指输入轴和输出轴的转速之比。

在行星齿轮传动系统中，速比可以通过以下公式计算：速比 = (1 + Zs/Zp) (1 + Zr/Zp)。

其中，Zs为太阳轮的齿数，Zp为行星轮的齿数，Zr为内齿圈的齿数。

这个公式适用于一般的行星齿轮传动系统，通过输入轴和输出轴的齿轮组合来计算速比。

除了上述公式外，还有一些特殊情况下的速比计算公式。

例如，当行星轮固定不动时，速比可以简化为：速比 = -Zs/Zr。

这个公式适用于固定行星轮的情况，通过太阳轮和内齿圈的齿轮组合来计算速比。

另外，当内齿圈固定不动时，速比可以简化为：速比 = (Zs + Zp)/Zr。

这个公式适用于固定内齿圈的情况，通过太阳轮和行星轮的齿轮组合来计算速比。

以上是行星齿轮常见的速比计算公式，通过这些公式可以方便地计算行星齿轮传动系统的速比。

在实际应用中，设计人员需要根据具体的传动要求和参数，选择合适的齿轮组合，以满足传动系统的性能要求。

同时，还需要考虑传动效率、扭矩传递、轴向尺寸等因素，综合考虑来确定最终的齿轮组合方案。

除了速比计算公式外，还需要注意行星齿轮传动系统的设计和制造工艺。

例如，齿轮的加工精度、装配间隙、润滑方式等都会影响传动系统的性能和寿命。

因此，在设计和制造行星齿轮传动系统时，需要综合考虑各种因素，以确保传动系统能够稳定可靠地工作。

在实际的工程应用中，行星齿轮传动系统广泛应用于各种机械设备中，如汽车变速箱、工程机械、航天器等。

通过合理的设计和制造，行星齿轮传动系统可以实现高效、可靠的动力传递，满足不同工况下的传动需求。

中速磨煤机减速机各阶齿轮啮合频率计算一．中速磨减速机传动结构简图二．行星轮部分传动比i = N2/Nh = 1 + Zr/Zs rpm 三．行星架转速Nh = N2/i rpm四．太阳轮啮合频率GMFs = N2×Zs/60 Hz 五．行星轮的转速Np= (N2-Nh)×Zs / Zp Rpm 六．行星轮啮合频率GMFp= Np×Zp/60Hz七．减速机输入轴齿轮啮合频率GMF1 = N1*Z1/60 Hz八．计算举例广西贵港电厂中速磨电机功率630Kw输入轴转速990 rpm减速机输入转速为990 Rpm输入伞齿轮齿数Z1=11大伞齿轮齿数Z2=54太阳轮齿数Zs=16行星轮齿数Zp=49大齿圈齿数Zr=116计算各阶啮合频率太阳轮转速Ns=990×11/54=201.67 Rpm太阳轮啮合频率GMFs=Ns×Zs/60=201.67×16/60= 53.78 Hz输入高速轴齿轮啮合频率GMF1=990×11/60 = 181.5 Hz行星减速机的传动比i = N2/Nh = 1 + Zr/Zs=1+116/16=8.25减速机输出转速Nh=N2/i=201.67/8.25=24.44 Rpm行星轮的转速Np= (N2-Nh)×Zs / Zp = (201.67-24.44)×16/49 = 57.87 rpm行星轮啮合频率GMFp=Np×Zp/60 =57.87×49/60 = 47.26 Hz2014.7.6 lsy。

行星传动传动比及啮合频率计算特征频率主要包含转频和啮合频率，根据传动比计算的结果，可以相应的算出每个齿轮相对应的转速n ，则转频60i i f n =，齿轮啮合频率等于该齿轮的转频乘以它的齿数。

相互啮合的两个齿轮的啮合频率是相等的。

即zi i i f f z =⨯。

而齿轮的振动谱就是以该基频（zi f ）波和高次谐波所组成的谱，因此在故障诊断中具有重大意义。

又因为相互啮合的两个齿轮的啮合频率是相等的，所以一组行星轮系当中只要计算中心论转速即可。

1a 1b 1c 2a 2b 2c Input ShaftOutput Shaft2d 1d 3d 4d齿轮模型n –输入转速；Za1–第一级太阳轮齿数；Zb1 –第一级行星轮齿数；Zc1–第一级内齿圈齿数； Za2 –第二级太阳轮齿数；Zb2 –第二级行星轮齿数；Zc2 –第二级内齿圈齿数；（1） 一级行星轮系：111111a H c c H a n n z n n z -=-- 其中，n n n a c ==11,0 ，则 )1//(11111+==a c a Hb z z n n n =n 61（2） 二级行星轮系：222222a H c c H a n n zn n z -=--其中，122,0H a c n n n ==，则)1//(22222+==a c a H b z z n n n =2327a n 行星轮系级: 传动比i =192/7 （3）平行轴：中间低速级： 传动比i1= 小大n n =100/29高速级： 传动比i2= 小大n n =2.5 平行轴传动比：i=8.6 总传动比：i=232齿轮箱振动特征频率 1. 啮合频率:1）转速同步频率 n f = n/60 式中，n 为轴转速（转/分）。

2）定轴齿轮啮合频率n f = nz/60 式中，n 为轴转速（转/分）， r z 为齿轮齿数。

3）行星轮系，啮合频率用下式计算： m f = a b a c b z f f z f ⨯-=⨯)( 式中，b n 为行星轮架转速（转/分），c z 为内齿圈齿数，a f 为太阳轮转频，a z 为太阳轮齿数。

啮合功率法计算行星轮效率行星轮是一种常见的传动装置，具有高效率和大承载能力的特点。

为了评估行星轮的性能，可以使用啮合功率法进行计算。

行星轮的效率是指输入功率与输出功率之比，即输出功率与输入功率的比值。

本文将介绍啮合功率法的基本原理和计算步骤，并以一个实际案例进行说明。

啮合功率法是一种基于啮合理论的计算方法，可以准确地评估行星轮的效率。

它的基本原理是根据行星轮的结构和工作原理，通过计算输入和输出轴的功率来确定行星轮的效率。

具体步骤如下：步骤一：确定输入和输出轴的功率。

在行星轮传动系统中，输入轴是驱动轴，输出轴是被驱动轴。

通过测量输入和输出轴的转速和扭矩，可以计算出它们的功率。

步骤二：计算行星轮的传动比。

行星轮的传动比是指输出轴的转速与输入轴的转速之比。

它可以通过行星轮的齿轮比和齿轮的啮合关系来确定。

步骤三：计算行星轮的传动效率。

行星轮的传动效率是指输出功率与输入功率之比。

它可以通过计算输入和输出轴的功率，并将输出功率除以输入功率得到。

为了更好地理解啮合功率法的计算过程，下面以一个实际案例进行说明。

假设有一个行星轮传动系统，齿轮传动比为4:1，输入轴的转速为1000转/分钟，扭矩为100Nm，输出轴的转速为250转/分钟。

根据上述步骤，可以进行如下计算：步骤一：输入轴的功率为：输入功率 = 输入扭矩× 输入转速= 100Nm × (1000转/分钟)= 100000W输出轴的功率为：输出功率 = 输出扭矩× 输出转速= 100Nm × (250转/分钟)= 25000W步骤二：行星轮的传动比为4:1，即输出轴的转速是输入轴的1/4。

步骤三：行星轮的传动效率为：传动效率 = 输出功率 / 输入功率= 25000W / 100000W= 0.25根据上述计算，可以得出该行星轮传动系统的效率为0.25，即25%。

这意味着行星轮传动系统的输出功率只有输入功率的四分之一。