1随机事件与事件间的关系与运算介绍

简述随机事件之间的关系随机事件之间的关系可以通过概率论中的概念来描述。

在概率论中，随机事件是指在一定条件下可能发生或不发生的结果。

这些事件之间的关系可以从以下几个方面来理解：1. 独立性：如果两个随机事件A和B的发生互不影响，即A的发生不影响B的发生，B的发生也不影响A的发生，那么我们称A和B是独立的。

数学上，如果P(A)和P(B)是事件A和B的概率，且P(A ∩ B) = P(A)P(B)，则A和B是独立的。

2. 条件概率：在给定一个事件B发生的条件下，事件A发生的概率称为A 在B发生的条件下的条件概率，记为P(A|B)。

条件概率反映了在一定的背景下，事件A发生的可能性。

3. 互斥性：如果两个事件A和B不能同时发生，即它们没有共同的样本点，那么我们称A和B是互斥的。

互斥事件的关系可以通过概率加法公式来描述，即P(A ∪ B) = P(A) + P(B)。

4. 包含关系：如果一个事件A的发生必然导致事件B的发生，那么我们称B是A的子事件，或者说A包含B。

这种关系可以用来描述事件之间的层次结构。

5. 并事件和交事件：事件的并是指两个或多个事件中至少有一个发生的情况，而事件的交是指两个或多个事件同时发生的情况。

并事件的概率不小于任何参与事件的概率，而交事件的概率小于等于任何参与事件的概率。

6. 对立事件：如果两个事件A和B互斥且并事件的概率为1，即P(A ∪ B) = 1，那么A和B是对立事件。

对立事件的概率和为1，即P(A) + P(B) = 1。

这些关系帮助我们理解和分析随机事件之间的相互作用，并在实际应用中如统计学、概率论、随机过程等领域中有着重要的应用。

通过这些关系的运用，我们可以更好地预测和理解随机现象。

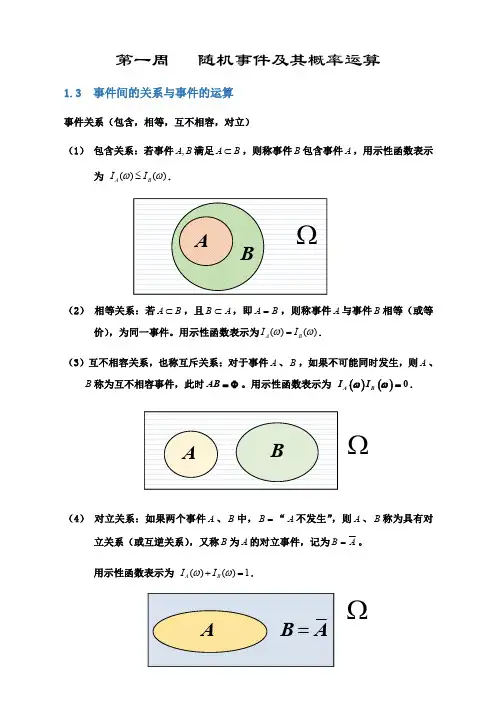
第一周随机事件及其概率运算1.3事件间的关系与事件的运算事件关系（包含，相等，互不相容，对立）（1）包含关系：若事件,A B 满足A B⊂，则称事件B 包含事件A ，用示性函数表示为()()ωω≤A B I I .（2）相等关系：若A B ⊂，且A B ⊂，即B A =，则称事件A 与事件B 相等（或等价），为同一事件。

用示性函数表示为()()A B I I ωω=.（3）互不相容关系，也称互斥关系：对于事件A 、B ，如果不可能同时发生，则A 、B 称为互不相容事件，此时AB =Φ。

用示性函数表示为()()0A B I I ωω=.（4）对立关系：如果两个事件A 、B 中，=B “A 不发生”，则A 、B 称为具有对立关系（或互逆关系），又称B 为A 的对立事件，记为A B =。

用示性函数表示为()()1ωω+=A B I I .ΩΩ*********************************************************事件运算（和，积，差，交换律，结合律，分配律，结合律，对偶律）（1）事件的和：事件A 与事件B 的并集构成的事件称为事件A 与事件B 的和事件，记为A B 或A B +，即{}|A B x x A x B =∈∈ 或，如图所示的阴影部分.显然，当且仅当事件A 与事件B 至少有一个发生时，事件A B 才发生。

n 个事件n A A A ,,,21 的和事件，即为n 个集合的并集 n k k A 1=。

（2）事件的积（或交）：事件A 与事件B 的交集构成的事件称为事件A 与事件B 的积（或交）事件，事件A 与事件B 同时发生。

记为A B 或AB 。

n 个事件n A A A ,,,21 的积事件，即为n 个集合的交集 nk k A 1=。

（3）事件的差：事件A 与事件B 的差集所构成的事件称为事件A 与事件B 的差事件，记为B A -。

{}|A B x x A x B AB -=∈∉=且。

随机事件的关系与运算随机事件是指在一定条件下具有随机性质的事件，其发生与否是由随机因素决定的。

在随机事件中，我们需要对其进行运算，以便得到更加准确的结果。

本文将从随机事件的关系与运算角度，对随机事件的基本概念、性质、运算规则等进行探讨。

一、随机事件的基本概念与性质随机事件是指在一定条件下具有随机性质的事件，其发生与否是由随机因素决定的。

随机事件的基本概念包括：样本空间、随机事件、必然事件和不可能事件。

样本空间是指一个试验中所有可能的结果构成的集合，记作S。

随机事件是指样本空间S中的一个子集，即一个具有一定概率的事件。

必然事件是指在样本空间中所有结果都属于该事件的事件，记作Ω。

不可能事件是指在样本空间中没有任何结果属于该事件的事件，记作∅。

随机事件具有以下性质：1. 互斥性：若两个事件A和B之间没有公共结果，则称它们互斥。

2. 相对补集：若事件A的发生导致事件B的不发生，则称事件A是事件B的补事件，记作A的补集，即A^c。

3. 包含关系：若事件A的发生导致事件B的发生，则称事件A包含事件B，记作A⊇B。

二、随机事件的运算规则在随机事件的运算中，我们需要对事件之间的关系进行分析和计算。

随机事件的运算包括并、交、差和补四种运算。

1. 并运算并运算是指将两个事件A、B的结果集合并为一个结果集的操作，用符号“∪”表示。

即：A∪B={x|x∈A或x∈B}。

并运算的性质：（1）交换律：A∪B=B∪A。

（2）结合律：(A∪B)∪C=A∪(B∪C)。

（3）分配律：A∩(B∪C)=(A∩B)∪(A∩C)。

2. 交运算交运算是指将两个事件A、B的公共结果构成一个新的事件的操作，用符号“∩”表示。

即：A∩B={x|x∈A且x∈B}。

交运算的性质：（1）交换律：A∩B=B∩A。

（2）结合律：(A∩B)∩C=A∩(B∩C)。

（3）分配律：A∪(B∩C)=(A∪B)∩(A∪C)。

3. 差运算差运算是指事件A中除去事件B的结果所构成的新事件，用符号“-”表示。

有关随机事件关系和运算的例析随机事件是概率论中的基础概念，是指在某一实验中可能发生的事件。

在实际应用中，我们常常需要对多个随机事件进行关系和运算，以求得更为准确的结果。

下面，我们将通过一些例子，来深入探究随机事件的关系和运算。

一、事件的关系1. 包含关系当事件A包含事件B时，我们可以表示为 AB。

例如：在掷一枚骰子的实验中，事件A表示掷出的点数是偶数，事件B表示掷出的点数是2。

显然，事件B包含在事件A中，即 AB。

2. 相等关系当事件A和事件B所包含的样本点完全相同时，我们可以表示为A=B。

例如：在掷一枚骰子的实验中，事件A表示掷出的点数是偶数，事件B表示掷出的点数不是偶数。

显然，事件A和事件B所包含的样本点完全相同，即 A=B。

3. 互斥关系当事件A和事件B所包含的样本点没有交集时，我们可以表示为A∩B=。

例如：在掷一枚骰子的实验中，事件A表示掷出的点数是偶数，事件B表示掷出的点数是奇数。

显然，事件A和事件B所包含的样本点没有交集，即 A∩B=。

4. 独立关系当事件A和事件B的发生与否互不影响时，我们可以表示为P(A|B)=P(A) 或 P(B|A)=P(B)。

例如：在掷一枚骰子的实验中，事件A表示掷出的点数是偶数，事件B表示掷出的点数大于3。

显然，事件A和事件B的发生与否互不影响，即 P(A|B)=P(A) 或 P(B|A)=P(B)。

二、事件的运算1. 并集运算当事件A和事件B中至少有一个发生时，我们可以表示为 A∪B。

例如：在掷一枚骰子的实验中，事件A表示掷出的点数是偶数，事件B表示掷出的点数是3。

显然，事件A和事件B中至少有一个发生，即 A∪B。

2. 交集运算当事件A和事件B同时发生时，我们可以表示为 A∩B。

例如：在掷一枚骰子的实验中，事件A表示掷出的点数是偶数，事件B表示掷出的点数是4。

显然，事件A和事件B同时发生，即 A∩B。

3. 补集运算当事件A不发生时，我们可以表示为 A'。

3. 1随机事件及其运算.教学要求本节要求学生掌握随机试验及随机事件的概念，能够熟练掌握事件之间的关系，并会运用事件运算的性质求解一些具体问题．知识点1．随机试验的概念2．随机事件的概念3．事件间的关系4．事件运算的性质3.1.1 随机试验的概念在客观世界中, 存在着两类不同的现象.1.确定性现象: 在一定的条件下, 必然要出现某一种结果的现象. 我们前面所学的微积分﹑线性代数等都是用来研究客观世界中的“确定性现象”的数量规律及其存在形式的．例如, 在标准大气压下, 水加热到100℃, 必然沸腾等都是确定性现象．2.随机性现象: 在一定的条件下, 可能结果不止一个而事先无法确定的现象，例如,抛一枚硬币, 其结果可能是正面向上, 也有可能反面向上, 每次抛掷之前无法确定其结果是什么；一袋中装有红﹑白两种颜色的球, 从袋中任取一球, 其颜色有可能是红色的, 也有可能是白色的, 在每次取球之前无法确定其颜色；这些都是随机性现象. 概率统计就是研究随机现象数学规律的一个数学分支.随机现象广泛地存在于客观世界的各个领域, 其内在规律一般可在相同条件下通过大量重复试验而获得.定义. 在概率统计中, 我们把对随机现象的一次观测称为一次随机试验, 简称为试验.概率论中所研究的试验具有如下特点:(1)可以在相同的条件下重复进行；(2)每次试验的结果具有多种可能性,并且事先能明确试验的所有可能结果；(3)每次试验之前不能确定该次试验将出现哪一种结果.一次试验结果的不确定性, 表现了随机现象的偶然性的一面, 而在大量重复试验的条件下, 显现出来的统计规律性, 表现了它的必然性一面, 这就是随机现象的二重性——偶然性和统计必然性之间的辨证关系. 随机现象的二重性充分说明, 随机现象是可以认识的. 研究随机现象是为了掌握随机现象的统计规律性.1813.1.2 随机事件的概念定义. 在随机试验中, 可能出现或可能不出现的结果称为随机事件, 简称为事件, 常用大写字母A、B、C等表示.定义. 在一定条件下, 必然发生的事件, 称为必然事件,记为Ω.定义. 在一定条件不, 必然不发生的事件, 称为不可能事件, 记为Φ.定义. 我们把随机试验的每一可能出现的直接结果即不可能再分解的事件称为基本事件, 记为ω.定义: 基本事件的全体所组成的集合称为基本事件组. 因此, 基本事件组作为一个事件, 它是必然事件, 仍记为 Ω.定义. 从几何意义看, 随机试验的每一个可能的结果叫做样本点, 样本点的全体称为样本空间, 故样本空间与基本事件组的关系是 1一 1对应关系, 记为：Ω={ω1,ω2,… ,ωn}样本空间(基本事件组)、基本事件、随机事件之间的关系见图:显然，事件就是样本空间的某种子集.例3.1.1抛一枚骰子的试验中E, 观察其出现点数.A1=“出现1点”, A2=“出现2点”, A3=“出现3点”, A4=“出现4点”, A5=“出现5点”, A6=“出现6点”都是基本事件；A7=“出现偶数点”, A8=“出现点数大于3点”等都是事件, 但不是基本事件；A9=“出现点数小于7”是必然事件,A10=“出现点数大于6”是不可能的事件, 在此试验中,Ω={ A1,,A2, A3,A4, A5, A6}.1821833.1.3事件间的关系事件既然是样本空间的某种子集, 所以事件的关系与运算应与集合的关系与运算完全对应.设随机试验E 的样本空间为Ω, 而A 、B 、A k ( k =1, 2, …)是E 的事件.(1)包含与相等若事件A 发生必然导致事件B 发生, 则称事件B 包含事件A , 记为B ⊃ A 或A ⊂ B , 特别地规定: Φ⊂ A , 且A ⊂Ω.若A ⊂ B 且B ⊂ A ,则称事件A 与B 相等记为A = B .(2)事件的和(或并)事件A 与事件B 至少有一个发生所构成的事件称为事件A 与B 的和事件, 也称为事件的并, 记为A + B .一般地, 推广到n 个事件, 事件A 1,A 2,…,A n 中至少有一个发生所构成的事件称为A 1,A 2,…,A n 这n 个事件的和事件(或并), 记为:∑==+++ni in A A A A 121L.(3)事件的积(或交) 事件A 与事件B 同时发生所构成的事件称为事件A 与事件B 的积事件, 也称为事件的交, 记为AB .一般地, 推广到n 个事件, 事件A 1,A 2,…,A n 同时发生构成的事件称为A 1,A 2,…,A n 这n 个事件的积事件(或交),记为C L n i i n A A A A 121==.(4)事件的差184 若事件A 发生, 而事件B 不发生所构成的事件, 称为事件A 与事件B 的差, 记为A – B.(5)互不相容(互斥)事件 若事件A 与事件B 的积是不可能事件, 即A B =Φ, 则称A 与B 两事件互斥, 或称为互不相容事件。