等价关系与偏序关系复习题答案
- 格式:doc
- 大小:1.74 MB
- 文档页数:6



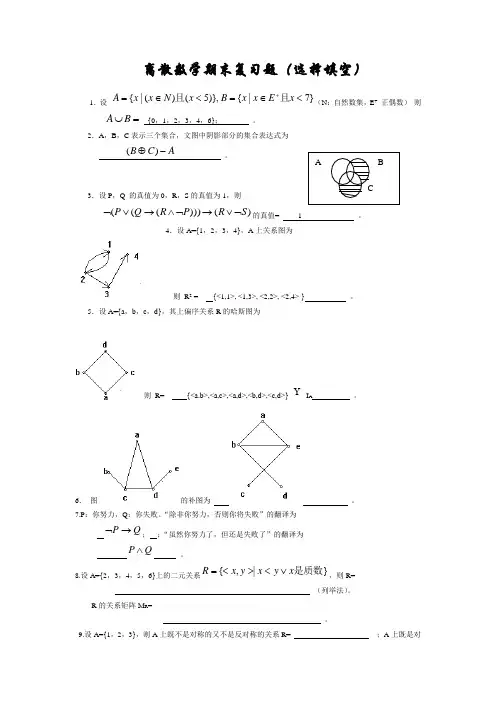
离散数学期末复习题(选择填空)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A {0,1,2,3,4,6}; 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为A CB -⊕)( 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则 )()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 1 。
4.设A={1,2,3,4},A 上关系图为则 R 2 = {<1,1>, <1,3>, <2,2>, <2,4> } 。
5.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= {<a.b>,<a,c>,<a,d>,<b,d>,<c,d>}I A 。
6. 图的补图为 。
7.P :你努力,Q :你失败。
“除非你努力,否则你将失败”的翻译为Q P →⌝; ;“虽然你努力了,但还是失败了”的翻译为Q P ∧ 。
8.设A={2,3,4,5,6}上的二元关系}|,{是质数x y x y x R∨<><=,则R= (列举法)。
R 的关系矩阵M R =。
9.设A={1,2,3},则A 上既不是对称的又不是反对称的关系R= ;A 上既是对AB C称的又是反对称的关系R= 。
10.n 个结点的无向完全图K n 的边数为 )1(21-n n ,欧拉图的充要条件是:图中无奇度结点且连通11.设A={a ,b ,c},A 上二元关系R={< a, a > , < a, b >,< a, c >, < c, c>} ,则s (R )=}a , c ,a , b ,c , c ,c , a ,b , a ,a , a {><><><><><>< 。

专升本《离散数学》一、(共75题,共150分)1. 集合,则()(2分)A.B.C.D.标准答案:B2. 集合,则下列哪个不是的元素()(2分)A.B.C.D.标准答案:B3. 设,在条件且下与()集合相等。
(2分)A.或B.或C.,或D.,或标准答案:C 4. 集合上的关系,则是()(2分)A.自反的B.对称的C.传递且对称的D.反自反且传递的标准答案:B5. 集合,下列不是到的关系的是()(2分)A.B.C.D.标准答案:A6. ,表示求两数的最小公倍数的运算(表示整数集合),对于运算的零元是()(2分)A.B.C.D.不存在标准答案:D7. 下面各集合都是的子集,()集合在普通加法运算下是封闭的。
(2分)A.B.C.D.标准答案:A8. 设集合,“”为整除关系,则代数系统()(2分)A.是域B.是格,不是布尔代数C.是布尔代数D.不是代数系统标准答案:C9. 在()中,补元是唯一的。
(2分)A.有界格B.有补格C.分配格D.有补分配格。
标准答案:D10. 下列语句中,真命题的是( ) (2分)A.请把门关上B.是素数C.D.太阳从西边升起标准答案:B11. 是自然数集,是小于等于关系,则是()。
(2分)A.有界格B.有补格C.分配格D.有补分配格标准答案:C12. 下列函数中,()是双射(2分)A.B.(除以的余数)C.D.标准答案:D13. 设为集合,,在上有()种不同的关系。
(2分)A.B.C.D.标准答案:D14. 设是个结点、条边和个面的连通平面图,则等于()。
(2分)A.B.C.D.标准答案:A15. 对于独异点,则下列说法正确的是()(2分)A.不一定有单位元B.满足交换律C.一定是半群D.独异点就是群标准答案:C16. 群中,当()时,该群一定是循环群。
(2分)A.B.C.D.标准答案:B17. 设,为普通乘法,则是()(2分)A.代数系统B.半群C.群D.都不是标准答案:D18. 下列各图哪个一定是树()(2分)A.有个结点,条边的连通图B.每对结点之间都有路的图C.有个结点,条边的图D.以上说法都不正确标准答案:A19. 在如下各图中是欧拉图的是()(2分)A.B.C.D.标准答案:B20. 下列等价关系正确的是()(2分)A.B.C.D.标准答案:B21. 下列哪些关系是对称关系()(2分)A.B.C.D.标准答案:A,D22. 的合取范式为()(2分)A.B.C.D.标准答案:B,D23. 关于复合运算,下列说法正确的是()(2分)A.置换的复合不一定是置换B.置换在复合运算下是封闭的C.可数集的无限子集仍是可数集D.以上说法都正确标准答案:B,C24. 为命题,则下述公式中是重言式为()(2分)A.B.C.D.标准答案:B,D25. 令我上街;我去书店看看;我很累则命题“如果我上街,我就去书店看看,除非我很累”可以符号化为()(2分)A.B.C.D.标准答案:A,D26. 若集合,则()(2分)A.且B.但C.但D.且标准答案:A27. 在()下有。


第一篇 绪论内容:(三句话)典型题例:1、离散数学是计算机科学所涉及的 和 的总称。
2、离散数学是数学中的一个分支,它以 作为其主要研究对象,非常重视 问题的研究。
3、要解决一个问题,首先要证明此问题解的 ,还需要找出得到此问题的步骤来,而且其步骤必须是 ,有规则的,这就是所谓“能行性”问题的研究。
第二篇 集合论内容:典型题例:1、设集合{}{}2,4,3,a B =,那么下列命题中正确的是 。
A 、B a ∈ B 、{}{}B a ⊆4,3,,2C 、{}B a ⊆D 、{}B ⊆φ2、设A ,B 是集合,如果{}}}2,1{,1{,1==B A ,则 。
A 、B A B A ⊆∈且 B 、B A B A ⊄∈但C 、B A B A ⊆∉且D 、B A B A ⊄∉且3、设集合{}{}4,3,,2a A =,那么下列命题中错误的是___。
A 、{}A a ∈ B 、{}{}A a ⊆3,4, C 、{}A a ⊆ D 、A ⊆φ 4、设集合{}Zx x x A ∈<=,3,{}Z k k x x B ∈==,2,{}5,4,3,2,1=C ,则=-+)(B C A 。
A 、{}5,3,1 B 、{}6,4,2 C 、{}8,7,6,0 D 、{}8,7,6,4,2,05、设{}4,3,2,1=A ,{}9,6,4,2=B ,那么集合A ,B 的对称差A+B= 。
A 、{}3,1 B 、{}6,4,2 C 、{}9,6,3,1 D 、{}9,6,4,3,2,1 6、集合{}e d c b a X ,,,,=,X 上的一个划分{}}}{,{},,{e d c b a =π,那么π所对应的等价关系R 应有有 个序偶。
A 、8B 、9C 、10D 、13 7、设集合{}3,2,1=B 上的二元关系{})3,3(),1,1(=R ,则R 不具有___。
A 、传递性B 、自反性C 、对称性D 、反对称性8、设集合{}4,3,2,1=X ,X 上的关系{})4,3(),4,2(),3.2(),1,1(=R ,则R 具有 。



习题 31.集合A={1,{2},3,4},B={a,b,{c}},判定下列各题的正确与错误:(1){1}∈A ; (2){c}∈B ; (3) {1,{2},4}⊆A ;(4){a ,b ,c}⊆B ; (5){2}⊆A ; (6){c}⊆B ; (7)φA ⊂; (8)φ⊆{{2}}⊆A ;(9){φ}⊆B ; (10)φ∈{{2},3}.解:(1)不正确。
因为{1}是集合,集合与集合之间一般不能有属于关系。
(2)正确。
虽然{c}是集合,但是它又是B 中的元素。
(3)正确。
虽然{1,{2},4}是A 的真子集,但是同时满足子集定义,故可以这样表示。
(4)不正确。
因为c ∉B 。
(5)不正确。
虽然{2}是一个集合,但是它只是A 中的一个元素,不能有包含关系。
(6)不正确。
理由同(5)。
(7)正确,符合定义。
(8)正确,都符合定义。
(9)不正确,因为B 中本没有元素φ。
(10)不正确。
φ不是{{2},3}是中的元素,不能有属于关系,若写成φ⊆{{2},3}则可以。
2.求下列集合的幂集:(1) {a ,{b}}; (2) {1,φ}; (3){X ,Y ,Z}解:(1) 设A={a ,{b}},则P(A)={ φ,{a},{{b}},{a ,{b}}}; (2)设B={1,φ},则P(B)= { φ,{1},{φ},{1,φ}};(3)设C={X ,Y ,Z},则P(C)= { φ,{X},{Y},{Z},{X ,Y },{X ,Z },{ Y , Z },{X ,Y ,Z}};3.证明:对任意集合A ,B 都有P(A)∩P(B)=P(A ∩B),P(A)∪P(B)⊆P(A ∪B),并举例说明,一般P(A)∪P(B)≠P(A ∪B)。
证明:对任意的集合C ,若C ∈P(A)∩P(B)⇔C ∈P(A)∧C ∈P(B)⇔C ⊆A ∧C ⊆B ⇔C ⊆A ∩B 所以P(A)∩P(B)=P(A ∩B)成立。
离散数学(高起专)单选题1. 在0_______之间写上正确的符号。
(5分)(A) =(B) (C) (D) 标准答案:D2. 设A={a,{a}},下列命题错误的是_______。
(PA是A的幂集)(5分)(A) {a}PA(B) {a}PA(C) {{a}}PA(D) {{a}}PA标准答案:B3. 设P={x|(x+1)4且x R},Q={x|5x+16且x R},则下列命题哪个正确_______。
(5分)(A) Q P(B) Q P(C) P Q(D) P=Q标准答案:C4. 若A-B=Ф,则下列哪个结论不可能正确?_______(5分)(A) A=Ф(B) B=Ф(C) A B(D) B A标准答案:D5. 永真式的否定是_______(5分)(A) 永真式(B) 永假式(C) 可满足式(D) (1)--(3)均有可能标准答案:B多选题6. 下列公式中哪些是永真式?_______(5分)(A) (┐P Q)→(Q→R)(B) P→(Q→Q)(C) (P Q)→P(D) P→(P Q)标准答案:B,C,D7. 下列命题中,_______是错误的。
(5分)(A) 若A∪B=A∪C,则B=C(B) {a,b}={b,a}(C) P(N∩M)P(N)∩P(M)(P(S)表示S的幂集)(D) 若A为非空集,则A A∪A成立。
标准答案:A,C,D8. 设集合A={2,{a},3,4},B = {{a},3,4,1},E为全集,则下列命题错误的是_______。
(5分)(A) {2}ÎA(B) {a}ÍA(C) ÆÍ{{a}}ÍBÍE(D) {{a},1,3,4}ÌB.标准答案:A,B,D9. 下列命题中正确的是_______。
(5分)(A) {Ф}∈{Ф,{{Ф}}}(B) {Ф}{Ф,{{Ф}}}(C) Ф∈{{Ф}}(D) Ф{Ф}(E) {a,b}∈{a,b,{a},{b}}标准答案:B,D判断题10. 若A È B = A È C,则B = C 。
第5章 等价关系与偏序关系一、选择题(每题3分)1、设Z 为整数集,下面哪个序偶不够成偏序集( A )A 、)(,小于关系:<><<ZB 、)(,小于等于关系:≤>≤<ZC 、,()ZD D <>关系:整除 D 、,()Z M M <>关系:整倍数2、序偶(),A ρ<>⊆必为( B )A 、非偏序集B 、偏序集C 、线序集D 、良序集3、设≤小于等于关系:Z 为整数集,下面哪个序偶能够成良序集( D )A 、,()R R +<>≤:正实数集 B 、,()Q Q ++<≤>有理数集:正 C 、,()Z Z ++<≤>整数集:正 D 、,()N N <≤>:自然数集4、设{,{1},{1,3},{1,2,3}}A =∅,则A 上包含关系“⊆”的哈斯图为( C )5、集合{ 1, 2, 3,4 }A =上的偏序关系图为则它的哈斯图为( A )6、某人有三个儿子,组成集合123{ , , }A S S S =,则在A 上的兄弟关系一定不是( D )A 、偏序关系B 、线序关系C 、良序关系D 、等价关系7、有一个人群集合12{ , ,, }n A P P P =,则在A 上的同事关系一定是( D ) A 、偏序关系 B 、线序关系 C 、良序关系 D 、等价关系8、设A 为非空集合,则下列A 上的二元关系中为等价关系的是( D )A 、空关系B 、全域关系C 、恒等关系D 、上述关系都是9、设{ 1, 2, 3 }A =,则A 上不同等价关系的个数为( C )A 、3B 、4C 、5D 、610、设{ 1, 2, 3, 4 }A =,则A 上不同等价关系的个数为( C )A 、13B 、14C 、15D 、16注:除了等价关系可以对空集定义,而划分不能外,等价关系与划分是相同概念的不同描述.11、设{ 1, 2 }S =,“•”为S 中元素的普通乘法,定义S S ⨯上的等价关系 {,,, | ,,,,}R a b c d a b S S c d S S a d b c =<<><>><>∈⨯<>∈⨯•=•, 则由R 产生的S S ⨯上一个划分的分块数为( D )A 、1B 、2C 、3D 、4提示:记12341,1,1,2,2,1,2,2a a a a =<>=<>=<>=<>,则由R 的关系图易知1234{{},{},{},{}}S S a a a a ⨯=.12、设} 3 ,2 ,1 {=S ,“+”为S 中元素的普通乘法,定义S S ⨯上的等价关系},,,, | ,,,{c b d a S S d c S S b a d c b a R +=+⨯>∈<⨯>∈<><><<=,则由R 产生的S S ⨯上一个划分的分块数为( C )A 、3B 、5C 、7D 、9提示:因a d b c +=+,则a b c d -=-因2,1,0,1,2a b -=--,则等价关系R 产生的S S ⨯上一个划分的分块数为5.二、填充题(每题4分)1、设{ , , , }A a b c d =,其上偏序关系R 的哈斯图为则R = {,,,,,,,,,}A a b a c a d b d c d I <><><><><>.2、设{ , , ,,,, }A a b c d e f g =,偏序集,A R <>的哈斯图为a b c de fg, 则R = {,,,,,,,,,,,,,}A a b a c a d a e a f d f e f I <><><><><><><>.3、偏序集({,}),a b ρ<⊆>的Hass 图为4、对于{ 1,2,3,4,6,8,12,24 }A =,则偏序集,A <>整除关系的哈斯图为1234681224.5、设{ 1,2,3,4,6,8,12,24 }A =,“≤”为A 上整除关系,则偏序集,A <≤>的极小元为1,最小元为1,极大元为24、最大元为24.6、设{ 2,3,4,6,8,12 }A =,“≤”为A 上整除关系,则偏序集,A <≤>的极小元为2,3,最小元为无,极大元为8,12,最大元为无,既非极小元也非极大元的是4,6.7、设},,{c b a A =考虑下列子集}},{},,{{1c b b a S =,}},{},,{},{{2c a b a a S =,}},{},{{3c b a S =,}},,{{4c b a S =,}}{},{},{{5c b a S =,}},{},{{6c a a S = 则A 的覆盖有12345,,,,S S S S S ,A 的划分有345S S S ,,.8、设{ 1, 2, 3,4 }A =,{{1},{2,3},{4}}S =为A 的一个分划,则由S 导出的等价关系为 R = {1,1,2,2,2,3,3,2,3,3,4,4}<><><><><><>.提示:R =({1}{1})({2,3}{2,3})({4}{4})⨯⨯⨯.9、非空正整数子集A 上的模k 等价关系R 的秩为k ,/A R ={[0],[1],,[1]}k k k k -.{}b a ,{}a {}b Φ三、问答题(每题6分)1、试比较偏序集合、线序集合与良序集合.答:若集合A 上的二元关系R 是自反的,反对称的和传递的,称序偶,A R <>为偏序集; 偏序集中的各元素并非都能比较,若都能比较,偏序集成为线序集;在线序集中,若A 的任一非空子集都有一最小元素,则线序集成为良序集.2、设||5A =,R 是A 的等价关系,由R 诱导的A 的划分块数为3,则不同的R 有多少种? 答:一个集合上的等价关系数目与该集合的划分数目是一致的,因而,该题只需求出将5个元素的集合分成3份的划分种数即可.如果3份中元素个数分别为3,1,1,则共有35C 种,如果3份中元素个数分别为2,2,1,则共有25C 种,因此,A 上秩为3的等价关系共有35C +2520C =. 3、设A 是实数集合,试判断{,3}R x y x A y A x y =<>∈∧∈∧-=是A 上的偏序关系吗?等价关系吗?为什么?答:都不是;因 ∀x ∈A ,x -x =0≠2,所以<x ,x >∉R ,R 不是自反的.四、画图填表题(每题10分)1、设{ , , ,,}A a b c d e =上的关系R = {,}A c d I <>,画出偏序集,A R <>的哈斯图, 列表给出A 的子集123{ ,, ,,},{ ,},{,,}B a b c d e B c d B c d e ===的极大元、极小元、最大元、最小元、上界、下界、上确界和下确界.解:哈斯图如图4.44所示:其子集,1,2,3i B i =上的各种特殊元素如下表所示,极大元 极小元 最大元 最小元 上界 下界 上确界 下确界 B 1a ,b ,d ,e a ,b ,c ,e 无 无 无 无 无 无 B 2d c d c d c d c B 3 d ,e c ,e无 无 无 无 无 无 2、设{ , , }A a b c =的幂集()A ρ上的关系⊆= {,()()}x y x A y A x y ρρ<>∈∧∈∧⊆, 画出偏序集(),A ρ<⊆>哈斯图,列表给出()A ρ子1{ ,{},{}}B a b =∅2,{{},{}}B a c =,3{{,},{,,}}B a c a b c =的极大元、极小元、最大元、最小元、上界、下界、上确界和下确界. 解:哈斯图如图4.45所示:其子集,1,2,3i B i =上的各种特殊元素如下表所示,极大元 极小元 最大元 最小元 上界 下界 上确界 下确界 B 1⎨a ⎬,⎨b ⎬ ∅ 无 ∅ ⎨a ,b ,c ⎬, ⎨a ,b ⎬ ∅ ⎨a ,b ⎬ ∅ B 2⎨a ⎬,⎨c ⎬ ⎨a ⎬,⎨c ⎬ 无 无 ⎨a ,b ,c ⎬, ⎨a ,c ⎬ ∅ ⎨a ,c ⎬ ∅ B 3 ⎨a ,b ,c ⎬ ⎨a ,c ⎬ ⎨a ,b ,c ⎬ ⎨a ,c ⎬ ⎨a ,b ,c ⎬ ⎨a ,c ⎬ ⎨a ,b ,c ⎬ ⎨a ,c ⎬3、试填出{1,2,3,4,5}A =上的等价关系R ,其产生划分/{{1,2},{3},{4,5}}A R =,并画出关系图. 解:{1,2}{1,2}{3}{3}{4,5}{4,5}R =⨯⨯⨯其关系图为:六、证明题(每题10分)1、设R 是A 上的二元关系,如果R 是传递的和反自反的,称R 是A 上的拟序关系, 证明:如果R 是A 上的拟序关系,则()A r R R I =是A 上的偏序关系.证明:(1)因()A A r R R I I =⊇,有()r R 是自反的;(2)设,(),x y r R <>∈而x y ≠,则,,x y R <>∈若,,y x R <>∈由R 的传递性,知,,x x R <>∈与R 的反自反性矛盾,则,,y x R <>∉又,,A y x I <>∉有,()A y x R I r R <>∉=,于是有()r R 是反对称的;(3)由R 的传递性,知R R R ⊆,因()()()()(())(())A A A A A r R r R R I R I R I R R I I ==(()())(()())()()A A A A A R R I R R I I I R R R I r R ==⊆,则()r R 可传递; 综上所述,可证()r R 是A 上的偏序关系.2、设R 是A 上的二元关系,如果R 是传递的和反自反的,称R 是A 上的拟序关系, 证明:如果R 是A 上的偏序关系,则A R I -是A 上的拟序关系.证明:(1)()()()A A A A A A R I I R I I R I I R -===∅=∅,则A R I -反自反;(2)设,,,A A x y R I y z R I <>∈-<>∈-,则,,,x y R y z R <>∈<>∈,而,x y y z ≠≠,因R 是传递的,有,x z R <>∈;若x z =,则,,,z y R y z R <>∈<>∈,由R 的反对称性,知y z =,与y z ≠矛盾,于是x z ≠,则,A x z R I <>∈-,有A R I -是传递的; 综上所述,可证A R I -是A 上的拟序关系.3、设R 是A 上的对称和传递关系,证明:若,,,a A b A a b R ∀∈∃∈∂<>∈,则R 是A 上的等价关系.证明:,,,a A b A a b R ∀∈∃∈∂<>∈,因R 是对称的,有,b a R <>∈,又因R 是传递的,所以,a a R <>∈,则R 在A 上自反,故R 是A 上的等价关系.4、设R 是S 上的偏序关系,证明:1R -是S 上的偏序关系.证明:(1)x S ∀∈,因R 在S 上的自反性,则,x x R <>∈,有1,x x R -<>∈,于是,1R -在S 上是自反的;(2)设1,,x y R -<>∈而x y ≠,则,,y x R <>∈因R 在S 上的反对称性,有,,x y R <>∉则1,,y x R -<>∉于是,1R -在S 上是反对称的;(3)设11,,,x y R y z R --<>∈<>∈,则11,,,z y R y x R --<>∈<>∈,因R 在S 上的传递性,有,,z x R <>∈则1,,x z R -<>∈于是,'R 在'S 上是传递的;综上所述,可证1R -是S 上的偏序关系.(题4在证明中用了定义法)5、设R 是S 上的等价关系,证明:1R -是S 上的等价关系.证明:(1)因R 在S 上的自反性,有S I R ⊆,则11S S I I R --=⊆,有1R -在S 上自反; (2)因R 在S 上的对称性,有1R R -=,则111()R R R ---==,有1R -在S 上对称;(3)因R 在S 上的传递性,有2R R ⊆,则1221()R R R R --=⊆=,有1R -在S 上可传递;则2'(')('(''))('')'R R R R S S R S S R ⊆⨯⊆⨯=,有'R 在'S 上是对称的; 综上所述,可证1R -是S 上的等价关系.(题5在证明中用了集合法)6、设,R S 是A 上的偏序关系,证明:R S 是A 上的偏序关系.证明:(1)x A ∀∈,因,R S 在A 上的自反性,则,x x R S <>∈,有R S 在A 上自反;(2)设,,x y R S <>∈而x y ≠,则,,,,x y R x y S <>∈<>∈因,R S 在A 上的反对称性,有,,,,y x R y x S <>∉<>∉则,,y x R S <>∉于是,R S 在A 上是反对称的;(3)设,,,x y R S y z R S <>∈<>∈,则,,,;,,,x y R y z R x y S y z S <>∈<>∈<>∈<>∈,因,R S 在A 上的传递性, 有,,,x z R x z S <>∈<>∈,则,x z R S <>∈,于是,R S 在A 上是传递的; 综上所述,可证R S 是A 上的偏序关系.(题6在证明中用了定义法)7、设,R S 是A 上的等价关系,证明:R S 是A 上的等价关系.证明:(1)因,R S 在A 上自反,有,A A I R I S ⊆⊆,则A I R S ⊆,有R S 在A 上自反;(2)因,R S 在A 上对称,有11,RR S S --==, 则111()R S R S R S ---==,有R S 在A 上对称;(3)因,R S 在A 上传递,有22,R R S S ⊆⊆,则222()(())(())R S R S R R S S RS R S ⊆⊆⊆,有R S 在A 上可传递; 综上所述,可证R S 是A 上的等价关系.(题7在证明中用了集合法)8、设R 是S 上的二元关系,'S S ⊆定义'S 上的二元关系'('')R R S S =⨯,证明:如果R 是S 上的偏序关系,那么'R 是'S 上的偏序关系.证明:(1)'x S S ∀∈⊆,因R 在S 上的自反性,则,x x R <>∈,而,''x x S S <>∈⨯, 有,('')'x x R S S R <>∈⨯=,于是,'R 在'S 上是自反的;(2)设,',x y R <>∈而x y ≠,则,,x y R <>∈因R 在S 上的反对称性,有,,y x R <>∉ 则,('')',y x R S S R <>∉⨯=于是,'R 在'S 上是反对称的;(3)设,',,'x y R y z R <>∈<>∈,因R 在S 上的传递性,有,,x z R <>∈而,''x z S S <>∈⨯,则,('')'x z R S S R <>∈⨯=,于是,'R 在'S 上是传递的; 综上所述,可证'R 是'S 上的偏序关系.(题8在证明中用了定义法)9、设R 是S 上的二元关系,'S S ⊆定义'S 上的二元关系'('')R R S S =⨯,证明:如果R 是S 上的等价关系,那么'R 是'S 上的等价关系.证明:(1)因R 在S 上的自反性,则S I R ⊆,而'S S ⊆,有'S S I I R ⊆⊆,而'''S I S S ⊆⨯, 有'('')'S I R S S R ⊆⨯=,于是,'R 在'S 上是自反的;(2)因R 在S 上的对称性,有1RR -=,而1('')''S S S S -⨯=⨯, 则1111(')((''))('')'R R S S R S S R ----=⨯=⨯=,有'R 在'S 上是对称的; (3)因R 在S 上的传递性,有2R R ⊆, 有2'R R R R ⊆⊆,而2'('')('')''R S S S S S S ⨯⊆⨯=⨯,则2'(')('(''))('')'R R R R S S R S S R ⊆⨯⊆⨯=,有'R 在'S 上是传递的; 综上所述,可证'R 是'S 上的等价关系.(题9在证明中用了集合法)10、若R 是A 上的等价关系,则{,|,(,,)}S a b a b A c A a c R c b R =<>∈∧∃∈<>∈∧<>∈也是A 上的一个等价关系.证明:(1)A a ∈∀,由R 自反,则,,a a R a a R <>∈∧<>∈,S a a >∈∴<,,有S 自反;(2),a b S ∀<>∈,则c A ∃∈,使,,,,a c R c b R <>∈<>∈由R 在A 上对称,有,,,,b c R c a R <>∈<>∈有,b a S <>∈,知S 对称;(3)若,,,a b S b c S <>∈<>∈,则d A ∃∈,使,,,,a d R d b R <>∈<>∈同时e A ∃∈,使,,,,b e R e c R <>∈<>∈由R 在A 上传递,知,,,,a b R b c R <>∈<>∈有,a c S <>∈,有S 传递;综上所述,可证S 是A 上的等价关系.(题10在证明中用了定义法)六、证明计算题(每题10分)1、设{1,2,3}A =,在A A ⨯上定义:,,,R a b c d R <<><>>∈⇔ a b c d +=+, “+”为普通加法,证明:R 是A A ⨯上的等价关系,并求出[1,3],/R A A R <>⨯. 证明:(1),,,,,,,a b A A a b a b a b a b R ∀<>∈⨯+=+∴<<><>>∈即R 自反;(2),,,,,,a b c d R a b c d c d a b ∀<<><>>∈+=++=+∴则则,,,c d a b R <<><>>∈,即R 对称;(3),,,,,,,,a b c d R c d e f R ∀<<><>>∈<<><>>∈a b c d e f +=+=+则, ,,,,a b e f R ∴<<><>>∈即R 传递;综上得出,R 是A A ⨯上的等价关系,且[1,3]R <>{,,,4}{1,3,2,2,3,1}a b a b A A a b =<><>∈⨯+==<><><>, /{[1,1],[1,2],[1,3],[2,3],[3,3]}R R R R R A A R ⨯=<><><><><>.2、设{1,2,3,4}A =,在A A ⨯上定义:,,,R a b c d R <<><>>∈⇔ c b d a +=+, “+”为普通加法,证明:R 是A A ⨯上的等价关系,并求出[2,4],/R A A R <>⨯. 证明:(1),,,,,,,a b A A a b b a a b a b R ∀<>∈⨯+=+∴<<><>>∈即R 自反;(2),,,,,,a b c d R a d b c c b d a ∀<<><>>∈+=++=+∴则则,,,c d a b R <<><>>∈,即R 对称;(3),,,,,,,,a b c d R c d e f R ∀<<><>>∈<<><>>∈,a d b c c f d e a d c f b c d e +=++=++++=+++∴则有 a f b e +=+,,,,,a b e f R ∴<<><>>∈即R 传递;综上得出,R 是A A ⨯上的等价关系,且[2,4]R <>{,,,2}{1,3,2,4}a b a b A A a b =<><>∈⨯=-=<><>,/{[1,1],[1,2],[2,1],[1,3],[3,1],[1,4],[4,1]}R R R R R R R A A R ⨯=<><><><><><><>.3、设{1,2,3,4}A =,在A A ⨯上定义:,,,R a b c d R <<><>>∈⇔ a d b c =, “” 为普通乘法,证明: R 是A A ⨯上的等价关系,并求出[2,4],/R A A R <>⨯. 证明:(1),,,,,,,a b A A a b b a a b a b R ∀<>∈⨯=∴<<><>>∈即R 自反;(2),,,,,,a b c d R a d b c c b d a ∀<<><>>∈==∴则则,,,c d a b R <<><>>∈,即R 对称;(3),,,,,,,,a b c d R c d e f R ∀<<><>>∈<<><>>∈,a d b c c f d e a d c f b c d e ===∴则,有 a f b e =,,,,,a b e f R ∴<<><>>∈即R 传递;综上得出,R 是A A ⨯上的等价关系,且[2,4]R <>{,,,2}{1,2,2,4}a b a b A A a b =<><>∈⨯==<><>,/{[1,1],[1,2],[2,1][1,3],[3,1],[1,4],[4,1]}R R R R R R R A A R ⨯=<><><><><><><>.4、设{ 1, 2, 3, 4 }A =,在A 的幂集()A ρ上规定{,|,()(||||}R s t s t A s t ρ=<>∈∧=, 证明:R 是()A ρ上的等价关系,并写出商集()A R ρ.证明:⑴()s A ρ∀∈ ,由于||||s s =,所以R s s >∈<,,即R 自反的;⑵,()s t A ρ∀∈ ,若R t s >∈<,,则||||||||s t t s =⇒=,R s t >∈∴<,,R 是对称的; ⑶,,()s t u A ρ∀∈,若R u t R t s >∈<>∈<,,且,即||||||u t s ==,则,s u R <>∈ 所以R 是传递的;综上得出,R 是()A ρ上的等价关系,(){[],[{1}],[{1,2}],[{1,2,3}],[{1,2,3,4}]}R R R R R A R ρ=∅.。