最新北师大版初中八年级数学上册中考数学复习专题3:二元一次方程(组)
- 格式:doc
- 大小:1.30 MB
- 文档页数:34

专题5.1认识二元一次方程组(知识梳理与考点分类讲解)【知识点1】二元一次方程1.定义含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.2.二元一次方程的条件(1)整式方程;(2)只含有两个未知数;3.关于x,y的两元一次方程的一般形式:ax+by=c(a≠0,b≠0).特别提醒:“所含未知数的项的次数都是1”不可理解为两个未知数的次数都是1,例如2xy+1=0不是二元一次方程.【知识点2】二元一次方程组1.定义共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.2.二元一次方程组应满足的条件:(1)两个方程都是整式方程;(2)共含有两个未知数;(3)两个方程都是一次方程;特别提醒:判断二元一次方程组时,误认为每个方程必须是二元一次方程.【知识点3】二元一次方程的解1.二元一次方程组的解适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解.2.判断一对数值是不是二元一次方程的解的方法:判断一对数值是不是二元一次方程的解,只需将这对数值分别代入方程的左右两边,看其是否相等.特别提醒:二元一次方程只要给定其中的一个未知数的值,就可以相应地求出另一个未知数的值,因此二元一次方程有无数个解.二元一次方程的整数解有时只有有限个.【知识点4】二元一次方程组的解1.二元一次方程组的解二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.2.判断一对数值是不是二元一次方程组的解的方法判断一对数值是否为一个二元一次方程组的解,必须将这对数值分别带入方程组中的每一个方程进行检验,若满足没一个方程,则这对数值就是这个方程组的解,否则就不是这个方程组的解.特别提醒:方程组的解一定是方程组中每个方程的解,而方程组中某个方程的解不一定是方程组的解.【考点目录】【考点1】二元一次方程的认识;【考点2】二元一次方程组的认识【考点3】二元一次方程的解;【考点4】二元一次方程组的解【答案】0【分析】根据二元一次方程的定义:含有两个未知数,并且所含未知数的项的次数都是1的整式方程,进行求解即可解:∵方程()()33420m n m xn y --+--=是关于x y ,的二元一次方程,∴40312031m m n n +≠⎧⎪-=⎪⎨-≠⎪⎪-=⎩,∴44m n ==,,∴m n -440=-=【点拨】本题考查二元一次方程的定义,掌握二元一次方程组的定义是解题关键.二元一次方程需满足三个条件:①首先是整式方程.②方程中共含有两个未知数.③所有未知项的次数都是一次.【举一反三】【变式1】(2023上·河北张家口·八年级统考期中)下列是二元一次方程的是()A .215x -=B .21x y +=C .23x y +=D .12y x+=【答案】C【分析】本题考查了二元一次方程的定义,二元一次方程需满足三个条件:①首先是整式方程,②方程中共含有两个未知数,③所有未知项的次数都是一次,不符合上述任何一个条件的都不叫二元一次方程.解:A .215x -=,是一元一次方程,故本选项不符合题意;B .21x y +=,是二元二次方程,故本选项不符合题意;C .23x y +=,是二元一次方程,故本选项符合题意;D .12y x+=,是分式方程,故本选项不符合题意.故选:C .【变式2】(2022下·湖北荆州·七年级校考期中)若方程:223m x ++514n y -=6是关于x 、y 的二元一次方程,则n m -的平方根为.【答案】2±【分析】根据二元一次方程的定义,得各个未知数的次数为1,求得m ,n 的值,进而求解.解:由题意,得:231m +=,5141n -=,解得1m =-,3n =.∴()314n m -=--=,∴n m -的平方根2=±.故答案为:2±.【点拨】本题考查二元一次方程的定义,平方根,熟练掌握只含有两个未知数,且未知项的次数为1的整式方程是二元一次方程是解题的关键.【考点二】二元一次方程组的认识【例2】(2017下·四川宜宾·七年级校联考阶段练习)已知方程组()()2233112m x m ym x --⎧--=⎪⎨+=-⎪⎩是二元一次方程组,求m 的值.【答案】m =5解:依题意,得:|m -2|-2=1,且m -3≠0,且m +1≠0,解得:m =5.【点拨】本题考查了二元一次方程组的定义.二元一次方程组也满足三个条件:①方程组中的两个方程都是整式方程,②方程组中共含有两个未知数,③每个方程都是一次方程.【举一反三】【变式1】(2023下·河北廊坊·七年级统考期末)下列方程组中是二元一次方程组的是()A .436231x y y z -=⎧⎨-=⎩B .45342x y x =⎧⎨-=⎩C .46323xy x y =⎧⎨+=⎩D .23325y xy x ⎧+=⎪⎨⎪+=⎩【答案】B【分析】根据二元一次方程组定义判断即可.解: A.此方程组含有,,x y z 三个未知数,故不是二元一次方程组,故此选项不符合题意;B .该方程组是二元一次方程组,故此选项符合题意;C .46xy =是二元二次方程,故不是二元一次方程组,故此选项不符合题意;D .233y x+=是分式方程,故不是二元一次方程组,故此选项不符合题意;故选:B .【点拨】本题主要考查了二元一次方程的定义.一定要紧扣二元一次方程组的定义回答.【变式2】(2023下·江苏徐州·七年级统考期末)观察所给的4个方程组:①23x y =⎧⎨=⎩;②415343x y x =⎧⎨-=-⎩;③2164x y x y +=⎧⎨-=⎩;④352494x y x y +=⎧⎨+=⎩,其中,符合二元一次方程组定义的是(写出所有正确的序号).【答案】①②④【分析】含有两个未知数,且未知数的最高次数是1,这样的整式方程组是二元一次方程组,根据定义逐一判断即可.解:①23x y =⎧⎨=⎩,符合二元一次方程组定义;②415343x y x =⎧⎨-=-⎩,符合二元一次方程组定义;③2164x y x y +=⎧⎨-=⎩,未知数x 的最高次数是2,不符合二元一次方程组定义;④352494x y x y +=⎧⎨+=⎩,符合二元一次方程组定义;所以符合二元一次方程组定义的是①②④.故答案为:①②④.【点拨】本题考查的是二元一次方程组的定义,熟记定义是解本题的关键.【考点三】二元一次方程的解【例3】(2023上·河北张家口·八年级统考期中)已知24x y =⎧⎨=⎩是关于x ,y 的二元一次方程314x ay +=的一组解.(1)求a 的值(2)请用含有x 的代数式表示y .【答案】(1)2a =;(2)372y x=-【分析】(1)将二元一次方程的解24x y =⎧⎨=⎩代入314x ay +=得到关于a 的方程,解关于a 的方程即可;(2)将2a =代入314x ay +=得到3214x y +=,将x 看作已知数,y 看作未知数,解关于y 的方程即可.(1)解:将24x y =⎧⎨=⎩代入314x ay +=,得:32414a ⨯+=,解得2a =;(2)解:∵2a =,∴原方程可变为3214x y +=,∴372y x =-.【举一反三】【变式1】(2023上·陕西西安·八年级高新一中校考期中)若关于x 、y 的二元一次方程221x y a +=-的一组解为3x =,1y =,则a 的值是()A .3B .2C .1D .1-【答案】A【分析】本题考查了二元一次方程的解,解题的关键是掌握二元一次方程的定义.把3x =,1y =代入到221x y a +=-中即可求解.解:把3x =,1y =代入到221x y a +=-中得:21321a -=+⨯,216a -=,3a =,故选:A .【变式2】(2023上·全国·八年级专题练习)小方解方程组232ax by cx y +=⎧⎨-=-⎩时,因抄错了a ,解得11x y =⎧⎨=⎩,则c 的值为.【答案】1【分析】本题主要考查了二元一次方程的解,将解代入第二个方程即可解答.解:把11x y =⎧⎨=⎩代入32cx y -=-得:32c -=-,解得:1c =.故答案为:1.【考点四】二元一次方程组的解【例4】(2023上·全国·八年级专题练习)甲和乙两人同解方程组125bx y x ay +=⎧⎨+=⎩,甲因抄错了a ,解得52x y =⎧⎨=⎩,乙因抄错了b ,解得32x y =⎧⎨=⎩,求52a b -的值.【答案】1【分析】本题考查了二元一次方程组的解,将甲、乙求得的解分别代入正确的方程,求出a ,b 的值即可求解,用代入法解方程是解本题关键.解:由题意52x y =⎧⎨=⎩,是12bx y +=的解,∴5212b +=,解得2b =,又 32x y =⎧⎨=⎩是5x ay +=的解,∴325a +=,解得1a =,5251221a b ∴-=⨯-⨯=.【举一反三】【变式1】(2023上·广东深圳·八年级校联考期中)若关于x ,y 的二元一次方程组2138x ay bx y -=-⎧⎨+=⎩的解是15x y =⎧⎨=⎩,则关于m 、n 的二元一次方程组()()()()2138m n a m n b m n m n ⎧+--=-⎪⎨++-=⎪⎩的解是()A .15m n =⎧⎨=⎩B .51m n =⎧⎨=⎩C .23m n =-⎧⎨=⎩D .32m n =⎧⎨=-⎩【答案】D【分析】本题考查了二元一次方程组的解及解二元一次方程组,先将15x y =⎧⎨=⎩代入2138x ay bx y -=-⎧⎨+=⎩解得357a b ⎧=⎪⎨⎪=-⎩,再将357a b ⎧=⎪⎨⎪=-⎩代入()()()()2138m n a m n b m n m n ⎧+--=-⎪⎨++-=⎪⎩即可求解,熟练掌握二元一次方程组的解及利用加减消元法解二元一次方程组是解题的关键.解:将15x y =⎧⎨=⎩代入2138x ay bx y -=-⎧⎨+=⎩得:251158a b -=-⎧⎨+=⎩,解得:357a b ⎧=⎪⎨⎪=-⎩,()()()()3215738m n m n m n m n ⎧+--=-⎪∴⎨⎪-++-=⎩,解得:32m n =⎧⎨=-⎩,故选D .【变式2】(2023下·七年级单元测试)写出一个解为25x y =⎧⎨=-⎩的二元一次方程组:.【答案】37x y x y +=-⎧⎨-=⎩(答案不唯一)【分析】方程组的解,指的是该数值满足方程组中的每一方程.在求解时,应先围绕25x y =⎧⎨=-⎩列一组算式,如253-=-,257+=,然后用x ,y 代换,可得方程组.解:先围绕25x y =⎧⎨=-⎩列一组算式,如:253-=-,257+=,然后用x ,y 代换,可得37x y x y +=-⎧⎨-=⎩等.答案不唯一,符合题意即可.故答案为:37x y x y +=-⎧⎨-=⎩(答案不唯一).【点拨】本题考查二元一次方程组的解,此题是开放性题目,答案不唯一.掌握二元一次方程组解的意义是解题的关键.。



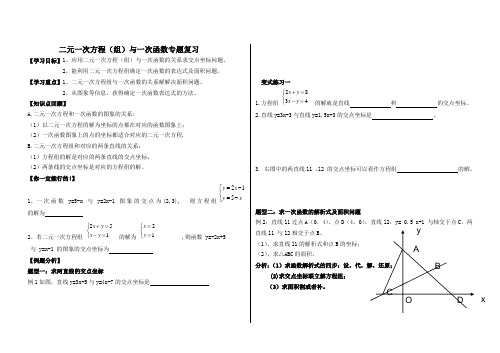
二元一次方程(组)与一次函数专题复习【学习目标】1、应用二元一次方程(组)与一次函数的关系求交点坐标问题。
2、能利用二元一次方程组确定一次函数的表达式及面积问题。
【学习重点】1、二元一次方程组与一次函数的关系解解决面积问题。
2、从图象等信息,获得确定一次函数表达式的方法。
【知识点回顾】A.二元一次方程和一次函数的图象的关系:(1)以二元一次方程的解为坐标的点都在对应的函数图象上; (2)一次函数图象上的点的坐标都适合对应的二元一次方程. B.二元一次方程组和对应的两条直线的关系: (1)方程组的解是对应的两条直线的交点坐标; (2)两条线的交点坐标是对应的方程组的解。
【你一定能行的!】1、一次函数y=5-x 与y=2x-1图象的交点为(2,3), 则方程组⎩⎨⎧-=-=x y x y 512的解为2、若二元一次方程组 ⎩⎨⎧=-=+152y x y x 的解为 ⎩⎨⎧==12y x ,则函数 y=-2x+5 与 y=x-1 的图象的交点坐标为 【例题分析】题型一:求两直线的交点坐标例1如图,直线y=3x+5与y=4x-7的交点坐标是变式练习一1.方程组 ⎩⎨⎧=-=+4382y x y x 的解就是直线 和 的交点坐标。
2.直线y=3x-3与直线y=1.5x+3的交点坐标是 。
3. 右图中的两直线l1 ,l2 的交点坐标可以看作方程组 的解。
题型二:求一次函数的解析式及面积问题例2:直线l1过点A (0,4),点D (4,0),直线l2:y= 0.5 x+1 与轴交于点C ,两直线l1 与l2相交于点B 。
(1)、求直线l1的解析式和点B 的坐标; (2)、求△ABC 的面积。
分析:(1(2)求交点坐标联立解方程组; (3)求面积割或者补。
x变式练习二1.求两条直线y=3x-2与y=-2x+4和x轴所围成的三角形的面积.(你能求出这两条直线与y轴所围成的三角形的面积吗?)2.已知:函数y = (m+1) x+2 m﹣6(1)若函数图象过(﹣1 ,2),求此函数的解析式。

1数学八年级二元一次方程组专题复习■专题一:二元一次方程(组)有关概念 1、二元一次方程(组)的识别二元一次方程组是指含有_______未知数,且含未知数的项的次数是_______的方程组。
例1 下列方程组是二元一次方程组的是( )A 、23x y y z +=⎧⎨+=⎩;B 、2325x y x y ⎧=⎪⎨⎪+=⎩;C 、226y x y =⎧⎨-=⎩;D 、236x y xy +=⎧⎨=⎩。
2、方程组的解例2 方程组379475x y x y +=⎧⎨-=⎩的解是( ) A .21x y =-⎧⎨=⎩ ;B .237x y =-⎧⎪⎨=⎪⎩;C .237x y =⎧⎪⎨=-⎪⎩;D .237x y =⎧⎪⎨=⎪⎩。
■专题二:利用二元一次方程组求字母系数的值 例1. 若单项式22mx y 与313n x y -是同类项,则m n +的值是 . 例2.解方程组51542ax y x by +=⎧⎨-=-⎩时,甲由于看错系数a ,结果解得31x y =-⎧⎨=-⎩;乙由于看错系数b ,结果解得54x y =⎧⎨=⎩,则原来的a=______,b=______. 练习:1、若22(1)0m n ++-=,则2m n +的值为( )A .4-B .1-C .0D .4。
2、若2a bxy +与231a x y +是同类项,则a -b 的值等于______.3、如果关于x 、y 的方程组27282x y kx y k+=+⎧⎨-=-⎩的解满足3x+y=5,求k 的值。
4、如果关于x 、y 的方程组62x y ax y b -=⎧⎨+=⎩的解与38x ay x y +=⎧⎨+=⎩的解相同,求a 、b 的值。
■专题三:解二元一次方程组1、求二元一次方程的整数解。
例1 求方程2x+5y=50的所有正整数解。
点评:二元一次方程又称不定方程,意思是说它有不确定的解,但对于特殊的解(如正整数解、负整数解等)或在某些条件下的解往往是有限的。
北师大版八年级数学上册(二元一次方程组)知识点总结北师大版八年级数学上册(二元一次方程组)知识点总结第五章二元一次方程组1、二元一次方程含有两个未知数,并且所含未知数的项的次数都是1的整式方程叫做二元一次方程。
2、二元一次方程的解合适一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解。
3、二元一次方程组含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组。
4二元一次方程组的解二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解。
5、二元一次方程组的解法〔1〕代入〔消元〕法:将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,这种解方程的方法称为代入消元法,简称代入法。
〔2〕加减〔消元〕法:通过两式相加〔减〕消去其中一个未知数,这种解二元一次方程组的方法叫做加减消元法,简称加减法。
6、一次函数与二元一次方程〔组〕的关系:〔1〕一次函数与二元一次方程的关第五章二元一次方程组1、二元一次方程含有两个未知数,并且所含未知数的项的次数都是1的整式方程叫做二元一次方程。
2、二元一次方程的解合适一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解。
3、二元一次方程组含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组。
4二元一次方程组的解二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解。
5、二元一次方程组的解法〔1〕代入〔消元〕法:将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,这种解方程的方法称为代入消元法,简称代入法。
〔2〕加减〔消元〕法:通过两式相加〔减〕消去其中一个未知数,这种解二元一次方程组的方法叫做加减消元法,简称加减法。
6、一次函数与二元一次方程〔组〕的关系:〔1〕一次函数与二元一次方程的关系:直线y=kx+b上任意一点的坐标都是它所对应的二元一次方程kx- y+b=0的解。
学易佳教育中心八年级上册第五章二元一次方程组基础知识1.二元一次方程具有两个未知数, 并且所含未知数旳项旳次数都是1旳整式方程叫做二元一次方程。
2.二元一次方程旳解适合一种二元一次方程旳一组未知数旳值, 叫做这个二元一次方程旳一种解。
3.二元一次方程组具有两个未知数旳两个一次方程所构成旳一组方程, 叫做二元一次方程组。
4二元一次方程组旳解二元一次方程组中各个方程旳公共解, 叫做这个二元一次方程组旳解。
5.二元一次方程组旳解法(1)代入(消元)法(2)加减(消元)法6.一次函数与二元一次方程(组)旳关系:(1)一次函数与二元一次方程旳关系:直线y=kx+b上任意一点旳坐标都是它所对应旳二元一次方程kx- y+b=0旳解(2)一次函数与二元一次方程组旳关系:二元一次方程组 旳解可看作两个一次函数和 旳图象旳交点。
当函数图象有交点时, 阐明对应旳二元一次方程组有解;当函数图象(直线)平行即无交点时, 阐明对应旳二元一次方程组无解。
【基础训练】1.下列方程是二元一次方程旳有: ___________________(只填序号)①093=-+y x ②012232=+-y x ③202=+y x ④113=-yx ⑤3A-4B=70 ⑥x 2+10=02.甲种物品每个4kg, 乙种物品每个7kg 。
既有甲种物品x 个, 乙种物品y 个, 共76kg.(1)列出有关x,y 旳二元一次方程组_____________________________(2)若x=12,则y=___________(3)若有乙种物品8个, 则甲种物品有_________个。
3、小明从邮局买了面值50分和80分旳邮票共9枚, 花了6.3元, 小明买了50分邮票枚, 买了80分邮票枚, 则根据题意可列方程组:___________________⎩⎨⎧=+=+222111c y b x a c y b x a 22122b c x b a y +-=4.、下列四组数值中, 哪些是二元一次方程旳解_______________(1)⎩⎨⎧=-=;6,2y x (2)⎩⎨⎧==;4,3y x (3)⎩⎨⎧==;3,4y x (4)⎩⎨⎧-==.2,6y x 5.、二元一次方程组旳解是( )(A )⎩⎨⎧==;3,4y x (B )⎩⎨⎧==;6,3y x (C )⎩⎨⎧==;4,2y x(D )⎩⎨⎧==.2,4y x 6.用代入消元法解下列方程组:1. 2、7、用加减消元法解下列方程组:1. 2、3. 4.【巩固提高】一、填空题:1. 已知/是有关x,y 旳二元一次方程, 则m = .2.假如/是一种二元一次方程, 那么数/= , /= .3.假如/是同类项, 那么 /= , /= .4.请写出方程x+2y=7旳一种正整数解是 .5./中, 若/则/_______.6.由/_______, /_______.7.假如那么_______. 8. 已知二元一次方程/当/时, y = .9. /是二元一次方程2x +by =-2旳一种解, 则b 旳值等于 .10. 已知/和/都是ax +by =7旳解, 则a = , b = .11. 已知/, 则x +y = .12. 若方程组/旳解是/, 则/.13. 某年级有学生246人, 其中男生比女生人数旳2倍少3人, 问男女学生各多少人, 设女生人数为x 人, 男生人数为y 人, 可列方程组为 .⎩⎨⎧=-=+.232,12y x y x =-+-+3962242y x y x14.购面值各为20分, 30分旳邮票共27枚, 用款6.6元。
北师大版八年级上册数学单元复习高频考点整合练二元一次方程组高频考点一:二元一次方程(组)及其解法1.方程组的解是( )A. B. C. D.2. 下列是二元一次方程的是( )A.x-yB.x+y-m=0C.+3=0D.x-2y=13.方程组的解是 __.4. 写出二元一次方程x+y=6的一组整数解为__.5.解方程组6.解方程组高频考点二:二元一次方程组与一次函数的关系1 / 51.某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )A.9:15B.9:20C.9:25D.9:302. 若关于x,y的二元一次方程组的解为,一次函数y=kx+b 与y=mx+n的图象的交点坐标为( )A.(1,2)B.(2,1)C.(2,3)D.(1,3)3.如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的表达式是_ _.4.在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是 __.5.安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:(1)求y与x之间的函数表达式.(2)商贸公司要想获利2 090元,则这种干果每千克应降价多少元?6. 某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费,如图表示了公司每月付给推销员推销费的两种方案,看图解答下列问题:(1)求y1与y2的函数表达式.(2)解释图中表示的两种方案是如何付推销费的..(3)如果你是推销员,应如何选择付费方案3 / 51.《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺.将绳子对折再量长木,长木还剩余1尺,问木长多少尺,现设绳长x尺,木长y尺,则可列二元一次方程组为( )A. B.C. D.2.某水果商从批发市场用8 000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.大樱桃和小樱桃的进价分别是每千克多少元?3.小甘到文具超市去买文具.请你根据图中的对话信息,求中性笔和笔记本的单价分别是多少元?4.亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?(2)若同时调配 36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?5 / 5。
专题07 二元一次方程(组)☞解读考点☞2年中考【2015年题组】1.(2015巴中)若单项式22a bx y+与413a bx y--是同类项,则a,b的值分别为()A.a=3,b=1 B.a=﹣3,b=1 C.a=3,b=﹣1 D.a=﹣3,b=﹣1 【答案】A.【解析】试题分析:∵单项式22a bx y +与413a b x y --是同类项,∴24a b a b -=⎧⎨+=⎩,解得:a=3,b=1,故选A .考点:1.解二元一次方程组;2.同类项.2.(2015广元)一副三角板按如图方式摆放,且∠1比∠2大50°,若设∠1=x°, ∠2=y°.则可得到的方程组为( )A .50180x y x y =-⎧⎨+=⎩B .50180x y x y =+⎧⎨+=⎩C .5090x y x y =-⎧⎨+=⎩D .5090x y x y =+⎧⎨+=⎩【答案】D .考点:1.由实际问题抽象出二元一次方程组;2.余角和补角. 3.(201510b -+=,则()2015b a -=( )A .﹣1B .1C .20155 D .20155-【答案】A . 【解析】试题分析:∵10b -+=,∴⎩⎨⎧=+-=++01205b a b a ,解得:⎩⎨⎧-=-=32b a ,则()20152015321b a -=-+=-().故选A .考点:1.解二元一次方程组;2.非负数的性质.4.(2015内江)植树节这天有20名同学共种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵.设男生有x人,女生有y人,根据题意,下列方程组正确的是()A.52 3220 x yx y+=⎧⎨+=⎩ B.52 2320 x yx y+=⎧⎨+=⎩ C.20 2352 x yx y+=⎧⎨+=⎩ D.20 3252 x yx y+=⎧⎨+=⎩【答案】D.【解析】试题分析:设男生有x人,女生有y人,根据题意可得:203252x yx y+=⎧⎨+=⎩,故选D.考点:由实际问题抽象出二元一次方程组.5.(2015乐山)电影《刘三姐》中,秀才和刘三姐对歌的场面十分精彩.罗秀才唱到:“三百条狗交给你,一少三多四下分,不要双数要单数,看你怎样分得均?”刘三姐示意舟妹来答,舟妹唱道:“九十九条打猎去,九十九条看羊来,九十九条守门口,剩下三条财主请来当奴才.”若用数学方法解决罗秀才提出的问题,设“一少”的狗有x条,“三多”的狗有y条,则解此问题所列关系式正确的是()A.33000300x yx y+=⎧⎨<<<⎩B.33000300x yx yx y+=⎧⎪<<<⎨⎪⎩、为奇数C.330003300x yx yx y+=⎧⎪<=<⎨⎪⎩、为奇数D.3300 0300 0300 x yxyx y+=⎧⎪<<⎪⎨<<⎪⎪⎩、为奇数【答案】B.考点:由实际问题抽象出二元一次方程.6.(2015龙东)为推进课改,王老师把班级里40名学生分成若干小组,每小组只能是5人或6人,则有几种分组方案( ) A .4 B .3 C .2 D .1 【答案】C . 【解析】试题分析:设5人一组的有x 个,6人一组的有y 个,根据题意可得:5x+6y=40,当x=1,则y=356(不合题意);当x=2,则y=5;当x=3,则y=256(不合题意);当x=4,则y=103(不合题意);当x=5,则y=52(不合题意);当x=6,则y=53(不合题意);当x=7,则y=56(不合题意);当x=8,则y=0;故有2种分组方案.故选C .考点:二元一次方程的应用.7.(2015淄博)已知21x y =⎧⎨=⎩是二元一次方程组81mx ny nx my +=⎧⎨-=⎩的解,则2m n -的平方根为( )AC. D .2 【答案】A . 【解析】试题分析:∵将21x y =⎧⎨=⎩代入81mx ny nx my +=⎧⎨-=⎩中,得:2821m n n m +=⎧⎨-=⎩,解得:32m n =⎧⎨=⎩,∴2m ﹣n=6﹣2=4,则2m ﹣n 的平方根为±2.故选A . 考点:1.二元一次方程组的解;2.平方根;3.综合题.8.(2015南充)已知关于x ,y 的二元一次方程组⎩⎨⎧-=+=+12,32y x k y x 的解互为相反数,则k 的值是 . 【答案】﹣1.考点:二元一次方程组的解.9.(2015咸宁)如果实数x,y满足方程组12225x yx y⎧-=-⎪⎨⎪+=⎩,则22x y-的值为.【答案】54-.【解析】试题分析:方程组第二个方程变形得:2(x+y)=5,即x+y=52,∵x﹣y=12-,∴原式=(x+y)(x﹣y)=54-,故答案为:54-.考点:1.解二元一次方程组;2.平方差公式.10.(2015武汉)定义运算“*”,规定x*y=2ax by+,其中a、b为常数,且1*2=5,2*1=6,则2*3= .【答案】10.【解析】试题分析:根据题中的新定义化简已知等式得:2546a ba b+=⎧⎨+=⎩,解得:a=1,b=2,则2*3=4a+3b=4+6=10,故答案为:10.考点:1.解二元一次方程组;2.新定义;3.阅读型.11.(2015北京市)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?”设每头牛值金x 两,每只羊值金y 两,可列方程组为 .【答案】5210258x y x y +=⎧⎨+=⎩.考点:由实际问题抽象出二元一次方程组. 12.(2015庆阳)若22m nx y --与423m n x y +是同类项,则3m n -的立方根是 .【答案】2. 【解析】试题分析:若22m n x y --与423m nx y +是同类项,则:422m n m n -=⎧⎨+=⎩,解方程得:22m n =⎧⎨=-⎩.∴3m n -=2﹣3×(﹣2)=8.8的立方根是2.故答案为:2. 考点:1.立方根;2.合并同类项;3.解二元一次方程组;4.综合题. 13.(2015滨州)某服装厂专门安排210名工人进行手工衬衣的缝制,每件衬衣由2个小袖、1个衣身、1个衣领组成,如果每人每天能够缝制衣袖10个,或衣身15个,或衣领12个,那么应该安排 名工人缝制衣袖,才能使每天缝制出的衣袖,衣身、衣领正好配套. 【答案】120. 【解析】试题分析:设应该安排x 名工人缝制衣袖,y 名工人缝制衣身,z 名工人缝制衣领,才能使每天缝制出的衣袖,衣身、衣领正好配套,依题意有:21010:15:122:1:1x y z x y z ++=⎧⎨=⎩,解得:1204050x y z =⎧⎪=⎨⎪=⎩.故应该安排120名工人缝制衣袖,才能使每天缝制出的衣袖,衣身、衣领正好配套.故答案为:120. 考点:三元一次方程组的应用.14.(2015北海)某市居民用电的电价实行阶梯收费,收费标准如下表:(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a ,b 的值.(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度? 【答案】(1)0.61,0.66;(2)450.考点:1.一元一次不等式的应用;2.二元一次方程组的应用.15.(2015南通)由大小两种货车,3辆大车与4辆小车一次可以运货22吨,2辆大车与6辆小车一次可以运货23吨.请根据以上信息,提出一个能用方程(组)解决的问题,并写出这个问题的解答过程.【答案】本题的答案不唯一,如:1辆大车与1辆小车一次可以运货多少吨?6.5吨.考点:1.二元一次方程组的应用;2.开放型.16.(2015广东省)某电器商场销售A 、B 两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A 型号和1台B 型号计算器,可获利润76元;销售6台A 型号和3台B 型号计算器,可获利润120元. (1)求商场销售A 、B 两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)(2)商场准备用不多于2500元的资金购进A 、B 两种型号计算器共70台,问最少需要购进A 型号的计算器多少台?【答案】(1)A 种型号计算器的销售价格是42元,B 种型号计算器的销售价格是56元;(2)30. 【解析】试题分析:(1)首先设A 种型号计算器的销售价格是x 元,B 种型号计算器的销售价格是y 元,根据题意列出方程组,再解即可;(2)根据题意表示出所用成本,进而得出不等式求出即可.试题解析:(1)设A 种型号计算器的销售价格是x 元,B 种型号计算器的销售价格是y 元,由题意得:⎩⎨⎧=-+-=-+-120)40(3)30(67640)30(5y x y x ,解得:⎩⎨⎧==5642y x ;答:A 种型号计算器的销售价格是42元,B 种型号计算器的销售价格是56元; (2)设购进A 型计算器a 台,则购进B 台计算器:(70﹣a )台,则30a+40(70﹣a )≤2500,解得:a≥30,答:最少需要购进A 型号的计算器30台.考点:1.一元一次不等式的应用;2.二元一次方程组的应用;3.综合题. 17.(2015三明)某一天,蔬菜经营户老李用了145元从蔬菜批发市场批发一些黄瓜和茄子,到菜市场去卖,黄瓜和茄子当天的批发价与零售价如下表所示:当天他卖完这些黄瓜和茄子共赚了90元,这天他批发的黄瓜和茄子分别是多少千克?【答案】黄瓜15千克,茄子25千克. 【解析】试题分析:设批发的黄瓜是x 千克,茄子是y 千克,根据题意列出方程组解答即可.试题解析:设批发的黄瓜是x 千克,茄子是y 千克,由题意得:34145(43)(74)90x y x y +=⎧⎨-+-=⎩,解得:1525x y =⎧⎨=⎩. 答:这天他批发的黄瓜15千克,茄子是25千克. 考点:二元一次方程组的应用.18.(2015吉林省)根据图中的信息,求梅花鹿和长颈鹿现在的高度.【答案】梅花鹿的高度是1.5m ,长颈鹿的高度是5.5m .考点:二元一次方程组的应用.19.(2015张家界)小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?【答案】平路为300m,下坡路为400m.【解析】试题分析:设平路有xm,下坡路有ym,根据相等关系“从家里到学校走平路和下坡路一共用10分钟,从学校到家里走上坡路和平路一共用15分钟”,列出方程组解答即可.试题解析:设平路有xm,下坡路有ym,根据题意得:106080156040x yx y⎧+=⎪⎪⎨⎪+=⎪⎩,解得:300400xy=⎧⎨=⎩.答:小华家到学校的平路为300m,下坡路为400m.考点:二元一次方程组的应用.20.(2015呼和浩特)若关于x、y的二元一次方程组23224x y mx y+=-+⎧⎨+=⎩的解满足32x y +>-,求出满足条件的m 的所有正整数值.【答案】1,2,3.考点:1.二元一次方程组的解;2.一元一次不等式的整数解.21.(2015日照)已知关于x ,y 的二元一次方程组23352x y x y m +=⎧⎨+=+⎩的解满足0x y +=,求实数m 的值.【答案】4. 【解析】试题分析:先把m 当作已知条件求出x 、y 的值,再根据足0x y +=求出m 的值即可.试题解析:解关于x ,y 的二元一次方程组23352x y x y m +=⎧⎨+=+⎩得:2117x m y m =-⎧⎨=-⎩,∵0x y +=,∴2m ﹣11+7﹣m=0,解得m=4.考点:二元一次方程组的解.22.(2015巴彦淖尔)我市某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱? 【答案】160元.考点:1.二元一次方程组的应用;2.二元一次方程的应用.23.(2015株洲)P表示n边形对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么P与n的关系式是2(1)•()24n nP n an b-=-+(其中a,b是常数,n≥4).(1)填空:通过画图可得:四边形时,P= (填数字);五边形时,P= (填数字)(2)请由四边形和五边形对角线的交点个数,结合关系式,求a和b的值.(注:本题中的多边形均指凸多边形)【答案】(1)1,5;(2)a=5,b=6.【解析】试题分析:(1)由题意画出图形,进而得出四边形和五边形中P的值;(2)利用(1)中所求,得出二元一次方程组进而求出即可.考点:1.二元一次方程组的应用;2.多边形的对角线. 24.(2015滨州)根据要求,解答下列问题: (1)解下列方程组(直接写出方程组的解即可)①2323x y x y +=⎧⎨+=⎩的解为 ,②32102310x y x y +=⎧⎨+=⎩的解为 ,③2424x y x y -=⎧⎨-+=⎩的解为 ;(2)以上每个方程组的解中,x 值与y 值的大小关系为 ; (3)请你构造一个具有以上外形特征的方程组,并直接写出它的解.【答案】(1)①11x y =⎧⎨=⎩,②22x y =⎧⎨=⎩,③44x y =⎧⎨=⎩;(2)x y =;(3)答案不唯一,如:32252325x y x y +=⎧⎨+=⎩,解为55x y =⎧⎨=⎩. 【解析】试题分析:(1)观察方程组发现第一个方程的x 系数与第二个方程y 系数相等,y 系数与第二个方程x 系数相等,分别求出解即可; (2)由每个方程组的解,得到x 与y 的关系; (3)由得出的规律写出方程组,并写出解即可.试题解析:(1)①解为11x y =⎧⎨=⎩;②解为22x y =⎧⎨=⎩;③解为44x y =⎧⎨=⎩; (2)以上每个方程组的解中,x 值与y 值的大小关系为x y =;(3)32252325x y x y +=⎧⎨+=⎩,解为55x y =⎧⎨=⎩. 考点:二元一次方程组的解.25.(2015朝阳)为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,如表中是某省的电价标准(每月).例如:方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元;李先生家5月份用电460度,交费316元,请问表中二档电价、三档电价各是多少?【答案】二档电价是0.7元/度、三档电价是0.9元/度.考点:二元一次方程组的应用.26.(2015鄂尔多斯)某足球协会举办了一次足球联赛,其记分规定及奖励方案如下表:当比赛进行到第11轮结束(每队均须比赛11场)时,A队共积17分,每赛一场,每名参赛队员均得出场费300元.设A队其中一名参赛队员所得的奖金与出场费的和为w(元).(1)试说明w是否能等于11400元.(2)通过计算,判断A队胜、平、负各几场,并说明w可能的最大值.【答案】(1)不能;(2)A队胜3场,平8场,负0场或胜4场,平5场,负2场或胜5场,平2场,负4场,11200.考点:1.一次函数的应用;2.二元一次方程的应用;3.二元一次方程组的应用;4.最值问题;5.分类讨论;6.综合题;7.压轴题.27.(2015桂林)“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).(1)求每本文学名著和动漫书各多少元?(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.【答案】(1)文学名著40元,动漫书18元;(2)有三种方案,具体见试题解析.【解析】试题分析:(1)设每本文学名著x元,动漫书y元,根据题意列出方程组解答即可;(2)根据学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,列出不等式组,解答即可.试题解析:(1)设每本文学名著x元,动漫书y元,根据题意得:20401520 2020440 x yx y+=⎧⎨-=⎩,解得:4018xy=⎧⎨=⎩.考点:1.一元一次不等式组的应用;2.二元一次方程组的应用;3.方案型;4.综合题.28.(2015义乌)某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD 上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮.(1)如图1,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比AM:AN=8:9,问通道的宽是多少?(2)为了建造花坛,要修改(1)中的方案,如图2,将三条通道改为两条通道,纵向的宽度改为横向宽度的2倍,其余四块草坪相同,且每一块草坪均有一边长为8m,这样能在这些草坪建造花坛.如图3,在草坪RPCQ中,已知RE⊥PQ于点E,CF⊥PQ于点F,求花坛RECF的面积.【答案】(1)1m;(2)13.44m2.【解析】试题分析:(1)利用AM:AN=8:9,设通道的宽为xm,AM=8ym,则AN=9y,进而利用AD为18m,宽AB为13m得出等式求出即可;(2)根据题意得出纵向通道的宽为2m,横向通道的宽为1m,进而得出PQ,RE 的长,即可得出PE、EF的长,进而求出花坛RECF的面积.试题解析:(1)设通道的宽为xm,AM=8ym,∵AM:AN=8:9,∴AN=9y,∴24181813x yx y+=⎧⎨+=⎩,解得:123xy=⎧⎪⎨=⎪⎩.考点:1.二元一次方程组的应用;2.勾股定理的应用.29.(2015珠海)阅读材料:善于思考的小军在解方程组2534115x yx y+=⎧⎨+=⎩①②时,采用了一种“整体代换”的解法:将方程②变形:4x+10y+y=5 即2(2x+5y)+y=5③把方程①带入③得:2×3+y=5,∴y=﹣1把y=﹣1代入①得x=4,∴方程组的解为41xy=⎧⎨=-⎩.请你解决以下问题:(1)模仿小军的“整体代换”法解方程组325 9419x yx y-=⎧⎨-=⎩①②;(2)已知x,y满足方程组2222321247 2836x xy yx xy y⎧-+=⎪⎨++=⎪⎩①②.(i)求224x y+的值;(ii)求112x y+的值.【答案】(1)32x y =⎧⎨=⎩;(2)(i )17;(ii )54±. 【解析】试题分析:(1)模仿小军的“整体代换”法,求出方程组的解即可; (2)方程组整理后,模仿小军的“整体代换”法,求出所求式子的值即可. 试题解析:(1)把方程②变形:3(3x ﹣2y )+2y=19③,把①代入③得:15+2y=19,即y=2,把y=2代入①得:x=3,则方程组的解为32x y =⎧⎨=⎩;(2)(i )由①得:223(4)472x y xy +=+,即224x y +=4723xy +③,把③代入②得:2×4723xy+=36﹣xy ,解得:xy=2,则224x y +=17;(ii )∵224x y +=17,∴222(2)44x y x y xy +=++=17+8=25,∴x+2y=5或x+2y=﹣5,则112x y +=22x y xy +=54±.考点:1.解二元一次方程组;2.阅读型;3.整体思想;4.综合题.【2014年题组】1.(2014年福建莆田4分)若x 、y 满足方程组x 3y 73x y 5+=⎧⎨+=⎩,则x ﹣y 的值等于( )A. 1-B. 1C. 2D. 3 【答案】A .考点:解二元一次方程组.2.(2014年广西崇左3分)方程组x y 60x 2y 30+=⎧⎨-=⎩的解是( )A .x 70y 10=⎧⎨=-⎩B .x 90y 30=⎧⎨=-⎩C .x 50y 10=⎧⎨=⎩D .x 30y 30=⎧⎨=⎩【答案】C . 【解析】试题分析:x y 60x 2y 30+=⎧⎨-=⎩①②,①﹣②得:3y=30,即y=10,将y=10代入①得:x+10=60,即x=50,则方程组的解为x 50y 10=⎧⎨=⎩.故选C .考点:解二元一次方程组.3.(2014年湖北襄阳3分)若方程mx ny 6+=的两个解是x 1x 2,y 1y 2==⎧⎧⎨⎨==-⎩⎩ ,则m ,n 的值为( )A . 4,2B .2,4C .﹣4,﹣2D .﹣2,﹣4 【答案】A . 【解析】试题分析:将x 1x 2,y 1y 2==⎧⎧⎨⎨==-⎩⎩ 分别代入mx ny 6+=中,得:m n 62m n 6+=⎧⎨-=⎩①②,①+②得:3m=12,即m=4,将m=4代入①得:n=2. 故选A .考点:二元一次方程的解和解二元一次方程组.4.(2014年山东滨州3分)王芳同学到文具店购买中性笔和笔记本.中性笔每支0.8元,笔记本每本1.2元,王芳带了10元钱,则可供她选择的购买方案的个数为( )(两样都买,余下的钱少于0.8元) A .6 B .7 C .8 D . 9 【答案】B .考点:二元一次方程的应用.5(2014年山东泰安3分)方程5x+2y=﹣9与下列方程构成的方程组的解为x 21y 2=-⎧⎪⎨=⎪⎩的是( )A. x+2y=1B. 3x+2y=﹣8C. 5x+4y=﹣3D. 3x ﹣4y=﹣8【答案】D . 【解析】试题分析:将x 与y 的值代入各项检验即可得到结果:∵满足x 21y 2=-⎧⎪⎨=⎪⎩的方程是3x ﹣4y=﹣8,∴方程5x+2y=﹣9与方程3x ﹣4y=﹣8构成的方程组的解为x 21y 2=-⎧⎪⎨=⎪⎩.故选D . 考点:方程解的定义.6.(2014年四川宜宾3分)如图,过A 点的一次函数的图象与正比例函数y=2x 的图象相交于点B ,则这个一次函数的解析式是( )A .y=2x+3B .y=x ﹣3C .y=2x ﹣3D .y=﹣x+3【答案】D .考点:函数图象和二元一次方程组.7.(2014年黑龙江大庆3分)二元一次方程组7x 4y 135x 6y 3-=⎧⎨-=⎩的解为 .【答案】x 3y 2=⎧⎨=⎩. 【解析】试题分析:利用加减消元法求出解即可:7x 4y 135x 6y 3-=⎧⎨-=⎩①②,①×3﹣②×2得:11x=33,即x=3,将x=3代入②得:y=2,∴方程组的解为x 3y 2=⎧⎨=⎩.考点:解二元一次方程组.8.(2014年福建厦门6分)解方程组2x y 42y 15x +=⎧⎨+=⎩①②.【答案】x 1y 2=⎧⎨=⎩.【解析】试题分析:①×2﹣②得:4x ﹣1=8﹣5x ,.解得:x=1,将x=1代入①得:y=2,∴方程组的解为x 1y 2=⎧⎨=⎩.考点:解二元一次方程组.9.( 2014年广西河池8分)乔丹体育用品商店开展“超级星期六”促销活动:运动服8折出售,运动鞋每双减20元.活动期间,标价为480元的某款运动服装(含一套运动服和一双运动鞋)价格为400元.问该款运动服和运动鞋的标价各是多少元?【答案】运动服的标价分别为300元/套,运动鞋的标价分别为180元/双.考点:二元一次方程组的应用.10.(2014年贵州铜仁12分)某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:(1)这批游客的人数是多少?原计划租用多少辆45座客车?(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?【答案】租用4辆60座客车更合算【解析】试题分析:(1)方程的应用解题关键是设出未知数,找出关键描述语,确定等量关系,列出方程求解. 本题设这批游客的人数是x人,原计划租用45座客车y 辆. 关键描述语为:租用45座客车若干辆,有15人没有座位;租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满. 等量关系为:45×45座客车辆数+15=游客总数,60×(45座客车辆数﹣1)=游客总数.(2)分别计算45座客车和60座客车各自的租金,比较后再取舍.考点:二元一次方程组的应用.☞考点归纳归纳 1:二元一次方程的有关概念基础知识归纳:1、二元一次方程含有两个未知数,并且未知项的最高次数是1的整式方程叫做二元一次方程.2、二元一次方程的解使二元一次方程左右两边的值相等的一对未知数的值,叫做二元一次方程的一个解.3、二元一次方程组两个(或两个以上)二元一次方程合在一起,就组成了一个二元一次方程组.4二元一次方程组的解使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值,叫做二元一次方程组的解.基本方法归纳:判断一个方程是不是二元一次方程关键看未知数的个数和未知项的最高次数;判断方程组的解只需带入方程组组看是不是成立即可.注意问题归纳:判断一个方程是不是二元一次方程特别注意是:未知项的最高次数而不是未知数的次数.【例1】方程组x y12x y5+=⎧⎨-=⎩的解是()A.x1y2=-⎧⎨=⎩ B.x2y3=-⎧⎨=⎩ C.x2y1=⎧⎨=⎩ D.x2y1=⎧⎨=-⎩【答案】D.考点:方程组的解.归纳 2:二元一次方程的解法基础知识归纳:解一元二次方程组的方法(1)代入法(2)加减法基本方法归纳:解一元二次方程组的方法关键是消元。