多元统计分析作业一

1．多元分析研究的是多个随机变量及其相互关系的统计总体。

2．多元统计中常用的统计量有：样本均值、样本方差、样本协方差和样本相关系数。

3．协方差和相关系数仅仅是变量间离散程度的一种度量，并不能刻画变量间可能存在的关联程度。

4．人们通过各种实践，发现变量之间的相互关系可以分成相关和不相关两种类型。

5．总离差平方和可以分解为回归离差平方和和剩余离差平方和两个部分，各自的自由度为p 和n-p-1，其中回归离差平方和在总离差平方和中所占比重越大，则线性回归效果越显著。

7．偏相关系数是指多元回归分析中，当其他变量固定后，给定的两个变量之间的的相关系数。

8．Spss中回归方程的建模方法有一元线形回归、多元线形回归、岭回归、多对多线形回归等。

9．主成分分析是通过适当的变量替换，使新变量成为原变量的综合变量，并寻求相关性的一种方法。

10．主成分分析的基本思想是：设法将原来众多具有一定相关性（比如P个指标），重新组合成一组新的互相无关的综合指标来代替原来的指标。

11．主成分的协方差矩阵为对角矩阵。

12．主成分表达式的系数向量是相关系数矩阵的特征向量。

13．原始变量协方差矩阵的特征根的统计含义是原始数据的相关系数。

14．原始数据经过标准化处理，转化为均值为0 ，方差为1 的标准值，且其协方差矩阵与相关系数矩阵相等。

15．样本主成分的总方差等于1 。

16．变量按相关程度为，在相关性很强程度下，主成分分析的效果较好。

17．在经济指标综合评价中，应用主成分分析法，则评价函数中的权数为方差贡献度。

19．因子分析是把每个原始变量分解为两部分因素，一部分是公共因子，另一部分为特殊因子。

20．变量共同度是指因子载荷矩阵中第i行元素的平方和。

21．公共因子方差与特殊因子方差之和为 1 。

22．聚类分析是建立一种分类方法，它将一批样哂或变量按照它们在性质上的亲疏程度进行科学的分类。

23．Q型聚类法是按样品进行聚类，R型聚类法是按变量进行聚类。

多元统计分析实验报告实验课程名称多元统计分析实验项目名称多元统计理论的计算机实现年级 2013专业应用统计学学生姓名侯杰成绩理学院实验时间：2015 年05 月07 日学生所在学院：理学院专业：应用统计学班级：9131137001代码及运行结果分析1、均值检验问题重述：某医生观察了16名正常人的24小时动态心电图，分析出早晨3小时各小时的低频心电频谱值（LF）、高频心电频谱值（HF），数据见压缩包，试分析这两个指标的各次重复测定均值向量是否有显著差异。

代码如下：Tsq.test<-function(data,alpha=0.05){data<-as.matrix(read.table("ch37.csv",header=TRUE,sep=",")) #读取数据xdat<-data[,2:4];xbar<-apply(xdat,2,mean); #计算LF指标的均值ydat<-data[,5:7];ybar<-apply(ydat,2,mean); #计算HF指标数据xcov<-cov(xdat); #计算LF样本协差阵ycov<-cov(ydat); #计算HF样本协差阵sinv<-solve(xcov+ycov);#求逆矩阵Tsq<-(16+16-2)*t(sqrt(16*16/(16+16)*(xbar-ybar)))%*%sinv%*%sqrt(16*16/(16+16)*(xbar-ybar)); #计算T统计量Fstat<-((16+16-2)-3+1)/((16+16-2)*3)*Tsq; #计算F统计量pvalue<-as.numeric(1-pf(Fstat,3,16+16-3-1));cat("p值=",pvalue,"\n");if(pvalue>0.05) #结果输出cat('均值向量不存在差异')elsecat('均值向量存在差异');}运行结果及分析：通过运行程序，我们可以得到如下结果：> Tsq.test()p值= 1.632028e-14均值向量存在差异即LF与HF这两个指标的各次重复测定均值向量存在显著差异。

《多元统计分析》习题分为三部分：思考题、验证题和论文题思考题第一章绪论1﹑什么是多元统计分析？2﹑多元统计分析能解决哪些类型的实际问题？第二章聚类分析1﹑简述系统聚类法的基本思路。

2﹑写出样品间相关系数公式。

3﹑常用的距离及相似系数有哪些？它们各有什么特点？4﹑利用谱系图分类应注意哪些问题？5﹑在SAS和SPSS中如何实现系统聚类分析？第三章判别分析1﹑简述距离判别法的基本思路，图示其几何意义。

2﹑判别分析与聚类分析有何异同？3﹑简述贝叶斯判别的基本思路。

4﹑简述费歇判别的基本思路。

5﹑简述逐步判别法的基本思想。

6﹑在SAS和SPSS软件中如何实现判别分析？第四章主成分分析1﹑主成分分析的几何意义是什么？2﹑主成分分析的主要作用有那些？3﹑什么是贡献率和累计贡献率，其意义何在？4﹑为什么说贡献率和累计贡献率能反映主成分中所包含的原始变量的信息？5﹑为什么要用标准化数据去估计V的特征向量与特征值？6﹑证明：对于标准化数据有S=R。

7﹑主成分分析在SAS和SPSS中如何实现？第五章因子分析1﹑因子得分模型与主成分分析模型有何不同？2﹑因子载荷阵的统计意义是什么？3﹑方差旋转的目的是什么？4﹑因子分析有何作用？5﹑因子模型与回归模型有何不同？6﹑在SAS和SPSS中如何实现因子分析？第六章对应分析1﹑简述对应分析的基本思想。

2﹑简述对应分析的基本原理。

3﹑简述因子分析中Q型与R 型的对应关系。

4﹑对应分析如何在SAS和SPSS中实现？第七章典型相关分析1﹑典型相关分析适合分析何种类型的数据？2﹑简述典型相关分析的基本思想。

3﹑典型变量有哪些性质？4﹑典型相关系数和典型变量有何意义？5﹑典型相关分析有何作用？6 ﹑在SAS和SPSS中如何实现典型相关分析？验证题第二章聚类分析1、为了更深入了解我国人口的文化程度，现利用1990年全国人口普查数据对全国30个省、直辖市、自治区进行聚类分析。

分析选用了三个指标：(1)大学以上文化程度的人口占全部人口的比例(DXBZ)；(2)初中文化程度的人都占全部人口的比例(CZBZ)；(3)文盲半文盲人口占全部人口的比例(WMBZ)，分别用来反映较高、中等、较低文化程度人口的状况。

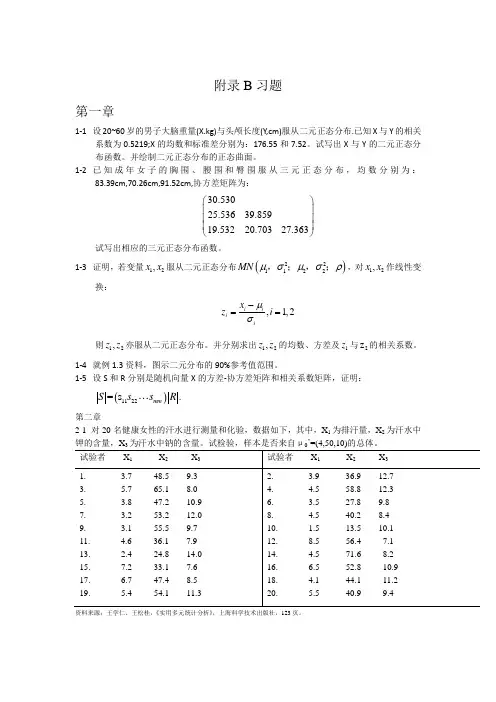
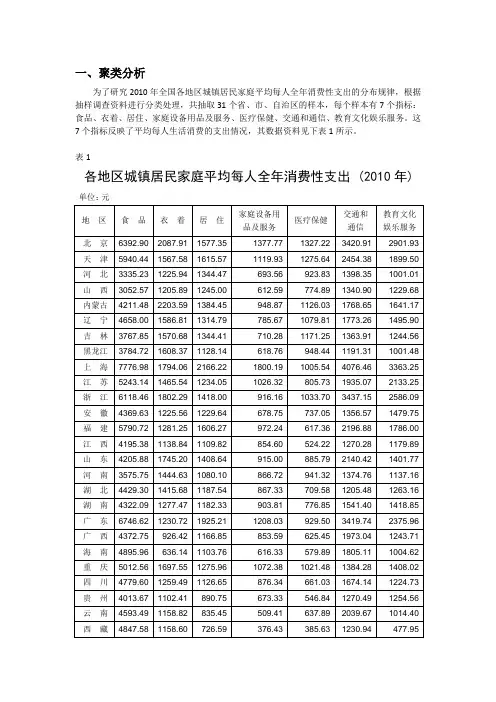
一、聚类分析为了研究2010年全国各地区城镇居民家庭平均每人全年消费性支出的分布规律，根据抽样调查资料进行分类处理，共抽取31个省、市、自治区的样本，每个样本有7个指标：食品、衣着、居住、家庭设备用品及服务、医疗保健、交通和通信、教育文化娱乐服务。

这7个指标反映了平均每人生活消费的支出情况，其数据资料见下表1所示。

表1定义变量及标签：设：X1：地区X2：食品支出X3：衣着支出X4：居住支出X5：家庭设备用品及服务支出X6：医疗保健支出X7：交通和通信支出X8：教育文化娱乐服务支出通过SPSS软件操作，得到如下输出结果见表2—表5所示。

表2表3表4表4给出了聚类的凝聚过程情况。

表5给出了样品聚为三类时的样品归类情况。

C A S E 0 5 10 15 20 25 Label Num +---------+---------+---------+---------+---------+甘肃 28 -+青海 29 -+新疆 31 -+河北 3 -+---+山西 4 -+ |河南 16 -+ |宁夏 30 -+ |黑龙江 8 -+ +-------+陕西 27 -+ | |云南 25 -+-+ | |西藏 26 -+ | | |广西 20 -+ +-+ |海南 21 -+ | |江西 14 -+-+ |贵州 24 -+ +-----------------------------------+ 湖北 17 -+ | | 湖南 18 -+ | | 四川 23 -+ | | 安徽 12 -+ | | 江苏 10 -+-+ | | 福建 13 -+ | | | 辽宁 6 -+ +---------+ | 吉林 7 -+ | | 山东 15 -+-+ | 重庆 22 -+ | 内蒙古 5 -+ | 天津 2 -+ | 浙江 11 -+-+ | 北京 1 -+ +-+ | 广东 19 ---+ +-------------------------------------------+ 上海 9 -----+图1图1是聚类全过程的树形图。

多元统计分析作业海洋地球化学多元统计分析作业一、预备工作：数据的输出管理首先设置File output manager output manager中，选中individual wind。

Also send to Report wind中，选中single report。

二、数据的导入数据表（data.xls）为一个深海沉积物柱中30个样品分析结果。

第1列为样品编号，第2列为样品的采样深度（单位），第三列起为分析的各元素含量。

将data.xls 数据导入Statistica worksheet中 (操作步骤为菜单Fileopen …data.xls)三、数据（图表）的输出统计分析过程中生成的结果都可以输出到Word文档中（菜单as …或PrtSc，粘贴到word中）。

对生成的图表，还可先菜单File Add to report，再粘贴到word中。

本项上机实习需完成以下统计分析一、相关及回归分析(Correlation matrices)1、分析两组分Co-Ni， CaO-Sr，Fe2O3-MnO，的相关关系，做出相关关系图，拟合出回归方程。

图1 Co-Ni 相关关系图图2 CaO-Sr 相关关系图图3 Fe2O3-MnO 相关关系图2、做出三组分Cu-Pb-Zn；Sr-Cu-CaO之间的散点图 (scatterplot) 。

图4 Cu-Co-Ni 散点图图5 Sr-Cu-CaO 散点图3、计算CaO、Co、Cu、Fe2O3、MnO、Ni、Sr之间的相关关系矩阵。

表1 沉积物中元素相关关系矩阵 (n=30,p<0.05)CaO Fe2O3MnO Co Cu Ni SrCaO 1.00Fe2O3-0.23 1.00MnO 0.18 0.18 1.00Co -0.21 0.85 0.41 1.00Cu -0.02 -0.01 0.36 0.26 1.00Ni -0.10 0.96 0.24 0.88 -0.03 1.00Sr 0.97 -0.25 0.23 -0.20 0.09 -0.13 1.00二、聚类分析(Cluster analysis)1、首先将数据进行标准化(分别进行和列的标准化)，得到标准化的数据集。

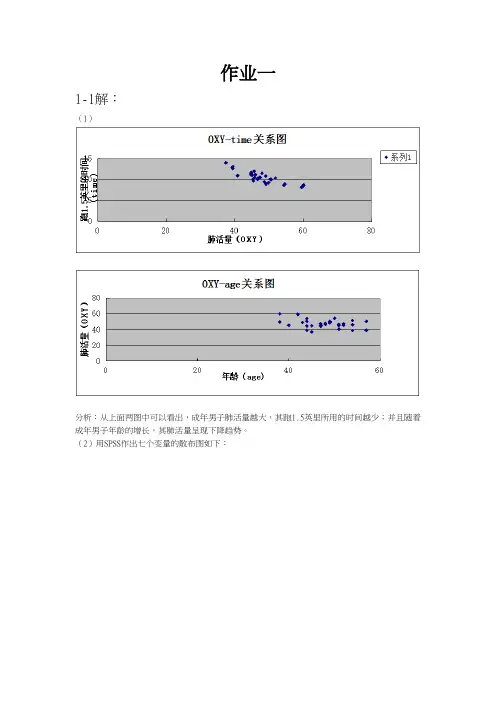
作业一1-1解：（1）分析：从上面两图中可以看出，成年男子肺活量越大，其跑1.5英里所用的时间越少；并且随着成年男子年龄的增长，其肺活量呈现下降趋势。

（2）用SPSS作出七个变量的散布图如下：（3）绘制序号为1,2,21,22的四个人的雷达图：其中系列1，2,3,4分别表示绘制序号为1,2,21,22的四个人的数据绘制序号为1,2,21,22的四个人的轮廓图： 程序代码：X=[57 73.37 12.63 58 174 176 39.407; 54 79.38 11.17 62 156 165 46.08; 49 73.37 10.08 76 168 168 50.388; 44 89.47 11.37 62 178 182 44.609]t={'age','weight','time','spulse','rpulse','mpulse','OXY'}line([1:7],X')set(gca,'XTicklabel',t)ageweighttimespulserpulsempulseOX Y020406080100120140160180200其中各颜色轮廓线表示意义同上（3）绘制序号为1,2,21,22的四个人的调和曲线图：程序代码：t=-pi:pi/20:pi;y1=57/sqrt(2)+73.37*sin(t)+12.63*cos(t)+58*sin(2*t) +174*cos(2*t)+176*sin(3*t)+39.407*cos(3*t);y2=54/sqrt(2)+79.38*sin(t)+11.17*cos(t)+62*sin(2*t) +156*cos(2*t)+165*sin(3*t)+46.08*cos(3*t);y3=49/sqrt(2)+73.37*sin(t)+10.08*cos(t)+76*sin(2*t) +168*cos(2*t)+168*sin(3*t)+50.388*cos(3*t);y4=44/sqrt(2)+89.47*sin(t)+11.37*cos(t)+62*sin(2*t) +178*cos(2*t)+182*sin(3*t)+44.609*cos(3*t);plot(t,y1,t,y2,t,y3,t,y4,'linewidth',3)xlabel('t'),ylabel('f(t)')legend('f1(t)','f2(t)','f21(t)','f22(t)')-4-3-2-101234-300-200-1000100200300400500tf (t )f1(t)f2(t)f21(t)f22(t)其中f1(t),f2(t),f21(t),f22(t)分别表示绘制序号为1,2,21,22的四个人数据所对应的调和曲线。

一、填空题：1、多元统计分析是运用数理统计方法来研究解决多指标问题的理论和方法.2、回归参数显著性检验是检验解释变量对被解释变量的影响是否著.3、聚类分析就是分析如何对样品（或变量）进行量化分类的问题。

通常聚类分析分为 Q型聚类和 R型聚类。

4、相应分析的主要目的是寻求列联表行因素A 和列因素B 的基本分析特征和它们的最优联立表示。

5、因子分析把每个原始变量分解为两部分因素：一部分为公共因子，另一部分为特殊因子。

6、若()(,), Px N αμα∑=1,2,3….n且相互独立，则样本均值向量x服从的分布为_x~N(μ，Σ/n)_。

二、简答1、简述典型变量与典型相关系数的概念，并说明典型相关分析的基本思想。

在每组变量中找出变量的线性组合，使得两组的线性组合之间具有最大的相关系数。

选取和最初挑选的这对线性组合不相关的线性组合，使其配对，并选取相关系数最大的一对，如此下去直到两组之间的相关性被提取完毕为止。

被选出的线性组合配对称为典型变量，它们的相关系数称为典型相关系数。

2、简述相应分析的基本思想。

相应分析，是指对两个定性变量的多种水平进行分析。

设有两组因素A和B，其中因素A包含r个水平，因素B包含c个水平。

对这两组因素作随机抽样调查，得到一个rc的二维列联表，记为。

要寻求列联表列因素A和行因素B的基本分析特征和最优列联表示。

相应分析即是通过列联表的转换，使得因素 A 和因素B具有对等性，从而用相同的因子轴同时描述两个因素各个水平的情况。

把两个因素的各个水平的状况同时反映到具有相同坐标轴的因子平面上，从而得到因素A、B的联系。

3、简述费希尔判别法的基本思想。

从k个总体中抽取具有p个指标的样品观测数据，借助方差分析的思想构造一个线性判别函数系数：确定的原则是使得总体之间区别最大，而使每个总体内部的离差最小。

将新样品的p 个指标值代入线性判别函数式中求出 值，然后根据判别一定的规则，就可以判别新的样品属于哪个总体。

应用多元统计分析作业（一）——主成分分析 8‐1：用主成分分析方法探讨城市工业主体结构。

解：执行SAS程序代码：data dxiti81;input number x1-x8;cards;1 90342 52455 101091 19272 82 16.1 197435 0.1722 4903 1973 2035 10313 34.2 7.1 592077 0.0033 6735 21139 3767 1780 36.1 8.2 726396 0.0034 49454 36241 81557 22504 98.1 25.9 348226 0.9855 139190 203505 215898 10609 93.2 12.6 139572 0.6286 12215 16219 10351 6382 62.5 8.7 145818 0.0667 2372 6572 8103 12329 184.4 22.2 20921 0.1528 11062 23078 54935 23804 370.4 41 65486 0.2639 17111 23907 52108 21796 221.5 21.5 63806 0.27610 1206 3930 6126 15586 330.4 29.5 1840 0.43711 2150 5704 6200 10870 184.2 12 8913 0.27412 5251 6155 10383 16875 146.4 27.5 78796 0.15113 14341 13203 19396 14691 94.6 17.8 6354 1.574;proc princomp data=dxiti81 out=oxiti81;var x1-x8;run;proc sort data=oxiti81;by prin1;proc print;id number;var prin1;run;proc sort data=oxiti81;by prin2;proc print;id number;var prin2;run;proc sort data=oxiti81;by prin3;proc print;id number;var prin3;run;proc plot;plot prin2*prin1=number;run;proc cluster data=oxiti81 method=ave pseudo ccc outtree=tr81;var x1-x8;id number;proc tree data=tr81 horizontal graphics;run;结果分析：◆我们使用原始数据的相关系数矩阵计算特征根矩阵。

应用多元统计分析作业多元统计分析是一种广泛应用于科学研究和商业决策中的数据分析方法。

它通过同时考虑多个变量之间的关系和差异，能够更全面地了解数据的特征和规律。

本文将介绍多元统计分析的应用及其在作业中的实际运用。

首先，多元统计分析在科学研究中具有广泛的应用。

研究人员可以通过多元统计方法来探索不同变量之间的关系，发现隐藏在数据背后的规律。

例如，在医学领域中，研究人员可以使用多元统计分析来研究疾病的发病机制和影响因素。

他们可以收集患者的各种指标数据，并通过多元统计分析方法来确定哪些变量与疾病的发展和治疗效果相关。

这有助于为疾病的早期诊断和治疗提供科学依据。

其次，多元统计分析在商业决策中也有重要的应用。

企业可以使用多元统计方法来了解市场需求、消费者行为和产品特点等因素之间的关系。

通过收集大量的市场调查数据，企业可以使用多元统计分析来找出不同群体之间的差异和共同点。

这有助于企业更好地了解消费者的需求，优化产品设计和市场推广策略，提高企业竞争力。

在学术研究和商业决策中，多元统计分析方法的应用是非常复杂的，需要使用专门的统计软件进行计算和分析。

例如，研究人员可以使用SPSS、SAS等统计软件来进行多元方差分析、主成分分析、聚类分析等多元统计分析方法。

这些软件提供了丰富的统计工具和图表，可以通过可视化方式展示数据分析结果，便于研究人员和决策者进行数据分析和决策。

在作业中，多元统计分析也是一个重要的课题。

学生可以使用多元统计分析方法来解决实际问题，提高数据处理和分析的能力。

例如，学生可以选择一个感兴趣的研究主题，收集相关数据，并使用多元统计分析方法来探索不同变量之间的关系。

这有助于学生深入了解数据分析方法的原理和应用，提高解决实际问题的能力。

总之，多元统计分析是一种有效的数据分析方法，广泛应用于科学研究和商业决策中。

它能够帮助人们更全面地了解数据的特征和规律，并提供科学依据来支持决策。

在作业中，多元统计分析也是一个重要的课题，可以帮助学生提高数据处理和分析的能力。