应用多元统计分析SAS作业第六章资料

应用多元统计分析S A S作业YKK standardization office【 YKK5AB- YKK08- YKK2C- YKK18】5-9 设在某地区抽取了14块岩石标本，其中7块含矿，7块不含矿。

对每块岩石测定了Cu，Ag，Bi三种化学成分的含量，得到的数据如表1。

表1 岩石化学成分的含量数据(1)假定两类样本服从正态分布，使用广义平方距离判别法进行判别归类（先验概率取为相等，并假定两类样本的协方差阵相等）；(2)今得一块标本，并测得其Cu，Ag，Bi的含量分别为2.95，2.15和1.54，试判断该标本是含矿还是不含矿？问题求解1 使用广义平方距离判别法对样本进行判别归类用SAS软件中的DISCRIM过程进行判别归类。

SAS程序及结果如下。

data d59;input group x1-x3@@;cards;1 2.58 0.9 0.951 2.9 1.23 11 3.55 1.15 11 2.35 1.15 0.791 3.54 1.85 0.791 2.7 2.23 1.31 2.7 1.7 0.482 2.25 1.98 1.062 2.16 1.8 1.062 2.33 1.74 1.12 1.96 1.48 1.042 1.94 1.4 1 23 1.3 1 2 2.78 1.7 1.48 ；proc print data =d59; run ;proc discrim data =d59 pool =yes distance list ; class group; var x1-x3; run ;由输出结果可知，两总体间的广义平方距离为D 2=3.19774。

还可知两个三元总体均值相等的检验结果：D =3.19774，F =3.10891，p =0.0756<0.10，故在显着性水平=0.10α时量总体的均值向量有显着差异，即认为讨论这两个三元总体的判别问题是有意义的。

多元统计分析实验报告学院名称理学院专业班级应用统计学14-2学生姓名张艳雪学号201411081051工资、受教育年限、初始工资和工作经验资料如下表所示： 设职工总体的以上变量服从多元正态分布，根据样本资料利用 SPSS 软件求出均注 1：最大似然估计公式为： μˆ = X = ∑ ∑ (X i - X )(X i - X )' ； ˆ第一章 多元正态分布1.1 从某企业全部职工中随机抽取一容量为 6 的样本，该样本中个职工的目前值向量和协方差矩阵的最大似然估计。

1 n n i =1 X i ， Σ = 1 nn i =1一．SPSS 操作步骤：第一步：利用 spss 建立数据集第二步：分析--描述统计--描述 计算样本均值向量 第三步：分析--相关--双变量计算样本协方差阵与样本相关系数二．输出结果：⎪ μ= 37125 ⎪ 152.50⎪ ⎛ 352068000 12500 -110677500 102000 ⎫= -110677500 - 86250 2192793750 691125 ⎪16695.1⎪⎭ ∑ X i，∑ (X i - X )(X i - X )'ˆ三．实验结果分析：样本均值为样本的协方差∑⎪⎪如此就可以按照极大似然估计方程：1 nΣ =n i =1得出均值向量与协方差向量的最大似然估计结果。

μ=X=1nn i=1ˆ第三章聚类分析3.1下表是15个上市公司2001年的一些主要财务指标，使用系统聚类法和K－均值法利用SPSS软件分别对这些公司进行聚类，并对结果进行比较分析。

公司编号净资产收益率每股净利润总资产周转率资产负债率流动负债比率每股净资产净利润增长率总资产增长率111.090.210.0596.9870.53 1.86-44.0481.99211.960.590.7451.7890.73 4.957.0216.11300.030.03181.99100-2.98103.3321.18411.580.130.1746.0792.18 1.14 6.55-56.325-6.19-0.090.0343.382.24 1.52-1713.5-3.366100.470.4868.486 4.7-11.560.85710.490.110.3582.9899.87 1.02100.2330.32811.12-1.690.12132.14100-0.66-4454.39-62.759 3.410.040.267.8698.51 1.25-11.25-11.4310 1.160.010.5443.7100 1.03-87.18-7.411130.220.160.487.3694.880.53729.41-9.97128.190.220.3830.31100 2.73-12.31-2.771395.79-5.20.5252.3499.34-5.42-9816.52-46.821416.550.350.9372.3184.05 2.14115.95123.4115-24.18-1.160.7956.2697.8 4.81-533.89-27.74一、实验原理:1.系统聚类的基本思想是：首先，每个样品（或变量）先聚成一类，然后，选择距离公式计算类与类之间的距离，把距离相近的样品（或变量）先聚成类，距离相远的后聚成类，该过程一直进行下去，每个样品（或变量）总能聚到合适的类中，最后，所有的样品（或变量）聚成一类。

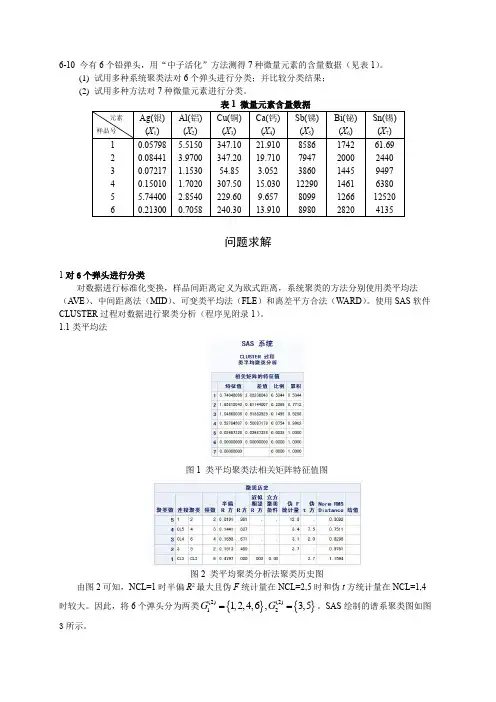
6-10 今有6个铅弹头，用“中子活化”方法测得7种微量元素的含量数据（见表1）。

(1) 试用多种系统聚类法对6个弹头进行分类；并比较分类结果； (2) 试用多种方法对7种微量元素进行分类。

问题求解1对6个弹头进行分类对数据进行标准化变换，样品间距离定义为欧式距离，系统聚类的方法分别使用类平均法（A VE ）、中间距离法（MID ）、可变类平均法（FLE ）和离差平方合法（WARD ）。

使用SAS 软件CLUSTER 过程对数据进行聚类分析（程序见附录1）。

1.1类平均法图1 类平均聚类法相关矩阵特征值图图2 类平均聚类分析法聚类历史图由图2可知，NCL=1时半偏R 2最大且伪F 统计量在NCL=2,5时和伪t 方统计量在NCL=1,4时较大。

因此，将6个弹头分为两类{}{}(2)(2)121,2,4,6,3,5G G ==。

SAS 绘制的谱系聚类图如图3所示。

图3 类平均聚类分析法谱系聚类图1.2中间距离法图4 中间距离聚类法相关矩阵特征值图图5 中间距离聚类法聚类历史图由图5可知，中间距离法与类平均法结果一致。

因此，也将6个弹头分为两类{}{}(2)(2)121,2,4,6,3,5G G ==。

SAS 绘制的谱系聚类图如图6所示。

图6中间距离聚类法谱系聚类图1.3可变类平均法图7可变类平均聚类法分析结果图图8 可变类平均聚类法聚类历史图由图8可知，可变类平均法(=0.25β-)输出结果与前两种方法稍有不同，NCL=1时半偏R2最大且伪F统计量在NCL=2时次大，NCL=5时最大；而伪t方统计量在NCL=1时最大。

因此，分类结果与之前相同，将6个弹头分为两类{}{}(2)(2)121,2,4,6,3,5G G ==。

SAS 绘制的谱系聚类图如图9所示。

图9 可变类平均聚类法谱系聚类图1.4离差平方和法图10 离差平方和聚类法相关矩阵特征值图图11 离差平方和聚类法聚类历史由图11可知，离差平方和法输出结果与可变类平均法结果一致。

《应用多元分析》（第三版）各章附录中SAS程序的说明等（王学民编）附录1-1 SAS的应用例1—1.1的SAS程序:proc iml；x={1 2 3 4 5,2 4 7 8 9，3 7 10 15 20,4 8 15 30 20,5 9 20 20 40｝；g=inv（x);e=eigval（x）；d=eigvec(x)；h=det（x）；t=trace（x)；print g e d h t；程序说明:“proc iml"是一个矩阵运算的过程步;“x={1 2 3 4 5,2 4 7 8 9,3 7 10 15 20，4 815 30 20,5 9 20 20 40}”是输入矩阵1234524789371015204815302059202040⎛⎫⎪⎪⎪⎪⎪⎪⎝⎭,并赋值给变量x；inv（x）是x的逆矩阵函数，eigval（x）是x的特征值函数，eigvec(x）是x的特征向量函数,det（x) 是x的行列式函数,trace（x)是x的迹函数，这些函数分别赋值给我们取的变量g，e，d，h，t；“print g e d h t”是打印语句，指定将g e d h t的值输出。

附录2—1 SAS的应用例2.3。

3和例2。

3.6的SAS程序:proc iml;a={2 -1 4,0 1 —1，1 3 -2｝;b=｛5，-2，7｝;c=｛4 1 2，1 9 —3，2 —3 25｝；d=block（2,3,5）;e=a*b；v=a＊c*t（a）；r=inv（d)*c*inv（d）;print e v r；程序说明：“proc iml”是一个矩阵运算的过程步；“a={2 —1 4,0 1 —1，1 3 -2｝”是输入矩阵214011132-⎛⎫⎪-⎪⎪-⎝⎭，并赋值给变量a；“b=｛5,—2，7}"是输入向量527⎛⎫⎪- ⎪⎪⎝⎭，并赋值给变量b；“c=｛4 1 2,1 9 -3,2 -3 25｝”是输入矩阵4121932325⎛⎫⎪-⎪⎪-⎝⎭，并赋值给变量c;“d=block(2,3,5）”是输入对角阵diag(2，3，5）,并赋值给变量d;“e=a*b”是将a与b相乘,并赋值给变量e；“v=a＊c*t(a)”是将a，c，a’三个矩阵相乘，并赋值给变量v,其中t(a)是a的转置函数；“r=inv（d）*c＊inv(d)”是将d-1,c,d-1相乘，并赋值给变量r，其中inv(d)是d的逆矩阵函数；”print e v r”是打印语句，指定将e v r的值输出.附录3-1 SAS的应用例3-1.1的SAS程序：proc corr data=sasuser.examp3a1 cov;var x1—x7；run；proc corr data=sasuser.examp3a1 nosimple cov;var x5 x6 x7;with x3 x4;partial x1 x2;run;程序说明：Proc步是以proc开头的一组或几组语句,它以另一个proc步、data步或run语句结束。

SAS系统 与基础统计分析计算机统计分析软件 (SAS系统9.1.3)1SAS与基础统计分析目录 1. 统计基本概念 2. 频率分布和常用描述统计量 3. 计算描述统计量的常用过程 4. 直方图和分布的拟合检验 5. 参数估计 6. 假设检验2统计基本概念SAS统计分析的功能SAS分析的特点(1) SAS 将常用的统计方法用过程实现,是一个高品位 的程序系统; (2) SAS 是一个迅速发展的系统：融入最新的方法， 不断适应用户的新需求; (3) SAS 既可由编程也可用图形界面交互地实现分析 功能; (4) SAS 将各种专门分析方法融入为用户提供的直接 使用的专用系统中--应用系统.3统计基本概念SAS统计分析的功能如何学习SAS统计分析的功能会找: 针对问题和数据选用合适的分析工具. 会用： 选PROC(过程)，选Option(选项), 写Statement(语句), 或选用菜单系统. 会解释：对SAS提供的计算结果给出解释和 分析.4统计基本概念统计的基本概念—统计的过程 总体（分布及其它特征） 抽样 样本（分布及其它特征） 推断 计算统计量 统计量 描述5统计基本概念统计的基本概念参数是总体的特征量。

统计量是由样本观测值计算而得到的。

统计量可用于估计总体的参数。

总体参数 均值 方差 标准差σμ样本统计量2σX 2 ss6统计基本概念抽样的随机性 总 子样 子样 体 子样 子样 子样对同一个总体可以获得多个不同的样本.这 些样本的观测值不全相同，相应的统计量也 不一样，这是由抽样偶然性引起的.但当样本 的容量增大时，由不同样本计算的统计量之 间的差异逐渐缩小，这是统计的规律性.7统计基本概念描述性统计和推断性统计利用样本计算得到的各种统计量(包括 图形)可以： (1)进行描述统计,即描述样本的各种主要 特征； (2)进行推断统计,即扩大所收集到的信 息的使用范围,用样本的特征来推断 总体的特征。

前言多元统计分析是统计学中内容十分丰富、应用性极强的一个重要分支，它在自然科学、社会科学和经济学等各领域中得到了越来越广泛的应用，是一种非常重要和实用的多元数据处理方法。

本书此次又在第二版的基础上作了较大幅度的改写和扩充，使之更能适应当今统计教学的需要。

本教材主要是针对财经类院校的统计学和数理统计学专业的本科生而写的，也可作为其他各专业读者的多元统计分析教材或教学参考书。

整本书写得比较细致，便于自学，书中的绝大部分内容曾向上海财经大学统计学系的本科生和研究生分别讲授过十多届。

本教材有如下一些特点：(1)全书对数学基础知识的要求较低，只需读者掌握初步的微积分、线性代数和概率统计知识。

尽管如此，为便于非统计专业的读者也能顺利地阅读本书，书中前几个章节对矩阵代数及一元统计知识作了简单的回顾和介绍，其所述的预备知识内容对于本书的阅读基本上已足够了。

(2)本教材以简明和深入浅出的方式阐述了多元统计分析的基本概念、统计思想和数据处理方法，在充分考虑到适合财经院校学生使用的前提下进行了严谨的论述，有助于学生深刻地理解并掌握多元分析的基本思想方法。

(3)书中提供的许多例题和习题为读者展示了多元分析在社会科学和经济学等领域中的应用，每章的例题和习题安排侧重于对基本概念的理解和知识的实际应用，并不注重解题的数学技巧和难度。

为便于读者的学习（特别是自学），书后的附录一给出了习题参考答案及部分解答。

(4)本书与SAS软件紧密结合，在每一章后面都附有SAS的应用，这有利于将SAS软件更好地融入各章的内容中，使读者对多元分析的意义能够有贴切的体会，便于读者进入应用的领域。

全书共分十章。

第一章介绍了多元分析中常用的矩阵代数知识，这是全书的基础。

第二章至第四章介绍的基本上是一元统计推广到多元统计的内容，主要阐述了多元分布的基本概念和多元正态分布及其统计推断。

第五章至第十章是多元统计独有的内容，这部分内容具有很强的实用性，特别是介绍了各种降维技术，将原始的多个指标化为少数几个综合指标，便于对数据进行分析。

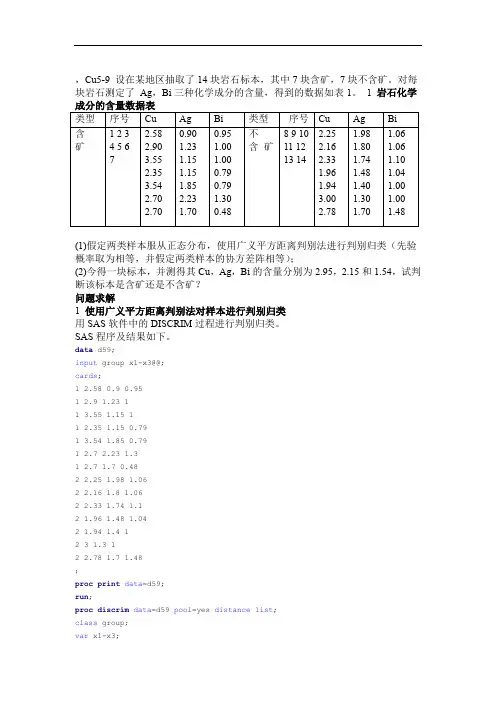
，Cu5-9 设在某地区抽取了14块岩石标本，其中7块含矿，7块不含矿。

对每块岩石测定了Ag，Bi三种化学成分的含量，得到的数据如表1。

1 岩石化学(1)假定两类样本服从正态分布，使用广义平方距离判别法进行判别归类（先验概率取为相等，并假定两类样本的协方差阵相等）；(2)今得一块标本，并测得其Cu，Ag，Bi的含量分别为2.95，2.15和1.54，试判断该标本是含矿还是不含矿？问题求解1 使用广义平方距离判别法对样本进行判别归类用SAS软件中的DISCRIM过程进行判别归类。

SAS程序及结果如下。

data d59;input group x1-x3@@;cards;1 2.58 0.9 0.951 2.9 1.23 11 3.55 1.15 11 2.35 1.15 0.791 3.54 1.85 0.791 2.7 2.23 1.31 2.7 1.7 0.482 2.25 1.98 1.062 2.16 1.8 1.062 2.33 1.74 1.12 1.96 1.48 1.042 1.94 1.4 12 3 1.3 12 2.78 1.7 1.48；proc print data=d59;run;proc discrim data=d59 pool=yes distance list;class group;var x1-x3;run2还可知两个三元总体均值相等由输出结果可知，两总体间的广义平方距离为D。

=3.19774?=0.10时量总体的均，故在显着性水平，p=0.0756<0.10的检验结果：D=3.19774，F=3.10891 值向量有显着差异，即认为讨论这两个三元总体的判别问题是有意义的。

线性判别函数为：号样本错判为含矿。

判别结果为含矿的6号样本错判为不含矿；不含矿的13对给定样本判别归类2分别代入线性判别函数得：、2.15、1.54将Cu，Ag，Bi的含量数值2.9546.97888?44.67422，YY?。

sas应用多元分析课程设计一、课程目标知识目标：1. 掌握SAS软件的基本操作和功能，理解多元分析的基本概念和原理；2. 学习并掌握常用的多元分析方法，如因子分析、聚类分析、判别分析等；3. 了解多元分析在实际问题中的应用场景，能运用所学知识解决实际问题。

技能目标：1. 能够运用SAS软件进行多元分析操作，熟练运用相关命令和函数；2. 能够根据实际问题选择合适的多元分析方法，并进行数据处理和分析；3. 能够对多元分析结果进行正确解读和评价，提出有效的数据见解。

情感态度价值观目标：1. 培养学生对数据分析的兴趣，激发主动学习和探索精神；2. 培养学生严谨的科学态度，注重数据真实性和分析客观性；3. 培养学生团队协作意识，提高沟通与交流能力。

课程性质：本课程为应用型课程，结合实际案例，强调理论与实践相结合。

学生特点：学生具备一定的统计学基础和计算机操作能力，对数据分析感兴趣。

教学要求：以学生为中心，注重培养实际操作能力和解决问题能力，鼓励学生积极参与讨论和思考。

在教学过程中，将课程目标分解为具体的学习成果，便于教学设计和评估。

二、教学内容1. SAS软件基础操作与功能介绍：包括数据导入、数据清洗、数据转换等基本操作，以及SAS编程语言的基本语法和常用函数。

教材章节：第一章 SAS软件概述与操作入门2. 多元分析基本概念与原理：讲解多元分析的基本思想、类型及其应用场景，如因子分析、聚类分析、判别分析等。

教材章节：第二章 多元分析概述3. 常用多元分析方法及SAS实现：a. 因子分析：介绍因子分析的原理、步骤及SAS实现方法。

教材章节：第三章 因子分析b. 聚类分析：讲解聚类分析的原理、方法及SAS操作。

教材章节：第四章 聚类分析c. 判别分析：阐述判别分析的原理、步骤及SAS应用。

教材章节：第五章 判别分析4. 实际案例分析与数据处理：结合实际问题，引导学生运用所学知识进行数据分析，提高解决实际问题的能力。

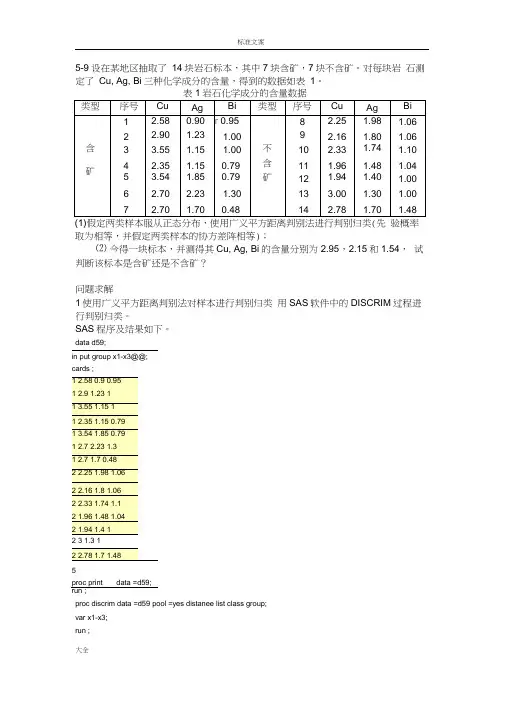
标准文案5-9设在某地区抽取了14块岩石标本，其中7块含矿，7块不含矿。

对每块岩石测定了Cu, Ag, Bi三种化学成分的含量，得到的数据如表1。

表1岩石化学成分的含量数据(1)假定两类样本服从正态分布，使用广义平方距离判别法进行判别归类(先验概率取为相等，并假定两类样本的协方差阵相等)；⑵今得一块标本，并测得其Cu, Ag, Bi的含量分别为2.95，2.15和1.54，试判断该标本是含矿还是不含矿？问题求解1使用广义平方距离判别法对样本进行判别归类用SAS软件中的DISCRIM过程进行判别归类。

SAS程序及结果如下。

data d59;in put group x1-x3@@;cards ;1 2.58 0.9 0.951 2.9 1.23 11 3.55 1.15 11 2.35 1.15 0.791 3.54 1.85 0.791 2.7 2.23 1.31 2.7 1.7 0.482 2.25 1.98 1.062 2.16 1.8 1.062 2.33 1.74 1.12 1.96 1.48 1.042 1.94 1.4 12 3 1.3 12 2.78 1.7 1.485proc print data =d59;run ;proc discrim data =d59 pool =yes distanee list class group;var x1-x3;run ;大全SAS 系统DJSCHIH 述程战卜鞭淮魅陽的枯冥城集WORK Db9便JB 门下血的垂樓结覃Aksrouo料青group1Z11 Q 飾55 C 34*152 » 1 0 了伽 0 22763 1 1 0 071 fi 0 Q26t A 1 1 o 63ir ： 0 BD7 5 1 1 0. B64I 9 013y G I 2 * 0 12B0 Q 8710 7 i1 0 9541 ■:關 82 2 U 1243 0 8TJ7 92 2 0 1057 0 9933 10 2 2 Q. 1533 0 8407 112 2 Q 0797 0 9213 12 2 20 0B5€ 0 DCH4由输出结果可知，两总体间的广义平方距离为D=3.19774。

应用多元统计分析1课程介绍多元统计分析(简称多元分析)是统计学的一个重要分支.它是应用数理统计学来研究多变量(多指标)问题的理论和方法; 它是一元统计学的推广和发展.多元统计分析是一门具有很强应用性的课程;它在自然科学和社会科学等各个领域中得到广泛的应用;它包括了很多非常有用的数据处理方法.第一章绪论第二章多元正态分布及参数的估计第三章多元正态总体参数的假设检验第四章回归分析--第五章判别分析第六章聚类分析第七章主成分分析第八章因子分析第九章对应分析方法第十章典型相关分析第十一章偏最小二乘回归分析本课程的内容多变量分析（数据结构简化）分类方法两组变量的相关分析基础理论两组变量的相依分析使用的教材普通高等教育”十一五”国家级教材北京大学数学教学系列丛书本科生数学基础课教材应用多元统计分析(北京大学出版社,高惠璇,2006.10)参考书（一）1. 实用多元统计分析(方开泰,1989,见参考文献[1])2. 多元统计分析引论(张尧庭,方开泰, 2003,见[2])3. 实用多元统计分析(王学仁,1990 ,见[6])4. 应用多元分析(王学民,1999 ,见[8])5. 实用统计方法与SAS系统(高惠璇,2001, 见[3])6. 多元统计分析(于秀林,1999 ,见[9])7. 多元统计方法(周光亚,1988 ,见[28])8. 多元分析(英. M . 肯德尔,1983 ,见[15])9. SAS系统使用手册等资料(1994-1998 ,见[17]-[21])参考书（二）(1) An Introduction to Multivariate Statistical Analysis(Anderson 1984 ,见[22]) (2) Applied Multivariate Statistical Analysis( Richard A.Johnson and Dean W.Wichern 4th ed 1998)中译本：实用多元统计分析（陆璇译2001 ,见[5]）(3) Linear Statistical Inference and Its Applications (C.R.Rao 1973)中译本：线性统计推断及其应用(C.R.劳1987 ,见[25])§1.1 引言在实际问题中，很多随机现象涉及到的变量不止一个，而经常是多个变量，而且这些变量间又存在一定的联系。

多元统计分析SAS期末大作业多元统计分析期末作业课本习题5.4 根据经验，今天与昨天的湿度差X1及今天的气压差x2是预报明天是否下雨的两个重要因素。

现收集到一批样本数据如下。

今测得x1=0.6，x2=3.0，假定两组的协方差矩阵相等，试用判别分析法预报明天是否会下雨。

解：先编写R程序（程序名：discriminiant.distance.R）discriminiant.distance <- function(TrnX1, TrnX2, TstX = NULL, var.equal = FALSE){if (is.null(TstX) == TRUE) TstX <- rbind(TrnX1,TrnX2)if (is.vector(TstX) == TRUE) TstX <- t(as.matrix(TstX))else if (is.matrix(TstX) != TRUE)TstX <- as.matrix(TstX)if (is.matrix(TrnX1) != TRUE) TrnX1 <- as.matrix(TrnX1)if (is.matrix(TrnX2) != TRUE) TrnX2 <- as.matrix(TrnX2)nx <- nrow(TstX)blong <- matrix(rep(0, nx), nrow=1, byrow=TRUE,dimnames=list("blong", 1:nx))mu1 <- colMeans(TrnX1); mu2 <- colMeans(TrnX2)if (var.equal == TRUE || var.equal == T){S <- var(rbind(TrnX1,TrnX2))w <- mahalanobis(TstX, mu2, S)- mahalanobis(TstX, mu1, S)}else{S1 < -var(TrnX1); S2 <- var(TrnX2)w <- mahalanobis(TstX, mu2, S2)- mahalanobis(TstX, mu1, S1)}for (i in 1:nx){if (w[i] > 0)blong[i] <- 1elseblong[i] <- 2}blong}（注释：在程序中，输入变量表示类TrnX1、类TrnX2训练样本，其输入格式是数据框，或矩阵，输入变量TstX是待测样本，其输入格式是数据框，或矩阵，或向量，如果不输入，则待测样本为两个训练样本之和，即计算两个样本的回代情况。

6-10 今有6个铅弹头，用“中子活化”方法测得7种微量元素的含量数据（见表1）。

(1) 试用多种系统聚类法对6个弹头进行分类；并比较分类结果； (2) 试用多种方法对7种微量元素进行分类。

问题求解1对6个弹头进行分类对数据进行标准化变换，样品间距离定义为欧式距离，系统聚类的方法分别使用类平均法（A VE ）、中间距离法（MID ）、可变类平均法（FLE ）和离差平方合法（WARD ）。

使用SAS 软件CLUSTER 过程对数据进行聚类分析（程序见附录1）。

1.1类平均法图1 类平均聚类法相关矩阵特征值图图2 类平均聚类分析法聚类历史图由图2可知，NCL=1时半偏R 2最大且伪F 统计量在NCL=2,5时和伪t 方统计量在NCL=1,4时较大。

因此，将6个弹头分为两类{}{}(2)(2)121,2,4,6,3,5G G ==。

SAS 绘制的谱系聚类图如图3所示。

图3 类平均聚类分析法谱系聚类图1.2中间距离法图4 中间距离聚类法相关矩阵特征值图图5 中间距离聚类法聚类历史图由图5可知，中间距离法与类平均法结果一致。

因此，也将6个弹头分为两类{}{}(2)(2)121,2,4,6,3,5G G ==。

SAS 绘制的谱系聚类图如图6所示。

图6中间距离聚类法谱系聚类图1.3可变类平均法图7可变类平均聚类法分析结果图图8 可变类平均聚类法聚类历史图由图8可知，可变类平均法(=0.25β-)输出结果与前两种方法稍有不同，NCL=1时半偏R2最大且伪F统计量在NCL=2时次大，NCL=5时最大；而伪t方统计量在NCL=1时最大。

因此，分类结果与之前相同，将6个弹头分为两类{}{}(2)(2)121,2,4,6,3,5G G ==。

SAS 绘制的谱系聚类图如图9所示。

图9 可变类平均聚类法谱系聚类图1.4离差平方和法图10 离差平方和聚类法相关矩阵特征值图图11 离差平方和聚类法聚类历史由图11可知，离差平方和法输出结果与可变类平均法结果一致。

多元统计分析习题集（一）一、填空题1．若()(,),(1,2,,)p X N n αμα∑= 且相互独立，则样本均值向量X 服从的分布是____________________。

2．变量的类型按尺度划分为___________、____________、_____________。

3．判别分析是判别样品_____________的一种方法，常用的判别方法有_____________、_____________、_____________、_____________。

4．Q 型聚类是指对_____________进行聚类，R 型聚类指对_____________进行聚类。

5．设样品12(,,,),(1,2,,)i i i ip X X X X i n '== ，总体(,)p X N μ∑ ，对样品进行分类常用的距离有____________________、____________________、____________________。

6．因子分析中因子载荷系数ij a 的统计意义是_________________________________。

7．主成分分析中的因子负荷ij a 的统计意义是________________________________。

8．对应分析是将__________________和__________________结合起来进行的统计分析方法。

9．典型相关分析是研究__________________________的一种多元统计分析方法。

二、计算题 1．设3(,)X N μ∑ ，其中410130002⎛⎫ ⎪∑= ⎪ ⎪⎝⎭，问1X 与2X 是否独立？12(,)X X '与3X 是否独立？为什么？2．设抽了5个样品，每个样品只测了一个指标，它们分别是1，2，4.5，6，8。

若样品间采用绝对值距离，试用最长距离法对其进行分类，要求给出聚类图。