第4章轴心受力构件的承载力计算

轴心受压构件承载力计算教案一、教学目标：1. 让学生了解轴心受压构件的基本概念及其在工程中的应用。

2. 培养学生掌握轴心受压构件承载力计算的基本原理和方法。

3. 培养学生能够运用所学知识分析和解决实际工程问题。

二、教学内容：1. 轴心受压构件的基本概念1.1 定义及分类1.2 受力特点2. 轴心受压构件承载力计算的基本原理2.1 弹性阶段承载力计算2.2 弹塑性阶段承载力计算2.3 塑性阶段承载力计算3. 影响轴心受压构件承载力的主要因素3.1 材料性质3.2 截面形状3.3 长度3.4 加载方式三、教学方法：1. 采用讲授法，系统地讲解轴心受压构件的基本概念、承载力计算原理及影响因素。

2. 利用案例分析法，让学生通过实际工程案例理解和掌握轴心受压构件的承载力计算方法。

3. 开展小组讨论法，培养学生团队合作精神和解决问题的能力。

四、教学准备：1. 准备相关教材、课件和教学案例。

2. 安排实验室或软件仿真实验，让学生动手实践。

五、教学过程：1. 引入：通过简单的工程实例，引导学生关注轴心受压构件在工程中的重要性。

2. 讲解：系统讲解轴心受压构件的基本概念、承载力计算原理及影响因素。

3. 案例分析：分析实际工程案例，让学生理解和掌握轴心受压构件的承载力计算方法。

4. 实践操作：安排实验室或软件仿真实验，让学生动手实践，加深对知识的理解。

6. 作业布置：布置相关练习题，巩固所学知识。

六、教学评估：1. 课堂讲解：评估学生对轴心受压构件基本概念、承载力计算原理及影响因素的理解程度。

2. 案例分析：评估学生分析实际工程案例的能力，以及是否能正确应用所学知识进行承载力计算。

3. 实践操作：评估学生在实验室或软件仿真实验中的动手能力，以及对实验结果的分析能力。

七、教学反思：1. 针对本节课的教学内容，反思教学方法是否适合学生的学习需求。

2. 反思教学过程中是否存在讲解不清楚或学生理解困难的地方，以便在今后的教学中进行改进。

第四章轴心受力构件的性能与计算1、为什么轴心受拉构件开裂后，当裂缝增至一定数量时，不再出现新的裂缝？答：相邻裂缝之间距离不足以使将混凝土开裂的拉力传递给混凝土。

2、如何确定受拉构件的开裂荷载和极限荷载？答：开裂荷载：混凝土与钢筋的应变达到混凝土的峰值应变。

极限荷载：钢筋达到屈服强度。

3、在轴心受压短柱的短期荷载试验中，随着荷载的增加，钢筋的应力增长速度和混凝土的应力增长速度那个快？为什么？答：钢筋的增长速度快。

钢筋的弹性模量大。

4、如何确定轴心受压短柱的极限承载力？为什么在轴压构件中不宜采用高强钢筋？答：极限承载力：混凝土的应变达到峰值。

当钢筋的抗压强度大于400MPa时，只取400。

5、构件设计时，为什么要控制轴心受力构件的最小配筋率？如何确定轴心受拉和轴心受压构件的最小配筋率？答：为保证所设计的极限承载力大于截面的开裂弯矩，避免在极限状态下出现脆性破坏。

最小配筋率近似等于f t/f y。

6、配有普通箍筋的钢筋混凝土轴心受压构件中，箍筋的作用主要是什么？答：防止纵向钢筋压屈，并与纵筋形成钢筋骨架，使截面中间部分混凝土成为约束混凝土，提高构件的强度和延性。

7、钢筋混凝土轴心受压构件在长期荷载作用下，随着荷载作用时间的增长，钢筋的应力和混凝土的应力各发生什么变化？混凝土的徐变是否会影响短柱的承载力？答：徐变使钢筋的变形也随之变大，钢筋的应力相应地增大，混凝土的应力减小。

8、钢筋混凝土轴心受压构件的承载力计算公式中为什么要考虑稳定系数φ，稳定系数φ与构件两端的约束情况有何关系？答：柱子的长细比对轴心受压强度有较大的影响。

两端铰接：l0=H 一端自由，一端固定：l0=2H一端固定，一端铰接：l0=0.7H 一端固定，一段滑动：l0=0.5H9、为什么长细比l0/b>12的螺旋筋柱，不考虑螺旋筋对柱承载力的有利作用？答：此时的长细比比较大，易发生失稳现象。

10、如箍筋能起到约束混凝土的横向变形作用，则轴心受压短柱的承载力将发生什么变化？为什么？答：承载力将变大。

第4章 思考题参考答案【4-1】为什么轴心受拉构件开裂后，当裂缝增至一定数量时，不再出现新的裂缝？在裂缝处的混凝土不再承受拉力，所有拉力均由钢筋来承担，钢筋通过粘结力将拉力再传给混凝土。

随着荷载的增加，裂缝不断增加，裂缝处混凝土不断退出工作，钢筋不断通过粘结力将拉力传给相邻的混凝土。

当相邻裂缝之间距离不足以使混凝土开裂的拉力传递给混凝土时，构件中不再出现新裂缝。

【4-2】如何确定受拉构件的开裂荷载和极限荷载？（1） 当0t t εε=时，混凝土开裂，这时构件达到的开裂荷载为：000(1)tcr c t c E t N E A E A εαρε==+（2） 钢筋达到屈服强度时，构件即进入第Ⅲ阶段，荷载基本维持不变，但变形急剧增加，这时构件达到其极限承载力为：tu y s N f A =【4-3】 在轴心受压短柱荷载试验中，随着荷载的增加，钢筋的应力增长速度和混凝土的应力增长速度哪个快？为什么？（1）第Ⅰ阶段，开始加载到钢筋屈服。

钢筋增长速度较快。

此时若忽略混凝土材料应力与应变关系之间的非线性关系，则钢筋与混凝土的应力分别为s E ε和c E ε，由于s c E E >，因此钢筋增长的速度较快，若考虑混凝土非线性的影响，此时混凝土应力与荷载关系呈一条上凸的曲线，则钢筋增长的速度相对混凝土更快。

（2）第Ⅱ阶段，钢筋屈服到混凝土被压碎。

混凝土增长速度较快。

当达到钢筋屈服后，此时钢筋的应力保持不变，增加的荷载全部由混凝土承担，混凝土的应力加速增加，应力与荷载关系由原来的上凸变成上凹。

（图4-9）【4-4】如何确定轴心受压短柱的极限承载力？为什么在轴压构件中不宜采用高强钢筋？（1）当00.002εε==时，混凝土压碎，短柱达到极限承载力cu c y s N f A f A ''=+（2）由于当轴压构件达到极限承载力时00.002sεεε'===，相应的纵筋应力值为：32200100.002400/s s s E N mm σε''=≈⨯⨯=由此可知，当钢筋的强度超过2400/N mm 时，其强度得不到充分发挥，因此不宜采用高强钢筋。

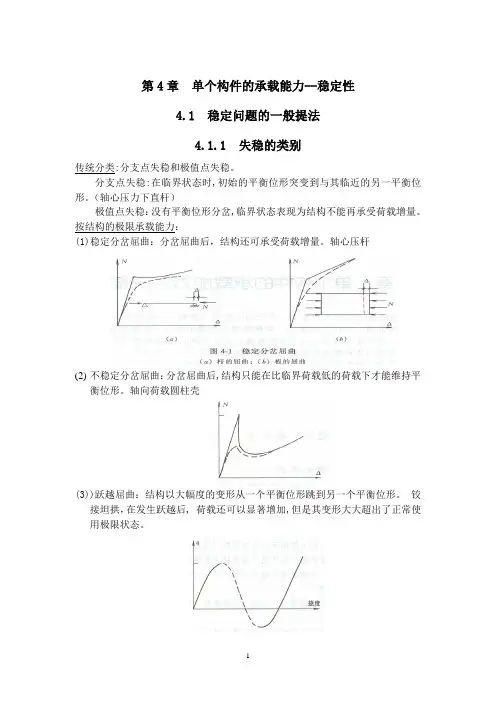
第4章单个构件的承载能力--稳定性4.1 稳定问题的一般提法4.1.1 失稳的类别传统分类:分支点失稳和极值点失稳。

分支点失稳:在临界状态时,初始的平衡位形突变到与其临近的另一平衡位形。

（轴心压力下直杆）极值点失稳：没有平衡位形分岔,临界状态表现为结构不能再承受荷载增量。

按结构的极限承载能力：(1)稳定分岔屈曲：分岔屈曲后，结构还可承受荷载增量。

轴心压杆(2)不稳定分岔屈曲：分岔屈曲后,结构只能在比临界荷载低的荷载下才能维持平衡位形。

轴向荷载圆柱壳(3))跃越屈曲：结构以大幅度的变形从一个平衡位形跳到另一个平衡位形。

铰接坦拱，在发生跃越后, 荷载还可以显著增加,但是其变形大大超出了正常使用极限状态。

4.1.2 一阶和二阶分析材料力学：EI M //1+=ρ 高数：()()2/3222/1///1dx dy dx y d +±=ρ M>0 22/dx y d <0 ； M<0 22/dx y d >0 ；∴ M 与y ''符号相反()()EI M y y /1/2/32-='+''∴ （大挠度理论）当y '与1相比很小时 EI M y /-='' （1） （小挠度理论）不考虑变形，据圆心x 处 ()x h P M --=α1 一阶弯矩 考虑变形 ()()y p x h p M ----=δα2 二阶弯矩 将它们代入（1）式：()x h p y EI -=''α 一阶分析()()y p x h p y EI -+-=''δα 二阶分析边界条件: ()()000='=y y ()δ=h yEI ph 3/3αδ=()()]/)tan(3[)]3/([33kh kh kh EI ph -⨯=αδ （2） EI P k /2=由（2）有 ()∞=--32//)(t a n l i m kh kh kh kh π 得欧拉临界荷载 224/h EI P E π= 此为稳定分析过程：达临界荷载，构件刚度退化为0，无法保持稳定平衡，失稳过程本质上是压力使构件弯曲刚度减小，直至消失。

轴心受压构件正截面承载力计算首先，要计算轴心受压构件的正截面承载力，我们需要了解构件的几何参数，例如截面的尺寸和形状，以及构件的材料特性，如弹性模量和抗压强度等。

下面介绍一种常用的计算方法，即欧拉公式。

欧拉公式适用于细长的杆件，可以计算其承载力。

根据欧拉公式，轴心受压构件的正截面承载力可以表示为：Pcr = (π^2 * E * I) / (Lr)^2其中，Pcr 是构件的临界承载力，E 是构件的弹性模量，I 是构件截面的惯性矩，Lr 是约化长度。

对于不同的构件形状，惯性矩I的计算公式也不同。

以下是一些常见形状的惯性矩计算公式：1.矩形截面：I=(b*h^3)/12，其中b是截面的宽度，h是截面的高度；2.圆形截面：I=π*(d^4)/64，其中d是截面的直径；3.方管截面：I=(b*h^3-(b'*h')^3)/12，其中b是外边框的宽度，h是外边框的高度，b'是内边框的宽度，h'是内边框的高度。

约化长度Lr的计算取决于构件的边界条件。

以下是一些常见边界条件的约化长度计算公式：1.双端固定支承：Lr=L；2.一端固定支承、一端支座支承：Lr=0.7*L；3.双端支座支承：Lr=2*L。

通过使用上述公式，我们可以计算出轴心受压构件的正截面承载力。

需要注意的是，上述公式是基于一些理想化假设和条件下推导得出的，实际工程中还需要考虑一些因素，例如构件的稳定性和局部细部构造等。

因此，在实际设计中，应该根据具体情况综合考虑各种因素，并结合相关的规范和标准进行设计和验证，以确保构件的安全性和可靠性。

总之，轴心受压构件正截面承载力计算是工程设计中的重要环节。

通过合理的参数选择和计算，可以确定构件能够安全承受的最大压力，从而保证结构的安全和可靠性。

第四章轴心受力构件§4-1 概述1、工程实例（假设节点为铰接，无节间荷载作用时，构件只受轴心力作用）（1）桁架（2）塔架（3）网架、网壳2、分类⑴按受力来分：①轴心受拉构件②轴心受压构件到某临界值时，理想轴心受压构件可能以三种屈曲形式丧失稳定。

(1) 弯曲屈曲构件的截面只绕一个主轴旋转，构件的纵轴由直线变为曲线，这是双轴对称截面构件最常见的屈曲形式。

如图4-2 (a)就是两端铰接工字形截面构件发生的绕弱轴的弯曲屈曲。

(2) 扭转屈曲失稳时构件除支承端外的各截面均绕纵轴扭转，图4-2 (b)为长度较小的十字形截面构件可能发生的扭转屈曲。

(3) 弯扭屈曲单轴对称截面构件绕对称轴屈曲时，在发生弯曲变形的同时必然伴随着扭转。

图4-2 (c)即T 形截面构件发生的弯扭屈曲。

图4-2 轴心受压构件的三种屈曲形式欧拉临界力和欧拉临界应力临界应力其中：——单位剪力时的轴线转角，；通常剪切变形的影响较小，忽略其对临界力或临界应力的影响。

E N E σ1222211γλπλπσ⋅⋅+⋅⋅==EAEAN cr cr1γ)(1GA βγ=这样，※上述推导基于材料处于弹性阶段，即，或。

（二）初始缺陷对轴心受压构件稳定承载力的影响 1. 残余应力的影响残余压应力对压杆弯曲失稳的影响： 对弱轴的影响比对强轴的影响要大的多。

稳定应力上限，弱轴：强轴：其中：，0＜＜1.0。

2．初弯曲的影响图4-3 考虑初弯曲的压力—挠度曲线图示压力—挠度曲线有如下特点：1有初弯曲时，挠度v 不是随着N 按比例增加；N 较小时，挠度增加较慢，N 趋于时，挠度增加较快，并趋向于无限大；2相同压力N 的作用下，压杆的初挠度值越大，杆件的挠度也越大；Ecr N EAlEI N =⋅=⋅=2222λππEcr cr E AN σλπσ=⋅==22pcr f E≤⋅=22λπσpp f E λπλ=≥322kEx crx ⋅⋅=λπσkEycry⋅⋅=22λπσ翼缘宽度翼缘弹性区宽度=k k E N3由于有的存在，轴心压杆的承载力总是低于，因此是弹性压杆承载力的上限。

第四章轴心受力构件公式整理1.应变公式：轴心受力构件的应变公式描述了受力构件在轴向受力作用下的变形情况。

应变公式主要有以下两种形式：(1)需要计算伸长形变的情况下：在受力过程中，轴心受力构件发生的伸长形变与受力大小和材料的弹性模量有关。

应变公式可表示为：ε=ΔL/L其中，ε表示轴向应变；ΔL表示受力构件发生的伸长形变；L表示受力构件的初始长度。

(2)不需要考虑伸长形变的情况下：在一些情况下，受力构件的长度相对较短，可以忽略伸长形变的影响。

此时，应变公式可以表示为：ε=δ/h其中，ε表示轴向应变；δ表示构件上其中一截面上的位移；h表示受力构件的高度。

2.应力公式：轴心受力构件的应力公式描述了受力构件在轴向受力作用下的应力分布情况。

应力公式主要有以下两种形式：(1)线性弹性应力公式：在弹性阶段，应力与应变成正比，最常用的应力公式是线性弹性应力公式：σ=E*ε其中，σ表示轴向应力；E表示受力构件材料的弹性模量；ε表示轴向应变。

(2)线性弹塑性应力公式：在考虑弹塑性情况下，应力与应变的关系不再是线性的。

此时，应力公式可以表示为：σ=σe+σp其中，σ表示轴向应力；σe表示弹性应力；σp表示塑性应力。

3.弯矩公式：轴心受力构件在受到弯矩作用时，会引起构件的弯曲变形。

弯矩公式描述了轴心受力构件在弯矩作用下的变形情况。

弯矩公式主要有以下几种形式：(1)切线法公式：根据切线法，弯曲截面上的任意一点都受到一个弯矩的作用。

弯矩公式可以表示为：M=σ*S其中，M表示弯矩；σ表示轴向应力；S表示截面的静矩。

(2)一阶弹性理论公式：在一阶弹性理论中，构件的截面仍然平面，但允许在截面平面上有变形。

弯矩公式可以表示为：M=σ*I/y其中，M表示弯矩；σ表示轴向应力；I表示截面的惯性矩；y表示截面上任一点到中性轴的距离。

(3)符合木尔斯定理的公式：木尔斯定理适用于构件截面受平面弯矩时产生的应力。

弯矩公式可以表示为：M=W*y/I其中，M表示弯矩；W表示截面上的轴向力；y表示截面上任一点到中性轴的距离；I表示截面的惯性矩。

第4章 轴心受力构件例题 4.1 某焊接组合工字形截面轴心受压构件的截面尺寸如图4-13所示，承受轴心压力设计值(包括构件自重)N ＝2000kN ，计算长度l 0y ＝6m ，l 0x ＝3m ，翼缘钢板为火焰切割边，钢材为Q345，截面无削弱。

要求验算该轴心受压构件的整体稳定性是否满足设计要求，并计算整体稳定承载力。

图4—13 焊接工字形截面解 （1）截面及构件几何特性计算A =250×12×2+250×8=8000mm 2I y =(250×2743-242×2503)/12=1.1345×108 mm 4 I x =(12×2503×2+250×83)/12=3.126×107 mm 41.1198000/101345.1/8=⨯==A I i y y mm5.628000/10126.3/7=⨯==A I i x x mmλy =l 0y /i y =6000/119.1=50.4 λx =l 0x /i x =3000/62.5=48.0 (2)整体稳定性验算查表4－5，截面关于x 轴和y 轴都属于b 类，λy >λx1.61235/3454.50235/==y y f λ查附表7得φ=0.80169.31180008016.01020003=⨯⨯=ANϕN/mm 2≈f =310N/ mm 2故可认为整体稳定性满足要求。

（3）整体稳定承载力计算φAf =0.8016×8000×310=1.988×106N=1988kN 该轴心受压构件的整体稳定承载力为1988kN 。

例题4.2 某焊接T 形截面轴心受压构件截面尺寸如图4—14所示。

承受轴心压力设计值(包括构件自重)N ＝2000kN ，计算长度l 0x ＝l 0y ＝3m ，翼缘钢板为火焰切割边，钢材为Q345，截面无削弱。