条件概率青年教师公开课

格式：ppt
大小：1.15 MB
文档页数：25

下载文档原格式

《条件概率公开课》课件

金融分析
学习如何应用条件概率进行金融市场分析和预测。
小结
本节课是对课程内容进行总结和回顾，帮助学习者巩固所学的知识。
1 掌握条件概率的定义和公式
重温条件概率的基本概念，掌握计算方法。
2 理解条件概率的应用
回顾条件概率在医学、风险评估和金融分析等领域的实际应用。
3 提升问题解决能力
通过解决实例问题，提升条件概率的应用能力。
掌握条件概率的计算公式及其应用。
实例演示
通过实例演示，帮助学习者更好地理解条件概率的概念和计算方法。
条件概率的应用
本节课将探讨条件概率在实际生活中的应用，展示它的重要性和普适性。
医学诊断
了解如何使用条件概率来提高医学诊断的准确性和效率。
风险评估
掌握如何使用条件概率评估潜在风险和制定相应的决策。
《条件概率公开课》PPT课件
欢迎参加《条件概率公开课》PPT课件！在本课程中，我们将探讨条件概率的概念、公式、实例和应用。让我们一起深入了解这个有趣且重要的主题吧！Fra bibliotek课件介绍
本节课主要介绍了课程的内容和目标，让学习者对将要学习的知识有一个大致的了解。
概率概念
了解什么是概率以及条件概率的定义。
条件概率公式
了解更多
如果你对条件概率还有更多兴趣，我们提供以下额外资源供你深入学习。
书籍推荐
• 《概率论与数理统计》 • 《概率导论》
在线课程
学术论文
• 华尔街大学：概率与统计 • Coursera：概率与统计基础
• Exploring Conditional Probability in Real-
• W UnodreldrsAtapnpdliicnagtitohnes Fundamentals of Conditional Probability

《条件概率》示范公开课教学课件【高中数学苏教版】

有影响．
若已知事件发生，在事件发生的条件下事件发生的概率是多少？
解：将三个红球分别编号为1，2，3，两个白球分别编号为，，则随机试验“第一次取一个球，不放回，接着第二次取一个球”的样本空间为，，，，，，，，，，，，，，，，，，，．于是，，，，，，，，，，，，，，，，，，，，，．
若已知事件发生，在事件发生的条件下事件发生的概率是多少？
一般地，设，为两个事件，，我们称为事件发生的条件下事件发生的条件概率，记为，读作“发生的条件下发生的概率”，即．
公式仅限于的情况，当时，我们不定义条件概率；在竖线“︱”之后的部分表示条件，须区分与，与．表示事件发生的条件下事件发生的概率，表示事件发生的条件下事件发生的概率；表示事件和事件同时发生的概率，无附加条件．与不一定相等．
若事件，相互独立，即，且，则，这就是说，此时事件发生的概率与已知事件发生的条件下事件发生的概率相等，也就是事件发生与否，不影响事件发生的概率．反过来，若，且，则
，即事件，相互独立．
⇒
由条件概率的计算公式
乘法公式，或，既可以用于求条件概率，也可以用于求两个事件同时发生的概率．
已知，，那么等于( ) A. B. C. D.
解：由概率的乘法公式得．故选B．
假定生男、生女是等可能的，一个家庭中有两个小孩，已知有一个是女孩，则另一个小孩是男孩的概率是 .
解：一个家庭的两个小孩只有4种可能：{男，男}，{男，女}，{女，男}，{女，女}，且所有样本点是等可能的，那么在有一个是女孩的条件下，另一个小孩是男孩的概率为．
第八章概率
条件概率
1.结合古典概型，了解条件概率的定义，能计算简单随机事件的条件概率；2通过韦恩图理解条件概率的计算公式，发展直观想象素养．通过条件概率公式的推导及运用，发展逻辑推理和数学运算素养．

条件概率公开课

实现
首先，根据训练数据集学习HMM的参数，包括初始状态概率、状态转移概率和观测概率；然后，对于给定的观测序列，使用Viterbi算法或前向-后向算法计算最可能的状态
序列。
条件随机场（CRF）模型原理及实现
原理
条件随机场是一种判别式概率模型，用于在给定一组输入特征的情况下预测输出序列。CRF通过定义一组势函数来描述输出序列中各个元素之间的依赖关系。
在分类、回归等任务中，利用条件概率模型对数据进行建模和预测。
D
02 条件概率计算方法
直接计算法
定义法
根据条件概率的定义，直接计算事件 A在事件B发生的条件下的概率，即 P(A|B) = P(AB) / P(B)。
适用范围
适用于事件B的概率P(B) > 0，且事件 A和事件B同时发生的概率P(AB)可以直接计算或通过实验获得的情况。
乘法公式法
乘法公式
利用条件概率的乘法公式P(AB) = P(A) * P(B|A)或P(AB) = P(B) * P(A|B)来计算条件概率。
适用范围
适用于已知其中一个事件的概率和另一个事件在该事件发生的条件下的概率，需要求解两个事件同时发生的概率的情况。
全概率公式法
全概率公式
如果事件B1, B2, ..., Bn构成一个完备事件组，且它们的概率之和为1，则对任一事件A，有P(A) = Σ P(Bi) * P(A|Bi)，其中i=1,2,...,n。
实现
首先，根据训练数据集学习CRF的参数，包括势函数的权重；然后，对于给定的输入特征序列，使用动态规划算法（如Viterbi算法）找到使得势函数之和最大的输出序列。
条件概率在金融风险评估中应
05

2.2.1条件概率公开课2

解 {(男, 男), (男, 女), (女, 男), (女, 女)}
A={已知一个是女孩}＝{(男, 女), (女, 男), (女, 女)}
B {另一个也是女孩} {(女, 女)}
1 所以所求概率为 . 3
课堂练习
掷两颗均匀骰子,已知第一颗掷出6点条件下，问“掷出点数之和不小于10”的概率是多少?

P( AB) P( B) P( B A) 0.8 P( A) P( A)
B
5
0.56
0.7
A
2.条件概率计算公式:
P(B |A)=
P AB P A
注 : ⑴ 0 ≤ P ( B | A) ≤ 1 ; ⑵ 几何解释 : ⑶ 可加性：如果 B和 C 互斥，那么 P ( B C ) | A P ( B | A) P (C | A)
B
A
问题一个家庭中有两个孩子，已知其中有一个是女孩，问这时另一个小孩也是女孩的概率为多大？
例 4 某种动物出生之后活到20岁的概率为0.7，活到
25岁的概率为0.56，求现年为20岁的这种动物活到25 岁的概率。解设A表示“活到20岁”(即≥20)，B表示 “活到25岁” (即≥25) 则 P( A) 0.7, P( B) 0.56
由于B A故A B B，
所求概率为
学中奖的概率吗？缩小了样本空间，基本事件总数减少了

探究三
A 1 (1)事件A：甲站在排头的概率； p( A) A 4 3 A3 1 (2)事件B：乙站在排尾的概率； p( B ) 4 A4 4 2 A2 1 (3)事件A、B同时发生的概率；p( A B) 4 A4 12

条件概率(公开课)

法三：第一次抽到理科题，则还剩下两道理科、两道文科题，故第二次抽到理科题的概率为： 1 C2 1 P( B A) 1 C4 2
规律总结：问题4：谈谈你怎样判断条件概率的： 1、在……条件(前提)下，求……的概率； 2、当已知事件的发生影响所求事件的概率，一般也认为是条件概率。问题5：谈谈你求解条件概率的一般步骤：（1）用字母表示有关事件: （2）求n(AB),n(A)或P(AB),P(A)
P(B |A)：相当于把Ａ看作新的基本事件空间
例1：在5道题中有3道理科题和2道文科题，如果不放回地依次抽取2道题，求：（1）第一次抽取到理科题的概率；（2）第一次和第二次都抽取到理科题的概率；
解：设第1次抽到理科题为事件A，第2次抽到理科题为事件B，则第1次和第2次都抽到理科题为事件AB. （1）从5道题中不放回地依次抽取2道的事件数为
n() A 20
2 5
根据分步乘法计数原理，n( A) A A 12 n( A) 12 3 P ( A) n( ) 20 5
1 3 1 4
例1、在5道题中有3道理科题和2道文科题，如果不放回地依次抽取2道题，求：（1）第一次抽取到理科题的概率；（2）第一次和第二次都抽取到理科题的概率；
（3）利用条件概率公式求
P ( AB) n( AB) P B A P ( A) n( A)
难点突破：
问题6：说出概率 P(B|A)与P(AB)的区别与联系
P( AB) 表示在样本空间中, 计算 AB发生的概率, 而 P(B A ) 表示在缩小的样本空间 A 中, 计算 B 发生的概率.用古典概率公式, 则 AB 中样本点数 P( B A ) , A 中样本点数 AB 中样本点数 P( AB) 中样本点数一般来说, P(B A ) 比 P( AB) 大.

《条件概率》公开课课件

-1-
PA PB ＋＝ PD PD
13 ＝ . 58
栏目链接
13 所以他获得优秀成绩的概率是 . 58 点评：本题条件多，所设事件多，要分清楚事件之间的关系及谁是条件，同时利用公式 P(B∪C|A)＝ P(B|A)＋ P(C|A)可使有些条件概率的计算较为简捷，但应注意这个性质在“B 与 C 互斥”这一前提下才成立．
11 21 31 41 51 12 22 32 42 52 13 23 33 43 53 14 24 34 44 54 15 25 35 45 55 16 26 46 56 61 62 63 64 65 66
练一练
用几何图形怎么解释？ 36 如何规范解答？ B
A∩B
A
61
62
63
64
65
66
解：设Ω 为所有基本事件组成的全体，“第一颗掷出6点”为事件A， “掷出点数之和不小于10”为事件B,则“已知第一颗掷出6点，掷出点数之和不小于10”为事件AB
)
书山勤为径，学海乐做舟，乘风破浪会有时，直挂云帆济沧海!
-1-
-1-
变式训练
2．抛掷红、黄两枚骰子，当红色骰子的点数为 4 或 6 时，两颗骰子的点数之积大于 20 的概率是( 1 1 1 3 A. B. C. D. 4 3 2 5
解析：记 A＝{抛掷两颗骰子，红色骰子的点数为 4 或 6}， B＝{两颗骰子的点数之积大于 20}，则所求概率为 P(B|A)． 12 1 4 1 PAB 1 1 P(A)＝＝，P(AB)＝＝，所以 P(B|A)＝＝ ÷＝ 36 3 36 9 PA 9 3 1 .故选 B. 3 答案：B
AB 的概率 P(A) 和P(AB)可以表P(B|A）吗？

《条件概率公开课》课件

条件概率在贝叶斯网络中的应用
在贝叶斯网络中，条件概率用于描述随机变量之间的依赖关系，以及在给定父节点状态下子节点的概率分布。
条件概率与隐马尔可夫模型
隐马尔可夫模型简介
隐马尔可夫模型是一种统计模型，用于描述一个隐藏的马尔可夫链生成的状态序列和观测序列。
条件概率在隐马尔可夫模型中的应用
在隐马尔可夫模型中，条件概率用于描述在给定隐藏状态下的观测状态概率，以及状态
在日常生活中的应用
医学诊断
在医学诊断中，我们常常需要计算在给定某些症状下患某种疾病的可能性，这需要用到条件概率
。
法律审判
在法律审判中，我们常常需要计算在给定某些证据下被告人有罪或无罪的条件概率，以便做出公
正的裁决。
市场营销
在市场营销中，我们常常需要计算在给定某些购买行为下顾客再次购买的可能性，这需要用到条
学习效率和性能。
条件概率的未来展望
1 2
跨领域应用
随着大数据和机器学习的普及，条件概率的应用领域将越来越广泛，例如自然语言处理、生物信息学、金融等领域。
理论完善
随着应用的深入，条件概率的理论基础也需要不断完善和发展，以更好地指导实际应用。
3
教育推众对其的认识和应用能力，也是未来值得关注的问题。
在机器学习中的应用
分类器设计
强化学习
在分类问题中，我们常常需要计算某个样本属于某个类别的条件概率，以便做出正确的分类决策。
在强化学习中，我们常常需要计算在给定状态下采取某个行动的条件概率，以便更好地选择最优行动。
聚类分析
在聚类分析中，我们常常需要计算在给定聚类结果下各个样本属于某个聚类的条件概率，以便更好地评估聚类效果。

条件概率公开课ppt课件

THANKS
感谢观看
语言模型
在自然语言处理中，语言模型是非常重要的组成部分，而贝叶斯定理可以在语言模型中发挥重要作用，例如在n-gram模型中计算词的概率。
05
条件概率在统计学中地位和作用
条件概率在假设检验中作用
1 2 3
确定原假设和备择假设
基于条件概率，可以明确假设检验中的原假设和备择假设，进而构建检验统计量。
相关性分析应用
相关性分析在信号处理中广泛应用于噪声抑制、信号检测、模式识别等领域。例如，在语音识别中，通过对语音信号进行相关性分析，可以提取出语音特征参数用于识别不同的语音内容。
04
贝叶斯定理及其应用
贝叶斯定理基本形式
条件概率公式
$P(AB) = P(A)P(B/A) = P(B)P(A/B)$
相互独立的事件之间不具有相互影响，因此一个事件的发生不会改变另一个事件的发生概率。但是需要注意的是，独立事件和互斥事件是不同的概念，互斥事件不能同时发生，但独立事件可以。
条件概率计算方法
条件概率的计算方法主要有两种：一种是利用条件概率的定义直接计算，即P(A|B)=P(AB)/P(B)；另一种是利用全概率公式进行计算，特别适用于事件B可以划分为多个互斥事件的并集的情况。
。条件概率在泊松过程中用于描述在已知某个事件发生的情况下，其他
事件发生的概率。
03
布朗运动
布朗运动是一种连续时间的随机过程，用于描述微粒在液体或气体中的
无规则运动。条件概率在布朗运动中用于描述微粒在未来某个时刻的位
置分布。
03
多元随机变量条件概率
多元随机变量联合分布
联合分布函数定义
对于多元随机变量$(X_1, X_2, ..., X_n)$，其联合分布函数$F(x_1, x_2, ..., x_n)$描述了随机变量取值小于等于$(x_1, x_2, ..., x_n)$的概率。

04394_《条件概率》公开课教学PPT课件

2024/1/24
诊断试验评估
利用条件概率评估诊断试验的准确性，如灵敏度、特异度等。
疾病预后评估
根据患者的病史、症状等信息，预测疾病的发展趋势和预后情况。
16
金融风险评估中的应用
信用评分
基于借款人的历史信用记录和其他信息，评估其未来违约的可能性。
2024/1/24Fra bibliotek市场风险评估
分析市场因素（如利率、汇率等）对投资组合价值的影响。
• 与条件概率的联系与区别：条件期望和条件方差都是基于条件概率的概念进行定义的，但它们描述的是随机变量在某一条件下的不同特征。条件概率描述的是事件发生的可能性，而条件期望和条件方差则分别描述随机变量的平均值和波动情况。
2024/1/24
25
THANKS
感谢观看
2024/1/24
26
概率分布。
22
应用领域
广泛应用于分类、聚类、预测等任务，如自然语言处理、图像处理、
医学诊断等。
06
总结回顾与拓展延伸
2024/1/24
23
关键知识点总结回顾
2024/1/24
条件概率的定义与性质
条件概率是指在某一事件发生的条件下，另一事件发生的概率。它具有非负性、规范性、可加性等基本性质。
2024/1/24
条件概率反映了事件之间的依赖关系，是概率论中的重要概念。
条件概率的计算公式为： P(B|A) = P(AB) / P(A)，其中 P(AB)表示事件A和事件B同时发生的概率，P(A)表示事件A 发生的概率。
4
概率论与数理统计关系
概率论是研究随机现象数量规律的数学分支，而数理统计则是应用概率论对随机现象进行推断和分析的数学分支。

《条件概率》教案.doc

《条件概率》教案新课起航一、我们的目标定位：(1)理解条件概率的定义(2)掌握条件概率的计算方法(3)能解决条件概率相应一些的问题二、重点难点：【教学重点】： 1．条件概率的计算方法。

2．条件概率的应用。

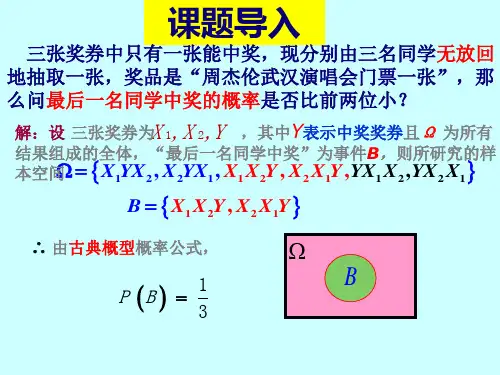
【教学难点】：条件概率的应用三、我们一起来研究（一）课题引入小游戏：摸球3 个兵乓球， 2 个白色的，１个黄色的，现分别由三名同学无放回地抽取一个，摸到黄色的就中奖。

1、请问最后一名同学中奖的概率是否比第一位小？2、如果已经知道第一名同学没中奖，那么最后一名摸球同学的中奖的概率是多少？（二）新课探究1、条件概率的定义：一般的设A， B 为两个事件，且P(A)>0 ，P(B|A) 为在事件 A 发生的条件下，事件 B 发生的 ________.其中 P(B|A) 读作 ___________________P(A|B) 的含义是什么？2、条件概率的性质：（1）有界性： ______________________（2）可加性： ______________________3、条件概率的计算合作探究：根据上面摸奖的例子，想一想怎样求条件概率？你能否得到求条件概率的公式？请合作解决（ 1）利用古典概型计算（）P(B|A)=_________________关键：_____________________（ 2）利用公式计算（）P(B|A)= _________________关键：_____________________4、概率P(B|A) 与 P(AB) 的区别与联系P(AB)P(B|A)联系事件发生区顺序别样本空间大小(三 )应用与探索【例 1】在 5 道题中有 3 道理科题和 2 道文科题。

如果不放回地依次抽取 2 道题，求：(1)第 1 次抽到理科题的概率；(2)第 1 次和第 2 次都抽到理科题的概率；(3)在第 1 次抽到理科题的条件下，第 2 次抽到理科题的概率。

求解条件概率的一般步骤:【巩固练习1】（ 1）掷两颗骰子（ 2）掷两颗骰子,求“已知第一颗为 6 点，则掷出点数之和不小于,求“已知掷出点数之和不小于 9,则第一颗掷出9”的概率6 点”的概率【巩固练习2】甲乙两地都位于长江下游，根据一百多年的气象记录，知道甲乙两地一年中雨天所占的比例分别为 20％和 18％，两地同时下雨的比例为 12％，问：（1）乙地为雨天时甲地也为雨天的概率是多少？（2）甲地为雨天时乙地也为雨天的概率是多少？【例 2】大脑细胞中的NPTN 基因变异会导致天才的出现，平度一中连年取得高考佳绩引起了科学家的注意，现从我校含有 5 名 NPTN 基因变异的 20 名同学中任意选择两位，其中一人经测定为 NPTN 基因变异，求此二人都是 NPTN 基因变异的概率我们的收获一、基本知识上：二、思想方法上：课后作业1、课后第54 页练习，习题 A 组2、3、42.50 件产品中有 3 件次品，不放回的抽取两次，每次抽取一件，已知第一次抽出的是次品，第二次抽出的也是次品的概率是（）3 6 6 2A. 50B. 1225C.25D.493.教室里有 3 名男同学和 5 名女同学，从中随机依次走出两名同学，如第一次走出的是一名女同学，则第二次走出的是一名男同学的概率为___________.第二次走出的仍是一名女同学的概率为 _____________.4.一个家庭中有两个孩子，假定生男、生女是等可能的，已知这个家庭中有一个孩子是女孩，问这时另一个孩子是男孩的概率是__________.5.一张储蓄卡的密码共有 6 位数字，每位数字都可从0～ 9 中任选一个，某人在银行自动提款机上取钱时，忘记了密码的最后一位数字，求（ 1）任意按最后一位数字，不超过 2 次就按对的概率；（ 2）如果他记得密码的最后一位是偶数，不超过 2 次就按对的概率。

条件概率(公开课)课件

在决策理论中的应用
决策树
决策树是一种表示决策过程的方法，其中条件概率用于计算每个决策节点的收益和损失。
贝叶斯决策理论
贝叶斯决策理论利用条件概率来计算期望值和风险，从而选择最优的决策。
强化学习
强化学习中，条件概率用于描述状态转移和奖励函数，帮助智能体在环境中做出最优决策。
在机器学习中的应用
条件概率(公开课)课件
目录
• 条件概率的定义与性质 • 条件概率的计算 • 条件概率的应用 • 条件概率的扩展 • 条件概率的注意事项
01
条件概率的定义与性质
定义
条件概率的定义
在某个事件B已经发生的情况下，另一个事件A发生的概率，记作P(A|B) 。
条件概率的数学表达式
P(A|B) = P(A∩B) / P(B)，其中P(A∩B) 表示事件A和事件B同时发生的概率， P(B)表示事件B发生的概率。
01
分类器
分类器利用条件概率来计算给定输入属于某个类别的概率，常用的分类
器有朴素贝叶斯分类器和逻辑回归分类器。
02
聚类分析
聚类分析中，条件概率可以用于相似性度量和距离计算，常用的聚类算
法有K-means和层次聚类。
03
自然语言处理
在自然语言处理中，条件概率被广泛用于词向量表示、语言模型、情感
分析等任务中，例如使用循环神经网络（RNN）或长短期记忆网络
在实际应用中，有时候很难获取到足够的数据来进行准确的条件概率计算。
THANKS
感谢观看
如果两个事件是独立的，那么它们的条件概率等于它们各自的概率。
如果两个事件不是独立的，那么它们的条件概率会受到其他事件的影响，不能简单地使用各自的概率来计算。

条件概率(公开课)课件

条件概率的公式
P(A|B) = P(A∩B) / P(B)，其中P(A∩B)表示事件A和事件B同时发生的概率，P(B) 表示事件B发生的概率。
条件概率的性质
非负性
条件概率P(A|B)是非负的，即P(A|B) ≥ 0。
归一性
在给定事件B发生的条件下，事件A发生的概率加上事件A不发生的概率等于1，即P(A|B) + P(¬A|B) = 1。
总结词
应用场景
在使用全概率公式时，需要确保每个构成事件的概率之和为1，即Σ P(Bi) = 1。
注意事项
全概率公式广泛应用于各种领域，如天气预报、市场调查、交通规划等，用于分析多个因素对结果的影响。
贝叶斯公式
总结词
贝叶斯公式用于在已知先验概率和条件概率的情况下，计算后验概率。
应用场景
贝叶斯公式广泛应用于各个领域，如自然语言处理、机器学习、统计学等，用于更新和调整事件的概率估计。
01
深度学习是一种机器学习技术，通过构建多层神经网络来学习复杂数据的内在规律和表示。条件概率在深度学习中用于描述不同层之间的连接关系和数据特征的依赖性。
02
在深度神经网络中，条件概率通常用于定义前一层的输出作为下一层输入的条件。这种条件概率关系使得网络能够学习数据特征之间的依赖性和层次结构。
注意事项
使用乘法规则时需要注意确保分母不为零，即事件B发生的概率不能为零。
全概率公式
全概率公式用于计算复杂事件发生的概率，通过将其分解为若干个简单事件的概率之和。
输入标题
详细描述
全概率公式是将一个复杂事件A的概率表示为其构成事件的概率之和，即P(A) = Σ P(Bi) * P(A | Bi)，其中 Bi是构成事件A的各个基本事件。

条件概率公开课一等奖市赛课获奖课件pptx

2024/1/27
条件概率的公式为P(A|B) = P(AB) / P(B)，其中P(AB)表示事件A和事件B同时发生的概率， P(B)表示事件B发生的概率。
条件概率公式是计算条件概率的基本方法，通过该公式可以求得任意两个事件之间的条件概率。
在实际应用中，条件概率公式常常与全概率公式和贝叶斯公式一起使用，以解决更为复杂的概率问题。
通过本次课程的学习，学生们学会了如何有效地学习概率论与数理统计等相关课程，包括课前预习、课后复习、独立思考和合作学习等方法。
2024/1/27
23
对未来研究的展望
2024/1/27
拓展应用领域
随着大数据时代的到来，条件概率在数据分析、机器学习、人工智能等领域的应用将更加广泛。未来研究可以进一步探索条件概率在这些领域中的新应用和新方法。
条件概率公开课一等奖市赛课获奖课件
pptx
2024/1/27
1
目录
2024/1/27
• 引言 • 条件概率基本概念 • 条件概率计算方法 • 条件概率在生活中的应用 • 条件概率与贝叶斯公式关系探讨 • 总结与展望
2
01
引言
2024/1/27
3
课件背景与目的
课件背景
条件概率是概率论中的重要概念，广泛应用于统计推断、机器学习等领域。本次公开课旨在帮助学生深入理解条件概率的概念、性质和应用，提高学生的数学素养和解决实际问题的能力。
2024/1/27
13
04
条件概率在生活中的应用
2024/1/27
14
医学诊断中的应用
01 疾病筛查
利用条件概率评估某种症状下疾病发生的可能性，如乳腺癌筛查中的阳性预测值。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

解：设第1次抽到理科题为事件A，第2次抽到理科题为事件B，则第1次和第2次都抽到理科题为事件AB.
（2） n( AB) A 6
2 3
n( AB ) 6 3 P ( AB ) n( ) 20 10
例1：在5道题中有3道理科题和2道文科题，如果不放回地依次抽取2道题，求：（1）第一次抽取到理科题的概率；（2）第一次和第二次都抽取到理科题的概率；
P ( AB ) P( A | B ) P( A )
Ω
B
A
A
P(B |A)相当于把Ａ看作新的基本事件空间求Ａ∩Ｂ发生的概率
(3)条件概率的加法公式若B和C是两个互斥事件, 则 P( B C A) P( B A) P(C A)
易错概念辨析
概率 P(B|A)与P(AB)的区别与联系
P( AB) 表示在样本空间中, 计算 AB发生的概率, 而 P( B A) 表示在缩小的样本空间 A 中, 计算 B 发生的概率.用古典概率公式, 则 AB 中样本点数 P( B A) , A 中样本点数 AB 中样本点数 P( AB) 中样本点数一般来说, P( B A) 比 P( AB) 大.
练习：课本P54练习1
反思
求解条件概率的一般步骤：
（1）用字母表示有关事件
（2）求P(AB），P(A)或n(AB),n(A)
( 3 )利用条件概率公式求
P ( AB) n( AB) P B A P ( A) n( A)
条件概率计算中注意的问题 1、条件概率的判断：（1）当题目中出现“在……前提（条件）下”等字眼，一般为条件概率。（2）当已知事件的发生影响所求事件的概率，一般也认为是条件概率。 2、相应事件的判断：
2. 事件 A与 B都发生的事件叫做 A与 B的积事件 , 记为 A B (或 AB ); 3.互斥事件：事件A、B不能同时发生当A、B互斥时，
P(AB) P(A) P （ B）
情景引入
三张奖券中只有一张能中奖，现分别由3名同学无放回地抽取，问最后一名同学抽到中奖奖券的概率是否比前两位小？
例2 一张储蓄卡的密码共有6位数字，每位数字
（1）任意按最后一位数字，不超过2次就按对的概率；
都可从0—9中任选一个。某人在银行自动取款机上取钱时，忘记了密码的最后一位数字，求：
（2）如果他记得密码的最后一位是偶数，不超过2次就按对的概率。
1 91 1 (1) P( A) P( A1 ) P( A1 A2 ) 10 10 9 5 1 41 2 (2) P( A | B) P( A1 | B) P( A1 A2 | B ) 5 54 5
由古典概型可知，最后一名同学抽到中奖奖券的 n( B ) 1 概率为：P ( B ) n( ) 3
一般地，我们用来表示所有基本事件的集合，叫做基本事件空间（或样本空间）
如果已经知道第一名同学没有中奖，那么最后一名同学中奖的概率是多少？
问题2:
事件A已经发生，只需在A的范围内考虑问题即可，我们记此时的事件空间为 A ，则
条件概率 Conditional Probability
1、定义一般地,设Ａ，Ｂ为两个事件, 且Ｐ（A）＞０，称
P ( AB ) P ( B A) P ( A)
为在事件A发生的条件下，事件B下 B 的概率。
2.条件概率计算公式:
注:⑴ 0 ≤ P( B | A) ≤1 ; ⑵几何解释:
思考
• 为什么两个问题的概率不一样？
因为探究中已知第一名同学的抽奖结果会影响最后一名同学抽到中奖奖券的概率。若记A:第一名同学没有抽到中奖劵，一般地，在已知事件A发生的前提下，事件B发生的可能性大小不一定再是P(B).我们将探究中的事件记为 P ( A B ) ,称为在“A已发生”的条件下，B发生的条件概率
首先用相应的字母A、B表示出相应的事件，然后分析清楚在哪个事件发生的条件下求哪个事件的概率。
当A B时，P(AB)=P(A)
1. 条件概率的定义. 2. 条件概率的计算. 公式:
P ( AB ) P ( B A) P ( A)
作业布置
• 习题2.2A组T2 • 课时练P38练习3
Thank you!
A X1X2Y, XYX 1 2, X2XY 1 , X2YX 1
知道第一名同学的结果会影响最后一名同学中奖的概率吗？
在事件A发生的情况下，事件B发生等价于事件A和事件B同时发生，即事件AB发生，而事件AB中含有两个事件，即
A BXXY 1 2 , XXY 2 1
• 由古典概型可知，
n AB 2 P( B A) 4 n A
另一方面，运用概率公式，我们容易得到
n AB P(B A) n A n AB n P AB n A P A n
因此我们可以通过事件A和事件AB 的概率来表示 P ( B A )
小组探究：
问题1:如果记最后一名同学抽到中奖奖券的事件为事件B，那么事件B发生的概率是多少？问题2: 如果已经知道第一名同学没有抽到中奖奖券,那么最后一名同学抽到奖券的概率又是多少？问题3：你计算的结果一样吗？若不一样,为什么?
三张奖券中只有一张能中奖，现分别由3名同学无放回地抽取，问最后一名同学抽到中奖奖券的概率是否比前两位小？
（3）在第一次抽到理科题的条件下，第二次抽到理科题的概率。
法一：由（1）（2）可得，在第一次抽到理科题的条件下，第二次抽到理科题的概率为
3 P( AB) 10 1 P( B A) 3 2 P( A) 5
法二：因为n(AB)=6，n(A)=12，所以
n( AB) 6 1 P( B A) n( A) 12 2
2.2.1 条件概率
高二数学组 xxx 2015-05
学习目标
• 了解条件概率的定义 • 掌握条件概率的计算方法 • 会利用条件概率公式解决一些简单的实际问题
• 重点&难点
• 条件概率的概念的理解 • 灵活运用条件概率公式解决简单实际问题
复习旧知：
1.事件A与B至少有一个发生的事件叫做A与B的和事件,记为 A B (或 A B );
例1：在5道题中有3道理科题和2道文科题，如果不放回地依次抽取2道题，求：（1）第一次抽取到理科题的概率；（2）第一次和第二次都抽取到理科题的概率；
解：设第1次抽到理科题为事件A，第2次抽到理科题为事件B，则第1次和第2次都抽到理科题为事件AB.
（1）从5道题中不放回地依次抽取2道的事件数为
解：记“最后一名同学中奖”为事件B Ω 为所有结果组成的全体
X 1 X 2Y , X 1YX 2 , YX 1 X 2 , X 2 X 1Y , X 2YX 1 , YX 2 X 1 B X 1 X 2Y , X 2 X 1Y
一般地，n(B)表示事件B包含的基本事件的个数
n() A 20
2 5
根据分步乘法计数原理，n( A) A A 12 n( A) 12 3 P ( A) n( ) 20 5
1 3 1 4
例1、在5道题中有3道理科题和2道文科题，如果不放回地依次抽取2道题，求：（1）第一次抽取到理科题的概率；（2）第一次和第二次都抽取到理科题的概率；

条件概率青年教师公开课

合集下载

《条件概率公开课》课件

《条件概率》示范公开课教学课件【高中数学苏教版】

条件概率公开课

2.2.1条件概率公开课2

条件概率(公开课)

《条件概率》公开课课件

《条件概率公开课》课件

条件概率公开课ppt课件

04394_《条件概率》公开课教学PPT课件

《条件概率》教案.doc

条件概率(公开课)课件

条件概率(公开课)课件

条件概率公开课一等奖市赛课获奖课件pptx

文档推荐

最新文档