清华大学高等数值分析实验设计及答案
- 格式:doc
- 大小:305.00 KB
- 文档页数:13

1.用Gauss 消去法解方程组⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤---⎢⎢⎢⎢⎣⎡-551631011411014211264321x x x x 解:第一步:交换第三行和第一行,得到如下矩阵⎥⎥⎥⎥⎦⎤----⎢⎢⎢⎢⎣⎡-56153101111402411621做运算()22121E E E →⎪⎭⎫ ⎝⎛+-,()33161E E E →⎪⎭⎫⎝⎛+-,()()441E E E →+,得到增广矩阵 ⎥⎥⎥⎥⎦⎤------⎢⎢⎢⎢⎣⎡0249525213237414210001 第二步:再做运算()3322E E E →+,()44221E E E →⎪⎭⎫⎝⎛+-,得到如下矩阵 ⎥⎥⎥⎥⎦⎤-----⎢⎢⎢⎢⎣⎡94295292113377400210001第三步:做运算()4433713E E E →⎪⎭⎫⎝⎛+,得到 ⎥⎥⎥⎥⎦⎤------⎢⎢⎢⎢⎣⎡21342951919210377400210001利用回代公式求得.790576.0,361257.0,863874.0,115183.11234=-==-=x x x x2、解 2.51 1.48 4.531.480.93 1.302.68 3.041.48⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦123x x x ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=0.051.030.53⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦ 做两次换行()()()()↔↔3132;E E E E 得2.683.04 1.42.511.48 4.531.480.931.30⎡⎤-⎢⎥⎢⎥⎢⎥-⎣⎦123x x x ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=0.530.051.03⎡⎤-⎢⎥⎢⎥⎢⎥⎣⎦ 计算()()()()-+→-+→1221330.93657;0.55224;E E E E E E2.683.04 1.481.3672 5.916100.748810.48269⎡⎤-⎢⎥-⎢⎥⎢⎥--⎣⎦123x x x ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=0.530.546381.3227⎡⎤-⎢⎥⎢⎥⎢⎥⎣⎦计算()()-+→2330.54770;E E E2.683.04 1.4801.36725.9161003.7229⎡⎤-⎢⎥-⎢⎥⎢⎥-⎣⎦123x x x ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦=0.530.546381.0235⎡⎤-⎢⎥⎢⎥⎢⎥⎣⎦ 换行和消去到此结束,经回代计算得到x =()1.440360, 1.577963,0.27494T--3.用Doolittle 三角分解方法解方程组⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----551631011411014211264321x x x x解:首先对系数矩阵A 做分解LUA =解出:解b y L=,计算出Ty ⎪⎭⎫ ⎝⎛--=74213,521,1,6解y x U=,计算出()T x 115183.1,863874.0,361257.0,790576.0--=4.设][,ij n n a A R A =∈⨯,011≠a ,b Ax =经过高斯消去法一步后变为)2()2(b x A =,其中=)2(A⎥⎦⎤⎢⎣⎡21110A a a T ,(2)A =()(2),2n ij i j a =为(n-1)⨯(n-1)矩阵.其元素为(2)ija =(1)ij a -(1)(1)11i j a a /(1)11a , ,i j =2,3, n. 证明:(1)若A 对称正定,则2A 是对称矩阵。

第一章 绪论(1)1.设0x >,x 的相对误差为δ,求ln x 的误差。
解:近似值*x 的相对误差为*****r e x x e x x δ-=== 而ln x 的误差为()1ln *ln *ln **e x x x e x =-≈ 进而有(ln *)x εδ≈2.设x 的相对误差为2%,求nx 的相对误差。
解:设()n f x x =,则函数的条件数为'()||()p xf x C f x = 又1'()n f x nx-=, 1||n p x nx C n n-⋅∴== 又((*))(*)r p r x n C x εε≈⋅且(*)r e x 为2((*))0.02n r x n ε∴≈3.下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字:*1 1.1021x =,*20.031x =, *3385.6x =, *456.430x =,*57 1.0.x =⨯ 解:*1 1.1021x =是五位有效数字; *20.031x =是二位有效数字; *3385.6x =是四位有效数字; *456.430x =是五位有效数字; *57 1.0.x =⨯是二位有效数字。
4.利用公式(2.3)求下列各近似值的误差限:(1) ***124x x x ++,(2) ***123x x x ,(3) **24/x x . 其中****1234,,,x x x x 均为第3题所给的数。
解:*41*32*13*34*151()1021()1021()1021()1021()102x x x x x εεεεε-----=⨯=⨯=⨯=⨯=⨯***124***1244333(1)()()()()1111010102221.0510x x x x x x εεεε----++=++=⨯+⨯+⨯=⨯ ***123*********123231132143(2)()()()()1111.10210.031100.031385.610 1.1021385.6102220.215x x x x x x x x x x x x εεεε---=++=⨯⨯⨯+⨯⨯⨯+⨯⨯⨯≈**24****24422*4335(3)(/)()()110.0311056.430102256.43056.43010x x x x x x xεεε---+≈⨯⨯+⨯⨯=⨯=5计算球体积要使相对误差限为1,问度量半径R 时允许的相对误差限是多少? 解:球体体积为343V R π=则何种函数的条件数为23'4343p R V R R C V R ππ===(*)(*)3(*)r p r r V C R R εεε∴≈=又(*)1r V ε=故度量半径R 时允许的相对误差限为1(*)10.333r R ε=⨯≈6.设028Y =,按递推公式1n n Y Y -=(n=1,2,…)计算到100Y 27.982≈(5位有效数字),试问计算100Y 将有多大误差?解:1n n Y Y -=-10099Y Y ∴=-9998Y Y =9897Y Y =-……10Y Y =-依次代入后,有1000100Y Y =-即1000Y Y =27.982, 100027.982Y Y ∴=-*310001()()(27.982)102Y Y εεε-∴=+=⨯100Y ∴的误差限为31102-⨯。
清华大学高等数值分析课程作业第二次实验 作业第一题:构造例子特征值全部在右半平面时,观察基本的Arnoldi 方法和GMRES 方法的数值性态,和相应重新启动算法的收敛性。
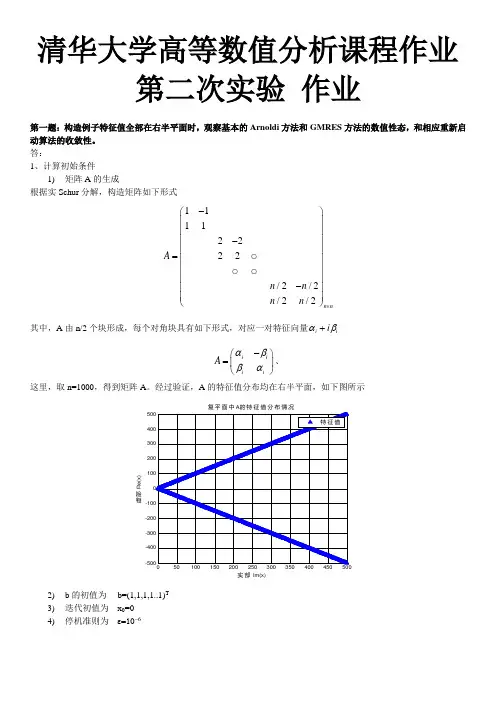
答:1、计算初始条件1) 矩阵A 的生成根据实Schur 分解,构造矩阵如下形式11112222/2/2/2/2n nA n n n n ⨯-⎛⎫ ⎪ ⎪ ⎪- ⎪= ⎪ ⎪ ⎪- ⎪⎪⎝⎭其中,A 由n/2个块形成,每个对角块具有如下形式,对应一对特征向量i i i αβ+ii i i A αββα-⎛⎫= ⎪⎝⎭、 这里,取n=1000,得到矩阵A 。
经过验证,A 的特征值分布均在右半平面,如下图所示50100150200250300350400450500-500-400-300-200-1000100200300400500复平面中A 的特征值分布情况实部 Im(x)虚部 R e (x )特征值2) b 的初值为 b=(1,1,1,1..1)T 3) 迭代初值为 x 0=0 4) 停机准则为 ε=10-62、基本的Arnoldi 和GMRES 方法代入前面提到的初始值A 、b 、x0,得到的收敛结果如下10020030040050060010-710-610-510-410-310-210-110两种基本算法的||r k ||收敛曲线 (阶数n=1000)迭代次数||r k ||/||b ||基本的Arnoldi 算法基本的GMRES 算法结果讨论:从图中可以看出,基本的Arnoldi 方法经过554步收敛,基本的GMRES 方法经过535步收敛。
这是由于GMRES 具有残差最优性,会略快于Arnoldi 方法,但是,由于两种方法的基本原理近似,GMRES 方法不会实质性的提速。
此外,从收敛曲线上看,由于特征值均处在右半平面,收敛曲线平滑,收敛速度(收敛因子)比较均匀。
3、重启动的GMRES 和Arnoldi 算法对上述A 、b 、x0使用重启动的Arnoldi 和GMRES 算法。

数值分析实验报告-清华大学--线性代数方程组的数值解法(总15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--线性代数方程组的数值解法实验1. 主元的选取与算法的稳定性问题提出:Gauss 消去法是我们在线性代数中已经熟悉的。
但由于计算机的数值运算是在一个有限的浮点数集合上进行的,如何才能确保Gauss 消去法作为数值算法的稳定性呢?Gauss 消去法从理论算法到数值算法,其关键是主元的选择。
主元的选择从数学理论上看起来平凡,它却是数值分析中十分典型的问题。
实验内容:考虑线性方程组 n n n R b R A b Ax ∈∈=⨯,,编制一个能自动选取主元,又能手动选取主元的求解线性方程组的Gauss 消去过程。
实验要求:(1)取矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1415157,6816816816 b A ,则方程有解T x )1,,1,1(* =。
取n=10计算矩阵的条件数。
让程序自动选取主元,结果如何?(2)现选择程序中手动选取主元的功能。
每步消去过程总选取按模最小或按模尽可能小的元素作为主元,观察并记录计算结果。
若每步消去过程总选取按模最大的元素作为主元,结果又如何?分析实验的结果。
(3)取矩阵阶数n=20或者更大,重复上述实验过程,观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异,说明主元素的选取在消去过程中的作用。
(4)选取其他你感兴趣的问题或者随机生成矩阵,计算其条件数。
重复上述实验,观察记录并分析实验结果。
程序清单n=input('矩阵A 的阶数:n=');A=6*diag(ones(1,n))+diag(ones(1,n-1),1)+8*diag(ones(1,n-1),-1); b=A*ones(n,1);p=input('计算条件数使用p-范数,p='); cond_A=cond(A,p) [m,n]=size(A);Ab=[A b];r=input('选主元方式(0:自动;1:手动),r=');Abfor i=1:n-1switch rcase(0)[aii,ip]=max(abs(Ab(i:n,i)));ip=ip+i-1;case (1)ip=input(['第',num2str(i),'步消元,请输入第',num2str(i),'列所选元素所处的行数:']);end;Ab([i ip],:)=Ab([ip i],:);aii=Ab(i,i);for k=i+1:nAb(k,i:n+1)=Ab(k,i:n+1)-(Ab(k,i)/aii)*Ab(i,i:n+1);end;if r==1Abendend;x=zeros(n,1);x(n)=Ab(n,n+1)/Ab(n,n);for i=n-1:-1:1x(i)=(Ab(i,n+1)-Ab(i,i+1:n)*x(i+1:n))/Ab(i,i);endx运行结果(1)n=10,矩阵的条件数及自动选主元Cond(A,1) =×103Cond(A,2) = ×103Cond(A,inf) =×103程序自动选择主元(列主元)a.输入数据矩阵A的阶数:n=10计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动),r=0b.计算结果x=[1,1,1,1,1,1,1,1,1,1]T(2)n=10,手动选主元a. 每步消去过程总选取按模最小或按模尽可能小的元素作为主元矩阵A 的阶数:n=10计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动),r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元,请输入第1列所选元素所处的行数:1(2)(2) 6.0000 1.00007.00004.6667 1.0000 5.66678.0000 6.000015.0000[]8.00001.000015.00006.0000 1.00008.0000 6.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元,请输入第2列所选元素所处的行数:2…(实际选择时,第k 步选择主元处于第k 行) 最终计算得x=[, , , , , , , , , ]Tb. 每步消去过程总选取按模最大的元素作为主元 矩阵A 的阶数:n=10计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动),r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元,请输入第1列所选元素所处的行数:2(2)(2)8.0000 6.0000 1.000015.0000-3.50000.7500-4.250008.0000 6.0000 1.000015.0000[]8.0000 6.000015.00008.0000 1.00006.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元,请输入第2列所选元素所处的行数:3…(实际选择时,第k 步选择主元处于第k+1行) 最终计算得x=[1,1,1,1,1,1,1,1,1,1]T(3)n=20,手动选主元a. 每步消去过程总选取按模最小或按模尽可能小的元素作为主元 矩阵A 的阶数:n=20计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动),r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元,请输入第1列所选元素所处的行数:1(2)(2) 6.0000 1.00007.00004.6667 1.0000 5.66678.0000 6.000015.0000[]8.00001.000015.00006.0000 1.00008.0000 6.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元,请输入第2列所选元素所处的行数:2…(实际选择时,第k 步选择主元处于第k 行) 最终计算得x=[,,,,,,,,,,,,,,,,,,,]T b. 每步消去过程总选取按模最大的元素作为主元 矩阵A 的阶数:n=20计算条件数使用p-范数,p=1选主元方式(0:自动;1:手动),r=1(1)(1)61786115[]861158614A b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦第1步消元,请输入第1列所选元素所处的行数:2(2)(2)8.0000 6.0000 1.000015.0000-3.50000.7500-4.250008.0000 6.0000 1.000015.0000[]8.0000 6.000015.00008.0000 1.00006.0000 1.000015.00008.0000 6.000014.0000A b ⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦第2步消元,请输入第2列所选元素所处的行数:3…(实际选择时,第k步选择主元处于第k+1行)最终计算得x=[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]T(4)A分别为幻方矩阵,Hilbert矩阵,pascal矩阵和随机矩阵简要分析计算(1)表明:对于同一矩阵,不同范数定义的条件数是不同的;Gauss消去法在消去过程中选择模最大的主元能够得到比较精确的解。


数值分析实验报告一、 实验3。
1 题目:考虑线性方程组b Ax =,n n R A ⨯∈,n R b ∈,编制一个能自动选取主元,又能手动选取主元的求解线性代数方程组的Gauss 消去过程。
(1)取矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=6816816816 A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1415157 b ,则方程有解()T x 1,,1,1*⋯=。
取10=n 计算矩阵的条件数。
分别用顺序Gauss 消元、列主元Gauss 消元和完全选主元Gauss 消元方法求解,结果如何?(2)现选择程序中手动选取主元的功能,每步消去过程都选取模最小或按模尽可能小的元素作为主元进行消元,观察并记录计算结果,若每步消去过程总选取按模最大的元素作为主元,结果又如何?分析实验的结果。
(3)取矩阵阶数n=20或者更大,重复上述实验过程,观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异,说明主元素的选取在消去过程中的作用.(4)选取其他你感兴趣的问题或者随机生成的矩阵,计算其条件数,重复上述实验,观察记录并分析实验的结果。
1. 算法介绍首先,分析各种算法消去过程的计算公式, 顺序高斯消去法:第k 步消去中,设增广矩阵B 中的元素()0k kk a ≠(若等于零则可以判定系数矩阵为奇异矩阵,停止计算),则对k 行以下各行计算()(),1,2,,k ikik k kka l i k k n a ==++,分别用ik l -乘以增广矩阵B 的第k 行并加到第1,2,,k k n ++行,则可将增广矩阵B 中第k 列中()k kka 以下的元素消为零;重复此方法,从第1步进行到第n-1步,则可以得到最终的增广矩阵,即()()(),n n n B Ab ⎡⎤=⎣⎦; 列主元高斯消去法:第k 步消去中,在增广矩阵B 中的子方阵()()()()k kkkknk k nknn a a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦中,选取()k k i k a 使得()(k)max k k i k ik k i na a ≤≤=,当k i k ≠时,对B 中第k 行与第k i 行交换,然后按照和顺序消去法相同的步骤进行。

高等数值分析第三章作业参考答案1.考虑线性方程组Ax=b,其中A是对称正定矩阵.用Galerkin原理求解方程K=L=Span(v),这里v是一个固定的向量.e0=x∗−x0,e1=x∗−x1证明(e1,Ae1)=(e0,Ae0)−(r,v)2/(Av,v),(∗)其中r=b−Ax0.v应当取哪个向量在某种意义上是最佳的?证明.令x1=x0+αv,那么r1=r−αAv,e1=e0−αv.由Galerkin原理,有(r1,v)=0,因此α=(r,v)/(Av,v).注意到r1=Ae1,r=Ae,有(Ae1,v)=0.于是(e1,Ae1)=(e0−αv,Ae1)=(e0,Ae1)=(e0,Ae0)−α(e0,Av)=(e0,Ae0)−α(r,v)即(∗)式成立.由(∗)式知当v=e0时, e1 A=0最小,即近似解与精确解的误差在A范数意义下最小,算法一步收敛(但是实际中这个v不能精确找到);在最速下降意义下v=r时最佳.2.求证:考虑线性方程组Ax=b,其中A是对称正定矩阵.取K=L=Span(r,Ar).用Galerkin方法求解,其中r是上一步的残余向量.(a)用r和满足(r,Ap)=0的p向量构成K中的一组基.给出计算p的公式.解.设p=r+αAr,(r,Ap)=0等价于(Ar,p)=0.解得α=−(Ar,r)/(Ar,Ar).(b)写出从x0到x1的计算公式.解.设x1=x0+β1r+β2p,那么r1=r−β1Ar−β2Ap,再由Galerkin原理,有(r1,r)=(r1,p)=0,解得β1=(r,r)/(Ar,r),β2=(r,p)/(Ap,p).(c)该算法收敛吗?解.该算法可描述为:(1)选初始x0∈R n,计算初始残差r0=b−Ax0,ε>0为停机准则;(2)对k=0,1,2,...直到 r k <εαk=−(r k,Ar k) (Ar k,Ar k);p k=r k+αAr k;βk=(r k,r k) (Ar k,r k);γk=(r k,p k) (Ap k,p k);r k+1=r k−βk Ar k−γk Ap k;x k+1=x k+βk r k+γk p k.此算法本质上是由CG迭代一步就重启得到的,所以是收敛的,下面给出证法.设用此算法得到的x k+1=x k+¯p1(A)r k,那么e k+1 A=minp1∈P1e k+p1(A)r k A≤ e k+¯p1(A)r k A= e k−¯p1(A)Ae k A≤max1≤i≤n|˜p(λi)| e k A其中0<λ1≤...≤λn为A的特征值,˜p(t)=1−t¯p1(t)是过(0,1)点的二次多项式.当˜p满足˜p(λ1)=˜p(λn)=−˜p(λ1+λn2)时可使max1≤i≤n|˜p(λi)|达到最小.经计算可得min ˜p max1≤i≤n|˜p(λi)|≤(λ1−λn)2(λ1−λn)2+8λ1λn<1故若令κ=λ1/λn,则e k+1 A≤(κ−1)2κ2+6κ+1e k A,方法收敛.3.考虑方程组D1−F−E−D2x1x2=b1b2,其中D1,D2是m×m的非奇异矩阵.取L1=K1=Span{e1,e2,···,e m},L2= K2=Span{e m+1,e m+2,···,e n}.依次用(L1,K1),(L2,K2)按讲义46和47页公式Az∗=r0r0−Az m⊥LW T AV y m=W T r0x m=x0+V(W T AV)−1W T r0各进行一步计算.写出一个程序不断按这个方法计算下去,并验证算法收敛性.用L i=AK i重复上述各步骤.解.对任意给定x0=x(0)1x(0)2,令r=b−Ax0,V1=[e1,e2,...,e m],V2=[e m,e m+1,...,e n].对L i=K i情形,依次用(L1,K1),(L2,K2)各进行一步计算:(L1,K1)(L2,K2)z(1) 1=V1y1z(2)1=V2y2r0−Az(1)1⊥L1r0−Az(2)1⊥L2(V T1AV1)y1=V T1r0,D1y1=V T1r0(V T2AV2)y2=V T2r0,−D2y2=V T2r0x(1)1=x(1)+V1D−11V T1r0x(2)1=x(2)−V2D−12V T2r0得如下算法:(1)选初始x0∈R n,计算初始残差r0=b−Ax0,ε>0为停机准则;(2)对k=1,2,...直到 r k <ε求解D1y1=r k−1(1:m);求解−D2y2=r k−1(m+1:n);x k=x k−1+V1y1+V2y2;r k=r k−1−AV1y1−AV2y2.收敛性:r k=r k−1−AD−11−D−12rk−1=0−F D−12ED−11rk−1Br k−1算法收敛⇔ρ(B)<1⇔ρ(ED−11F D−12)<1.对L i=AK i情形,依次用(L1,K1),(L2,K2)各进行一步计算:(L1,K1)(L2,K2)z(1) 1=V1y1∈K1z(2)1=V2y2∈K2r0−Az(1)1⊥L1=AK1r0−Az(2)1⊥L2=AK2(V T1A T AV1)y1=V T1A T r0(V T2A T AV2)y2=V T2A T r0(D T1D1+E T E)y1=V T1A T r0(D T2D2+F T F)y2=V T2A T r0x(1) 1=x(1)+(D T1D1+E T E)−1V T1A T r0x(2)1=x(2)+(D T2D2+F T F)−1V T2A T r0得如下算法:(1)选初始x0∈R n,计算初始残差r0=b−Ax0,ε>0为停机准则;(2)对k=1,2,...直到 r k <ε求解(D T1D1+E T E)y1=(A T r k−1)(1:m);求解(D T2D2+F T F)y2=(A T r k−1)(m+1:n);x k=x k−1+V1y1+V2y2;r k=r k−1−AV1y1−AV2y2.收敛性:r k=r k−1−A(D T1D1+E T E)−1(D T2D2+F T F)−1A T rk−1(I−B)r k−1算法收敛⇔ρ(I−B)<1⇔0<λ(B)<2.4.令A=3−2−13−2...............−2−13,b=1...2用Galerkin原理求解Ax=b.取x0=0,V m=W m=(e1,e2,···,e m).对不同的m,观察 b−Ax m 和 x m−x∗ 的变化,其中x∗为方程的精确解.解.对于 b−Ax m 和 x m−x∗ ,都是前n−1步下降趋势微乎其微,到第n步突然收敛。

高等数值分析第二次实验作业Tl・构造例子特征值全部在右半平面时,观察基本的Arnold!方法和GMRES方法的数值性态,和相应重新启动算法的收敛性.Answer:(1)构造特征值均在右半平面的矩阵A:根据实Schur分解,构造对角矩阵D由n个块形成,每个对角块具有如下形式,对应一对特征值a - ± ip t£ 2 ⑴5,=lA e丿这样D=diag(Si,S2,S3……SJ矩阵的特征值均分布在右半平面。
生成矩阵A=U T AU,其中U为正交阵,则A矩阵的特征值也均在右半平面。
不妨构造A如下所示:1 -11 12 -22 2n/2 -〃/2n/2 n/2由于选择初值与右端项:xO=zeros(2*N, l);b=ones(2*N t l);则生成矩阵A的过程代码如下所示:N=500 %生成八为2N阶A=zeros(2*X);for a=l:NA(2*a-112*a-1)=a;A(2*a-L.2*a)=-a;A(2*a,2*a-l)=a;A(2*a,2*a) =a;endU = orth(rand(2*N.2*N));Al = IT 林*U;(2)观察基本的Arnoldi和GMRES方法编写基本的Arnold!函数与基本GMRES函数,具体代码见附录。
Function [x,rm,flag]=Arnoldi(A f b t xO,tol,m)function [x t rm,flag]=GMRES(A t b t xO,tol.m)输入:A为方程组系数矩阵,b为右端项,xO为初值,tol为停机准则,m为人为限制的最大步数。
输出:x为方程的解,nn为残差向虽,flag为解是否收敛的标志。
外程序如下所示: e=le-6; m=700; tic[xA,rmA t flagA]=Arnoldi (A 1, b, xO t e.m); toe tic[xG,rmG.flagG]=GMRES(Al,b,x0,e,m); toesubplot(1,2,1); semi logy(rmA)title(r /\rnoldiE O A 2 u I R ') xlabel (r p u z u 2 Vi E y k*) ylabelC log(| | rk |)') subplot(1,2,2); semi logy(rmG)title(r GMRESE 6 A 2 u I R ') xlabel (r p u z u 2 Vi E y k*) ylabelC log(| |rk| |)') 得到:waa迭代次数 546526运行时间(s)Arnold"攵敛曲线10?f --------------------- ■------------------- l101 :\10° : 102101•1-2 o1 1 (-¥--) 60-10200 400 迭代步数k 600 >方法ArnoldiGMRES10°=亘)60200 400 迭代步数k600GMRES 收敛曲线得到两种方法的收敛曲线如上所示,将计算结果整理在下表中:结果讨论:1.从图中可以看出,基本的Arnoldi方法经过546步收敛,基本的GMRES方法经过526步收敛,基本的GMRES收敛速度会略烘于基本的Arnoldi方法。


20130917题目求证:在矩阵的LU 分解中,111n n Tn ij i j j i j L I e e α-==+⎛⎫=- ⎪⎝⎭∑∑证明:在高斯消去过程中,假设0jj a ≠ ,若a=0,可以通过列变换使得前面的条件成立,这里不考虑这种情况。
对矩阵A 进行LU 分解,()()()()()1111111L M n M M M n ---=-=∙∙-………… ,其中()1n Tn ij i j i j M j I e e α=+⎛⎫=+ ⎪⎝⎭∑ ,i e 、j e 为n 维线性空间的自然基。
()M j 是通过对单位阵进行初等变换得到,通过逆向的变换则可以得到单位阵,由此很容易得到()M j 的逆矩阵为1n Tn ij i j i j I e e α=+⎛⎫- ⎪⎝⎭∑。
故111n n T n ij i j n j i j L I e e I α-==+⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭∏∑上式中的每一项均是初等变换,从右向左乘,则每乘一次相当于对右边的矩阵进行一次向下乘法叠加的初等变换。
由于最初的矩阵为单位阵,变换从右向左展开,因而每一次变换不改变已经更新的数据,既该变换是从右向左一列一列更新数据,故11nn Tn ij i j j i j L I e e α==+⎛⎫=- ⎪⎝⎭∑∑。
数学证明:1nTi j i ji j ee α=+⎛⎫ ⎪⎝⎭∑具有,000n j jA -⎛⎫ ⎪⎝⎭ 和1,1000n j n j B -+-+⎛⎫⎪⎝⎭ 的形式,且有+1,-11,10000=000n j j n j n j AB --+-+⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭ 而11n n T ij i j j k i j e e α-==+⎛⎫ ⎪⎝⎭∑∑具有1,1000n k n k B -+-+⎛⎫⎪⎝⎭的形式,因此:1311111211121==n n n n n n T T T n ij i j n ij i j n ik i k j i j j i j k n i k n n T n i i n ik i i i k L I e e I e e I e e I e e I e ααααα---==+==+=-=+==+⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=---⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫⎛⎫=-- ⎪ ⎪ ⎝⎭⎝⎝⎭∏∑∏∑∑∑∑∑……11211n n n T Tk n ik i kk k i k e I e e α--===+⎛⎫⎛⎫=- ⎪⎪ ⎪⎭⎝⎭⎝⎭∑∑∑#20130924题目一问:能否用逐次householder 相似变换变实矩阵A 为上三角矩阵,为什么?解:不能用逐次householder 相似变换变A 为上三角矩阵,原因如下:A 记作:()12=,,n A a a a ……, ,存在householder 阵1H s.t. 1111H a e α= ,则()()()111111111111111111111,,,0T Th H AH H a A H e H A H e H A H h H A H ααα⎛⎫'''=== ⎪⎪'⎝⎭⎛⎫''=+ ⎪ ⎪⎝⎭11H A H ''第一列的元素不能保证为1e 的倍数,故无法通过householder 变换实现上三角化。

非线性方程的解法实验1.算法设计与比较问题提出:非线性方程组的求解方法很多,基本的思想是线性化。
不同的方法效果如何,要靠计算的实践来分析、比较。
实验内容:考虑算法(1)牛顿法(2)拟牛顿法分别编写它们的matlab程序。
实验要求:(1)用上述方法,分别计算两个例子。
在达到精度相同的前提下,比较迭代次数、浮点运算次数和CPU时间等。
1.1程序清单为使用flops统计浮点运算次数,使用MATLAB5.3版本%f1.m原函数f1function y=f(x)y(1)=12*x(1)-x(2)^2-4*x(3)-7;y(2)=x(1)^2+10*x(2)-x(3)-8;y(3)=x(2)^3+10*x(3)-8;end%ff1.m原函数f1的雅克比矩阵function y=ff(x)y(1,:)=[12,-2*x(2),-4];y(2,:)=[2*x(1),10,-1];y(3,:)=[0,3*x(2)^2,10];end%f1.m原函数f2function y=f2(x)y(1)=3*x(1)-cos(x(2)*x(3)) -1/2;y(2)=x(1)^2-81*(x(2)+0.1)^2+sin(x(3))+1.06;y(3)=exp(-x(1)*x(2))+20*x(3)+1/3*(10*pi-3);end%ff2.m原函数f2的雅克比矩阵function y=ff2(x)y(1,:)=[3,x(3)*sin(x(2)*x(3)),x(2)*sin(x(2)*x(3))];y(2,:)=[2*x(1),-2*81*(x(2)+0.1),cos(x(3))];y(3,:)=[-x(2)*exp(-x(1)*x(2)),-x(1)*exp(-x(1)*x(2)),20]; end%牛顿法(以第一个方程组为例)clear;x0=[0,0,0]';n=10;tol=1e-6;x(:,1)=x0;i=1;u=[1,1,1]';tic;while (norm(u)>tol*norm(x(:,i))&(i<n))A=ff1(x(:,i));b=f1(x(:,i))';u=-A\b;x(:,i+1)=x(:,i)+u;i=i+1;end;x(:,i)iter=i-1t=toc%拟牛顿法(以第一个方程组为例)clear;x0=[0,0,0]';n=10;tol=1e-6;x(:,1)=x0;i=1;p=[1,1,1]';A=ff1(x(:,1));tic;while (norm(p)>tol*norm(x(:,i))&(i<n))x(:,i+1)=x(:,i)-A\f1(x(:,i))';p=x(:,i+1)-x(:,i);q=f1(x(:,i+1))'-f1(x(:,i))';A=A+(q-A*p)*p'/norm(p,2)^2;i=i+1;end;iter=i-1t=tocx(:,i)1.2运行结果1.2.1第一个方程组精确解为*T =(0.886020214719037, 0.796444775323146, 0.749479574122230)x 取最大迭代次数n=5000,相对误差限Tol=1e-6 (1)取()(0)1,1,1x T=牛顿迭代法迭代3次收敛,浮点运算次数为440,每次迭代平均浮点运算次数为147,CPU 耗时t =0(s)拟牛顿法迭代4次收敛,浮点运算次数为1048,每次迭代平均浮点运算次数为262,CPU 耗时t =0(s)(2)取()(0)000x T =,, 牛顿迭代法迭代4次收敛,浮点运算次数为510,每次迭代平均浮点运算次数为128,CPU 耗时t =1.600e-002(s)拟牛顿法迭代6次收敛,浮点运算次数为1493,每次迭代平均浮点运算次数为248,CPU 耗时t =1.50e-002(s)(3)取()(0)50,5050x T=,牛顿迭代法迭代15次收敛,浮点运算次数为2118,每次迭代平均浮点运算次数为141,CPU 耗时t =1.600e-002(s)拟牛顿法迭代338次收敛,浮点运算次数为88454,每次迭代平均浮点运算次数为262,CPU 耗时t =3.100e-002(s)1.2.2第二个方程组精确解为*T =(0.886020214719037, 0.796444775323146, 0.749479574122230)x 取最大迭代次数n=5000,相对误差限Tol=1e-6(1)取()(0)000x T=,, 牛顿迭代法迭代5次收敛,浮点运算次数为776,每次迭代平均浮点运算次数为155.2,CPU 耗时t =0(s)拟牛顿法迭代6次收敛,浮点运算次数为1635,每次迭代平均浮点运算次数为273,CPU 耗时t =0(s)(2)取()(0)888x T=,, 牛顿迭代法迭代9次收敛,浮点运算次数为1519,每次迭代平均浮点运算次数为169,CPU 耗时t =0(s)拟牛顿法迭代21次收敛,浮点运算次数为5924,每次迭代平均浮点运算次数为282,CPU 耗时t =1.600e-002(s)(3)对于离精确解更远的初值(如()(0)101010x T=,,),在计算中会出现奇异或接近奇异的矩阵,计算结果误差很大或计算根本无法进行下去。
数值分析上机实验学生姓名: 学号: 教师:实验1:1. 实验项目的性质和任务通过上机实验,使学生对病态问题、线性方程组求解和函数的数值逼近方法有一个初步理解。
2.教学内容和要求 1)对高阶多多项式201()(1)(2)(20)()k p x x x x x k ==---=-∏编程求下面方程的解 19()0p x x ε+=并绘图演示方程的解与扰动量ε的关系。
Matlab 程序:x=1:20;y=zeros(1,20); ve=zeros(1,21); plot(x,y,'o') hold on ; pause; for x=1:5ve(2)=10^(-x);e=roots(poly(1:20)+ve);plot(e,'*') hold on pause; end0510152025303540-20-15-10-5051015202)对2~20n =,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组 n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
Matlab 程序:for n=2:20; H=hilb(n); ca=cond(H,2) x=(1:n)'; b=H*x; [L,U]=lu(H); y=L\b;x1=U\yplot(x,x,'o',x1,x1,'*') hold on pause; end-500-400-300-200-100100200300400500-500-400-300-200-10001002003004005003)对函数 21()[1,1]125f x x x=∈-+的Chebyshev 点 (21)cos()1,2,...,12(1)kk x k n n π-==++编程进行Lagrange 插值,并分析插值结果。
Matlab 程序:function y=lagrangen(x0,y0,x) n=length(x0);m=length(x); for i=1:m z=x(i);s=0;for k=1:nL=1;for j=1:nif j~=kL=L*(z-x0(j))/(x0(k)-x0(j));endends=s+L*y0(k);endy(i)=s;endy;for n=5:20x=-1:0.01:1; y=1./(1+25*x.^2);plot(x,y,'r')hold onk=n+1:-1:1;x0=cos((2*k-1)*pi./(2*(n+1))),y0=1./(1+25*x0.^2);x=-1:0.01:1; y1=lagrangen(x0,y0,x);plot(x0,y0,'o',x,y1), pausehold off end-1-0.8-0.6-0.4-0.200.20.40.60.81-0.200.20.40.60.811.2-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81。
1. 解:由于求解Ax b =等价于极小化2Ax b -,相当于极小化泛函:()()1,2x Ax b Ax b ϕ=-- 从任一k x 出发,沿着()x ϕ在k x 点下降最快的方向搜索下一个近似点1k x +,使得()1k x ϕ+在该方向上达到极小值,最速下降方向为:()()T T k k x A Ax b A r ϕ-∇=--=令1,T k k k k k k p A r x x p α+==+,需要寻找合适的k α使得()()11min k k Rx x αϕϕ++∈=,则()()()()()()1,=T T T T k k k k k k k k d x x p p A A x p b p A p r d ϕϕααα+=∇=+-- 令()0d x d ϕα=,可得: ()()()(),,,,k k k k k k k k k Ap r p p Ap Ap Ap Ap α==则()22,0k k d Ap Ap d ϕα=>,因此上式的k α即为所求 于是得到极小化泛函()()1,2x Ax b Ax b ϕ=--的最速下降法: 1) 选取初值0n x R ∈,计算00r b Ax =-2) k=0,1,2,……若k r ε≤,则停止;ε为事先给定的停机场数;否则,k=k+1()()11;,;,;;T k k k k k k k k k k k k k k k p A r p p Ap Ap x x p r r Ap ααα++===+=-2. 解:()()111k k k k AAAx x x r x p A x x α***----=+-=-其中()1p A A α=-,设A 的特征根为120n λλλ≥≥≥> ,则有()11max k i k AAi nx x p x x λ**-≤≤-≤-当120αλ<<时,()1max 1i i np λ≤≤<,因此此方法收敛当()111n αλαλ-=--即12n αλλ=+时,()1max i i n p λ≤≤取最小值11n nλλλλ-+,此时收敛最快3. 解:设x *为方程组Ax b =精确解,k k e x x *=-,则()1,TT Tk k k E e e -=,则原迭代法等价于()110k k I A I E E I βαβ+⎡++-⎤=⎢⎥⎣⎦令()10I A I B I βαβ⎡++-⎤=⎢⎥⎣⎦,则迭代法收敛等价于()1B ρ<,即()1,1i B i nλ<≤≤,令0B I λ-=,即 ()10n I A ββλαλλ⎛⎫+--+-= ⎪⎝⎭ 当0λ≠时,则有10I A ββλαλ⎛⎫+--+= ⎪⎝⎭设120n μμμ≥≥≥> 是A 的特征根,则有()210101112i i i ββλαμλλβαμλβλβαμβ+--+=-+++=<⇔++<+<则有:()()()11112,1211,0,1211,0i i B i ni n ρβαμβββαμββαμ<⇔++<+<≤≤+⇔<-<<≤≤+⇔<-<< 4.5. 证明:反证法。
第1章绪论内容提要#〜误差度量1数值分析研究两类误差:舍入误差和截断误差,由于计算机字长的有限性,对相关数据进行存储表示时便产生舍入误差,计算机必须在有限的时间内得到运行结果,于是无穷的运算过程必须截断为有限过程,由此产生截断误差,2,误差的度量分式有:绝对误差(限)、相对误差(限〗和有效数字,设?是真值工的一个近似,绝对误差为一:!相对误差为& ,绝对误差限〉和相对误X X差限6^ 〉分别是〉 |和^(:^ ^|的上限,3^对于非零近似值^的如下规格化标准形式X^ ^ 10^ X0#!1X2'&X&,&!' ?X I ^0 〈1. 1〉如果存在尽可能大的&,使得〉| & ^乂10"-",则称?有"位有效数字.进而当&^》时,称X,是有效数.4,有效数字和相对误差的关系定理1. 1 如果形如式〈1. V的有&位有效数字,则定理1.2如果形如式〈1. 0的:^的相对误差满足^|《"二" X化1-"则纟^至少有&位有效数字,二、浮点数系统对于5+ ^ + 2位的浮点数系0表示二进制阶码数值的二进制位数〃表示尾数的二进制位数,其他两位表示阶码和尾数的符号〉,机器数绝对值的范围是2-21〜22'-、实数表示的相对舍入误差限是2-'.当数据的绝对值大于22'-1时,计算机非正常停机,称之为上溢,当非零数据的绝对值小于2-2',用机器零表示,精度损失,称之为下溢,、误差传播如果在运算过程中舍入误差能够得到控制,或者舍入误差的增长不影响产生可靠的结果则纟称该算法是数值稳定的,函数值绝对误差传播公式如下^/(^" 丫) ## /(;:)〉 1 2〉^(/(^" ^-^:》#亡"";二…、^ 〉(丄门)!.^^")〉#| /'(?) |〈1.4〉、数值稳定性不同的教材对数值方法稳定性的定义有所不同,有的要求随计算过程的深入误差不增长,有的则要求误差增长速度不能太快^只要不影响产生具有有效数字的近似值即认为是稳定的,读者应注意教材中的定义.随着学习的深入,会针对各种具体算法给出稳定性的确切定义,^ 2 ^典型例题与解题技巧【例1】求!&的近似值,使其绝对误差限精确到1乂1。
第1部分方法介绍奇异值分解(SVD )定理:设m n A R ⨯∈,则存在正交矩阵m m V R ⨯∈和n n U R ⨯∈,使得TO A V U O O ∑⎡⎤=⎢⎥⎣⎦其中12(,,,)r diag σσσ∑= ,而且120r σσσ≥≥≥> ,(1,2,,)i i r σ= 称为A 的奇异值,V 的第i 列称为A 的左奇异向量,U 的第i 列称为A 的右奇异向量。
注:不失一般性,可以假设m n ≥,(对于m n <的情况,可以先对A 转置,然后进行SVD 分解,最后对所得的SVD 分解式进行转置,就可以得到原来的SVD 分解式)方法1:传统的SVD 算法主要思想:设()m n A R m n ⨯∈≥,先将A 二对角化,即构造正交矩阵1U 和1V 使得110T B n U AV m n⎡⎤=⎢⎥-⎣⎦其中1200n n B δγγδ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦然后,对三角矩阵T T B B =进行带Wilkinson 位移的对称QR 迭代得到:T B P BQ =。
当某个0i γ=时,B 具有形状12B O B O B ⎡⎤=⎢⎥⎣⎦,此时可以将B 的奇异值问题分解为两个低阶二对角阵的奇异值分解问题;而当某个0i δ=时,可以适当选取'Given s 变换,使得第i 行元素全为零的二对角阵,因此,此时也可以将B 约化为两个低阶二对角阵的奇异值分解问题。
在实际计算时,当i B δε∞≤或者()1j j j γεδδ-≤+(这里ε是一个略大于机器精度的正数)时,就将i δ或者i γ视作零,就可以将B 分解为两个低阶二对角阵的奇异值分解问题。
主要步骤:(1)输入()m n A R m n ⨯∈≥及允许误差ε(2)计算Householder 变换1,,,n P P ⋅⋅⋅,12,,n H H -⋅⋅⋅,使得112()()0Tn n B nP P A H H m n -⎡⎤⋅⋅⋅⋅⋅⋅=⎢⎥-⎣⎦其中1200n n B δγγδ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 12:n U PP P =⋅⋅⋅,122:.n V H H H -=⋅⋅⋅ (3)收敛性检验:(i )将所有满足()1j j j γεδδ-≤+的j γ置零;(ii )如果0,2,,j j n γ== ,则输出有关信息结束;否则,1:0γ=,确定正整数p q <,使得10p q n γγγ+==⋅⋅⋅==,0j γ≠,p j q <≤;(iii )如果存在i 满足1p i q ≤≤-使得i B δε∞≤,则:0i δ=,1:i x γ+=,1:i y δ+=,1:0i γ+=,:1l =,转步(iv );否则转步(4) (iv )确定cos ,sin c s θθ==和σ使0c s x s c y σ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦这也相应于0Tc s y s c x σ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦所以可以直接调用'Given s 变换算法得到:i l δσ+=,:(,,)T U UG i i l θ=+这相当于(1:;,)(1:;,)(1:;,)Tc s c s U n i i l U n i i l U n i i l s c s c -⎡⎤⎡⎤+=+=+⎢⎥⎢⎥-⎣⎦⎣⎦(v )如果l q i <-,则1:i l x s γ++=,11:i l i l c γγ++++=,1:i l y δ++=,:1l l =+转步(iv ),否则转步(i )(4)构造正交阵P 和Q ,使12=T P B Q B 仍为上双对角阵,其中112100pp p p q q B δγδγγδ+++⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦, 得121:=T B B P B Q =,:(,,)p n p q U Udiag I P I --=,:(,,)p n p q V Vdiag I Q I --=然后转步(3)。
高等数值分析实验一
工物研13 成彬彬2004310559
一.用CG,Lanczos和MINRES方法求解大型稀疏对称正定矩阵Ax=b
作实验中,A是利用A= sprandsym(S,[],rc,3)随机生成的一个对称正定阵,S是1043阶的一个稀疏阵
A= sprandsym(S,[],0.01,3);
检验所生成的矩阵A的特征如下:
rank(A-A')=0 %即A=A’,A是对称的;
rank(A)=1043 %A满秩
cond(A)= 28.5908 %A是一个“好”阵
1.CG方法
利用CG方法解上面的线性方程组
[x,flag,relres,iter,resvec] = pcg(A,b,1e-6,1043);
结果如下:
Iter=35,表示在35步时已经收敛到接近真实x
relres= norm(b-A*x)/norm(b)= 5.8907e-007为最终相对残差
绘出A的特征值分布图和收敛曲线:
S=svd(A); %绘制特征值分布
subplot(211)
plot(S);
title('Distribution of A''s singular values');;
xlabel('n')
ylabel('singular values')
subplot(212); %绘制收敛曲线
semilogy(0:iter,resvec/norm(b),'-o');
title('Convergence curve');
xlabel('iteration number');
ylabel('relative residual');
得到如下图象:
为了观察CG方法的收敛速度和A的特征值分布的关系,需要改变A的特征值:
(1).研究A的最大最小特征值的变化对收敛速度的影响
在A的构造过程中,通过改变A= sprandsym(S,[],rc,3)中的参数rc(1/rc为A的条件数),可以达到改变A的特征值分布的目的:
通过改变rc=0.1,0.0001得到如下两幅图
以上三种情况下,由收敛定理2.2.2计算得到的至多叠代次数分别为:48,14和486,由于上实验结果可以看出实际叠代次数都比上限值要小较多。
由以上三图比较可以看出,A的条件数越大,即A的最大最小特征值的差别越大,叠代所需要的步骤就越多,收敛越慢。
(2)研究A的中间特征值的分布对于收敛特性的影响:
为了研究A的中间特征值的分布对收敛速度的影响,进行了如下实验:
固定A的条件数,即给定A的最大最小特征值,改变中间特征值得分布,再来生成A,具体的实现方法是,先将原来的生成A进行特征值分解:
[U,S]=svd(A);
靠近最小特征值,得到对角阵C1。
再通过如下命令得到经处理后的矩阵A3:
A3=U*C1*U’;
对A3重新利用CG方法求解线性方程组得到如下结果图:
当他们都更靠近最小特征值时,结果如下:
靠近最大特征值,得到对角阵C2。
再通过如下命令得到经处理后的矩阵A4:
A4=U*C2*U’;
对A4重新利用CG方法求解线性方程组得到如下结果图:
当他们都更靠近最大特征值时,结果如下:
从以上实验基本可以得出以下结论,A的中间特征的分布对收敛速度的影响是很大的,其影响规律可以总结为:当中间特征值越靠近两头时,也就是说集中到一端时,收敛速度越快,当中间特征值的分布越对称时,收敛速度越慢,这里只能给出实验结果,还没能从数学理论上证明结论的正确性,尚待商讨。
2.Lanczos方法
自己编制Lanczos方法的程序如下:
clear
load A%A is the same as in the CG Method
b=ones(length(A),1);
bn=norm(b);
q(:,1)=zeros(length(b),1);q(:,2)=b/bn;
r(:,1)=b;bata=1;
for k=(1:length(b)) %Realize k-step Lanczos process
r(:,k+1)=A*q(:,k+1)-bata*q(:,k);
alfa=q(:,k+1)'*r(:,k+1);
r(:,k+1)=r(:,k+1)-alfa*q(:,k+1);
rm=norm(r(:,k+1));
if(rm>1e-6)
bata=rm;
q(:,k+2)=r(:,k+1)/bata;
end
e(k)=norm(eye(k)-q(:,2:k+1)'*q(:,2:k+1));
T=q(:,2:k+1)'*A*q(:,2:k+1); %Construct Tk
T1=svd(T);
if (T1(k)>1e-12) %T is not singular
t=inv(T);
rn(k)=t(k,1)*bata; %The relative residual is lie on the
if abs(rn(k))<3e-6 %Last element of inv(T)'s first column
yk=t(:,1)*bn; %Once reach the required precision,stop
break %and calculate yk,then x.
end
end
end
x=q(:,2:k+1)*yk;
semilogy(e);
程序运行及调试情况:一开始将残量rn定义在1e-6时认为收敛,结果发现程序收敛不了,单步运行时发现执行到k=33时残量就开始一直增大,跟踪Tk发现这时它已经和三对角阵误差很大,例如有些本来应改为0的元素已经达到1e-6的量级,再要求最终结果精度在1e-6就不现实了。
如果强制将Tk转化为三对角(即,把该为0的地方清0),则不会出现这种情况,结果收敛。
也就是说该程序达不到任意期望的精度。
不过运行时发现程序执行的时间比直接用inv(A)*b命令的执行时间还是要短的,虽然不知道此命令使用什么方法解的,但是说明Lanczos方法的执行效率还是很高。
解得如下结果(收敛曲线):可看出曲线后面参量已经开始上跳。
3.MINRES方法:
程序如下:
[x,flag,relres,iter,resvec] = minres(A,b,1e-6,1043);
semilogy(0:iter,resvec/norm(b),'-o');
title('Convergence curve');
xlabel('iteration number');
ylabel('relative residual');
绘得的收敛曲线如下:
二.当b是由A的部分特征向量生成时,三种方法的收敛情况:[U S]=svd(A); %对A进行特征值分解
n=10;
C=rand(n,1); %随机生成向量C
b=U(:,1:n)*C; %构造b由A的前n个特征相量生成
(1).CG的结果如下:三幅图分别对应n=10,100,1000的情况
(2)Lanczos的结果为:
以下三幅图分别对应n=10,100,1000的收敛曲线
下面的四幅图是念0,100,1000和原来的一般情况下norm(I-Q(k)’*Q(k)随k的增长情况,由图中可以看出,当n较大和在原来的情况下,Q(k)已经和一个正交阵相差较远,即k 较大时,它的各列已不能看成是正交的。
(3).MINRES方法的结果为:
结论:
由各种方法的结果均可以看出,当b由A的n个特征相量生成时,CG收敛性明显较好,并且n越小越好,当n接近A的阶数时,叠代次数趋向于一般情况.
三.利用三种方法解对称不定A的线性方程组,给出收敛曲线。
还是利用上述的1043阶的矩阵A,对它进行特征值分解后,修改它的特征值为有正有负后,再构造新的A。
[U,S]=svd(A); %对A特征值分解
g=10; %通过g可以改变负特征值的位置
for(i=1:5) %同过igai变特征值的个数
S(g+i,g+i)=-S(g+i,g+i);
end
A=U*S*U'; %重新构建A
(1). CG运行结果:
b=ones(length(A),1)时,
方法很快中断,不能够得到方程的解,如下图所示:
当b由A的10个特征相量构成时,方法能够得到方程的解:如下图
用CG方法解对称不定方程时,可能发生中断,而得不到方程的解。
所以CG方法对于对称不定方程不能普遍适用。
(2). Lanczos方法:
用Lanczos方法解对称不定方程,残量会产生振荡收敛的情况,振荡点代表Tk接近奇异,图中有5个振荡峰,这是由于A有5个负的特征值造成的,这说明Lanczos方法在解对称不定方程时不时最优的,没有使残量单调下降.
(3).MINRES方法
可以看出,解对称不定方程的MINRES方法的残量是单调下降的。
下面构造A只有5个不同的特征值,其中有2个是负的,以验证结论:当A只有k个不同的特征值时,MINRES方法至多k步找到准确解:。