清华大学高等数值计算(李津)实践题目二(SVD计算及图像压缩)(包含matlab代码)
- 格式:docx
- 大小:4.29 MB
- 文档页数:21

Technology Research of Image Compression Based on S V D陈一虎 Chen Yih u(宝鸡文理学院,宝鸡 721013)(Baoji Un i versity of Arts and Sciences ,Baoji 721013,Chin a )摘 要 : 数字图像处理方法的研究源于两个主要领域:一是便于人们分解图像,对图像信息进行改进;二是使机器能自动理解图像。
后者正是我们所要研究的内容。
众所周知,在计算机中,图像是通过矩阵来表示的,一幅图像对应着一个矩阵,对图像的压缩就转换成了对矩阵的处理。
在数学中,对矩阵进行奇异值分解可以把一个矩阵分解成只用几个数来表示,而且这种分解具有很好的稳定性、唯一性和自相似性。
通过这种方法,就能用比较少的数据来表示相应的图像。
本文就是通过对图像的矩阵进行奇异值分解,将一幅图像转换成只包含几个非零值的奇异值矩阵, 实现图像压缩。
Abstr ac t : The theory about DIP (D i g i ta l Image Processing) i s used in two fi l e d. One i s the i m provement of the i nforma ti on about i ma g e , and theother i s the saving, transport and display. And the l a tter i s the object that we researched. It i s we ll known that the graph i s presented by matri x i ncomputer. So we can de a l w ith a graph by using the matrix. In m ath by using the mu l ti resolu ti on SVD, the matrix can be decomposed into just a fewnumbers, and the decompos i ti on i s very stable, un i qu e , and se l f -s i mi l a r. By this method ,we can express di g i ta l i ma g e w itn l e ss data. This paper propos es amu l ti resolu ti on form of the sin g u l a r va l u e decompos i ti o n (SVD), and shows how it may be used for si g n a l a n a l ysi s and a pprox ima ti on. D i g i ta l i ma g e i stransformed into s in g u l a r va l u e matrix that conta i n s nonzero sin g u l a r va l u e s by s in g u l a r va l u e decompos i ti on (SVD) so that the i ma ge i s compre sse d.关 键 词 : 图像压缩;矩阵;奇异值分解Key w o r d s : i ma g e depre ss ;ma tr i x ;s in g u l a r va l u e decompos i ti on文 章 编 号 :1006-4311(2011)13-0169-02中 图 分 类 号 :TP319 文 献 标 识 码 :A 存储和传输问题。


20130917题目求证:在矩阵的LU 分解中,111n n Tn ij i j j i j L I e e α-==+⎛⎫=- ⎪⎝⎭∑∑证明:在高斯消去过程中,假设0jj a ≠ ,若a=0,可以通过列变换使得前面的条件成立,这里不考虑这种情况。
对矩阵A 进行LU 分解,()()()()()1111111L M n M M M n ---=-=••-………… ,其中()1n Tn ij i j i j M j I e e α=+⎛⎫=+ ⎪⎝⎭∑ ,i e 、j e 为n 维线性空间的自然基。
()M j 是通过对单位阵进行初等变换得到,通过逆向的变换则可以得到单位阵,由此很容易得到()M j 的逆矩阵为1n T n ij i j i j I e e α=+⎛⎫- ⎪⎝⎭∑。
故111n n T n ij i j n j i j L I e e I α-==+⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭∏∑上式中的每一项均是初等变换,从右向左乘,则每乘一次相当于对右边的矩阵进行一次向下乘法叠加的初等变换。
由于最初的矩阵为单位阵,变换从右向左展开,因而每一次变换不改变已经更新的数据,既该变换是从右向左一列一列更新数据,故11nn Tn ij i j j i j L I e e α==+⎛⎫=- ⎪⎝⎭∑∑。
数学证明:1n Tij i j i j e e α=+⎛⎫ ⎪⎝⎭∑具有,000n j j A -⎛⎫ ⎪⎝⎭ 和1,1000n j n j B -+-+⎛⎫⎪⎝⎭ 的形式,且有+1,-11,10000=000n j j n j n j A B --+-+⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭而11n n T ij i j j k i j e e α-==+⎛⎫ ⎪⎝⎭∑∑具有1,1000n k n k B -+-+⎛⎫⎪⎝⎭的形式,因此: 1311111211121==n n n n n n T T T n ij i j n ij i j n ik i k j i j j i j k n i k n n T n i i n ik i i i k L I e e I e e I e e I e e I e ααααα---==+==+=-=+==+⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=---⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫⎛⎫=-- ⎪ ⎪ ⎝⎭⎝⎝⎭∏∑∏∑∑∑∑∑……11211n n n T Tk n ik i kk k i k e I e e α--===+⎛⎫⎛⎫=- ⎪⎪ ⎪⎭⎝⎭⎝⎭∑∑∑#20130924题目一问:能否用逐次householder 相似变换变实矩阵A 为上三角矩阵,为什么?解:不能用逐次householder 相似变换变A 为上三角矩阵,原因如下:A 记作:()12=,,n A a a a ……, ,存在householder 阵1H s.t. 1111H a e α= ,则()()()111111111111111111111,,,0T Th H AH H a A H e H A H e H A H h H A H ααα⎛⎫'''=== ⎪⎪'⎝⎭⎛⎫''=+ ⎪ ⎪⎝⎭11H A H ''第一列的元素不能保证为1e 的倍数,故无法通过householder 变换实现上三角化。
清华大学高等数值分析课程作业第二次实验 作业第一题:构造例子特征值全部在右半平面时,观察基本的Arnoldi 方法和GMRES 方法的数值性态,和相应重新启动算法的收敛性。
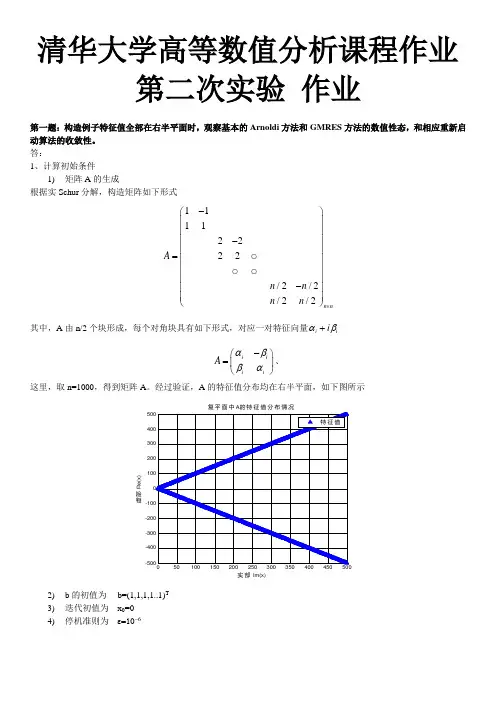
答:1、计算初始条件1) 矩阵A 的生成根据实Schur 分解,构造矩阵如下形式11112222/2/2/2/2n nA n n n n ⨯-⎛⎫ ⎪ ⎪ ⎪- ⎪= ⎪ ⎪ ⎪- ⎪⎪⎝⎭其中,A 由n/2个块形成,每个对角块具有如下形式,对应一对特征向量i i i αβ+ii i i A αββα-⎛⎫= ⎪⎝⎭、 这里,取n=1000,得到矩阵A 。
经过验证,A 的特征值分布均在右半平面,如下图所示50100150200250300350400450500-500-400-300-200-1000100200300400500复平面中A 的特征值分布情况实部 Im(x)虚部 R e (x )特征值2) b 的初值为 b=(1,1,1,1..1)T 3) 迭代初值为 x 0=0 4) 停机准则为 ε=10-62、基本的Arnoldi 和GMRES 方法代入前面提到的初始值A 、b 、x0,得到的收敛结果如下10020030040050060010-710-610-510-410-310-210-110两种基本算法的||r k ||收敛曲线 (阶数n=1000)迭代次数||r k ||/||b ||基本的Arnoldi 算法基本的GMRES 算法结果讨论:从图中可以看出,基本的Arnoldi 方法经过554步收敛,基本的GMRES 方法经过535步收敛。
这是由于GMRES 具有残差最优性,会略快于Arnoldi 方法,但是,由于两种方法的基本原理近似,GMRES 方法不会实质性的提速。
此外,从收敛曲线上看,由于特征值均处在右半平面,收敛曲线平滑,收敛速度(收敛因子)比较均匀。
3、重启动的GMRES 和Arnoldi 算法对上述A 、b 、x0使用重启动的Arnoldi 和GMRES 算法。

2024年考研高等数学二计算机视觉中的数学方法历年真题2024年的考研即将到来,高等数学作为计算机视觉的重要基础知识之一,在考试中占据着重要的分值。
为了帮助考生更好地应对考试,本文将通过回顾历年的真题,总结出计算机视觉中常见的数学方法,以期能为考生提供有益的参考和指导。
【前言】计算机视觉作为一门跨学科的研究领域,依赖于数学方法来实现图像的获取、处理和分析,其中高等数学是数学方法中的重要组成部分。
因此,在考研的高等数学二科目中,计算机视觉的题目涉及到的数学方法必不可少。
下面我们将具体看看历年真题中涉及到的数学方法。
【第一章:图像处理】1. 图像灰度化历年真题中,涉及到图像的处理过程,其中最常见的就是图像灰度化。
图像灰度化是将彩色图像转化为灰度图像,常用的转化方法有分量法、平均法和加权法等。
考生需要掌握这些方法,并能灵活运用于实际题目中。
2. 图像平滑和锐化为了去除图像中的噪声和增强图像的边缘特征,常常需要进行图像平滑和锐化操作。
图像平滑常用的方法有均值滤波和高斯滤波等,而图像锐化则可以通过拉普拉斯算子和梯度算子来实现。
对于考生来说,熟练掌握这些方法的原理和实现过程是十分重要的。
【第二章:模式识别】1. 特征提取模式识别中,特征提取是一个重要的环节。
特征提取的目的是从图像中提取出能够表征目标物体的特征信息,常用的特征包括边缘、角点、纹理等。
考生在备考过程中,需要熟悉各种特征提取方法,并且能够根据不同的应用场景选择合适的方法。
2. 分类器设计在模式识别中,分类器的设计是非常关键的一步。
常见的分类器包括最近邻分类器、支持向量机、决策树等。
考生需要了解各种分类器的原理和特点,并且能够根据具体的需求选择合适的分类器进行设计。
【第三章:图像分割】1. 阈值分割图像分割是指将图像分成若干个子区域,每个子区域内的像素具有一定的相似性。
在图像分割中,阈值分割是最基本且常用的方法之一。
通过设置合适的阈值,将图像中不同像素值的像素分割开来。

高等数值计算实践题目一1. 实践目的本次计算实践主要是在掌握共轭梯度法,Lanczos 算法与MINRES 算法的基础上,进一步探讨这3种算法的数值性质,主要研究特征值特征向量对算法收敛性的影响。
2. 实践过程(一)生成矩阵(1)作5个100阶对角阵i D 如下:1D 对角元:1,1,...,20,1+0.1(-20),21,...,100j j d j d j j ====2D 对角元:1,1,...,20,1+(-20),21,...,100j j d j d j j ==== 3D 对角元:,1,...,80,81,81,...,100j j d j j d j ====4D 对角元:,1,...,40,41,41,...,60,41+(60),61,...,100j j j d j j d j d j j =====-= 5D 对角元:,1,...,100j d j j ==记i D 的最大模特征值和最小模特征值分别为1iλ和in λ,则i D 特征值分布有如下特点:1D 的特征值有较多接近于i n λ,并且1/i i n λλ较小,2D 的特征值有较多接近于i n λ,并且1/i i n λλ较大, 3D 的特征值有较多接近于1i λ,并且1/i i n λλ较大,4D 的特征值有较多接近于中间模特征值,并且1/i i n λλ较大, 5D 的特征值均匀分布,并且1/i i n λλ较大(2)随机生成10个100阶矩阵j M :(100(100))j M fix rand =g并作它们的QR 分解,得j Q 和j R ,这样可得50个对称的矩阵Tij j i j A Q DQ =,其中i D 的对角元就是ij A 的特征值,若它们都大于0,则ij A 正定,j Q 的列就是相应的特征向量。
结合(1)可知,ij A 都是对称正定阵。
(二)计算结果以下计算,均选定精确解(100,1)exact x ones =,初值0(100,1)x zeros =由ij exact kA x b =计算得到k b (算法中要求解的精度为10e -)。

matlab数字图像处理图像运算+答案实验⼆:图像运算⼀、实验⽬的掌握MATLAB语⾔中图像数据的读取、显⽰与保存⽅法;掌握统计图像灰度直⽅图的⽅法理解直⽅图均衡的原理和作⽤,掌握图像直⽅图均衡化的⽅法理解图像点运算、代数运算、⼏何运算的基本定义和常见⽅法进⼀步熟悉了解MATLAB语⾔的应⽤⼆、知识要点1.数据类型及图像类型间的基本转换函数数据类转换:B = data_class_name(A);2.imhist(H);%显⽰a的直⽅图histeq(H); %将图像a进⾏直⽅图均衡化adapthisteq(H); %将图像a进⾏直⽅图均衡化3.图像的点运算点运算是通过对图像中每个像素值进⾏计算,改善图像显⽰效果的操作,也称对⽐度增强或对⽐度拉伸或灰度变换。
可以表⽰为B(x,y)=f(A(x,y)).进⾏逐点运算,输⼊映射为输出,不改变图像像素的空间关系。
Y=aX+b %线性点运算Y=X+aX(max(X)-X) %⾮线性点运算4.代数运算代数运算是指对两幅输⼊图像进⾏点对点的加、减、乘或除运算⽽得到输出图像的运算。
四种图像代数运算的数学表达式如下:C(i,j)=A(i,j)+B(i,j) C=imadd(A,B)C(i,j)=A(i,j)-B(i,j) C=imsubtract(A,B);C(i,j)=A(i,j)*B(i,j) C=immultiply(A,B)C(i,j)=A(i,j)/B(i,j) C=imdivide(A,B)5.图像加噪函数imnoise(参阅matlab help)imnoise的语法格式为J = imnoise(I,type)J = imnoise(I,type,parameters)其中J=imnoise(I,type)返回对原始图像I添加典型噪声的有噪图像J。
参数type 和parameters⽤于确定噪声的类型和相应的参数。
J = imnoise(I,'gaussian',m,v) %加⼊均值m,⽅差为v的⾼斯噪声,m默认值0,v默认值0.01J = imnoise(I,'poisson') %加⼊泊松分布的噪声J = imnoise(I,'salt & pepper',d)%加⼊密度为d的椒盐噪声,d的默认值为0.05 J = imnoise(I,'speckle',v) %加⼊均值0,⽅差为v的乘性噪声三、实验内容1、将给定的Couple.bmp图像⽂件读出并显⽰,显⽰其灰度直⽅图,分别⽤histeq、adapthiateq函数将其直⽅图均衡化,观察均衡后的图像及其直⽅图。

n a n b 5 x 2+ 3x 3 x 2+ 5x(n →∞ n - ⎪l n n nn →∞清华大学2019-2020学年第一学期《高等数学》本科测试题考试课程一元微积分(B )2020 年 10 月 25 日系名 班级姓名学号一.填空题(每空 3 分,共 15 题)(请将答案直接填写在横线上!)e tan x - e sin x1.lim x →0x - sin x= 。
2. lim sin πn →∞n 2 + n )=。
⎛ + ⎫n3. limn →∞⎝ ⎪= 。
2 ⎭n4.lim ⎛ n + ln n ⎫ln n = 。
⎝ ⎭5.当 x → 0 时, f( x ) =-x 的阶为 。
3 5 17 1 + 22n -16.已知 x n = • • • ...• 2 4 16 22 n -1 ,则lim x = 。
n →∞7. 设 x =(1+ a )(1+ a 2 )...(1+ a 2n),其中 a < 1,则lim x=。
8. 已知有整数n (n > 4)使极限 lim ⎡(x n + 7x 4+ 2)α - x ⎤ = A ≠ 0,则α=。
9.⎛ 23 -1 33 -1 43 -1 x →+∞ ⎢⎣⎥⎦ n 3 -1 ⎫ =。
lim 3 3 3... 3 ⎪ n →∞ ⎝2 +13 +14 +1 n +1 ⎭n10.lim ∑n →∞ k =1k 3 + 6k 2 +11k + 5 (k + 3)!= 。
⎛ 11. lim n →∞ ⎝ n 12 3 +12 + 22 n 3 + 22 + ...+ n 2 n 3 + n 2 ⎫ ⎪= 。
⎭ 12. lim 1!+ 2!+ ... + n != 。
n nn n!1+ x 2 2 )(α- β β 7 - 7 + 7 , 7 - 7 + 7 - 7 ,...k =113. 1 x 2+ 1- lim 2 = 。
x →0cos x - e x sin x 2n α=14. 已知limn →∞ n β- (n - 1)β =2017 ,则 。

第一章引言一.填空题1. 数字图像是用一个数字阵列来表示的图像。
数字阵列中的每个数字,表示数字图像的一个最小单位,称为像素2.像增强等;二是从图像到非图像的一种表示,如图像测量等。
5. 数字图像处理包含很多方面的研究内容。
其中,图像重建的目的是根据二维平面图像数据构造出三维物体的图像。
二.简答题1. 数字图像处理的主要研究内容包含很多方面,请列出并简述其中的4种。
①图像数字化:将一幅图像以数字的形式表示。
主要包括采样和量化两个过程。
②图像增强:将一幅图像中的有用信息进行增强,同时对其无用信息进行抑制,提高图像的可观察性。
③图像的几何变换:改变图像的大小或形状。
④图像变换:通过数学映射的方法,将空域的图像信息转换到频域、时频域等空间上进行分析。
如傅利叶变换等。
⑤图像识别与理解:通过对图像中各种不同的物体特征进行定量化描述后,将其所期望获得的目标物进行提取,并且对所提取的目标物进行一定的定量分析。
2. 什么是图像识别与理解?图像识别与理解是指通过对图像中各种不同的物体特征进行定量化描述后,将其所期望获得的目标物进行提取,并且对所提取的目标物进行一定的定量分析。
比如要从一幅照片上确定是否包含某个犯罪分子的人脸信息,就需要先将照片上的人脸检测出来,进而将检测出来的人脸区域进行分析,确定其是否是该犯罪分子。
5. 简述图像几何变换与图像变换的区别。
①图像的几何变换:改变图像的大小或形状。
比如图像的平移、旋转、放大、缩小等,这些方法在图像配准中使用较多。
②图像变换:通过数学映射的方法,将空域的图像信息转换到频域、时频域等空间上进行分析。
比如傅里叶变换、小波变换等。
第二章图像的基本概念一.填空题1. 量化可以分为均匀量化和非均匀量化两大类。
2. 采样频率是指一秒钟内的采样次数。
3. 图像因其表现方式的不同,可以分为连续图像和离散图像两大类。
3.5. 对应于不同的场景内容,一般数字图像可以分为二值图像、灰度图像和彩色图像三类。

20130917题目求证:在矩阵的LU 分解中,111n n Tn ij i j j i j L I e e α-==+⎛⎫=- ⎪⎝⎭∑∑证明:在高斯消去过程中,假设0jj a ≠ ,若a=0,可以通过列变换使得前面的条件成立,这里不考虑这种情况。
对矩阵A 进行LU 分解,()()()()()1111111L M n M M M n ---=-=∙∙-………… ,其中()1n Tn ij i j i j M j I e e α=+⎛⎫=+ ⎪⎝⎭∑ ,i e 、j e 为n 维线性空间的自然基。
()M j 是通过对单位阵进行初等变换得到,通过逆向的变换则可以得到单位阵,由此很容易得到()M j 的逆矩阵为1n Tn ij i j i j I e e α=+⎛⎫- ⎪⎝⎭∑。
故111n n T n ij i j n j i j L I e e I α-==+⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭∏∑上式中的每一项均是初等变换,从右向左乘,则每乘一次相当于对右边的矩阵进行一次向下乘法叠加的初等变换。
由于最初的矩阵为单位阵,变换从右向左展开,因而每一次变换不改变已经更新的数据,既该变换是从右向左一列一列更新数据,故11nn Tn ij i j j i j L I e e α==+⎛⎫=- ⎪⎝⎭∑∑。
数学证明:1nTi j i ji j ee α=+⎛⎫ ⎪⎝⎭∑具有,000n j jA -⎛⎫ ⎪⎝⎭ 和1,1000n j n j B -+-+⎛⎫⎪⎝⎭ 的形式,且有+1,-11,10000=000n j j n j n j AB --+-+⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭ 而11n n T ij i j j k i j e e α-==+⎛⎫ ⎪⎝⎭∑∑具有1,1000n k n k B -+-+⎛⎫⎪⎝⎭的形式,因此:1311111211121==n n n n n n T T T n ij i j n ij i j n ik i k j i j j i j k n i k n n T n i i n ik i i i k L I e e I e e I e e I e e I e ααααα---==+==+=-=+==+⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=---⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫⎛⎫=-- ⎪ ⎪ ⎝⎭⎝⎝⎭∏∑∏∑∑∑∑∑……11211n n n T Tk n ik i kk k i k e I e e α--===+⎛⎫⎛⎫=- ⎪⎪ ⎪⎭⎝⎭⎝⎭∑∑∑#20130924题目一问:能否用逐次householder 相似变换变实矩阵A 为上三角矩阵,为什么?解:不能用逐次householder 相似变换变A 为上三角矩阵,原因如下:A 记作:()12=,,n A a a a ……, ,存在householder 阵1H s.t. 1111H a e α= ,则()()()111111111111111111111,,,0T Th H AH H a A H e H A H e H A H h H A H ααα⎛⎫'''=== ⎪⎪'⎝⎭⎛⎫''=+ ⎪ ⎪⎝⎭11H A H ''第一列的元素不能保证为1e 的倍数,故无法通过householder 变换实现上三角化。

计算机视觉笔试题目及答案大全计算机视觉作为一门交叉学科,涵盖了图像处理、模式识别、机器学习等多个领域。
在计算机视觉的研究和应用过程中,人们需要掌握一些专业知识和技能。
为了帮助读者更好地了解和学习计算机视觉,下面将提供一些常见的计算机视觉笔试题目及其答案。
一、图像处理部分1. 请简要解释图像处理的概念及其应用领域。
图像处理是指对数字图像进行各种操作和处理的技术。
它涵盖了图像增强、图像压缩、图像复原、图像分割、图像识别等多个方面。
在医学影像、安防监控、无人驾驶、图像搜索等领域都有广泛的应用。
2. 图像分割是指什么?请简要介绍一种常见的图像分割方法。
图像分割是将图像划分成若干个子区域的过程。
其中,常见的方法是基于阈值分割。
该方法通过设定一个或多个阈值,将图像中的像素划分为不同的区域。
通过调整阈值的大小,可以获得不同的分割结果。
3. 请简要介绍一种常见的图像增强方法。
直方图均衡化是一种常见的图像增强方法。
该方法通过对图像的像素值进行统计,然后调整像素值的分布,使得图像的对比度得到增强。
直方图均衡化可以改善图像的亮度分布,使得细节更加清晰。
二、模式识别部分1. 请解释模式识别的概念及其应用领域。
模式识别是指通过对给定数据进行分析,自动识别和分类不同的模式或对象的过程。
它可以应用于手写数字识别、人脸识别、语音识别等领域。
2. 请简要介绍一种常见的模式识别算法。
支持向量机(SVM)是一种常见的模式识别算法。
该算法通过将样本映射到高维空间,然后在该空间中找到一个最优的超平面,实现对不同类别的样本进行分类。
SVM在二分类和多分类问题上都具有较好的性能。
3. 请解释神经网络的概念及其应用领域。
神经网络是一种模拟人脑神经元工作原理的计算模型。
它由神经元和连接权值构成,通过输入与输出之间的连接,实现对信息的建模和处理。
神经网络在语音识别、图像分类、自然语言处理等领域有广泛的应用。
三、机器学习部分1. 请解释机器学习的概念及其应用领域。
高等应用数学问题MATLAB 求解习题参考解答(薛定宇著)目录第1 章计算机数学语言概述2第2 章MATLAB 语言程序设计基础5第3 章微积分问题的计算机求解17第4 章线性代数问题的计算机求解29第5 章积分变换与复变函数问题的计算机求解43第6 章代数方程与最优化问题的计算机求解53第7 章微分方程问题的计算机求解71第8 章数据插值、函数逼近问题的计算机求解93第9 章概率论与数理统计问题的计算机求解114第10 章数学问题的非传统解法127第A章自由数学语言Scilab 简介136第1 章计算机数学语言概述1 在你的机器上安装MATLAB 语言环境,并键入demo 命令,由给出的菜单系统和对话框原型演示程序,领略MATLAB 语言在求解数学问题方面的能力与方法。
【求解】在MATLAB 提示符>> 下键入demo 命令,则将打开如图1-1 所示的窗口,窗口左侧的列表框可以选择各种不同组合的演示内容。
图1-1 MATLAB 演示程序界面例如,用户选择MATLAB ! Graphics ! Volume Vlsulization 演示,则将得出如图1-2 所示的演示说明,单击其中的Run this demo 栏目,则将得出如图1-3 所示的演示界面。
用户可以在该界面下按按钮,逐步演示相关内容,而实现这样演示的语句将在该程序界面的下部窗口中给出。
2 作者用MATLAB 语言编写了给出例子的源程序,读者可以自己用type 语句阅读一下源程序,对照数学问题初步理解语句的含义,编写的源程序说明由下表列出。
第1 章计算机数学语言概述3图1-2 MATLAB 演示程序界面举例序号文件名程序说明例1.1 c1ex1.m 利用MATLAB 的符号运算工具箱求解微分问题例1.2 c1ex2.m 分别利用MATLAB 的符号运算工具箱和数值运算功能求解多项式方程,其中用数值方法得出的结果有误差例1.3 c1ex3.m 分别利用MATLAB 的符号运算工具箱和数值运算功能计算Hilbert 矩阵的行列式,其中用数值方法得出的结果有很大误差例1.4 c1ex4.m 令x1 = y; x2 = y_,则可以将原来的二阶微分方程转换成一阶微分方程组,然后就可以求解微分方程的数值解了,原方程是非线性微分方程,故不存在解析解。
第1部分方法介绍奇异值分解(SVD )定理:设m n A R ⨯∈,则存在正交矩阵m m V R ⨯∈和n n U R ⨯∈,使得TO A V U O O ∑⎡⎤=⎢⎥⎣⎦其中12(,,,)r diag σσσ∑= ,而且120r σσσ≥≥≥> ,(1,2,,)i i r σ= 称为A 的奇异值,V 的第i 列称为A 的左奇异向量,U 的第i 列称为A 的右奇异向量。
注:不失一般性,可以假设m n ≥,(对于m n <的情况,可以先对A 转置,然后进行SVD 分解,最后对所得的SVD 分解式进行转置,就可以得到原来的SVD 分解式)方法1:传统的SVD 算法主要思想:设()m n A R m n ⨯∈≥,先将A 二对角化,即构造正交矩阵1U 和1V 使得110T B n U AV m n⎡⎤=⎢⎥-⎣⎦其中1200n n B δγγδ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦然后,对三角矩阵T T B B =进行带Wilkinson 位移的对称QR 迭代得到:T B P BQ =。
当某个0i γ=时,B 具有形状12B O B O B ⎡⎤=⎢⎥⎣⎦,此时可以将B 的奇异值问题分解为两个低阶二对角阵的奇异值分解问题;而当某个0i δ=时,可以适当选取'Given s 变换,使得第i 行元素全为零的二对角阵,因此,此时也可以将B 约化为两个低阶二对角阵的奇异值分解问题。
在实际计算时,当i B δε∞≤或者()1j j j γεδδ-≤+(这里ε是一个略大于机器精度的正数)时,就将i δ或者i γ视作零,就可以将B 分解为两个低阶二对角阵的奇异值分解问题。
主要步骤:(1)输入()m n A R m n ⨯∈≥及允许误差ε(2)计算Householder 变换1,,,n P P ⋅⋅⋅,12,,n H H -⋅⋅⋅,使得112()()0Tn n B nP P A H H m n -⎡⎤⋅⋅⋅⋅⋅⋅=⎢⎥-⎣⎦其中1200n n B δγγδ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 12:n U PP P =⋅⋅⋅,122:.n V H H H -=⋅⋅⋅ (3)收敛性检验:(i )将所有满足()1j j j γεδδ-≤+的j γ置零;(ii )如果0,2,,j j n γ== ,则输出有关信息结束;否则,1:0γ=,确定正整数p q <,使得10p q n γγγ+==⋅⋅⋅==,0j γ≠,p j q <≤;(iii )如果存在i 满足1p i q ≤≤-使得i B δε∞≤,则:0i δ=,1:i x γ+=,1:i y δ+=,1:0i γ+=,:1l =,转步(iv );否则转步(4) (iv )确定cos ,sin c s θθ==和σ使0c s x s c y σ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦这也相应于0Tc s y s c x σ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦所以可以直接调用'Given s 变换算法得到:i l δσ+=,:(,,)T U UG i i l θ=+这相当于(1:;,)(1:;,)(1:;,)Tc s c s U n i i l U n i i l U n i i l s c s c -⎡⎤⎡⎤+=+=+⎢⎥⎢⎥-⎣⎦⎣⎦(v )如果l q i <-,则1:i l x s γ++=,11:i l i l c γγ++++=,1:i l y δ++=,:1l l =+转步(iv ),否则转步(i )(4)构造正交阵P 和Q ,使12=T P B Q B 仍为上双对角阵,其中112100pp p p q q B δγδγγδ+++⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦, 得121:=T B B P B Q =,:(,,)p n p q U Udiag I P I --=,:(,,)p n p q V Vdiag I Q I --=然后转步(3)。
计算机视觉试题及答案
选择题
在计算机视觉中,用于描述图像中像素点亮度变化的是?
A.梯度(正确答案)
B.直方图
C.特征点
D.边缘
下列哪种技术常用于图像分割,将图像划分为多个区域?
A.滤波
B.阈值分割(正确答案)
C.边缘检测
D.特征匹配
在计算机视觉中,用于描述图像局部特征,常用于物体识别和匹配的是?
A.SIFT特征(正确答案)
B.直方图均衡化
C.图像金字塔
D.形态学操作
下列哪个不是计算机视觉中的常见任务?
A.图像分类
B.目标检测
C.图像压缩(正确答案)
D.姿态估计
在进行图像匹配时,常用于比较两个图像之间相似度的是?
A.模板匹配
B.特征点匹配(正确答案)
C.图像增强
D.图像复原
在计算机视觉中,用于从图像中提取出感兴趣区域(ROI)的技术是?
A.区域生长
B.图像分割(正确答案)
C.边缘检测
D.形态学滤波
下列哪种算法常用于图像去噪,通过滤除高频噪声来平滑图像?
A.高斯滤波(正确答案)
B.边缘检测
C.阈值分割
D.特征提取
在计算机视觉中,用于描述图像全局特征,常用于图像检索和分类的是?
A.边缘特征
B.纹理特征
C.直方图特征(正确答案)
D.关键点特征
下列哪个不是计算机视觉在自动驾驶中的常见应用?
A.障碍物检测
B.车道线识别
C.天气预报(正确答案)
D.行人检测。
数字图像处理实践与挑战考试(答案见尾页)一、选择题1. 数字图像处理的基本步骤包括哪些?A. 图像获取、滤波、增强、复原、编码与解码B. 图像变换、空间滤波、频率域处理、图像分割、形态学操作C. 图像平滑、锐化、边缘检测、图像特征提取、图像分类与识别D. 图像编码、解码、图像重建、图像融合、图像超分辨率2. 在数字图像处理中,线性滤波器的主要作用是什么?A. 去除图像中的噪声B. 提高图像的对比度C. 强化图像的边缘信息D. 对图像进行局部调整3. 以下哪种图像处理技术可以用于测量和分析图像中物体的尺寸和形状?A. 图像分割B. 图像变换C. 图像特征提取D. 图像编码和解码4. 在数字图像处理中,直方图均衡化是一种常用的图像增强方法,它的作用是:A. 自适应调整图像的亮度范围B. 根据图像的内容分布调整图像的对比度C. 针对图像中的特定颜色通道进行增强D. 有针对性地增强图像中的高频成分5. 数字图像处理中,频域滤波器的主要作用是什么?A. 对图像进行低通滤波,去除高频噪声B. 对图像进行高通滤波,保留高频信息C. 对图像进行带通或带阻滤波,根据需要选择特定的频率范围D. 对图像进行平均滤波,降低图像的噪声6. 在数字图像处理中,图像配准的目的是什么?A. 将不同时间、不同传感器或不同视角获取的图像统一到同一坐标系下B. 对图像进行缩放、旋转和扭曲等变换C. 提取图像中的关键信息,如特征点、纹理等D. 对图像进行去噪、增强等预处理操作7. 数字图像处理中,卷积运算的意义是什么?A. 实现图像的平滑处理B. 实现图像的锐化处理C. 对图像进行空间域滤波D. 对图像进行频率域滤波8. 在数字图像处理中,二值图像处理的重要应用之一是:A. 图像识别B. 图像分割C. 图像恢复D. 图像增强9. 数字图像处理中,关于图像编码的说法,正确的是:A. 编码可以提高图像的质量B. 编码可以减少图像的数据量C. 编码是一种无损的图像处理方法D. 编码只能是整数精度10. 在数字图像处理中,为了增强图像的边缘信息,应该使用哪种滤波器?A. 径向基函数滤波器(RBF)B. 高斯滤波器C. 椭圆卷积滤波器D. 平滑滤波器11. 数字图像处理的基本步骤包括哪些?A. 图像获取、增强、滤波、转换和显示B. 图像分割、特征提取、匹配、分类和识别C. 图像编码和解码、图像变换、图像恢复D. 图像滤波、图像压缩、图像融合、图像增强12. 在数字图像处理中,滤波器的主要作用是什么?A. 去除图像中的噪声B. 提高图像的分辨率C. 增强图像的边缘信息D. 提取图像中的特定颜色成分13. 以下哪个选项不是图像分割中常用的技术?A. 阈值分割B. 区域生长C. 分水岭算法D. 卷积神经网络14. 在图像特征提取中,以下哪种方法不是常用的特征描述符?A. HOG(方向梯度直方图)B. SIFT(尺度不变特征变换)C. SURF(加速稳健特征)D. 灰度共生矩阵15. 在图像识别中,以下哪种算法是常用的模式识别方法?A. K-均值聚类B. 支持向量机C. 决策树D. 深度学习中的卷积神经网络16. 在数字图像处理中,如何调整图像的对比度和亮度?A. 使用直方图均衡化B. 使用曝光度校正C. 使用饱和度调整D. 使用伽马校正17. 在图像压缩中,以下哪种方法属于有损压缩?A. JPEGB. PNGC. GIFD. TIFF18. 数字图像处理中,如何实现图像的旋转和翻转?A. 使用仿射变换B. 使用旋转矩阵C. 使用极坐标变换D. 使用样条插值19. 在图像融合中,以下哪种技术通常用于提高图像的质量?A. 加权平均法B. 空间域融合C. 频率域融合D. 混合图章法20. 在数字图像处理中,如何处理图像中的异常值?A. 使用中值滤波B. 使用高斯滤波C. 使用局部均值替换D. 使用基于模型的异常检测方法21. 数字图像处理的基本步骤包括哪些?A. 图像获取、滤波、增强、复原、编码与解码B. 图像变换、空间域处理、频率域处理、图像分割、形态学操作C. 图像增强、边缘检测、图像锐化、图像融合、图像压缩D. 图像重建、图像分类、图像识别、图像生成、图像检索22. 在数字图像处理中,常用的图像格式有哪些?A. JPEG、PNG、BMP、GIF、TIFFB. PDF、EPS、PSD、AI、SVGC. BMP、GIF、JPEG、PNG、WebPD. JPEG、PNG、BMP、GIF、TIFF23. 以下哪个选项不是图像平滑滤波器的作用?A. 去除图像中的高频噪声B. 减少图像的细节和边缘信息C. 改善图像的质量和降低模糊度D. 防止图像失真24. 在图像编码过程中,以下哪种方法可以用来降低图像数据量?A. 采用更高的采样率B. 使用无损压缩算法C. 减少图像中的颜色数量D. 对图像进行锐化处理25. 以下哪个因素会影响图像的分辨率?A. 图像的宽度B. 图像的高度C. 图像的色彩深度D. 图像的压缩格式26. 在数字图像处理中,如何通过算法实现图像的旋转?A. 对图像进行线性变换B. 对图像进行非线性变换C. 对图像进行仿射变换D. 对图像进行位图转换27. 在图像分割中,以下哪种方法通常用于将图像划分为多个区域?A. 边缘检测B. 阈值分割C. 区域生长D. 深度学习方法28. 在数字图像处理中,如何实现图像的缩放?A. 对图像进行缩放变换B. 对图像进行平移变换C. 对图像进行旋转变换D. 对图像进行错切变换29. 在图像处理中,如何消除图像中的噪声?A. 使用高通滤波器B. 使用低通滤波器C. 使用中值滤波器D. 使用平均滤波器30. 在数字图像处理中,如何实现图像的锐化?A. 对图像进行高斯模糊B. 对图像进行拉普拉斯算子运算C. 对图像进行双边滤波D. 对图像进行锐化处理算法31. 数字图像处理的基本步骤包括哪些?A. 图像获取、滤波、增强、复原、编码与解码B. 图像分割、特征提取、匹配、分类与识别C. 图像变换、形态学操作、代数运算、逻辑运算D. 图像融合、超分辨率重建、图像压缩32. 在数字图像处理中,如何选择合适的滤波器?A. 根据图像的信噪比选择滤波器类型B. 根据图像的噪声特性选择滤波器类型C. 根据处理目的选择滤波器类型D. 根据图像的分辨率选择滤波器类型33. 以下哪种图像处理技术可以用于边缘检测?A. 均值滤波B. 最大值滤波C. 边缘检测算子D. 图像锐化34. 在图像分割中,以下哪种方法通常用于将图像分为多个区域?A. 阈值分割B. 区域生长C. 分水岭算法D. 深度学习方法35. 在数字图像处理中,如何评估处理效果?A. 通过计算处理前后图像的均方误差(MSE)B. 通过计算处理前后图像的相关系数C. 通过计算处理前后图像的峰值信噪比(PSNR)D. 通过计算处理前后图像的斯皮尔曼等级相关系数(SROCC)36. 在图像编码中,以下哪种方法可以用于降低图像数据量?A. 霍夫曼编码B. LZW编码C. JPEG编码D. 运行长度编码37. 在深度学习应用于图像处理中,卷积神经网络(CNN)的主要优点是什么?A. 可以自动提取图像特征B. 计算复杂度低C. 不需要人工设计特征提取器D. 可以处理大规模图像数据38. 在数字图像处理中,如何处理图像中的噪声?A. 使用高斯滤波B. 使用中值滤波C. 使用双边滤波D. 使用形态学操作39. 在图像融合中,以下哪种方法可以实现多源图像信息的有效组合?A. 使用加权平均法B. 使用最大值法C. 使用最小值法D. 使用主成分分析(PCA)40. 在数字图像处理中,如何实现图像的超分辨率重建?A. 使用基于插值的重建方法B. 使用基于学习的方法,如SRCNNC. 使用基于稀疏表示的方法,如LBPD. 使用基于深度学习的方法,如ESPCN二、问答题1. 数字图像处理的基本步骤包括哪些?2. 如何选择合适的图像处理技术?3. 什么是图像变换?它的主要目的是什么?4. 如何评估数字图像处理算法的性能?5. 什么是图像分割?它的主要应用场景有哪些?6. 什么是图像配准?它在遥感图像处理中的应用是什么?7. 什么是图像修复?它在艺术和文化遗产保护中的应用是什么?8. 什么是深度学习在数字图像处理中的应用?举例说明。