不考虑交互作用的正交试验设计041019200448
- 格式:ppt
- 大小:388.00 KB
- 文档页数:4

正交实验设计当析因设计要求的实验次数太多时,一个非常自然的想法就是从析因设计的水平组合中,选择一部分有代表性水平组合进行试验。
因此就出现了分式析因设计(fractional factorial designs),但是对于试验设计知识较少的实际工作者来说,选择适当的分式析因设计还是比较困难的。
正交试验设计(Orthogonal experimental design)是研究多因素多水平的又一种设计方法,它是根据正交性从全面试验中挑选出部分有代表性的点进行试验,这些有代表性的点具备了“均匀分散,齐整可比”的特点,正交试验设计是分式析因设计的主要方法。
是一种高效率、快速、经济的实验设计方法。
日本著名的统计学家田口玄一将正交试验选择的水平组合列成表格,称为正交表。
例如作一个三因素三水平的实验,按全面实验要求,须进行33=27种组合的实验,且尚未考虑每一组合的重复数。
若按L9(3)3正交表按排实验,只需作9次,按L18(3)7正交表进行18次实验,显然大大减少了工作量。
因而正交实验设计在很多领域的研究中已经得到广泛应用。
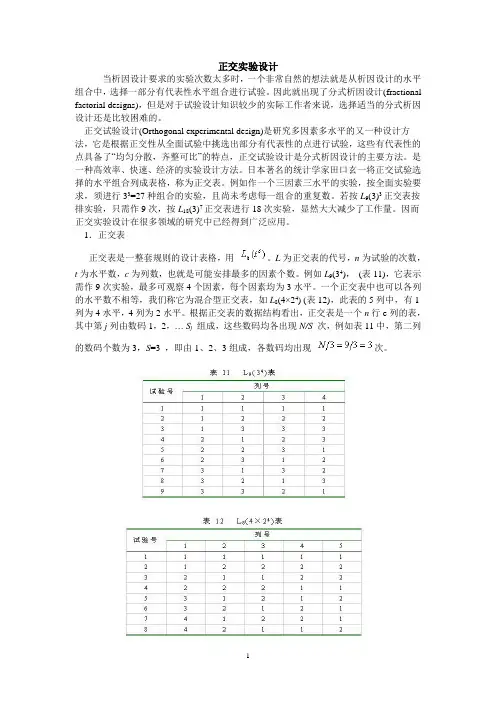
1.正交表正交表是一整套规则的设计表格,用。
L为正交表的代号,n为试验的次数,t为水平数,c为列数,也就是可能安排最多的因素个数。
例如L9(34),(表11),它表示需作9次实验,最多可观察4个因素,每个因素均为3水平。
一个正交表中也可以各列的水平数不相等,我们称它为混合型正交表,如L8(4×24) (表12),此表的5列中,有1列为4水平,4列为2水平。
根据正交表的数据结构看出,正交表是一个n行c列的表,其中第j列由数码1,2,… S j组成,这些数码均各出现N/S次,例如表11中,第二列的数码个数为3,S=3 ,即由1、2、3组成,各数码均出现次。
正交表具有以下两项性质:(1)每一列中,不同的数字出现的次数相等。
例如在两水平正交表中,任何一列都有数码“1”与“2”,且任何一列中它们出现的次数是相等的;如在三水平正交表中,任何一列都有“1”、“2”、“3”,且在任一列的出现数均相等。


试验设计类型之无法考察交互作用的多因素设计:交叉设计胡完;胡良平【摘要】本文目的是介绍一种无法考察交互作用的多因素设计类型,即交叉设计.通过详细介绍与交叉设计类型对应的"主要内容""操作方法"和"设计变形",全面展示了这种设计类型的核心内容、要领和注意事项,为用户正确、合理地选用交叉设计类型创造了有利的条件.%The purpose of this paper was to introduce a kind of design type of multifactor, that was a crossover design, which can't be used to study in the situation with interactions among factors.The core contents, essentials and precautions of the crossover design was demonstrated comprehensively through definitely introducing the main contents, operation methods and deformed designs corresponding with the crossover design.The favorable conditions were created for users to choose the crossover design correctly and reasonably.【期刊名称】《四川精神卫生》【年(卷),期】2017(030)002【总页数】4页(P101-104)【关键词】试验因素;区组因素;样本含量;单个体型;多个体型;交叉设计【作者】胡完;胡良平【作者单位】军事医学科学院生物医学统计学咨询中心,北京 100850;军事医学科学院生物医学统计学咨询中心,北京 100850;世界中医药学会联合会临床科研统计学专业委员会,北京 100029【正文语种】中文【中图分类】R195.1【例1】某麻醉科医生研究催醒宁对氟呱啶的作用,做了一个试验,其格式见表1。



§6.5 不考虑交互作用的正交试验设计下面我们先来看一种比较简单的情形,即不考虑因子之间交互作用的情形。
不考虑交互作用的正交试验设计和数据处理,可按下列步骤进行:(1)选正交表 。
)(mn r L 选择的原则是: 要等于因子的水平数; 要大于或等于因子的个数; 是试验r m n 次数,要尽可能小。
例如,问题中有4个因子,每个因子都是2个水平。
选正交表时,首先要选 =2 的r 表。
这样的正交表有 。
在 中,=3 ,小于因子的 ),2(),2(),2(15167834L L L )2(34L m 个数4,所以不符合要求。
在 中, ,大于因子的个数 ),2(),2(151678L L ,15,7=m 4,符合要求。
在符合要求的正交表中,还要选试验次数 尽可能小的那一个表。
显然,n 在 中,=8 为最小,所以,我们最后选定正交表 。
)2(78L n )2(78L (2)设计表头。
将各因子安排在正交表的各列上方,每个因子占1列,这称为表头。
在不考虑交互作用的正交试验设计中,表头上的因子可以任意安放。
表头上不放因子的列,称为空白列。
(3)按照设计做试验,取得试验观测值。
正交表的每一行代表一种水平组合,对每一种水平组合做一次试验。
按照第 行的k 水平组合所做的第 次试验,所得到的观测值记为 。
正交表有 行,所以,一共k k X n 要做 次试验,共得到 个试验观测值: 。
n n n X X X ,,,21 (4)在正交表的每一列中,求出与各水平对应的均值,以及这一列的平方和。
设我们考虑的是第 列。
在这一列中,表示水平的数字 ,每一个都重j r ,,2,1 复出现 次。
设与这一列中的数字 对应的那几行的试验观测值之和为 ,与这r n 1j W 1一列中的数字 对应的那几行的试验观测值之和为 , ,与这一列中的数字 2j W 2 r 对应的那几行的试验观测值之和为 。
将 分别除以 ,就得j r W j r j j W W W ,,,21 r n 到与这一列中各水平对应的均值 。

实验设计方法—正交实验法概述正交实验法就是利用排列整齐的表-正交表来对试验进行整体设计、综合比拟、统计分析,实现通过少数的实验次数找到较好的生产条件,以到达最高生产工艺效果。
正交表能够在因素变化范围内均衡抽样,使每次试验都具有较强的代表性,由于正交表具备均衡分散的特点,保证了全面实验的某些要求,这些试验往往能够较好或更好的到达实验的目的。
正交实验设计包括两局部内容:第一,是怎样安排实验;第二,是怎样分析实验结果。
正交试验设计法的根本思想正交试验设计法,就是使用已经造好了的表格--正交表--来安排试验并进行数据分析的一种方法。
它简单易行,计算表格化,使用者能够迅速掌握。
下边通过一个例子来说明正交试验设计法的根本想法。
[例1]为提高某化工产品的转化率,选择了三个有关因素进行条件试验,反响温度(A),反响时间(B),用碱量(C),并确定了它们的试验范围:A:80-90℃B:90-150分钟C:5-7%试验目的是搞清楚因子A、B、C对转化率有什么影响,哪些是主要的,哪些是次要的,从而确定最适生产条件,即温度、时间及用碱量各为多少才能使转化率高。
试制定试验方案。
这里,对因子A,在试验范围内选了三个水平;因子B和C也都取三个水平:A:Al=80℃,A2=85℃,A3=90℃B:Bl=90分,B2=120分,B3=150分C:Cl=5%,C2=6%,C3=7%当然,在正交试验设计中,因子可以是定量的,也可以是定性的。
而定量因子各水平间的距离可以相等,也可以不相等。
这个三因子三水平的条件试验,通常有两种试验进行方法:(Ⅰ)取三因子所有水平之间的组合,即AlBlC1,A1BlC2,A1B2C1,……,A3B3C3,共有33=27次试验。
用图表示就是图1 立方体的27个节点。
这种试验法叫做全面试验法。
全面试验对各因子与指标间的关系剖析得比拟清楚。
但试验次数太多。
特别是当因子数目多,每个因子的水平数目也多时。
试验量大得惊人。



试验一、正交试验设计及结果分析一、正交试验设计及极差分析1、在猕猴桃果茶的研制中,为寻找最好的配方,进行了调配试验,试验考察的指标由感官标准评定,其因素水平见下表。
试设计一个正交试验求出最好的配方组合。
(无交互作用的)三因素三水平试验。
2、在油炸方便面生产中,主要原料质量和主要工艺参数对产品的质量有影响,今欲通过试验确定最佳生产条件。
根据专业知识和实践经验,确定试验因素和水平见表。
选择L9(3)安排试验方案。
二、方差分析1、不考虑交互作用的正交试验方差分析:在双歧杆菌奶研制中,为选择最佳发酵条件,用L8(27)正交表安排了正交试验,试验因素与水平见表1,其方案和结果见表2,试对试验结果进行方差分析。
(两水平)表2 正交试验设计及结果2、考虑交互作用的正交试验设计运动发酵单细胞菌是一种酒精生产菌,为了确定其发酵培养基的最佳配方,进行了四因素三水平正交试验,试验指标为酒精浓度(g/ml ),试验因素水平见下表。
试对试验结果进行方差分析。
1 2 35 15 250 0.5 1.0025 30 355.06.07.0试验二、部分因子试验设计及结果分析1、在探讨竹叶中黄酮化合物的超声波辅助提取条件过程中,影响提取得率的因素很多,其中溶剂浓度、料液比、提取温度、超声波功率和提取时间等是比较常见需要考虑的因子,因子水平表见表1,请采用Design Expert软件设计两水平5因子的部分试验设计,根据试验要求,请选择16组试验作为设计表。
表1 部分因子水平表2、若所选择的16组试验部分因子设计结果见表2,请根据结果找出影响提取得率的较显著因子,请写出方差分析结果和回归模型方程。
表2 部分因子试验设计及其结果试验三、响应面试验设计及结果优化分析采用两因素五水平的中心组合设计研究胰蛋白酶水解螺旋藻蛋白质时,pH值、酶-底物浓度比(E/S)两因素及二因素间交互作用对水解蛋白收率的影响。
因素编码及试验方案和结果见表1和表2。
实验报告
(与程序设计有关的课程用)
课程名称:实验设计及优化B
实验题目:无交互作用的正交设计
班级学号:
姓名:
成绩:
沈阳理工大学
2012 年11 月26 日
T3
10.
10. 12.
10. 12.
R
由直观看的好条件是3号实验,最有水平组合为A1B3C3,由极差R的大小得到各因素的主次顺序为A>B>C。
2)直观分析得趋势图如下
1
T
2
T
3
T
二.方差分析结果分析
用方差分析得表如下:
实验号 A B C
转化率y%
1 1 1 1
2 1 2 2
3 1 3 3
4 2 1 2
5 2 2 3
6 2 3 1
7 3 1 3
8 3 2 1
9 3 3 2 水平1 10. 水平2 10. 12. 水平3 10. 12. 误差 SS 91. 14. 11. df 2 2 2 8 2 MS 45.
F 68. 11. P 值
(1)计算离差平方和
①总离差平方和 (1)
其中n 是正交表的行数,正交表的每行确定一个实验处理,每个处理得到一个实验数据,共有n 个实验数据,记为了y 1,y 2,…y n 。
,本例n=9。
y 是n 个实验数据的平均值。
②因素的离差平方和。
因素A 的离差平方和为
(2)。