第2章 自由振动分析-1-修改1汇总
- 格式:ppt
- 大小:1.23 MB
- 文档页数:49

第二章单自由度系统振动§1-1 概述单自由度系统的振动理论是振动理论的理论基础。
(1)尽管实际的机械都是弹性体或多自由度系统,然而要掌握多自由度振动的基本规律,就必须先掌握单自由度系统的振动理论。
此外,(2)许多工程技术上的具体振动系统在一定条件下,也可以简化为单自由度振动系统来研究。
[举例如下:]例如:(1)悬臂锤削镗杆;(2)外圆磨床的砂轮主轴;(3)安装在地上的床身等。
[力学模型的简化方法]若忽略这些零部件中的镗杆、主轴和转轴的质量,只考虑它们的弹性。
忽略那些支承在弹性元件上的镗刀头、砂轮、床身等惯性元件的弹性,只考虑它们的惯性。
把它们看成是只有惯性而无弹性的集中质点。
于是,实际的机械系统近似地简化为单自由度线性振动系统的动力学模型。
在实际的振动系统中必然存在着各种阻尼,故模型中用一个阻尼器来表示。
阻尼器由一个油缸和活塞、油液组成。
汽车轮悬置系统等等。
[以上为工程实际中的振动系统]单自由度振动系统——指用一个独立参量便可确定系统位置的振动系统。
所有的单自由度振动系统经过简化,都可以抽象成单振子,即将系统中全部起作用的质量都认为集中到质点上,这个质点的质量m 称为当量质量,所有的弹性都集中到弹簧中,这个弹簧刚度k称为当量弹簧刚度。
以后讨论中,质量就是指当量质量,刚度就是指当量弹簧刚度。
在单自由度振动系统中,质量m、弹簧刚度k、阻尼系数C是振动系统的三个基本要素。
有时在振动系统中还作用有一个持续作用的激振力P。
应用牛顿运动定律,作用于一个质点上所有力的合力等于该质点的质量和该合力方向的加速度的乘积。
(牛顿运动定律)(达伦培尔原理)现取所有与坐标x 方向一致的力、速度和加速度为正,则:kx x C t P xm --= ωsin 0 (牛顿运动定律) (达伦培尔原理:在一个振动体上的所有各力的合力必等于零) (动静法分析:作用在振动体上的外力与设想加在此振动体上的惯性力组成平衡力系)上式经整理得,t P kx x C xm ωsin 0=++ (2.1) 该式就是单自由度线性振动系统的运动微分方程式的普遍式。

第二章自由振动2.1 引言本章讨论1自由度线性系统的自由振动,即振系在受到初始激扰后的振动。
应用牛顿运动定律,列出确定这种振动规律的微分方程,说明其求解方法,得出位移与速度的表达式以及频率与周期的公式。
对理想的无阻尼振系,还应用了能量守恒原理,列出微分方程,或者不通过微分方程而直接导出预率与周期的公式,无阻尼振系的自由振动是简谐运动。
振动一经开始后,就可以无限期地进行,振幅大小不变。
实际的系统都是有阻尼的。
本章中假定阻尼力与相对速度成正比。
如果阻尼达到或大于某一临界值,系统的自由运动就不是振动。
只有阻尼小于临界值,自由振动才可以发生,但这时振系的机械能不断耗散,振幅不断减小,以至振动完全停息。
有阻尼系统的自由振动是衰减振动。
2.2 简谐振动工程中一些简单的振动向题,有时可以简化为图2.2—1所示的弹簧—质量系统的运动问题。
光滑水平面上的小物体,质量为m,由螺旋弹簧连至定点D。
弹簧重量可以不计,在不受力时为长度为0l,轴线成水平。
沿弹簧轴线取坐标轴x,以弹簧不受力时的右端位置O为原点,向右为正。
假定物体只限于沿坐标轴x进行直线运动,则物体在任一瞬时的位置都可以由坐标x完全确定。
这是1自由度系统。
图2.2-1作用于物体的力,除重力与光滑水平面的反力互相抵消外,只有弹簧力。
在原点O,弹簧力等于零,这是物体的静平衡位置。
当物体从这位置偏离x时,设在O的右侧,x有正值,弹簧受拉伸,它作用于物体的力水平朝左;设在O的左侧,x有负值,弹簧受压缩,它作用于物体的力水平朝右。
可见弹簧力总是指向原点O,力图使物体回到静平衡位置,这种力称为恢复力。
假设用手把物体从位置O向右拉至距离x后,使它静止,则在放手后,物体将在弹簧力的作用下向左加速运动;回到位置O时。
弹簧力变为零,但物体具有速度,由于惯性将继续向左运动;越过原点O后,弹簧力使物体减速,直到速度等于零,此时弹簧力又使物体开始向右运动。
这样,物体将在平衡位置的附近进行往复运动。
第二章 旋转机械振动分析基础振动在设备故障诊断中占了很大的比重,是影响设备安全、稳定运行的重要因素。
振动又是设备的“体温计”,直接反映了设备的健康情况,是设备安全评估的重要指标。
一台机组正常运行时,其振动值和振动变化值都应该比较小。
一旦机组振动值变大,或振动变的不稳定,都说明设备出现了一定程度的故障。
第一节 振动分析的基本概念振动是一个动态量。
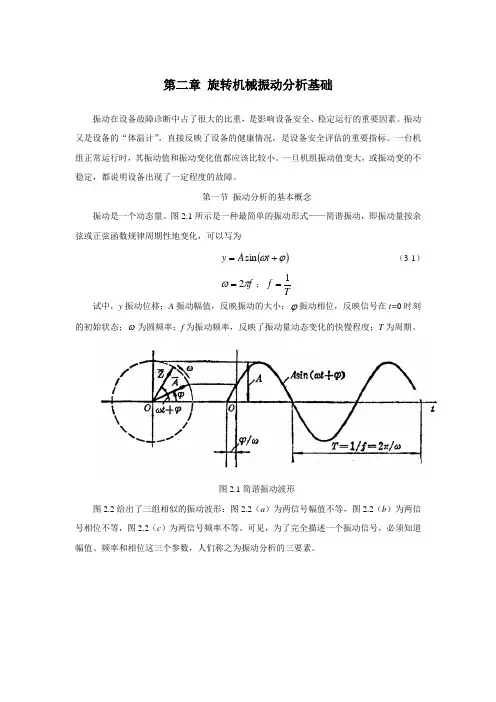
图2.1所示是一种最简单的振动形式——简谐振动,即振动量按余弦或正弦函数规律周期性地变化,可以写为()ϕω+=t A y sin (3-1)f πω2=;Tf 1= 试中,y 振动位移;A 振动幅值,反映振动的大小;ϕ振动相位,反映信号在t=0时刻的初始状态;ω为圆频率;f 为振动频率,反映了振动量动态变化的快慢程度;T 为周期。
图2.1简谐振动波形图2.2给出了三组相似的振动波形:图2.2(a )为两信号幅值不等,图2.2(b )为两信号相位不等,图2.2(c )为两信号频率不等。
可见,为了完全描述一个振动信号,必须知道幅值、频率和相位这三个参数,人们称之为振动分析的三要素。
(a)幅值不等;(b)相位不等;(c)频率不等图2.2 三组相似的振动波型简谐振动时最简单的振动形式,实际发生的振动要比简谐振动复杂的多。
但是根据付立叶变换理论知道,不管振动信号多复杂,都可以将其分解为若干具有不同频率的简谐振动。
图2.3 付立叶变换图解旋转机械振动分析离不开转速,为了方便和直观起见,常以1x表示与转动频率相等的频率,又称为工(基)频,分别以0.5x、2x、3x等表示转动频率的0.5倍、2倍、3倍等相等的频率,又称为半频、二倍频、三倍频。
采用信号分析理论中的快速傅立叶变换可以很方便地求出复杂振动信号所含频率分量的幅值和相位。
目前频谱分析已成为振动故障诊断领域最基本的工具。
频谱分析所起的作用可以概括为以下两点:1)特定故障的频率特征具有必然性。
例如,转子不平衡的频率为工频,气流基振和油膜振荡等故障的频率为低频,电磁激振等故障为高频。




习 题2-1已知系统的弹簧刚度k =800 N/m ,作自由振动时的阻尼振动周期为1.8s ,相邻两振幅的比值12.41=+i i A A ,若质量块受激振力t t F 3cos 360)(=N 的作用,求系统的稳态响应。
解:由题意,可求出系统的运动微分方程为t mxn x p x n 3cos 36022=++ 得到稳态解)3cos(α-=t B x其中m kB B B 45.03604)1(022220==+-=λζλ222122tg λζλωωα-=-=n p n 由d nT i iA A e 2.41===+η489.3π2797.0ln 8.1ln ======dd dd dT p T n T nT ηη 又22n p p n d -=有579.3222=+=n d n p n p p45.51255.1298.0374.0838.01838.0223.02tg 103.1408.045.0838.0223.04)838.01(45.0223.0579.3797.0838.0579.332222===-⨯⨯===⨯⨯+-=======ααζωλB p n p n n所以 x =1.103 cos(3t -51︒27')2-2一个无阻尼弹簧质量系统受简谐激振力作用,当激振频率ω1 =6rad/s 时,系统发生共振;给质量块增加1 kg 的质量后重新试验,测得共振频率ω2 =5.86rad/s ,试求系统原来的质量及弹簧刚度。
解:设原系统的质量为m ,弹簧常数为k 由m kp n =,共振时m kp n ==1ω 所以 mk =6 ①又由 当 86.512=+==m kp n ω ② ①与②联立解出 m =20.69 kg ,k =744.84 N/m2-3总质量为W 的电机装在弹性梁上,使梁产生静挠度st δ,转子重Q ,重心偏离轴线e ,梁重及阻尼可以不计,求转速为ω时电机在垂直方向上稳态强迫振动的振幅。


习 题2-1已知系统的弹簧刚度k =800 N/m ,作自由振动时的阻尼振动周期为1.8s ,相邻两振幅的比值12.41=+i i A A ,若质量块受激振力t t F 3cos 360)(=N 的作用,求系统的稳态响应。
解:由题意,可求出系统的运动微分方程为t mxn x p x n 3cos 36022=++ 得到稳态解)3cos(α-=t B x其中m kB B B 45.03604)1(022220==+-=λζλ222122tg λζλωωα-=-=n p n 由d nT i iA A e 2.41===+η489.3π2797.0ln 8.1ln ======dd dd dT p T n T nT ηη 又22n p p n d -=有579.3222=+=n d n p n p p45.51255.1298.0374.0838.01838.0223.02tg 103.1408.045.0838.0223.04)838.01(45.0223.0579.3797.0838.0579.332222===-⨯⨯===⨯⨯+-=======ααζωλB p n p n n所以 x =1.103 cos(3t -51︒27')2-2一个无阻尼弹簧质量系统受简谐激振力作用,当激振频率ω1 =6rad/s 时,系统发生共振;给质量块增加1 kg 的质量后重新试验,测得共振频率ω2 =5.86rad/s ,试求系统原来的质量及弹簧刚度。
解:设原系统的质量为m ,弹簧常数为k 由m kp n =,共振时m kp n ==1ω 所以 mk =6 ①又由 当 86.512=+==m kp n ω ② ①与②联立解出 m =20.69 kg ,k =744.84 N/m2-3总质量为W 的电机装在弹性梁上,使梁产生静挠度st δ,转子重Q ,重心偏离轴线e ,梁重及阻尼可以不计,求转速为ω时电机在垂直方向上稳态强迫振动的振幅。
第二章自由振动分析2-1(a )由例2 2W Tgk22()W K Tg 因此max()()D t kT 其中k=0、1、2……T D =0.64sec如果很小,T D =T222200()49.9/0.64sec 386/sec kips k kips inin 50/k kips in(b )211ln ln n n v v v v 222121()11.2ln0.3330.86210.05292()10.33320.053025.3%(a ’)21D2T21D TT 249.950/1kkips in(c)2c mW mg2T4cTg21D T T 241WcTg2240.05292000.64sec 386/sec 10.0529kipsc in 0.539sec/ckips inT=T D 0.538sec/ckips in 0.54sec/ckips in2-22k m40 4.472(1/sec )(0)(0)()sin(0)costDDDv v t et v t(0)(0)()sin(0)(0)(0))costDDDv v t et v v v t22(0)(0)()(0)cossinDtDDDv v t ev tt21D()(0)cos(0)(0)sintDDDt ev t v v t2(0)(0)()(0)c o s s i n1tD D v v t ev tt 0.055922(2)(4.47)c c cm(a) c=00D5.6(1)sin 4.470.7cos4.47 1.384.47v t in(1) 5.6cos 4.47 4.47(0.7)sin 4.47 1.69/secv t in (1) 1.4v in ,(1) 1.7/secv in (b) c=2.80.0559(2.8)0.15724.4710.1574.41D(1/sec )(0.157)(4.41)5.60.7(0.157)(4.47)(1)sin 4.410.7cos 4.414.41t e(1)0.764t in(0.157)(4.41)20.157(5.6) 4.41(0.7)(1) 5.6cos 4.41sin 4.4110.157t e (1) 1.10/sect in (1)0.76v in ,(1) 1.1/secv in 第三章谐振荷载反应3-1根据公式有21sin sin 1R t wt wt0.8w w2.778sin 0.8sin1.25R twt wt将t 以80°为增量计算)(t R 并绘制曲线如下:0 80°160°240°320°400°480°560°640°720°800°00.5471.71 -0.481 -3.214 0.357 4.33-0.19 -4.9244.9241.25w wt)(t R3-2解:由题意得:22mkips s in ,20kkips in ,(0)(0)0v v ,w w20 3.162sec2k w rad m8wt(a )0c1sin cos 2R twt wt wt将8wt 代入上式得:()412.566R t (b )0.5ck s in0.50.0395222 3.162cc c c mw1exp1cos exp sin 2R twtwtwt wt将8wt 代入上式得:()7.967R t (c ) 2.0ck s in2.00.158222 3.162cc c c mw1exp1cos exp sin 2R twtwtwt wt将8wt 代入上式得:() 3.105R t 3-3解:(a ):依据共振条件可知:1003860.0810.983sec4000k kg wwrad m W由2LTVw 得:10.9833662.96022wL V ft s(b ):122max2221212tgovv 1w w 0.41.2gov in 代入公式可得:max1.921tv in(c ):2L T Vw45m i n 66Vhf t s226611.51336V wrad secL11.513 1.04810.983w w0.4代入数据得:122max22212=1.85512t govv in3-4解:按照实际情况,当设计一个隔振系统时,将使其在高于临界频率比2下运行,在这种情况下,隔振体系可能有小的阻尼。
《振动力学》——习题第二章 单自由度系统的自由振动2-1 如图2-1 所示,重物1W 悬挂在刚度为k 的弹簧上并处于静止平衡位置,另一重物2W 从高度为h 处自由下落到1W 上且无弹跳。
试求2W 下降的最大距离和两物体碰撞后的运动规律。
解:222221v gW h W =,gh v 22=动量守恒:122122v gW W v g W +=,gh W W W v 221212+=平衡位置:11kx W =,kW x 11=1221kx W W =+,kW W x 2112+=故:kW x x x 21120=-= ()2121W W kgg W W k n +=+=ω故:tv t x txt x x n nn n nn ωωωωωωsin cos sin cos 12000+-=+-=xx 0x 1x 12平衡位置2-2 一均质等直杆,长为l ,重量为w ,用两根长h 的相同的铅垂线悬挂成水平位置,如图2-2所示。
试写出此杆绕通过重心的铅垂轴做微摆动的振动微分方程,并求出振动固有周期。
解:给杆一个微转角θ2aθ=h α2F =mg由动量矩定理:ah a mg a mg Fa M ml I M I 822cos sin 12122-=-≈⋅-====αθαθ其中12cossin ≈≈θααh l ga p ha mg ml n 22222304121==⋅+θθ g h a l ga h l p T n 3π23π2π222===2-3 一半圆薄壁筒,平均半径为R , 置于粗糙平面上做微幅摆动,如图2-3所示。
试求其摆动的固有频率。
图2-3 图2-42-4 如图2-4 所示,一质量m连接在一刚性杆上,杆的质量忽略不计,试求下列情况系统作垂直振动的固有频率:(1)振动过程中杆被约束保持水平位置;(2)杆可以在铅垂平面内微幅转动;(3)比较上述两种情况中哪种的固有频率较高,并说明理由。
图T 2-9 答案图T 2-9解:(1)保持水平位置:m kk n 21+=ω(2)微幅转动:mglllF2112+=mgl1l2xx2xx'mglll2121+=k2k1ml1l2()()()()()()()()()mgk k l l k l k l mgk k l l k l l k l l l k l mg k k l l k l k l l l l k l l mg l mgk l l l k l l l l l l k l l mg l l l l x x k F x x x 2122122212121221221121212221212211211121212122211211121221112111 ++=+-++=+-⋅+++=⎥⎦⎤⎢⎣⎡+-++++=+-+='+=故:()22212121221k l k l k k l l k e++=mk en =ω 2-5 试求图2-5所示系统中均质刚性杆AB 在A 点的等效质量。