- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
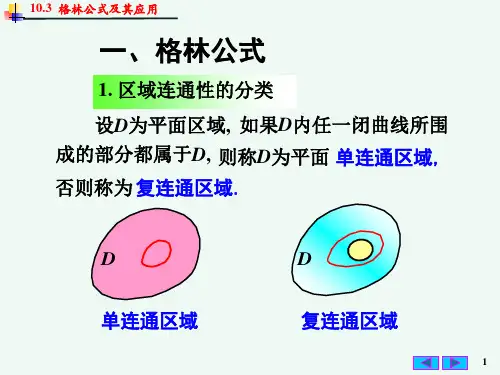
例如: P
y x2 y2
, Q
x x2 y2
,在复连通域
1 2 2 D ( x , y ) x y 4 中,具有连续偏导数, 2
Q y2 x2 P 2 x ( x y 2 )2 y
x y 1
2
2
Pdx Qdy 2 0
2.定理 2
若向量值函数 A( x , y ){ P ( x , y ),Q ( x , y )} 在单连
通域 D 上有一阶连续偏导数,则以下四个命题等价: P Q (1) ( x, y )D ,有 ; y x
(2)沿 D 内任意的逐段光滑闭曲线 C,有
C PdxQdy0 ; Pdx Qdy 与路径无关,只与位于 D 内的 (3 ) C ( AB )
B ( 2,0)
x
kx k (1 y ) y W F ds dx dy C C r3 r3 A (0,1)
其中 C: y 2 x x 2 , x : 20 。
M ( x, y)
o
B ( 2,0)
x
∵ P
kx r3
, Q
k (1 y ) r3
P 3kx(1 y ) Q , , y x r5
其中 C: y 2 x x 2 , x : 20 。
M ( x, y)
o
B ( 2,0)
x
P 3kx(1 y ) Q ∵ P , Q , , y x r3 r3 r5 Q P C OB ( x y )dxdy C OB D OB BO
y
A (0,1)
则 MA{ x,1 y} ,
r MA x 2 (1 y)2 ,
M ( x, y)
o
MA k kx k (1 y ) F F { x, 1 y}{ , }, 3 3 3 r r MA r
B ( 2,0)
x
kx k (1 y ) y W F ds dx dy C C r3 r3 A (0,1)
2u 2u ∵ P,Q 有一阶连续偏导数,即 , 连续, xy yx P Q ∴ 。 y x
Q P 定理 2 表明在单连通域内,若 ,则曲线积分与 x y
路径无关,此时可以选择特殊的路径计算曲线积分。
注意:定理 2 中的区域 D 必须是单连通域,若 D 是
复连通域定理 2 就不一定成立。
0 k (1 y ) ∴W dx dy BO r 3 2 r3
kx
k (1 y )
kx
kx ( x 2 1)
1 dx k (1 )。 3 5 2
xdy ydx 例 2 计算 I 2 ,其中 C 是以点 A( 2, 0) 2 C x 9 y
为圆心,半径为 R( R 2) 的圆周,取逆时针方向。 y x Q 解: P 2 , , x 9 y2 x2 9 y2
( x, y) ( x , y )
Pdx Qdy 。
下面来证明 du Pdx Qdy 。
∵曲线积分与路径无关, ∴取由点 A 到点 B 是沿
y
B( x , y )
C ( x x , y )
任意光滑曲线,点 B 到 点 C 是平行 x 轴的线段。 ∵ u( x x , y ) u( x , y )
0
y
0
y y y 2 2 [arctan ] 0 arctan . x y x x
xdy
设 A( x , y ) 为 D 内一定点,
由于曲线积分与路径无关,故
y
N ( x , y)
B( x, y )
取 AMB 为积分路线,得:
u( x , y )
( x, y)
若 C1与C1 相交,则再引曲 线C 3 ,使 C 3 与 C1 , C 2 均 不 相 交,
由
C1 PdxQdy C3 PdxQdy
C2 PdxQdy C3 PdxQdy
C1 PdxQdy C2 PdxQdy 。
由(3) (4) 。
∵曲线积分与路径无关,
∴取定起点 A( x , y ) D ,曲线积分则是终点( x , y )D 的函数,记为u( x , y ) ,即 u( x , y )
∴曲线积分与路径无关,取直线段 BO 为 积分路径,
0 k (1 y ) ∴W dx dy BO r 3 2 r3
kx
kx ( x 2 1)
1 dx k (1 )。 3 5 2
3.定义 1 若函数 u( x , y ) 的全微分 du Pdx Qdy ,则称
起点 A 与终点 B 有关。
(4)在 D 内存在二元函数u( x , y ) ,使得 du Pdx Qdy 。
证明:由(1) (2) 。 设R 是C 所包围的区域,
∵ D 是单连通域,∴ R D 。 ∵在 R 上有
Q P ∴由 Green 公式得 Pdx Qdy ( )dxdy 0 。 C x y
Q P , x y
由(2) (3) 。
R
A, B D ,以不同的路线C1 , C 2 连结 A 与B 。
①若 C1与C1 不相交,
则 PdxQdy0 , C2 C 1
y A
C1 C2
B
o
x
∴
C2 Pdx Qdy C2 C 1 C1 C 1 Pdx Qdy 。
y x y
2 2
, Q
x x y
2 2
,则有
P y2 x2 Q 在右半平面内恒成立, 2 2 2 y ( x y ) x
y
C ( x, y)
故
xdy ydx x y
2 2
是某个函数的全微分。
取如图所示的积分路线,则有
o
A(1,0)
B( x ,0)
x
( x , y ) xdy ydx xdy ydx xdy ydx u( x , y ) (1,0) x 2 y 2 AB x 2 y 2 BC x 2 y 2
u( x , y ) 是表达式 Pdx Qdy 的一个原函数。
若 P ( x , y ),Q( x , y ) 在单连通域 D 上具有一阶连续偏导数,
P Q 则 Pdx Qdy 在 D 内存在原函数的充要条件是 , y x
且 Pdx Qdy 的所有原函数为
u( x , y )
例 1.设位于点 ( 0, 1) 的质点 A 对质点 M 的引力大小为 k A与 M 之 间 的 距 离) (k 为常数, r 为 质 点 ,质点沿 2 r 曲线 y 2 x x 2 自 B( 2, 0) 运动到O(0, 0) ,求在此运动
中质点 A 对质点 M 的引力所作的功 W。
解:设质点 M 的 位置为( x , y ) ,
2 x
P 2 Q x 且 , y x
y
∴曲线积分 I 与路径无关。
把积分路径改为直线段AO ,
o
A(2,0)x
则 I
0 2
3 xe x dx 3 [ xe x e x ] 0 3 [e2 (1 2)1] 。
2
例 1.设位于点 ( 0, 1) 的质点 A 对质点 M 的引力大小为 k A与 M 之 间 的 距 离) (k 为常数, r 为 质 点 ,质点沿 2 r 曲线 y 2 x x 2 自 B( 2, 0) 运动到O(0, 0) ,求在此运动
1 3 例 3.计算 I ( x y 3 xe )dx ( x ysiny )dy ,其中 C 是 C 3
2 x
摆线 x t sint , y 1 cost 从点 A( 2, 0) 到点 O(0, 0) 的一段弧。
1 3 解: P ( x , y ) x y 3 xe , Q( x , y ) x ysiny , 3 ∵ P ( x , y ), Q( x , y ) 在全平面上连续,
( x, y) ( x , y )
P ( x , y )dx Q( x , y )dy C
其中 C 为任意常数, ( x , y ) D 。
4.定理 3 (曲线积分基本定理)
设 P ( x, y ),Q( x, y ) 在单连通域 D 上连续,若 u( x , y ) 是 Pdx Qdy 的一个原函数,而 A( x1 , y1 ) 和 B( x2 , y2 ) 是 D 内任意两点,则
C : x 2 9 y 2 2 ,则在C与C 所围成的复连通区域 D 上,满足 Green 公 式的条件,得
Q P ( )dxdy 0 , C C C C C C x y x2 9 y2 D y
∴ I
P ( x x, y )x ,0 1 。(积分中值定理)
∵ P ( x , y ) 在点 B ( x , y ) 上连续,
u u( x x , y ) u( x , y ) ∴ lim lim P ( x x , y ) P ( x , y ). x x0 x x0
( x2 , y2 ) Pdx Qdy u( x2 , y2 ) u( x1 , y1 ) u( x , y ) ( x , y ) . C( AB ) 1 1
例 4.验证:
xdy ydx
2 2
x y 的全微分,并求出一个这样的函数。
在右半平面 ( x 0) 内是某个函数
证明:令 P
Q P P 9 y2 x2 Q 0 (( x , y ) (0,0) ) , 。 2 2 2 x y y ( x 9 y ) x
(1)当R 2 时,