正方形判定导学案.

第2课时正方形的判定【课前自主学习】一、目标导读1、知道正方形的判定方法，会运用平行四边形、矩形、菱形、正方形的判定条件进行有关的论证和计算。

2、经历探究正方形判定条件的过程，发展学生初步的综合推理能力，主动探究的学习习惯，逐步掌握说理的基本方法。

3、理解特殊的平行四边形之间的内在联系，培养学生辩证看问题的观点。

学习重点：掌握正方形的判定条件。

学习难点：合理恰当地利用正方形的判定定理解决问题。

二、预习检测我们学习了平行四边形、矩形、菱形、正方形，那么思考一下，它们之间有怎样的包含关系？请填入右图中。

【课堂互动学习】一、旧知补标，查缺补漏（1—5分钟）1.我的错题库：2.温故知新：（1）怎样判定一个四边形是平行四边形？（2）怎样判定一个四边形是矩形？（3）怎样判定一个四边形是菱形？议一议：怎样判定一个四边形是正方形？二、预习反馈，掌握学情（1—5分钟）1.在括号后面打“√”或“×”：（1）自觉阅读课文（），（2）自我完成“预习检测”（）。

2.展示答案，梳理知识（个别提问或集体回答，师生共同完成）。

三、例题变式，方法提炼（10—15分钟）1．探索正方形的判定条件：（1）直接用正方形的定义判，即先判定这个四边形是平行四边形，若这个平行四边形有一个角是直角，并且有一组邻边相等，那么就可以判定这个四边形是正方形；（2）先判定这个四边形是矩形，再判定这个矩形是菱形，那么这个四边形是正方形；（3）先判定这个四边形是菱形，再判定这个菱形是矩形，那么这个四边形是正方形。

2.方法提炼：后两种判定均要用到矩形和菱形的判定定理。

矩形和菱形的判定定理是判定正方形的基础。

这三个方法还可写成：有一个角是直角，且有一组邻边相等的四边形是正方形；有一组邻边相等的矩形是正方形；有一个角是直角的菱形是正方形。

上述三种判定条件是判定四边形是正方形的一般方法，可当作判定定理用，但由于判定平行四边形、矩形、菱形的方法各异，所给出的条件各不相同，所以判定一个四边形是不是正方形的具体条件也相应可作变化，在应用时要仔细辨别后才可以作出判断。

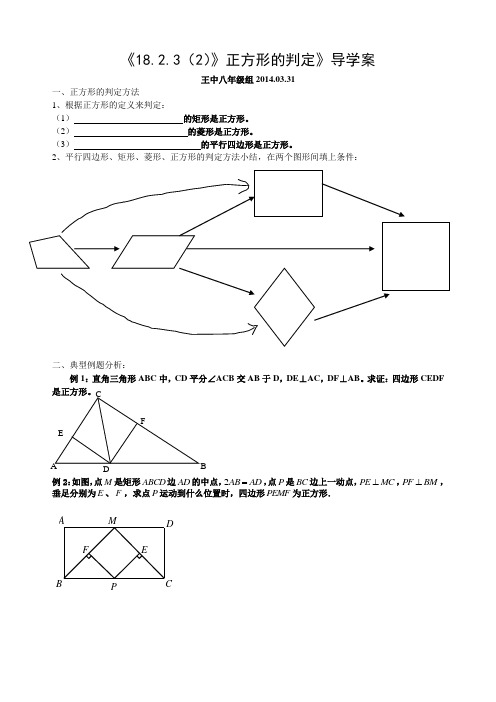
《18.2.3（2）》正方形的判定》导学案
王中八年级组2014.03.31
一、正方形的判定方法
1、根据正方形的定义来判定：
（1） 的矩形是正方形。

（2） 的菱形是正方形。

（3） 的平行四边形是正方形。

2、平行四边形、矩形、菱形、正方形的判定方法小结，在两个图形间填上条件：
二、典型例题分析：
例1：直角三角形ABC 中，CD 平分∠ACB 交AB 于D ，DE ⊥AC ，DF ⊥AB 。

求证：四边形CEDF 例2：如图，点M 是矩形ABCD 边AD 的中点，2AB AD =，点P 是BC 边上一动点，PE MC ⊥，PF BM ⊥，垂足分别为E 、F ，求点P 运动到什么位置时，四边形PEMF 为正方形．
P M F E D C B A
三、练一练：
1、分别延长等腰直角三角形OAB 的两条直角边AO 和BO ，使AO =OC ，BO =OD 求证：四边形ABCD 是正方形。

2、在△ABC 中,AB=AC,D 是BC 的中点，DE ⊥AB ，DF ⊥AC ，垂足分别是E ，F 。

1)试说明：DE=DF
2)只添加一个条件,使四边形EDFA 是正方形.
请你至少写出两种不同的添加方法.(选择其中一种进行证明)
3、已知：如图，在ABC ∆中，AB AC =，AD BC ⊥，垂足为点D ，AN 是ABC ∆外角CAM ∠的平分线，CE AN ⊥，垂足为点E ．
⑴ 求证：四边形ADCE 为矩形；
⑵ 当ABC ∆满足什么条件时，四边形ADCE 是一个正方形？并给出证明．
M
E N
C
D B A C。

第2课时正方形的判定【课前自主学习】一、目标导读1、知道正方形的判定方法，会运用平行四边形、矩形、菱形、正方形的判定条件进行有关的论证和计算。

2、经历探究正方形判定条件的过程，发展学生初步的综合推理能力，主动探究的学习习惯，逐步掌握说理的基本方法。

3、理解特殊的平行四边形之间的内在联系，培养学生辩证看问题的观点。

学习重点：掌握正方形的判定条件。

学习难点：合理恰当地利用正方形的判定定理解决问题。

二、预习检测我们学习了平行四边形、矩形、菱形、正方形，那么思考一下，它们之间有怎样的包含关系？请填入右图中。

【课堂互动学习】一、旧知补标，查缺补漏（1—5分钟）1.我的错题库：2.温故知新：（1）怎样判定一个四边形是平行四边形？（2）怎样判定一个四边形是矩形？（3）怎样判定一个四边形是菱形？议一议：怎样判定一个四边形是正方形？二、预习反馈，掌握学情（1—5分钟）1.在括号后面打“√”或“×”：（1）自觉阅读课文（），（2）自我完成“预习检测”（）。

2.展示答案，梳理知识（个别提问或集体回答，师生共同完成）。

三、例题变式，方法提炼（10—15分钟）1．探索正方形的判定条件：（1）直接用正方形的定义判，即先判定这个四边形是平行四边形，若这个平行四边形有一个角是直角，并且有一组邻边相等，那么就可以判定这个四边形是正方形；（2）先判定这个四边形是矩形，再判定这个矩形是菱形，那么这个四边形是正方形；（3）先判定这个四边形是菱形，再判定这个菱形是矩形，那么这个四边形是正方形。

2.方法提炼：后两种判定均要用到矩形和菱形的判定定理。

矩形和菱形的判定定理是判定正方形的基础。

这三个方法还可写成：有一个角是直角，且有一组邻边相等的四边形是正方形；有一组邻边相等的矩形是正方形；有一个角是直角的菱形是正方形。

上述三种判定条件是判定四边形是正方形的一般方法，可当作判定定理用，但由于判定平行四边形、矩形、菱形的方法各异，所给出的条件各不相同，所以判定一个四边形是不是正方形的具体条件也相应可作变化，在应用时要仔细辨别后才可以作出判断。

新北师大版九年级数学上册1.3.2正方形的判定导学案【教学目标】知识与技能1．能进一步理解掌握正方形的判定定理．2．进一步体会证明的必要性以及计算与证明在解决问题中的作用．过程与方法1．经历探索、猜想、证明的过程，进一步发展推理论证能力．2．进一步体会证明的必要性以及计算与证明在解决问题中的作用． 3．体会证明过程中所运用的归纳概括以及转化等数学思想方法．情感、态度与价值观1．通过知识的迁移、类比、转化，激发学生探索新知识的积极性和主动性． 2．体会数学与生活的联系．【教学重难点】教学重点特殊四边形―― 正方形的判定定理的灵活应用．教学难点特殊四边形―― 正方形的判定定理的灵活应用．【导学过程】【创设情景，引入新课】回顾正方形有哪些性质【自主探究】：自学，明确正方形的性质定理和判定定理的灵活应用．Ⅱ．解决问题：下面大家来猜一猜，想一想依次连接任意四边形各边的中点可以得到一个平行四边形．那么，依次连接正方形各边的中点．(如图)能得到―个怎样的图形呢?先猜一猜，再证明．依次连结正方形各边的中点得到的四边形是正方形．证明：∵四边形ABCD是正方形．∴∠A＝∠B=∠C=∠D＝90°， AB＝BC＝CD＝DA．又∵A1、B1、C1、D1分别是边AB、BC、CD、DA的中点。

∴AA1＝BA＝BB1＝B1C ＝CC1＝C1D＝DD1＝D1A．∴△AD1A1≌△BA1B1≌△CB1C1≌△DC1D1．∴A1B1＝B1C1＝C1D1＝D1A1．∵∠A＝∠B＝90°， AA1＝AD1，A1B=BB1，∴∠AA1D1=∠BA1B1=45°．∴∠D1A1B1＝90°．∴四边形A1B1C1D1是正方形．这个题是先证明了四边形A1B1C1D1的四条边相等，即是菱形，然后又证明了这个四边形的一个角是直角，即有一个角为直角的菱形是正方形，从而得证四边形A1B1C1D1是正方形．【课堂探究】已知:如图,点E，F，G，H分别是正方形ABCD四条边上的点，并且AF= BG= CH= DE。

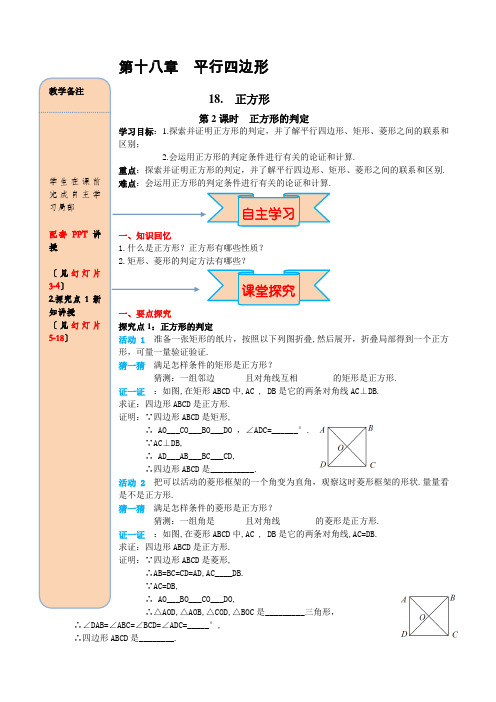
第十八章 平行四边形18. 正方形第2课时 正方形的判定学习目标：1.探索并证明正方形的判定，并了解平行四边形、矩形、菱形之间的联系和区别；2.会运用正方形的判定条件进行有关的论证和计算.重点：探索并证明正方形的判定，并了解平行四边形、矩形、菱形之间的联系和区别. 难点：会运用正方形的判定条件进行有关的论证和计算.一、知识回忆1.什么是正方形？正方形有哪些性质？2.矩形、菱形的判定方法有哪些？一、要点探究探究点1：正方形的判定活动1 准备一张矩形的纸片，按照以下列图折叠,然后展开，折叠局部得到一个正方形，可量一量验证验证.猜一猜 满足怎样条件的矩形是正方形？猜测：一组邻边_______且对角线互相________的矩形是正方形.证一证 ：如图,在矩形ABCD 中,AC , DB 是它的两条对角线AC ⊥DB. 求证：四边形ABCD 是正方形. 证明：∵四边形ABCD 是矩形,∴ AO___CO___BO___DO ，∠ADC=______°. ∵AC ⊥DB,∴ AD___AB___BC___CD,∴四边形ABCD 是__________.活动 2 把可以活动的菱形框架的一个角变为直角，观察这时菱形框架的形状.量量看是不是正方形.猜一猜 满足怎样条件的菱形是正方形？猜测：一组角是_______且对角线________的菱形是正方形.证一证 ：如图,在菱形ABCD 中,AC , DB 是它的两条对角线,AC=DB. 求证：四边形ABCD 是正方形. 证明：∵四边形ABCD 是菱形,∴AB=BC=CD=AD,AC____DB. ∵AC=DB,∴ AO___BO___CO___DO,∴∠DAB=∠ABC=∠BCD=∠ADC=_____°, ∴四边形ABCD 是________.课堂探究自主学习教学备注学生在课前完成自主学习局部配套PPT 讲授〔见幻灯片3-4〕2.探究点1新知讲授〔见幻灯片5-18〕要点归纳：正方形判定的几条途径：1. 一组邻边_______且一内角是__________的平行四边形是正方形；2. 先判断四边形是菱形，再判断一内角是___________；3. 先判断四边形是菱形，再判断对角线____________；4. 先判断四边形是矩形，再判断一组邻边_________；5. 先判断四边形是矩形，再判断对角线相互__________. 典例精析例1在正方形ABCD 中，点E 、F 、M 、N 分别在各边上，且AE=BF=CM=DN ．四边形EFMN 是正方形吗?为什么?分析：由可证△AEN ≌△BFE ≌△CMF ≌△DNM ，得四边形EFMN 是菱形，再证有一个角是直角即可.例 2 如图，在直角三角形中，∠C=90°，∠A 、∠⊥AC ，DF ⊥AB.求证:四边形CEDF 为正方形.例3 如图，EG ,FH 过正方形ABCD 的对角线的交点O,且EG ⊥FH.求证：四边形EFGH 是正方形. 针对训练1.在四边形ABCD 中，O 是对角线的交点，能判定这个四边形是正方形的是〔 〕 A ．AC=BD ，AB ∥CD ，AB=CD B ．AD ∥BC ，∠A=∠C C ．AO=BO=CO=DO ，AC ⊥BD D ．AO=CO ，BO=DO ，AB=BC2.如图，正方形ABCD ，动点E 在AC 上，AF ⊥AC ，垂足为A ，AF=AE ． 〔1〕求证：BF=DE ；〔2〕当点E 运动到AC 中点时(其他条件都保持不变)，问四边形AFBE 是什么特殊四边形？说明理由．3.前面学菱形时我们探究了顺次连接任意四边形各边中点所得的四边形是平行四边形,顺次连接矩形各边中点得到菱形,那么顺次连接正方形各边中点得到怎样的特殊平行四边形？ 二、课堂小结1.以下命题正确的选项是〔 〕2.如图，四边形ABCD 是平行四边形，以下结论中不正确的选项是〔 〕 A ．当AB=BC 时，四边形ABCD 是菱形 B ．当AC ⊥BD 时，四边形ABCD 是菱形 C ．当∠ABC=90°时，四边形ABCD 是矩形 当堂检测教学备注 配套PPT 讲授3.课堂小结〔见幻灯片26〕4.当堂检测 〔见幻灯片19-25〕教学备注 配套PPT 讲授2.探究点1新知讲授〔见幻灯片5-18〕3.如图，四边形ABCD 中，∠ABC=∠BCD=∠CDA=90°，请添加一个条件____________________，可得出该四边形是正方形．4.四边形ABCD 是平行四边形，再从①AB=BC ，②∠ABC=90°，③AC=BD ，④AC ⊥BD 四个条件中，选两个作为补充条件后，使得四边形ABCD 是正方形，其中错误的选项是_________________〔只填写序号〕．5.如图，在四边形ABCD 中, AB=BC ,对角线BD 平分∠ABC , P 是BD 上一点,过点P 作PM ⊥AD , PN ⊥CD ,垂足分别为M 、N. (1) 求证：∠ADB=∠CDB;(2) 假设∠ADC=90,求证：四边形MPND 是正方形.6.如图，△ABC 中，D 是BC 上任意一点，DE ∥AC ，DF ∥AB ． (1)试说明四边形AEDF 的形状，并说明理由．(2)连接AD ，当AD 满足什么条件时，四边形AEDF 为菱形，为什么？(3)在(2)的条件下，当△ABC 满足什么条件时，四边形AEDF 为正方形，不说明理由．第2题图 第3题图 教学备注4.当堂检测 〔见幻灯片19-25〕。

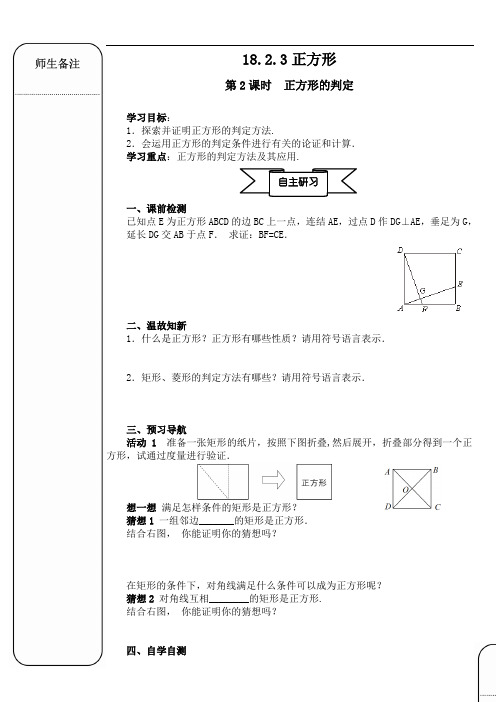
18.2.3正方形第2课时正方形的判定学习目标：1．探索并证明正方形的判定方法.2．会运用正方形的判定条件进行有关的论证和计算．学习重点：正方形的判定方法及其应用.自主研习一、课前检测已知点E为正方形ABCD的边BC上一点，连结AE，过点D作DG⊥AE，垂足为G，延长DG交AB于点F．求证：BF=CE．二、温故知新1．什么是正方形？正方形有哪些性质？请用符号语言表示．2．矩形、菱形的判定方法有哪些？请用符号语言表示．三、预习导航活动1准备一张矩形的纸片，按照下图折叠,然后展开，折叠部分得到一个正方形，试通过度量进行验证．想一想满足怎样条件的矩形是正方形？猜想1 一组邻边_______的矩形是正方形．结合右图，你能证明你的猜想吗？在矩形的条件下，对角线满足什么条件可以成为正方形呢？猜想2 对角线互相________的矩形是正方形.结合右图，你能证明你的猜想吗？四、自学自测在四边形ABCD 中，O是对角线的交点，能判定这个四边形是正方形的是( ) A．AC=BD，AB∥CD，AB=CDB．AD∥BC，∠A=∠CC．AO=BO=CO=DO，AC⊥BDD．AO=CO，BO=DO，AB=BC五、我的疑惑(反思)探究点拨一、要点探究探究点1：正方形的判定方法活动 2 把可以活动的菱形框架的一个角变为直角，观察这时菱形框架的形状．量量看是不是正方形．猜一猜满足怎样条件的菱形是正方形？猜想1：一个角是_______的菱形是正方形．结合右图，你能证明你的猜想吗？在菱形的条件下，对角线满足什么条件可以成为正方形呢？猜想2 对角线________的菱形是正方形.结合右图，你能证明你的猜想吗？要点归纳：正方形判定的几条途径：一、一组邻边_______且一内角是__________的平行四边形是正方形；二、先判断四边形是矩形，再判断一组邻边_________；三、先判断四边形是矩形，再判断对角线相互__________；四、先判断四边形是菱形，再判断一内角是___________；五、先判断四边形是菱形，再判断对角线____________．即学即练如图，在Rt△ABC中，∠C=90°，∠A、∠B的平分线交于点D．DE⊥AC，DF⊥AB．求证:四边形CEDF为正方形．二、精讲点拨例1在正方形ABCD中，点E、F、M、N分别在各边上，且AE=BF=CM=DN．四边形EFMN是正方形吗?为什么?分析：由已知可证△AEN≌△BFE≌△CMF≌△DNM，得四边形EFMN是菱形，再证有一个角是直角即可．例2如图，EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH．求证：四边形EFGH是正方形．三、变式训练如图，正方形ABCD，动点E在AC上，AF⊥AC，垂足为A，且AF=AE．(1)求证：BF=DE；(2)当点E运动到AC中点时(其他条件都保持不变)，问四边形AFBE是什么特殊四边形？说明理由．四、课堂小结星级达标★1.下列命题正确的是( )A ．四个角都相等的四边形是正方形B ．四条边都相等的四边形是正方形C ．对角线相等的平行四边形是正方形D ．对角线互相垂直的矩形是正方形 ★2如右图，已知四边形ABCD 是平行四边形，下列结论中不正确的是( ) A ．当AB=BC 时，四边形ABCD 是菱形 B ．当AC ⊥BD 时，四边形ABCD 是菱形 C ．当∠ABC=90°时，四边形ABCD 是矩形 D ．当AC=BD 时，四边形ABCD 是正方形★3.如上图，在四边形ABCD 中，∠ABC=∠BCD=∠CDA=90°，请再添加一个条件：____________________，使该四边形是正方形．★★4.已知四边形ABCD 是平行四边形，再从①AB=BC ，②∠ABC=90°，③AC=BD ，④AC ⊥BD 四个条件中，选两个作为补充条件后，使得四边形ABCD 是正方形，其中错误的是_________________(只填写序号)．★★5．如图，在四边形ABCD 中, AB=BC ,对角线BD 平分∠ABC , P 是BD 上一点,过点P 作PM ⊥AD , PN ⊥CD ,垂足分别为M 、N ．(1) 求证：∠ADB=∠CDB ；(2) 若∠ADC=90°,求证：四边形MPND 是正方形．★★★6.如图，在正方形ABCD 中，E 是边AB 上一点，延长AD 至点F ，使DF=BE ，连接CF.（1）求证：∠BCE=∠DCF ；（2）过点E 作EG ∥CF ，过点F 作FG ∥CE ，试判断四边形CEGF 的形状，并说明理由.F6题图E DCBA G我的反思（收获，不足）分层作业必做(教材 智慧学习 配套) 选做参考答案：课前检测试题分析：要证明BF ＝CE ，只要证明AF ＝BE 即可，可通过证明△AFD ≌△BEA 得到．证明：在正方形ABCD中，∠DAF＝∠ABE＝90°，DA＝AB＝BC，∵DG⊥AE，∴∠FDA+∠DAG＝90°．又∵∠EAB+∠DAG＝90°，∴∠FDA＝∠EAB．在△DAF与△ABE中，DA＝AB，∠FDA＝∠EAB，∠DAF＝∠ABE＝90°∴Rt△DAF≌Rt△ABE．∴AF＝BE．∵AB＝BC，∴BF＝CE．自学自测试题分析：根据正方形的判定：对角线互相垂直平分且相等的四边形是正方形进行判断即可.详解：A选项不能，只能判定为矩形；B选项不能，只能判定为平行四边形；C选项能判定为正方形；D选项不能，只能判定为菱形．故选答案C．即学即练试题分析：过D作DN⊥AB于N，首先根据矩形的判定证明四边形CEDF是矩形，再根据角平分线的性质可得ED＝DF，进而根据有一组邻边相等的矩形是正方形可得结论．证明：过D作DN⊥AB于N.∵∠C＝90°，DE⊥BC，DF⊥AC，∴四边形CEDF是矩形，∵∠BAC、∠ABC的平分线相交于点D，DE⊥BC，DF⊥AC，DN⊥AB，∴DF＝DN，DE＝DN，∴DF＝DE.∴四边形CEDF是正方形．精讲点拨例1 试题分析：本题主要考查了正方形的性质和判定.由已知可证△AEN≌△BFE≌△CMF≌△DNM，得四边形EFMN是菱形，再证有一个角是直角即可．详解：四边形EFMN是正方形．证明：在正方形ABCD中，AB=BC=CD=DA，∠A＝∠B＝∠C＝∠D＝90°.∵AE＝BF＝CM＝DN，∴AN＝DM＝CF＝BE．∵∠A＝∠B＝∠C＝∠D＝90°，∴△AEN≌△DMN≌△CFM≌△BEF．∴EF＝EN＝NM＝MF，∠ENA＝∠DMN．∴四边形EFMN是菱形．∵∠ENA＝∠DMN，∠DMN+∠DNM＝90°，∴∠ENA+∠DNM＝90°．∴∠ENM＝90°．∴四边形EFMN是正方形．例2试题分析：根据正方形的性质证出△COH≌△BOE，得到OE＝OH，同理可证OE＝OF＝OG，根据等式性质得到EG＝FH，又因为EG⊥FH，所以四边形EFGH为正方形．证明：∵四边形ABCD为正方形，∴OB＝OC，∠ABO＝∠BCO＝45°，∠BOC＝90°＝∠2+∠3．∵EG⊥FH，∴∠1+∠3＝90°．∴∠1＝∠2．∴△COH≌△BOE．∴OE＝OH．同理可证：OE＝OF＝OG．∴OE+OG＝OF+OH，即EG＝FH．又∵EG⊥FH，∴四边形EFGH为正方形．变式训练试题分析：本题考查了正方形的判定和性质，解题的关键是正确的利用正方形的性质．（1）根据正方形的性质判定△ADE≌△ABF后即可得到BF＝DE；（2）利用正方形的判定方法判定四边形AFBE为正方形即可．（1）证明：在正方形ABCD中，AB＝AD，∠BAD＝90°.∵AF⊥AC，∴∠EAF＝90°，∴∠BAF＝∠EAD，在△ADE和△ABF中∴△ADE≌△ABF（SAS），∴BF＝DE.（2）解：当点E运动到AC的中点时四边形AFBE是正方形，理由：∵点E运动到AC的中点，AB＝BC，∴BE⊥AC，BE＝AE＝AC，∵AF＝AE，∴BE＝AF＝AE.又∵BE⊥AC，∠FAE＝∠BEC＝90°，∴BE∥AF，∵BE＝AF，∴四边形AFBE是平行四边形.∵∠FAE＝90°，AF＝AE，∴四边形AFBE是正方形．星级达标：1.试题分析：根据正方形的判定定理判断即可．详解：A选项四个角都相等的四边形是矩形，故错误；B选项四条边都相等的四边形是菱形，故错误；C选项对角线相等的平行四边形是矩形，故错误；D选项对角线互相垂直的矩形是正方形，正确，故选答案D．2.试题分析：根据矩形、菱形、正方形的判定方法逐个判断即可．详解：A选项∵四边形ABCD是平行四边形，又∵AB＝BC，∴四边形ABCD是菱形，故本选项不符合题意；B选项∵四边形ABCD是平行四边形，又∵AC⊥BD，∴四边形ABCD是菱形，故本选项不符合题意；C选项∵四边形ABCD是平行四边形，又∵∠ABC＝90°，∴四边形ABCD是矩形，故本选项符合题意；D选项∵四边形ABCD是平行四边形，又∵AC＝BD，∴四边形ABCD是矩形，又不一定是正方形，故本选项不符合题意；故选答案C．3.试题分析：由四边形ABCD中，∠ABC＝∠BCD＝∠CDA＝90°，可得四边形ABCD是矩形，即可得当AB＝BC或AC⊥BD时，四边形ABCD是正方形．详解：∵四边形ABCD中，∠ABC＝∠BCD＝∠CDA＝90°，∴四边形ABCD是矩形，∴当AB＝BC或AC⊥BD时，四边形ABCD是正方形．故答案为：AB＝BC或AC⊥BD．4.试题分析：要判定是正方形，则需能判定它既是菱形又是矩形．详解：有6种选法：（1）①②：由①得有一组邻边相等的平行四边形是菱形，由②得有一个角是直角的平行四边形是矩形，所以平行四边形ABCD是正方形，正确；（2）②③：由②得有一个角是直角的平行四边形是矩形，由③得对角线相等的平行四边形是矩形，所以不能得出平行四边形ABCD是正方形，错误；（3）①③：由①得有一组邻边相等的平行四边形是菱形，由③得对角线相等的平行四边形是矩形，所以平行四边形ABCD是正方形，正确；（4）②④：由②得有一个角是直角的平行四边形是矩形，由④得对角线互相垂直的平行四边形是菱形，所以平行四边形ABCD是正方形，正确；（5）①④：由①得有一组邻边相等的平行四边形是菱形，由④得对角线互相垂直的平行四边形是菱形，所以不能得出平行四边形ABCD是正方形，错误；（6）③④：由③得对角线相等的平行四边形是矩形，由④得对角线互相垂直的平行四边形是菱形，所以平行四边形ABCD是正方形，正确.综上所述：错误的是：②③或①④；故答案为：②③或①④．5．试题分析：（1）根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD，由全等三角形的性质即可得到：∠ADB＝∠CDB；（2）若∠ADC＝90°，由（1）中的条件可得四边形MPND是矩形，再根据邻边相等的矩形是正方形即可证明四边形MPND是正方形．证明：（1）∵对角线BD平分∠ABC，∴∠ABD＝∠CBD.在△ABD和△CBD中，，∴△ABD≌△CBD（SAS）.∴∠ADB＝∠CDB.（2）∵PM⊥AD，PN⊥CD，∴∠PMD＝∠PND＝90°.∵∠ADC＝90°，∴四边形MPND是矩形.∵∠ADB＝∠CDB，PM⊥AD，PN⊥CD，∴PM＝PN.∴矩形MPND是正方形．6.试题分析：（1）由正方形的性质得到∠B＝∠ADC＝∠BCD＝90°，BC＝CD，根据全等三角形的判定和性质即可得到结论；（2）根据已知条件得到四边形CEGF是平行四边形，根据全等三角形的性质得到CE＝CF，证得四边形CEGF是菱形，求得∠ECF＝∠BCD＝90°，于是得到结论．（1）证明：∵四边形ABCD是正方形，∴∠B＝∠ADC＝∠BCD＝90°，BC＝CD，∴∠B＝∠CDF＝90°，在△BCE与△DCF中，∴△BCE≌△DCF（SAS），∴∠BCE＝∠DCF.（2）解：四边形CEGF是正方形. 理由：∵EG∥CF，FG∥CE，∴四边形CEGF是平行四边形.∵△BCE≌△DCF，∴CE＝CF.∴四边形CEGF是菱形.∵∠BCE＝∠DCF，F 6题图EDCBAG∴∠ECF＝∠BCD＝90°. ∴四边形CEGF是正方形．。

正方形的判定导学案学习目标：经历探索正方形判定的过程，掌握正方形的判定方法，理解正方形与平行四边形、矩形、菱形之间的联系，能够灵活地证明正方形.学习过程：一、复习回顾1、正方形的定义①②2、正方形的性质二、引入新知三、探究新知——正方形的判定方法1、探究一：什么样的矩形是正方形？小结：的矩形是正方形；练习：如图，在矩形ABCD中，对角线AC与BD相交于点O．若不增加任何字母与辅助线，要使得四边形ABCD是正方形，则还需增加的一个条件是 .2、探究二：什么样的菱形是正方形？小结：的菱形是正方形.练习：如图所示，菱形ABCD中，对角线AC，BD相交于点O，若再补充一个条件能使菱形ABCD成为正方形，则这个条件是 .3、总结正方形的判定方法四、巩固新知例1.下列说法不正确的是（）A. 有一个角是直角的菱形是正方形B. 两条对角线相等的菱形是正方形C. 对角线互相垂直的矩形是正方形D. 四条边都相等的四边形是正方形例2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )A. CD=,AC=,∥ABCDABBDB.C.D.例3.如下图所示，在Rt △ABC 中，∠ACB ＝90°，CD 是∠ACB 的平分线，DE ⊥BC ，DF ⊥AC ，垂足分别是E 、F.求证：四边形CFDE 是正方形.五、能力拓展在△ABC 中，AD 是BC 边上的中线，E 是AD 的中点，过点A 作AF ∥BC ，交BE 的延长线于点F ，连结CF.（1）求证：① △AEF ≌△DEB ；② 四边形ADCF 是平行四边形； （2）若AB=AC ，∠BAC=90°，试判断四边形ADCF 的形状，并证明你的结论.六、课堂小结七、作业《课堂同步练习册》P65-66BD AC DO CO BO AO ⊥===,BC AB DO BO CO AO ===,,BCD BAD BC AD ∠=∠,∥ B DC E A F。

北师大版九年级数学上册第一章 1.3.2正方形的判定 导学案预习目标1．掌握正方形的判定定理，并能综合运用特殊四边形的性质和判定解决问题．2．发现决定中点四边形形状的因素，熟练运用特殊四边形的判定及性质对中点四边形进行判断．预习导学阅读教材P22～24，完成下列问题：(一)知识探究1．对角线相等的________是正方形．2．对角线垂直的________是正方形．3．有一个是直角的________是正方形．(二)自学反馈1．已知四边形ABCD 中，∠A ＝∠B ＝∠C ＝90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是( )A ．∠D ＝90°B ．AB ＝CDC ．AD ＝BC D ．BC ＝CD2．下列命题正确的是( )A ．两条对角线相等的菱形是正方形B ．对角线与一边的夹角是45°的四边形是正方形C ．两邻角相等，且有一角是直角的四边形是正方形D ．对角线相等且互相垂直的四边形是正方形3．在四边形ABCD 中，O 是对角线的交点，能判定这个四边形是正方形的条件是( )A ．AC ＝BD ，AB ∥CD ，AB ＝CDB ．AD ∥BC ，∠A ＝∠CC ．AO ＝BO ＝CO ＝DO ，AC ⊥BDD ．AO ＝CO ，BO ＝DO ，AB ＝BC4．如图，将一张矩形纸片ABCD 折叠，使AB 落在AD 边上，然后打开，折痕为AE ，顶点B 的落点为F.则四边形ABEF 是________形．例题讲解活动1 小组讨论例 如图，在矩形ABCD 中，BE 平分∠ABC ，CE 平分∠DCB ，BF ∥CE ，CF ∥BE.求证：四边形BECF 是正方形．证明：∵BF ∥CE ，CF ∥BE ，∴四边形BECF 是平行四边形．∵四边形ABCD 是矩形，∴∠ABC ＝90°，∠DCB ＝90°.又∵BE 平分∠ABC ，CE 平分∠DCB ，∴∠EBC ＝12∠ABC ＝45°，∠ECB ＝12∠DCB ＝45°. ∴∠EBC ＝∠ECB.∴EB ＝EC.∴平行四边形BECF是菱形．在△EBC中，∵∠EBC＝45°，∠ECB＝45°，∴∠BEC＝90°.∴菱形BECF是正方形．提示：掌握平行四边形、矩形、菱形成为正方形所需要的条件是解决这类问题的关键．活动2 跟踪训练1．如图，在△ABC中，∠ABC＝90°，BD平分∠ABC，DE⊥BC，DF⊥AB，垂足分别为E、F，求证：四边形BEDF是正方形．2．如图，E、F、G、H分别是正方形ABCD四条边上的点，AE＝BF＝CG＝DH，四边形EFGH是什么图形？证明你的结论．3．如图所示，点E，F，G，H分别是CD，BC，AB，DA的中点，求证：四边形EFGH是平行四边形．活动3 课堂小结1．对角线相等的菱形是正方形；2．对角线垂直的矩形是正方形；3．有一个角是直角的菱形是正方形．参考答案【预习导学】(一)知识探究1．菱形 2.矩形 3.菱形(二)自学反馈1．D 2.A 3.C 4.正方【合作探究】活动2跟踪训练1．证明：∵∠ABC＝90°，DE⊥BC，DF⊥AB，∴四边形BEDF是矩形．∵BD平分∠ABC，DE⊥BC，DF⊥AB，∴DE＝DF.∴四边形BEDF是正方形．2．四边形EFGH 是正方形．证明：∵四边形ABCD 是正方形，∴AB ＝BC ＝CD ＝DA.∵AE ＝BF ＝CG ＝DH ，∴HA ＝EB ＝FC ＝GD.∵∠A ＝∠B ＝∠C ＝∠D ＝90°，∴Rt △AEH ≌Rt △BFE ≌Rt △CGF ≌Rt △DHG.∴HE ＝EF ＝FG ＝GH.∴四边形EFGH 是菱形．又∠AHE ＝∠BEF ，∠AHE ＋∠AEH ＝90°，∴∠BEF ＋∠AEH ＝90°.∴∠HEF ＝90°.∴四边形EFGH 是正方形．3．证明：连接BD.∵点E ，F ，G ，H 分别是CD ，BC ，AB ，DA 的中点，∴EF 是△BCD 的中位线，GH 是△ABD 的中位线．∴EF ∥BD ，EF ＝12BD ，GH ∥BD ，GH ＝12BD.∴EF ∥GH ，EF ＝GH.∴四边形EFGH 是平行四边形．。

19.3正方形的判定导学案【学习目标】1. 掌握正方形的判定并会用它们进行有关的论证和计算。

2. 理解正方形与平行四边形、矩形、菱形的联系和区别。

学习重点：正方形性质的灵活运用。

学习难点：正方形与矩形、菱形的关系。

一、自主学习：复习回顾：1.平行四边形的判定方法：1）2）3）4）2.矩形的判定方法：1）2）3）3.菱形的判定方法：1）2）3）4.正方形的性质：是最特殊的平行四边形，既是矩形，又是；具体为：①边：四边，对边；②角：四个角都是；③对角线：互相、且。

5.正方形图形的特殊性：既是中心对称图形，又是轴对称图形，有条对称轴。

（一）先自己回忆（二）小组内相互说一说结果（三）挑几个同学回答（四）老师点评二、合作探究1、探讨1. 你能否利用手中的矩形白纸裁出一个正方形呢？然后与同小组同学交流一下，说说矩形与正方形的关系。

归纳：（1）矩形+（）=正方形；即正方形的判定定理（一）探讨2. 你能否利用手中的可以活动的菱形模型变成一个正方形吗？如何变？归纳：（1）菱形+（）=正方形；即正方形的判定定理（二）小结：正方形的判定方法：①定义：有一组相等并且有一个角是的叫做正方形.②正方形的判定定理（一）：的矩形是正方形。

③正方形的判定定理（二）：的菱形是正方形。

2、课本120页讨论。

3、如图，在ABC中∠ACB=90°，CD平分∠ACB，DE⊥BC，DF⊥AC,垂足分别为E、F，求证：四边形CFDE为正方形（一）独立完成上面各题（二）组内对答案，解决问题（三）挑学生展讲（四）教师总结正方形的两种判定方法三、归纳整理：1、正方形与平行四边形、矩形、菱形、正方形的联系？2、正方形的两种判定方法？四、分层训练：1.下列说法是否正确，并说明理由．① 有一个角为直角的菱形是正方形；（）② 四个角相等的四边形是正方形．（）③ 四条边都相等的四边形是正方形；（）④ 有一组邻边相等的矩形是正方形；（）⑤ 对角线垂直且相等的四边形是正方形（）⑥ 对角线相等的菱形是正方形；（）⑦ 对角线互相垂直的矩形是正方形；（）⑧ 对角线互相垂直平分的四边形是正方形；（）2. 四边形ABCD中，AC、BD相交于点O，能判别这个四边形是正方形的条件是（）A.OA=OB=OC=OD，AC⊥BDB.AB∥CD，AC=BDC.AD∥BC，∠A=∠CD.OA=OC，OB=OD，AB=BC3.下列命题中的假命题是( )．A．一组邻边相等的平行四边形是菱形B. 一组对边平行且相等的四边形是平行四边形C．一组邻边相等的矩形是正方形D．一组对边相等且有一个角是直角的四边形是矩形4. 顺次连结矩形的各边中点，所得的四边形一定是（）Ａ．正方形Ｂ．菱形Ｃ．矩形Ｄ．梯形5、拓展提升：已知:矩形ABCD,它的四个角平分线交于E,F,G,H.求证:四边形EFGH是正方形（一）独立完成（二）组内对答案并解决问题（三）利用白板展讲（四）老师点评证明方法，并纠错。

18.2.3第2课时正方形的判定导学案一、知识点概述本课时主要介绍如何通过四个点的坐标判断它们能否组成一个正方形，并对如何利用正方形的性质解决实际问题进行讲解。

二、教学目标1.能够根据四个点的坐标判断它们能否组成一个正方形。

2.能够理解正方形的定义及性质。

3.能够灵活应用正方形的性质解决实际问题。

三、教学重点1.正方形的定义及性质。

2.通过四个点的坐标判断它们能否组成一个正方形。

四、教学难点1.如何通过四个点的坐标判断它们能否组成一个正方形。

2.如何利用正方形的性质解决实际问题。

五、教学内容及进度安排序号知识点课时知识点讲解案例演示习题讲解1正方形的定义及性质1课时通过幂等律、对称律和传递律讲解正方形的性质无无2通过四个点的坐标判断它们能否组成一个正方形1课时讲解如何计算每条边的长度和对角线的长度，并根据判断条件判断是否为正方形2个案例3个习题六、教学方法1.讲授法：通过点拨学生的疑点，讲解正方形的定义及性质。

2.实例法：通过具体的案例演示，让学生更好地理解正方形的性质及判定方法，增强学生对相关知识点的记忆和理解。

3.互动式教学法：通过讲解习题解法，增强学生对知识的运用和实践能力，提高学生的解题技巧。

七、教学手段1.教具：黑板、白板、笔、化学试剂，图形计算器等。

2.多媒体教学手段：使用幻灯片、视频、网站等多媒体教学手段辅助课堂教学，提高教学效果。

八、教学反思本课时主要介绍了正方形的定义及性质，以及如何通过四个点的坐标判断它们能否组成一个正方形，并对如何利用正方形的性质解决实际问题进行了讲解。

通过互动式教学法，讲解多个案例，让学生理解更为深入，对于提高学生的解题技巧有一定帮助。

在教学中，需要注意加强对学生的思维启发，帮助学生形成自己的解题思路。