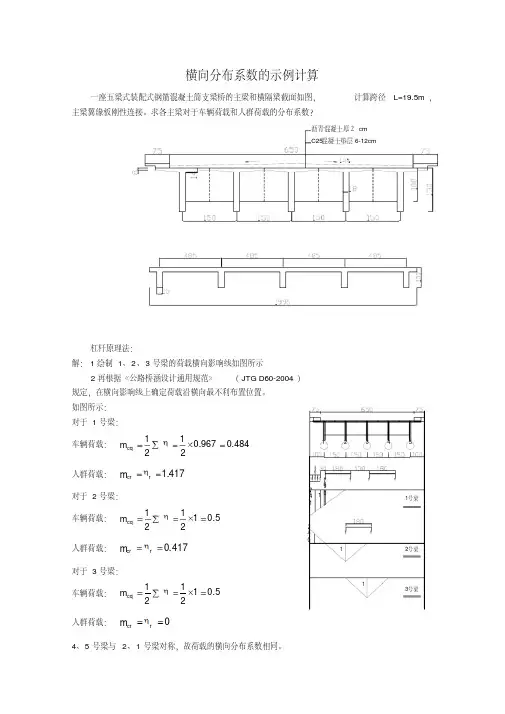
横向影响线竖坐标值偏心压力法横向影响线竖坐标值偏心压力法是一种计算结构内力和变形的方法。
它适用于桥梁、房屋等结构的静力分析和设计。
本文将详细介绍横向影响线竖坐标值偏心压力法的原理、计算步骤、应用范围以及注意事项。
一、原理横向影响线竖坐标值偏心压力法是基于静平衡原理和受力平衡原理，通过建立受力模型，求解结构内部受力和变形的方法。
具体来说，该方法将结构分为若干个截面，在每个截面上分别考虑受力平衡和变形条件，得出各个截面上的内力和变形。
其中，横向影响线指的是荷载作用下结构中各点的位移量。
二、计算步骤1. 建立受力模型：根据实际情况选择合适的受力模型，如简支梁、连续梁等。
2. 确定荷载：根据设计要求确定荷载类型、大小及作用位置。
3. 划分截面：将结构按照一定间隔划分为若干个截面，每个截面上都要考虑受力和变形条件。
4. 建立影响线：根据荷载作用下结构的位移量，建立影响线，即各点的位移量与荷载大小的比值。
5. 计算竖向偏心距：根据结构几何形状和荷载作用位置计算出各截面上的竖向偏心距。
6. 计算偏心压力：根据竖向偏心距和影响线计算出各截面上的偏心压力。
7. 计算内力：根据受力平衡原理，在每个截面上计算出正、剪、弯矩等内力。
8. 计算变形：根据变形条件，在每个截面上计算出位移、角度等变形量。
9. 检验结果：检验计算结果是否符合设计要求，如内力大小是否满足强度、刚度等要求。
三、应用范围横向影响线竖坐标值偏心压力法适用于桥梁、房屋等结构的静力分析和设计。
特别适用于连续梁桥等大跨度桥梁的分析与设计。
在实际应用中，需要根据具体情况选择合适的受力模型和荷载类型，以及合理的截面划分间距。
四、注意事项1. 建立受力模型时需要考虑结构的实际情况，如支座类型、梁端条件等。
2. 划分截面时需要考虑结构的几何形状和荷载作用位置，以及内力变化的规律。
3. 影响线建立时需要根据荷载大小和作用位置确定各点的位移量。
4. 计算偏心压力时需要考虑竖向偏心距和影响线的相互作用关系。
