当前位置：文档之家 › 2016D1JB2荷载横向分布计算(刚性横梁法)(模板)

2016D1JB2荷载横向分布计算(刚性横梁法)(模板)

  • 格式：doc
  • 大小：316.50 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

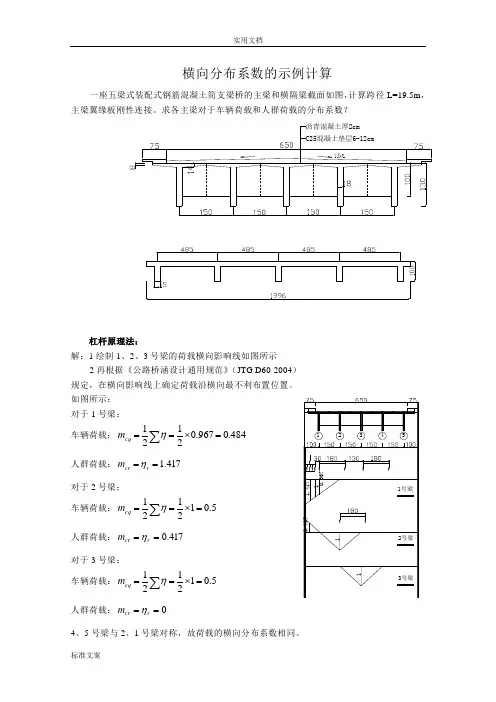
横向分布系数计算(多种方法计算)

横向分布系数计算(多种方法计算)

实用文档标准文案横向分布系数的示例计算一座五梁式装配式钢筋混凝土简支梁桥的主梁和横隔梁截面如图，计算跨径L=19.5m ，主梁翼缘板刚性连接。

求各主梁对于车辆荷载和人群荷载的分布系数？杠杆原理法：解：1绘制1、2、3号梁的荷载横向影响线如图所示2再根据《公路桥涵设计通用规范》（JTG D60-2004） 规定，在横向影响线上确定荷载沿横向最不利布置位置。

如图所示： 对于1号梁： 车辆荷载：484.0967.02121=⨯==∑ηcq m 人群荷载：417.1==r cr m η 对于2号梁： 车辆荷载：5.012121=⨯==∑ηcq m 人群荷载：417.0==r cr m η 对于3号梁： 车辆荷载：5.012121=⨯==∑ηcq m 人群荷载：0==r cr m η4、5号梁与2、1号梁对称，故荷载的横向分布系数相同。

偏心压力法（一）假设：荷载位于1号梁 1长宽比为26.25.155.19>=⨯=b l ，故可按偏心压力法来绘制横向影响线并计算横向分布系数c m 。

本桥的各根主梁的横截面积均相等，梁数为5，梁的间距为1.5m ，则：5.220)5.11(2)5.12(2222524232221512=+⨯+⨯=++++=∑=a a a a a ai i2所以1号5号梁的影响线竖标值为：6.0122111=+=∑i a a n η 2.0122115-=-=∑i a a n η由11η和15η绘制荷载作用在1号梁上的影响线如上图所示，图中根据《公路桥涵设计通用规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。

进而由11η和15η绘制的影响线计算0点得位置，设0点距离1号梁的距离为x ，则：4502.015046.0=⇒-⨯=x xx 0点已知，可求各类荷载相应于各个荷载位置的横向影响线竖标值3计算荷载的横向分布系数 车辆荷载：()533.0060.0180.0353.0593.02121=-++⨯==∑ηcq m 人群荷载：683.0==r cr m η （二）当荷载位于2号梁时 与荷载作用在1号梁的区别以下：4.0122112=+=∑i a a a n η实用文档标准文案0122552=-=∑ia a a n η 其他步骤同荷载作用在1号梁时的计算修正偏心压力法（一）假设：荷载位于1号梁 1计算I 和T I ：2.3813018)2814(150)18150()2814(1301821)(2122221=⨯++⨯-+++⨯⨯=+-++⨯=ch bd c b d ch y8.912.3813012=-=-=y y y[][]43333313132106543)112.38)(18150(2.381508.911831))((31cm d y c b by cy I ⨯=---⨯+⨯⨯=---+⨯=对于翼板1.0073.01501111<==b t ，对于梁肋151.01191822==b t 查下表得所以：311=c ，301.02=c 433331027518119301.01115031cm t b c I i i i T ⨯=⨯⨯+⨯⨯==∑2计算抗扭修正系数β 与主梁根数有关的系数ε则n=5，ε=1.042 G=0.425E875.055.15.1910654310275425.0042.111)(112332=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯+=+=E E B l EI GI T εβ 3计算荷载横向影响线竖标值11η和15η55.0122111=+=∑i a a n βη 15.0122115-=-=∑ia a n βη 由11η和15η绘制荷载作用在1号梁上的影响线如上图所示，图中根据《公路桥涵设计通用规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。

2020D1JB2荷载横向分布计算(刚性横梁法)(模板)

2020D1JB2荷载横向分布计算(刚性横梁法)(模板)

第三章 荷载横向分布计算由于本桥各T 梁之间采用混凝与湿接缝刚性连接，故其荷载横向分布系数，在梁端可按“杠杆原理法”计算（m 0），在跨中按“修正刚性横梁法”计算(m c )。

（一）梁端的横向分布系数m 0根据桥规规定，在横向影响线确定荷载沿横向最不利的布置位置。

例如，对于汽车荷载，规定的汽车横向轮距为1.8m ，两列汽车车轮的横向最小间距为1.30m,车轮距离人行道缘石最少为0.50m 。

求出相应于荷载位置的影响线竖标值后，就可得到横向所有荷载分布给1号梁的最大荷载值为： 式子中：q P —汽车荷载轴重；q η—汽车车轮的影响线竖标。

由此可得：1号梁在汽车荷载作用下最不利荷载横向分布系数为654.001=m 同理有：904.002=m ；904.003=m ；904.004=m ；904.005=m ；654.006=m（二）跨中的横向分布系数m c 1.计算I 和I T求主梁截面中心位置a x (距梁顶)翼板的换算平均厚度 cm h 19224141=+=马蹄形下翼缘换算厚度 cm h 5.34228412=+=S ≈ (260-18)×19×19/2+245×18×245/2=583906cm 3 A ≈(260-18)×19+245×18=9008cm 2 重心距离 a x =S/A=583906/9008=64.82cm 主梁抗弯惯性矩：I ≈1/12×(260-18)×193+(260-18)×19×(64.82-19/2)2+1/12×18×2453 +18×245×(245/2-64.82)2=cm 4=0.5094m 4 翼板主梁抗扭惯性矩b 1/t 1=260/19=13.68＞10, 查表得c 1=0.33梁肋b 2=245-19=226cmb 2/t 2=226/18=12.6＞10, 查表得c 2=0.33 I T =∑c i b i t i 3=0.33×260×193+0.33×226×183=1023452cm 4=0.0102m 42.计算抗扭修正系数β本桥各主梁的横截面均相等，梁数n=6，梁间距为2.6m ，则 其中：E —混凝土弹性模量；G —混凝土剪切模量，E G 43.0=。

荷载横向分布系数的计算 杠杆法

荷载横向分布系数的计算 杠杆法
（2）在梁桥空间结构的近似计算中，“荷载横向分布”仅是借用 的一个概念，实质是“内力”横向分布。只是在变量分离后在计 算式的表现上成了“荷载”横向分布。
（3）严格地说，任意位置（x,y）上的各个内力S（x,y） 都有各自 的内力影响面，在实用计算方法中，应有各自的荷载横向分布系 数。实际上，主梁各截面弯矩的横向分布系数均采用全跨单一的 跨中截面横向分布系数，但剪力必须考虑横向分布系数的变化。
是两个支承反力之和。
✓ 根据主梁的荷载横向影响线、活载的最不利布置计算横向分布
系数 moq和mor。 注：采用此法时，应计算各根主梁的横向分布系数，以得到受载 最大的主梁的最大内力作为设计依据。
二、杠杆原理法
➢ 假定荷载横向分布影响线的
坐标为η ，车辆荷载轴重为
Pq ，轮重为 Pq/2，按最不
利情况布载，则分布到某主
第二篇 混凝土梁桥
第二章 简支梁桥的计算
第一节 第二节 第三节 第四节 第五节 第六节
行车道板的计算 荷载横向分布计算 主梁内力计算 横隔梁内力计算 挠度、预拱度的计算 配筋的计算
第二节 荷载横向分布计算
）
（
（ ）
（ ）
a
b
1 . 8 1 . 3 1 1..88 1 . 3 1 . 8
）
（
c
d
）
一、概述
➢ 荷载横向分布计算方法：由于施工特点、构造设计等的不同——采用不
同类型的横向结构——不同的简化计算模型 ✓ 杠杆原理法：把横向结构（桥面板和横隔梁）看作在主梁上断开而简 支在其上的简支梁和悬臂梁
✓ 偏心压力法：把横隔梁看作刚性极大的梁；当计及主梁抗扭刚度影响 时，此法又称为修正偏心压力法
P
y

荷载横向分布系数的计算杠杆法

荷载横向分布系数的计算杠杆法

(
y
)
：单位荷载沿横向作用在不同位置时，对某梁所分配旳荷载 比值变化曲线，也称为对于某梁旳荷载横向分布影响线。
一、概述
P3 P3 22
P2 P2 22 P1 P1 22
x
m3 P3
m1P1
m2 P2 K
问题？
计算 3 号梁 k 点截面内力。
123 45
y
3
S P 2(y)1 (x) P'1(x) P' P 2 ( y)
1
160
2
160
3
160
4
160
5
105
表 各根主梁旳荷载横向分布系数
梁号
m0q
m0r
1、5号梁
0.438
1.422
2、4号梁
0.5
0
3号梁
0.594
0
二、杠杆原理法 The End
疑问？
（1）把空间问题转化为平面问题：近似处理措施。近似处理旳实质是什 么？
实质：在一定旳误差范围内，谋求一种近似旳内力影响面替代精 确旳内力影响面。
的荷载横向影响线坐标。
1
2号梁
图 杠杆原理法计算横向分布系数
假定荷载横向分布影响线旳坐 标为η ，车辆荷载轴重为 Pq ，轮重为 Pq/2，按最不利情 况布载，则分布到某主梁旳最 大荷载为：
则P'汽max车荷载P2横向 分(布12 系数 )为 P：
人群荷载横向分布系数为：
1
m0q 2
q
m0r r
一、概述
梁桥由承重构造（主梁）及传力构造（横梁、桥面板）两大部分构成。多 片主梁依托横梁和桥面板连成空间整体构造。 主梁内力：与桥梁横截面形式、荷载类型、荷载作用位置有关。 精确旳空间构造分析措施：有限元理论

荷载横向分布计算详细总结(全)

荷载横向分布计算详细总结(全)
⑥ 和 分别作用在1号边梁和 号边梁上时，各片梁的荷载横向分布系数调整值为：
将式(a)与式(b)相加后，与式7-2联立，可得如下方程组：
= 式(7-2)
(式7-2)的具体推导过程见下图：
图6.6
⑦解上述方程组，解得：
(式7-3)
—第 片主梁的抗扭惯性矩。
G—材料的剪切模量，对于混凝土结构，G=0.425E。
注：修正偏心压力法作出的荷载横向分布影响线是一条直线。
5.铰接板（梁）法：（①中梁和边梁抗弯刚度相等或者接近②跨中）
☆适用条件：现浇砼纵向企口缝连结的装配式桥、仅在翼板间用钢板或钢筋连接的无中间横隔梁的装配式T梁桥。此类桥横向有一定连结构造，但刚性弱，板（梁）之间的连接可以看成是铰接。
矩阵B是 阶三对角方阵，其组成规律为：主对角线上的元素均为 ，剩余两条对角线元素均为 。
矩阵C为 阶方阵，组成规律为：主对角线上元素均为0，主对角线上侧第一条对角线上元素均为 ，主对角线下册第一条对角线上元素均为 （可以将矩阵C看成是一个主对角线元素为0的特殊三对角矩阵）。具有n片主梁时，矩阵C的一般形式见下图6.2：
注：铰接板（梁）法作出的荷载横向分布影响线是一条光滑曲线。
6.刚接板（梁）法：（①中梁和边梁抗弯刚度相等或者接近；②跨中）
☆适用条件：各种桥面板刚接的肋梁桥。对于整体式板桥，使用刚接梁法计算时，把整体式板划分成 块等宽度 的板（一般 ），当做彼此之间刚接的板桥来计算其荷载的横向分布。需要注意的是，将整体式板划分成 块等宽度为 的板时，每一块板的宽跨比 不宜大于1/4。
其中： —每片主梁的抗弯惯性矩。
—每片主梁的抗扭惯性矩。
—单位宽度翼缘板的抗弯惯性矩。
—梁（板）截面宽度。
—翼缘板的悬出长度。

刚性横梁法及主梁计算第2篇解析

刚性横梁法及主梁计算第2篇解析

绘制1号梁横向影响线确定汽车荷载的最不利位置
设零点至1号梁位的距离为x
解得x=4.80m 设人行道缘石至1号梁轴线的距离为△
1号梁的活载横向分布系数可计算如下: 汽车荷载
人群荷载
• 三、荷载横向分布的计算
2、荷载横向分布系数的计算方法 （3）荷载横向分布计算的其他方法简介
① 修正的刚性横梁法 ② 铰结板（梁）法 ③ 刚结板（梁）法 ④ 比拟正交异性板法
n
Ii
i1
ai Iie
n i1
ai2 I i
当各主梁截面相同时：
Ri
P(1 n
eai
n
)
ai2
i 1
三、荷载横向分布的计算
2、荷载横向分布系数的计算方法 （2）刚性横梁法
② 利用荷载横向分布影响线求主梁的m
令P=1依次变化e，则可求出第i根主梁荷载横 向分布影响线纵标η。
i
(1 n
eai
n
简支梁桥的计算二
一、刚性横梁法 二、主梁内力计算
三、荷载横向分布的计算
2、荷载横向分布系数的计算方法 （2）刚性横梁法（偏心受压法）
假定 ①横梁是刚性的：宽跨比B/l≤0.5
②忽略主梁抗扭刚度
① 偏心荷载P作用下各主梁所分担 的荷载 从图中可以看出，在上述前提假定 下，桥面在偏心荷载作用下的变形 为一直线，且靠近活载一侧的边梁 受载最大
• 每IITTyx根。，主横梁隔的梁截的面截抗面弯抗惯弯矩惯和矩抗和扭抗惯扭矩惯分矩别分为别I为x、Iy、 • 比上拟，正Iy和交I异Ty性均板匀法分就摊是于把a上Ix。和得ITx到均了匀在分x摊、于y方b宽向度
截GJ面Ty的单正宽交抗异弯性刚板度，EJ求x、解E在Jy单和位抗扭荷刚载度下G的J板Tx、挠度 曲线，据荷载与挠度关系求各根主梁处荷载横向 分布影响线。

荷载横向分布的计算

荷载横向分布的计算

三、荷载横向分布的计算
2、荷载横向分布系数的计算方法 常用的计算方法： ◆ 杠杆原理法 ◆ 刚性横梁法 ◆ 修正的刚性横正交异性板法（G-M法） 从分析荷载在桥上的横向分布出发，求得各梁 的荷载横向分布影响线，再通过横向最不利加载来 计算荷载横向分布系数
多主梁桥的内力计算
S P ( x, y) P 2 ( y) 1 ( x)
三、荷载横向分布的计算
1、荷载横向分布系数的概念
荷载横向分布系数表示某根主梁所承担的最大荷载与轴 重的比值
车轮荷载的横向分布
三、荷载横向分布的计算
1、荷载横向分布系数的概念 荷载横向分布系数与各主梁之间的横向联系有直 接关系。
三、荷载横向分布的计算
2、荷载横向分布系数的计算方法 荷载横向分布影响线：P=1在梁上横向移动时，某 主梁所相应分配到的不同的荷载作用力。 对荷载横向分布影响线进行最不利加载Pi，可 求得某主梁可行最大荷载力

荷载横向分布系数：将Pi除以车辆轴重。
三、荷载横向分布的计算
2、荷载横向分布系数的计算方法 （1）杠杆分配法
二、行车道板的计算
1、车辆活载在板上的分布 公路汽车荷载

轮压一般作为分布荷载处理 车轮着地面积：a1×b1
桥面板荷载压力面：a2×b2
荷载在铺装层内按45°扩散 沿纵向：a2＝a1 +2h


沿横向：b2=b1+2h
桥面板的轮压局部分布荷载：
公路桥面板上车轮荷载的扩散
P p 2a2b2
三、荷载横向分布的计算
1、荷载横向分布系数的概念 公路桥梁桥面较宽，主梁片数往往较多并与桥 面板和横隔梁联结在一起。当桥上车辆处于横向不 同位置时，各主梁参与受力的程度不同，属空间问 题，求解难度大。 应将空间问题简化为平面问题。

桥梁工程荷载横向分布计算简介

桥梁工程荷载横向分布计算简介
桥梁工程荷载横向分布计算简介
分析：荷载横向分布影响线竖标值与刚度参数γ ，板 块数n以及荷载作用位置有关。 5.8 I (b)2
IT l
抗弯I 惯 13矩 911 30cm 4 抗扭 IT 惯 2.3 7 矩 160 c4 m
桥梁工程荷载横向分布计算简介
采用查表法求荷载横向影响线竖标值（附录I）P404 (n=9, γ =0.0214)
公路－I级
桥梁工程荷载横向分布计算简介
七、横向分布系数沿桥纵向的变化
•对于弯矩
由于跨中截面车轮加载值占总荷载的绝大多数，近 似认为其它截面的横向分布系数与跨中相同
•对于剪力
从影响线看跨中与支点均占较大比例 从影响面看近似影响面与实际情况相差较大
桥梁工程荷载横向分布计算简介
荷载横向分布计算
桥梁工程荷载横向分布计算简介
一、概述
荷载：恒载：均布荷载（比重×截面积） 活载：荷载横向分布
1、活载作用下，梁式桥内力计算特点： （1）单梁 （平面问题）
S=P·η1（x）
P
x
L/4
1
桥梁工程荷载横向分布计算简介
（2）梁式板桥或由多片主梁组成的梁桥（空间问题）： S＝Ｐ·η（x，ｙ） 实际中广泛使用方法： 将空间问题转化成平面问题
先求翼板的有效作用宽度，由表2－5－4查得
c/l=235/(4x160)=0.368, λ/c=0.547 , λ=0.547x235=128cm
Iy＝3220x103cm4
主梁比拟单宽抗弯惯矩Jy＝Iy/a=3220x103cm4/485=6440 cm4/cm （3）主梁和横隔梁的抗扭惯矩
I`Tx= 208000cm4 ; I`Ty=88610cm4 因为主梁翼缘板刚性连接，所以按式（2－5－74）

荷载横向分布系数的计算

荷载横向分布系数的计算
荷载横向分布影响线为三角形
适用情况 ①只有邻近两根主梁参与受力 ②虽为多主梁，但计算梁端支承处荷载 ③无中间横隔梁
2、荷载横向分布系数的计算方法
（1）杠杆分配法
作业1：画 及出单3车、辆4荷号载梁作的用荷下载3横、向4分号布梁影荷响载线横，向
0.75m
分布系数 7m
0.75m
1
2 2m
3
4
（2）刚性横梁法（偏心受压法） 假定 ①横梁是刚性的：宽跨比B/l≤0.5 ②忽略主梁抗扭刚度
▪ 计算假设： ①铰式键只传递竖
向剪力 gx ；
②桥上荷载近似作为一个沿桥连续分布的正弦荷 载 P sin x，且作用于梁轴上。
l
求出各铰处gx， 即可求出横向分布影响线
1号板 2号板 3号板 4号板 5号板
p11 1 g1
p21 p31
g1 g2
g2 g3
p41
g3
g4
p51 g4
(1 )g3 2(1 )g4 0
半波正弦荷载引起的变形
w pl4
4EI
pbl 2
2 2GIT
b
2
/w
b 2
pbl 2
2 2GIT
pl4
4
EI
2EI
4GIT
b l
2
5.8
I IT
b l
2
③ 刚结板（梁）法
▪ 在铰结板（梁）计算理论的基础上，在结合 缝处补充引入冗余弯矩m，得到考虑板的横 向刚性连接特点的变形协调方程，从而求解 各梁荷载横向分布的方法。
P
ai Iie
n
ai2 Ii
i 1
P
P
Ii
n
Ii
i 1

刚性横梁法计算桥梁荷载横向分布系数

刚性横梁法计算桥梁荷载横向分布系数
刚性横梁法计算桥梁横向分布系数
关于荷载横向分布系数的一些结论：
1.梁桥实用空间理论的计算,实际上是应用荷载横向分布,将 空间问题转化为平面问题.
2.荷载横向分布,其实质是内力的横向分布. 3.严格地说,同一内力沿跨径方向在不同的截面横向分布系
数不同,不同内力在同一截面的横向分布系数也不同.在计 算中,主梁各截面弯矩的横向分布系数均采用全跨一的跨 中截面横向分布系数.但剪力必须考虑不同截面横向分布 系数的变化. 4.试验证明,按挠度、弯矩及主梁反力求得的横向分布系数 相差很小.报告结论中用实测挠度、应变求得的横向分布 系数来验证理论计算值.
Ri RiRi
Ii
n
P
Iiai
n
P（ e10）
Ii
Iiai2
i1
i1
式10是在不等间距不等刚度的结构中推导出来的,但大多数的梁
桥还是做成等间距等刚度的,从式10中很容易得到这种梁桥的主
梁荷载分配表达式：
Ri RiRi
P n
Pe
n
a（ i 11）
ai2
i1
图2-4-25表示等间距b1布置的主梁,刚度相等,用刚性横梁 连成整体.当P作用在左侧边梁,即e=2.5b1时,求分配给各片 主梁的荷载.
从力矩的平衡条件可知：
n
n
Ri ai ai2Ii Pe(8)
i1
i1
从式7得出
R
i
a iI i
将β代入式8得：
n
ai2Ii
i1
aiIi
Ri
Pe得Ri
PneaiI（ i 9） aiIi
i1
3.偏心荷载P对各梁产生的总的作用力,即各片主梁所分配 到的荷载,等于上述1和2两种情况的叠加,即：

刚性横梁法计算荷载横向分布系数的简化方法

刚性横梁法计算荷载横向分布系数的简化方法

第44卷第1期• 54 •2 0 1 8 年 1 月山西建筑SHANXI ARCHITECTUREVol. 44 No. 1 Jan. 2018文章编号：1009-6825 (2018) 01-0054-02刚性横梁法计算荷载横向分布系数的简化方法王扶义炱森 梁朝伟 朱健(陕西工业职业技术学院，陕西咸阳712000)摘要:利用刚性横梁法各个主梁横向分布影响线是直线的特点,提出了横向布载的判别公式，推导了刚性横梁法计算荷载横向 分布系数的简化计算公式,省略了绘制荷载横向分布影响线的步骤。

关键词：刚性横梁法,横向分布系数，简化计算中图分类号:TU 311.4文献标识码:A 刚性横梁法也称为偏心压力法，是计算多片式梁桥荷载横向 分布系数的常用方法，其基本假定是将横隔梁视作刚度极大的 梁，而且不考虑主梁的扭转影响，在车辆荷载作用下，仅发生刚性 变形而保持直线状态，各个主梁的荷载横向分布影响线是直线。

传统的计算方法是求得各个主梁的横向分布影响线及其值，然后 根据影响线布载，之后计算横向分布系数，本文利用横梁发生刚 性位移的特点，简化了计算过程并推导了相应的公式。

1计算主梁荷载横向分布系数的简化公式+——e_-----------+n ______________________________________P =l ^xM =l.e11〇 1 1图i偏心力作用图如图1所示，在某个偏心距为e 的偏心荷载P = 1作用下，其作用效果等效为一个中心力P = 1及一个偏心力矩M = P e 的作用SO -S 9-O-S 9-O-SSO -S 9-O-SSO -S 9-O-S 9-O-SSO -S 9-O-S 9-O-SSO -S 9-O-SSO -S 9-O-S 9-O-S工程影响较大，工期影响较大，优选形式1、形式2;平原地区施工 操作面较为开阔，各工程可依照合理的流程安排，保证同时施工， 优先选用经济性比较好的形式3。

刚性横梁法计算桥梁荷载横向分布系数

刚性横梁法计算桥梁荷载横向分布系数
未来可以研究更加精确的模型和算法，以提高计算精度和可靠性。
可以结合实际工程情况，对刚性横梁法进行改进和调整，以更好地满 足实际需求。
此外，还可以将刚性横梁法与其他数值分析方法进行比较和结合，以 实现优势互补，提高整体计算效果。
感谢观看
THANKS
优点
计算简单
刚性横梁法是一种简化的计算方 法，其计算过程相对简单，易于 理解和实现。
适用性强
该方法适用于多种类型的桥梁， 特别是主梁间距较小、横截面形 式一致的桥梁。
精度满足要求
对于许多实际工程，刚性横梁法 的计算精度已经足够满足需求， 能够提供较为准确的横向分布系 数。
缺点
1 2
假设限制
刚性横梁法基于一系列假设，如横梁的刚性、横 梁之间的无转角等，这些假设可能与实际情况存 在偏差。
刚度计算
根据桥梁的结构形式和材 料特性，通过计算或试验 确定横梁的弹性模量和截 面惯性矩。
刚度分类
根据刚度大小，可分为刚 性横梁和柔性横梁，刚性 横梁在受力时变形较小， 而柔性横梁则变形较大。
计算横向分布影响线
影响线定义
横向分布影响线是指在桥 梁上施加单位力时，各横 梁上反力分布的图形。
影响线计算
桥梁荷载横向分布系数的定义
01
桥梁荷载横向分布系数是指桥梁 承受的荷载在各横向分布位置的 分布情况，是衡量桥梁承载能力 和稳定性的重要指标。
02
横向分布系数的计算方法有多种 ，其中刚性横梁法是一种常用的 方法，适用于等跨径的桥梁。
02
刚性横梁法的基本原理
刚性横梁法的概念
刚性横梁法是一种计算桥梁荷载横向 分布系数的简化方法，基于刚性横梁 的假设，将多跨连续梁等效为一系列 独立的简支梁或固支梁。

桥梁荷载横向分布计算全过程解析(干货)

桥梁荷载横向分布计算全过程解析(干货)

桥梁荷载横向分布计算全过程解析（干货）
荷载横向分布计算原理
梁桥作用荷载P时，结构的刚性使P在x、y方向内同时传布，所有主梁都以不同程度参与工作。

可类似单梁计算内力影响线的方法，截面的内力值用内力影响面双值函数表示，即
荷载横向分布系数m
如果某梁的结构一定，轮重在桥上的位置也确定，则分布给某根梁的荷载也是定值。

在桥梁设计中，常用一个表征荷载分布程度的系数m与轴重的乘积来表示该定值。

m即为荷载横向分布系数，它表示某根梁所承担的最大荷载是各个轴重的倍数。

常用几种荷载横向分布计算方法
杠杆原理法
刚性横梁法
刚性横梁法横向分布系数计算图示
修正刚性横梁法。

第五节荷载横向分布计算

第五节荷载横向分布计算

一、杠杆原理法 ㈠按杠杆原理法进行荷载横向分布计算的基本假定:
是忽略主梁之间横向结构的联系作用，即假设桥面 板在主梁梁肋处断开，而当作沿横向支承在主梁上 的简支梁或悬臂梁来考虑，如图所示。
㈡杠杆原理法适用条件：
1、荷载位于靠近主梁支点时的荷载横向分布计算。 此时，主梁的支承刚度远大于主梁间横向联系
的刚度，荷载作用于某处时，基本上由相邻的两片 梁分担，并传递给支座，其受力特性与杠杆接近。 2、可用于双主梁桥(图5—44)，或横向联系很弱的 无中间横隔梁的桥梁。
为了求主梁所受的最大荷载，通常可利用反力 影响线来进行，在此情况下，它也就是计算荷载横
2、考虑主梁抗扭刚度的修正偏心压力法
1、根据平衡条件：
2、由材料力学知，简支梁考虑自由扭转时跨中截 面扭矩与扭角以及竖向力与挠度的关系为：
式中：J---- 为简支梁的跨度 ITj---- 梁的抗扭惯矩 G----- 材料的剪切模量
3、由几何关系[图5—49b)] 4、将式(5—43)代入， 5、则将上式代入与MTi的关系式，就得
由前述的偏心压力法知，荷载横向影响线坐标 的公式为：
上式中等号右边第一项是由中心荷载P＝1引起 的，此时各主梁只发生挠度而无转动，显然它与主 梁的抗扭无关。算式中没有计入主梁的抗扭作用。
等号右边第二项是由偏心力矩M＝1*e作用所引起， 此时由于截面的转动，各主梁不仅发生竖向挠度， 而且还必然同时引起扭转，但在计算式中没有计入 主梁的抗扭作用。因此，要计入主梁的抗扭影响， 只需对等式第二项给予修正。
第五节、荷载横向分布计算
ቤተ መጻሕፍቲ ባይዱ
(1)杠杆原理法，为把横向结构(桥面板和横隔粱)视 作在主梁上断开而简支在其上的简支梁。 (2)偏心压力法，为把横隔梁视作刚性极大的梁，当 计及主梁抗扭刚度影响时，此法又称为修正偏心压 力法。 (3)横向铰接板(梁)法，为把相邻板(梁)之间视作饺 接，只传递剪力。 (4)横向刚接梁法，为把相邻主梁之间视作刚性连 接，即传递剪力和弯短。 (5)比拟正交异性板法，为将主梁和横隔梁的刚度换 算成正交两个方向刚度不同的比拟弹性平板来求解。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章 荷载横向分布计算由于本桥各T 梁之间采用混凝与湿接缝刚性连接，故其荷载横向分布系数，在梁端可按“杠杆原理法”计算（m 0），在跨中按“修正刚性横梁法”计算(m c )。

（一）梁端的横向分布系数m 0根据桥规规定，在横向影响线确定荷载沿横向最不利的布置位置。

例如，对于汽车荷载，规定的汽车横向轮距为1.8m ，两列汽车车轮的横向最小间距为1.30m,车轮距离人行道缘石最少为0.50m 。

求出相应于荷载位置的影响线竖标值后，就可得到横向所有荷载分布给1号梁的最大荷载值为： 式子中：q P —汽车荷载轴重；q η—汽车车轮的影响线竖标。

由此可得：1号梁在汽车荷载作用下最不利荷载横向分布系数为654.001=m 同理有：904.002=m ；904.003=m ；904.004=m ；904.005=m ；654.006=m（二）跨中的横向分布系数m c 1.计算I 和I T求主梁截面中心位置a x (距梁顶)翼板的换算平均厚度 cm h 19224141=+=马蹄形下翼缘换算厚度 cm h 5.34228412=+=S ≈ (260-18)×19×19/2+245×18×245/2=583906cm 3 A ≈(260-18)×19+245×18=9008cm 2 重心距离 a x =S/A=583906/9008=64.82cm 主梁抗弯惯性矩：I ≈1/12×(260-18)×193+(260-18)×19×(64.82-19/2)2+1/12×18×2453 +18×245×(245/2-64.82)2=cm 4=0.5094m 4 翼板主梁抗扭惯性矩b 1/t 1=260/19=13.68＞10, 查表得c 1=0.33梁肋b 2=245-19=226cmb 2/t 2=226/18=12.6＞10, 查表得c 2=0.33 I T =∑c i b i t i 3=0.33×260×193+0.33×226×183=1023452cm 4=0.0102m 42.计算抗扭修正系数β本桥各主梁的横截面均相等，梁数n=6，梁间距为2.6m ，则 其中：E —混凝土弹性模量；G —混凝土剪切模量，E G 43.0=。

3.计算横向影响线竖标值对于1号边梁考虑抗扭修正厚的横向影响竖标值为：刚性横梁法的横向分布影响线为直线，设影响线零点离1号梁轴线的距离为x ，则：174.06.25508.0-⨯-=x x 解得：m x 68.9= 4.计算荷载横向分布系数1号边梁的横向影响和布载图如图所示。

5.同样地，按照上述步骤3.4可以算出其他梁的横向分布系数刚性横梁法的横向分布影响线为直线，设影响线零点离1号梁轴线的距离为x ，则：038.06.25371.0-⨯-=x x 解得：m x 12≈ 刚性横梁法的横向分布影响线为直线，设影响线零点离1号梁轴线的距离为x ，则：解得：m x 23≈根据对称性, 4、5、6号梁的横向分布系数：89.01=c m ；796.02=c m ；69.03=c m ； 89.06=c m ；796.05=c m ；69.04=c m第四章 主梁内力计算（一）.恒载集度 （1）跨内均布荷载主梁：[]m kN q /89.232618.045.213.026.028.026.01.08.016.082.11=⨯⨯+⨯+⨯+⨯+⨯=横隔板(预制部分)：[]mkN q /90.276.38/2662.013.01.04.0)6.018.06.2()16.028.045.2(22=⨯⨯⨯-⨯---⨯--=横隔板(现浇部分)：8 cm 厚W8级C50混凝土铺装层： 7cm 厚沥青混凝土铺装层： 防撞栏杆： （2）支座 主梁：横隔板(预制部分)：[]mkN q /26.276.38/2662.00475.019.0)6.06.06.2()16.028.045.2(2=⨯⨯⨯⨯---⨯--=横隔板(现浇部分）：8 cm 厚W8级C50混凝土铺装层： 7cm 厚沥青混凝土铺装层： 防撞栏杆：（二）1号T 梁内力计算和组合 1.支座截面内力计算： （1）一期恒载内力计算 支点处：0=x0=M ,（2）二期恒载内力计算 支点处：0=x0=M ,（3）活载由于本设计是按四车道来设计的，故查规范有：设计车道数为2时，00.1=ξ；设计车道数为3时，78.0=ξ；设计车道数为4时，67.0=ξ。

T 梁基频：ccm EI L f 212π=式中：L —主梁计算跨度，L=38.76m ； E c —混凝土弹性模量，E c =3.45×1010Pa ； I c —跨中截面的截面惯性矩，I c =0.597m 4； m c —跨中处的单位长度质量，m c =4083.59Ns 2/m 2。

查规范，可得冲击系数： 根据规范可知：公路I 级荷载中，m kN q k /5.10=，计算跨径m L 76.38=，kN P K 04.31576.385.10=⨯=，计算剪力效应时, K P 应乘以系数1.2。

计算活载内力时，要综合考虑车道折减系数，影响线，横向分布系数等因素。

对于边梁（1号梁）：00.1=ξ，654.00=m ，796.0=c m0m ax =M ，0=Q对应的有： 0=M采用三车道，则78.0=ξ，654.00=m ，89.0=c m0m ax =M ， 0=Q对应的有： 0=M可见，应该按照两车道布置，此时有： 支点处：0=x0m ax =M ,0=QkN Q 673.445max =，0m ax =M2.横截面变宽处 （1）一期恒载内力计算 变宽处：m x 5.3=（2）二期恒载内力计算 变宽处：m x 5.3= （3）活载计算活载内力时，要综合考虑车道折减系数，影响线，横向分布系数等因素。

对于边梁（1号梁）来说：（设计车道为1或4时候不满足要求） 采用两车道，则00.1=ξ，654.00=m ，796.0=c m 对应的有：采用三车道，则78.0=ξ，654.00=m ，89.0=c mmkN y P m M ii c ⋅=⨯⨯⨯+⨯⨯⨯⨯+=⋅⋅+=∑74.1300)1840.376.385.05.10184.304.315(89.078.0)1349.01()1(max ξμ 对应的有：可见，应该按照两车道布置，此时有： 变宽处：m x 5.3=m kN M ⋅=184.1377max ,kN Q 156.404= kN Q 479.405max =，m kN M ⋅=14393.1/4跨截面处（即第一片中横隔板处）： （1）一期恒载内力计算 1/4跨截面处：m x 69.9= （2）二期恒载内力计算 1/4跨截面处：m x 69.9= （3）活载计算活载内力时，要综合考虑车道折减系数，影响线，横向分布系数等因素。

对于边梁（1号梁）来说：（设计车道为1或4时候不满足要求） 采用两车道，则00.1=ξ，654.00=m ，735.0=c m 对应的有：采用三车道，则78.0=ξ，654.00=m ，89.0=c mmkN y P m M ii c ⋅=⨯⨯⨯+⨯⨯⨯⨯+=⋅⋅+=∑93.2968)2675.776.385.05.102675.704.315(89.078.0)1349.01()1(max ξμ对应的有：kNy m P Q ii i 516.306)07.296525.05.0(5.106525.004.3152.1[78.0)1349.01()1(max =⨯⨯⨯+⨯⨯⨯⨯+≈⋅⋅+=∑ξμ对应的有：mkN y P m M ii c ⋅=⨯⨯⨯+⨯⨯⨯⨯+=⋅⋅+=∑486.2617)2675.707.295.05.102675.704.315(89.078.0)1349.01()1(ξμ可见，应该按照两车道布置，此时有： 1/4跨截面处：m x 69.9=m kN M ⋅=43.3143max ,kN Q 41.321= kN Q 022.332max =，m kN M ⋅=89.28924.跨中截面：（1）一期恒载内力计算 跨中处：m x 38.19= （2）二期恒载内力计算 跨中处：m x 38.19=m kN M ⋅=-⨯⨯+++⨯=002.2492)38.1976.38(38.19)21.376.300.530.1(5.0kNQ 038.19)21.376.300.530.1(76.38)21.376.300.530.1(5.0=⨯+++-⨯+++⨯=（3）活载计算活载内力时，要综合考虑车道折减系数，影响线，横向分布系数等因素 对于边梁（1号梁）来说：（设计车道为1或4时候不满足要求） 采用两车道，则00.1=ξ，654.00=m ，796.0=c m 对应的有： 对应的有：采用三车道，则78.0=ξ，654.00=m ，89.0=c m对应的有： 对应的有：mkN y P m M ii c ⋅=⨯⨯⨯+⨯⨯⨯⨯+=⋅⋅+=∑494.33871)69.938.195.05.1069.904.315(89.078.0)1349.01()1(ξμ可见，应该按照两车道布置，此时有： 跨中处：m x 38.19=m kN M ⋅=08.4539max ,kN Q 675.157=kN Q 11.200max =，m kN M ⋅=43.3648表1 一期恒载作用下边梁（1号梁）的计算结果截面位置 弯矩—M （kN·m ） 剪力—Q （kN ） 支座截面处 0 553.753 横截面变宽度处 1653.077 425.425 1/4跨截面处 3773.215 259.595 跨中截面处5030.953表2 二期恒载作用下边梁（1号梁）的计算结果截面位置 弯矩—M （kN·m ） 剪力—Q （kN ） 支座截面处 0 257.173 横截面变宽度处 818.825 210.728 1/4跨截面处 1869.002 128.586 跨中截面处2492.002表3 活载（公路—I 级）作用下边梁（1号梁）的计算结果截面位置 M max （kN ·m ） 相应Q （kN ） Q max （kN ） 相应M （kN ·m ）支座截面处 0 0 445.673 0 横截面变宽度处 1481.48 404.156 405.479 1439 1/4跨截面处 4539.08 321.41 332.022 3648.43 跨中截面处4191.241157.675200.113648.435.承载能力极限状态下效应组合（对边梁而言）荷载基本组合设计值表达式为：上式中，由于本设计的设计安全等级为二级，故有0.10=γ，分项系数2.1=G γ，4.1=Q γGik S 见表1和表2，k Q S 1见表3，Qjk S 没有值。