横向分布系数计算(多种方法计算)

横向分布系数荷载横向分布系数：表示某根主梁所承担的最大荷载占各个轴重的倍数。

为使荷载横向分布的计算能更好地适应各种类型的结构特性，就需要按不同的横向结构简化计算模型拟定出相应的计算方法。

目前最常用的几种方法：杠杆原理法：把横向结构（桥面板和横隔梁）视作在主梁上断开而简支在其上的简支梁。

适用于双主梁桥、荷载位于靠近主梁支点处。

偏心压力法：把横隔梁视作刚性极大的梁，故又称刚性横梁法。

当计及主梁抗扭刚度影响时此法又称为修正偏心压力法（修正刚性横梁法）。

适用于窄桥（宽跨比B /l 小于或接近0.5的情况）。

G-M 法：由比拟正交异性板法发展而来，能利用计算机工具或编就的计算图表得出相对来说比较精确的结果。

此法概念明确，计算简捷，对于各种桥面净空宽度和多种荷载组合的情况，可以很快的求出各片主梁的相应内力值。

例：如图所示桥梁横断面，在公路-Ⅰ级荷载作用下，分别用杠杆原理法和偏心压力法求①和②号梁的荷载横向分布系数。

杠杆原理法：首先在①号梁和②号梁横向影响线上，按最不利方式布载，如图所示：①号梁：11900180011219002m −=×+× 11110.0530.521922=×+≈×+ 0.5265= ②号梁：1190018001119001300121900221900m −−=×+×+× 1111611 10.0530.50.316219221922=×+×+×≈×++× 0.6845=偏心压力法：首先画①号梁和②号梁横向影响线，那就要先找到其影响线的两个控制竖标值，由于各主梁的截面均相同，故可按下式计算：()()()()()()422222212341122222221112122114212121 1.5 1.90.5 1.90.5 1.9 1.5 1.918.05m 1.5 1.911=0.250.450.7418.051.5 1.911=0.250.450.2418.051=n ii i i n ii n i i i a a a a a a a n a a n a a a n a ηηη=====+++=×+×+−×+−×=×+=+=+=×−=−=−=−×+∑∑∑∑()()()()212424210.5 1.9 1.5 1.910.250.150.4418.050.5 1.9 1.5 1.911=0.250.150.1418.05n i ni i a a n aη==×××=+=+=××××−=−=−=∑∑然后在①号梁和②号梁横向影响线上，按最不利方式布载，如图所示：①号梁：()10.7160.4320.2260.508=0.6582m =×++− ②号梁：()10.4050.3110.2420.147=0.55252m =×+++ 荷载横向分布系数延桥垮的变化：通常用“杠杆原理法”来计算荷载位于支点处的横向分布系数m 0，其他方法均适用于计算荷载位于跨中的横向分布系数m c 。

空心板横向分布系数
空心板的横向分布系数（also known as the flexural distribution factor or shear distribution factor）是指在横向荷载作用下，板
的弯矩或剪力在截面内的分布情况。

横向分布系数是根据板的几何形状和材料特性来计算的。

对于矩形横断面的空心板，横向分布系数可以通过以下公式计算：
α = 1 - 0.4 × (h/d)
其中，α为横向分布系数，h为板的高度，d为内缘边距离。

横向分布系数的值范围从0到1，其中1表示均匀分布，0表
示完全集中在板的内侧边缘。

横向分布系数的值对于确定板的设计弯矩或剪力分配至关重要。

较高的横向分布系数表示板对荷载的弯矩或剪力在截面内更均匀地分布，从而减小了构件的局部破坏风险。

需要注意的是，横向分布系数仅适用于符合一定几何条件的空心板，并且基于假设材料的弹性行为。

在实际设计中，仍需根据具体情况和施工要求进行结构分析和验证。

桥梁荷载横向分布系数的各种计算方法综述姓名：XXX学号：50XXXXXXX3摘要：公路桥梁荷载横向分布有多种计算模型，其中比较实用的有：1）杠杆原理法；2）偏心压力法、修正偏心压力法；3）铰接板（梁）法；4）刚接板（梁）法等。

这些理论方法有各自的适用范围，应按具体情况选用适当的方法来运用。

关键词：混凝土简支梁桥；荷载横向分布系数；影响线；影响因素1引言随着国民经济的发展，对交通的需求日益提高，众多的高速公路及城市快速干道相继修建。

公路桥梁上行驶车辆的轴重加重、速度提高，车流密度也相应提高。

使之在设计过程中如何确保桥梁结构在使用寿命期限内的安全性，准确计算各片梁所需承担的最大活载弯矩就显得尤为重要。

特别是对于中小跨多片梁型的桥梁，当跨数较多时，用测试横向分布状态的方法对桥梁运营状态进行评价，具有简洁、实用、可靠等优点，具有较高的推广价值。

所谓荷载横向分布系数（Lateral Distribution Factor of Live Load）是指公路车辆荷载在桥梁横向各主梁间分配的百分数。

普通简支桥梁中它和各主梁间的联结方式（铰接或刚接），有无内横梁及其数目，断面的抗弯刚度和抗扭刚度，以及车辆荷载在桥上的位置等有关。

它是一个复杂的空间结构问题，在桥梁设计中常简化为平面问题而引用荷载横向分布系数。

[1]目前广泛采用的是利用主梁的纵向影响线和它的荷载横向分布影响线相结合的方法，荷载横向分布系数是在荷载横向分布影响线的基础上按荷载的最不利位置布载，并将荷载位置相应的影响线竖标值求和得到的最后数值结果。

对于混凝土简支梁桥，荷载横向分布系数的影响因素主要有桥粱跨度(Z)、主梁间距(S)、桥面板的厚度(t0)、主梁刚度(K0)、横隔梁(板)的数量及位置、车载类型及布栽位置、车辆间距、栏杆及横跨比等。

[2][3][4][9]2计算方法及其适用范围荷载横向分布理论在桥梁设计中占有重要地位。

目前桥梁荷载横向分布系数常用的计算方法主要有杠杆原理法、偏心压力法（修正偏心压力法）、铰接板（梁）法、刚接梁法和比拟正交异性板法（G-M法）等。

桥梁荷载横向分布系数计算方法桥梁是交通系统中重要的基础设施，承载着大量的车辆和行人荷载。

桥梁荷载横向分布系数的计算对于桥梁设计和施工具有重要意义。

本文将详细介绍桥梁荷载横向分布系数的计算方法，包括计算原理、步骤和注意事项，并通过具体算例进行分析和说明。

桥梁荷载是指作用在桥梁上的各种力量，包括车辆荷载、人群荷载、风荷载等。

横向分布系数是用来描述桥梁荷载在桥面横向分布的系数，其大小与桥梁的形状、结构形式等因素有关。

桥梁荷载横向分布系数的计算是桥梁设计的重要环节，也是施工过程中的关键步骤。

计算桥梁荷载横向分布系数的方法可以分为理论计算和数值模拟两种。

理论计算方法包括集中力作用下的横向分布系数计算和均布力作用下的横向分布系数计算。

数值模拟方法则是利用计算机进行模拟分析，得到更精确的横向分布系数。

根据集中荷载作用下的弯矩和剪力，计算横向分布系数。

根据车道均布荷载的弯矩和剪力，计算横向分布系数。

数值模拟方法可以利用有限元软件进行模拟分析，得到更精确的横向分布系数。

具体步骤如下：通过对模型的应力、应变等进行分析，得出横向分布系数。

下面通过一个简单的算例来说明桥梁荷载横向分布系数的计算方法。

该桥梁为简支梁结构，跨度为20米，桥面宽度为10米。

车辆荷载为50吨的重车，速度为20公里/小时，作用在桥上长度为10米。

通过集中力作用下的横向分布系数计算方法，来计算该桥梁的横向分布系数。

计算桥梁单位长度的自重为5吨/米。

然后，确定车辆荷载的大小为50吨，位置为桥面中心线偏左1米处。

根据车辆荷载作用下的弯矩和剪力，可以得出横向分布系数为67。

根据横向分布系数的定义可知，该桥梁在车辆荷载作用下的横向分布系数为67。

桥梁荷载横向分布系数的计算是桥梁设计和施工中的重要环节，对于保证桥梁的安全性和正常使用具有重要意义。

本文详细介绍了桥梁荷载横向分布系数的计算方法，包括计算原理、步骤和注意事项，并通过具体算例进行了分析和说明。

随着计算机技术和数值模拟方法的发展，未来的研究方向将更加倾向于开发更加精确、便捷的计算方法和模型，以便更好地应用于实际工程中。

一、 横向分布如图3—2—1a所示，梁桥的上部结构由承重结构（①~④号主梁）及传力结构（横隔梁、行车道板）两大部分组成，各片主梁靠横隔梁和行车道板连成空间整体结构，当桥上作用荷载（桥面板上作用2个车轴，前轴轴重为P1，后轴轴重为P2）时，各片主梁共同参与工作，形成了各片主梁之间的内力分布。

在计算恒载时，除主梁的自重外，一般将桥面铺装、人行道、栏杆等的重量近似平均分配给各片主梁，即计算出桥面铺装、人行道、栏杆等的总重量除以梁的片数（本例4片梁），得到每片主梁承担的桥面铺装、人行道、栏杆的重量。

由于人行道、栏杆等构件一般位于边梁上（①、④号主梁），精确计算时，也可考虑它们的重量在各梁间的分布，即中梁（②、③号主梁）也分担一部分人行道、栏杆的重量。

在计算活载时，需要考虑活载在各片主梁间的分布。

《标准》规定，车道荷载的横向分布系数应按设计车道数布置车辆荷载进行计算。

车辆荷载的横向布置如图3—2—1c所示。

对于车道荷载，最外车轮距人行道缘石之距不得小于0.5m，车道荷载的横向轮距为1.8m，两列车道荷载车轮的横向间距不得小于1.3m。

如图3—2—1b所示，在车道荷载的作用下，①号边梁所分担的荷载，也就是说，①号边梁所分担的荷载R1为轴重P1的。

若将第i号梁所承担的力R i表示为系数m i与轴重P的乘积（R i=m i×P），则m i称为第i号梁的荷载横向分布系数。

由此，1号梁的横向分布系数。

荷载所引起的各片主梁的内力大小（横向分布）与桥梁的构造特点、荷载的作用位置有关，因此求解荷载作用下各主梁的内力是一个空间问题，目前广泛采用的方法是将复杂的空间问题转化为平面问题。

本节将着重介绍几种横向分布系数的计算方法。

二、杠杆法基本原理：杠杆法忽略了主梁之间横向结构的联系作用，即假设桥面板在主梁上断开，把桥面板看作沿横向支承在主梁上的简支梁或悬臂梁。

如图3—2—1b所示，由于杠杆法忽略了主梁之间横向结构的联系作用，当桥上作用车道荷载时，左边的轮重P1/2仅传递给1号和2号梁，右边的轮重P1/2传递给2号梁和3号梁。

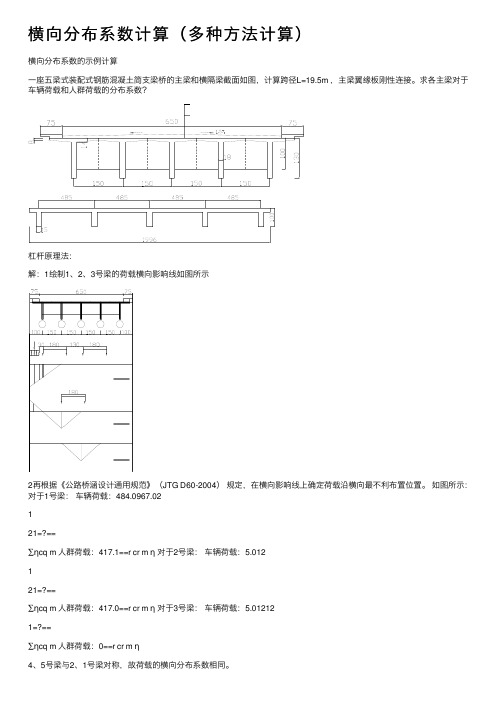
横向分布系数计算（多种⽅法计算）横向分布系数的⽰例计算⼀座五梁式装配式钢筋混凝⼟简⽀梁桥的主梁和横隔梁截⾯如图，计算跨径L=19.5m ，主梁翼缘板刚性连接。

求各主梁对于车辆荷载和⼈群荷载的分布系数？杠杆原理法：解：1绘制1、2、3号梁的荷载横向影响线如图所⽰2再根据《公路桥涵设计通⽤规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。

如图所⽰：对于1号梁：车辆荷载：484.0967.02121=?==∑ηcq m ⼈群荷载：417.1==r cr m η对于2号梁：车辆荷载：5.012121=?==∑ηcq m ⼈群荷载：417.0==r cr m η对于3号梁：车辆荷载：5.012121=?==∑ηcq m ⼈群荷载：0==r cr m η4、5号梁与2、1号梁对称，故荷载的横向分布系数相同。

偏⼼压⼒法（⼀）假设：荷载位于1号梁 1长宽⽐为26.25.155.19>=?=b l ，故可按偏⼼压⼒法来绘制横向影响线并计算横向分布系数c m 。

本桥的各根主梁的横截⾯积均相等，梁数为5，梁的间距为1.5m ，则：5.220)5.11(2)5.12(2222524232221512=+?+?=++++=∑=a a a a a ai i2所以1号5号梁的影响线竖标值为：6.0122111=+=∑i a a n η 2.0122115-=-=∑i a a n η由11η和15η绘制荷载作⽤在1号梁上的影响线如上图所⽰，图中根据《公路桥涵设计通⽤规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。

进⽽由11η和15η绘制的影响线计算0点得位置，设0点距离1号梁的距离为x ，则：4502.015046.0=?-?=x xx 0点已知，可求各类荷载相应于各个荷载位置的横向影响线竖标值3计算荷载的横向分布系数车辆荷载：()533.0060.0180.0353.0593.02121=-++?==∑ηcq m ⼈群荷载：683.0==r cr m η（⼆）当荷载位于2号梁时与荷载作⽤在1号梁的区别以下：4.0122112=+=∑i a a a n η0122552=-=∑ia a a n η其他步骤同荷载作⽤在1号梁时的计算修正偏⼼压⼒法（⼀）假设：荷载位于1号梁 1计算I 和T I ：2.3813018)2814(150)18150()2814(1301821)(2122221=?++?-+++??=+-++?=ch bd c b d ch y8.912.3813012=-=-=y y y[][]43333313132106543)112.38)(18150(2.381508.911831))((31cm d y c b by cy I ?=---?+??=---+?=对于翼板1.0073.01501111<==b t ，对于梁肋151.0119 1822==b t 查下表得所以：311=c ，301.02=c 433331027518119301.01115031cm t b c I i i i T ?=??+??==∑2计算抗扭修正系数β与主梁根数有关的系数ε则n=5，ε=1.042 G=0.425E875.055.15.1910654310275425.0042.111)(112332=??+=+=E E B l EI GI T εβ 3计算荷载横向影响线竖标值11η和15η55.0122111=+=∑i a a n βη 15.0122115-=-=∑ia a n βη由11η和15η绘制荷载作⽤在1号梁上的影响线如上图所⽰，图中根据《公路桥涵设计通⽤规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。

桥梁荷载横向分布系数的各种计算方法综述姓名：XXX 学号：50XXXXXXX3摘要：公路桥梁荷载横向分布有多种计算模型，其中比较实用的有：1）杠杆原理法；2）偏心压力法、修正偏心压力法；3）铰接板（梁）法；4）刚接板（梁）法等。

这些理论方法有各自的适用范围，应按具体情况选用适当的方法来运用。

关键词：混凝土简支梁桥；荷载横向分布系数；影响线；影响因素1 引言随着国民经济的发展，对交通的需求日益提高，众多的高速公路及城市快速干道相继修建。

公路桥梁上行驶车辆的轴重加重、速度提高，车流密度也相应提高。

使之在设计过程中如何确保桥梁结构在使用寿命期限内的安全性，准确计算各片梁所需承担的最大活载弯矩就显得尤为重要。

特别是对于中小跨多片梁型的桥梁，当跨数较多时，用测试横向分布状态的方法对桥梁运营状态进行评价，具有简洁、实用、可靠等优点，具有较高的推广价值。

所谓荷载横向分布系数（Lateral Distribution Factor of Live Load）是指公路车辆荷载在桥梁横向各主梁间分配的百分数。

普通简支桥梁中它和各主梁间的联结方式（铰接或刚接），有无内横梁及其数目，断面的抗弯刚度和抗扭刚度，以及车辆荷载在桥上的位置等有关。

它是一个复杂的空间结构问题，在桥梁设计中常简化为平面问题而引用荷载横向分布系数。

[1]目前广泛采用的是利用主梁的纵向影响线和它的荷载横向分布影响线相结合的方法，荷载横向分布系数是在荷载横向分布影响线的基础上按荷载的最不利位置布载，并将荷载位置相应的影响线竖标值求和得到的最后数值结果。

对于混凝土简支梁桥，荷载横向分布系数的影响因素主要有桥粱跨度(Z)、主梁间距(S)、桥面板的厚度(t0)、主梁刚度(K0)、横隔梁(板)的数量及位置、车载类型及布栽位置、车辆间距、栏杆及横跨比等。

[2][3][4][9]2 计算方法及其适用范围荷载横向分布理论在桥梁设计中占有重要地位。

目前桥梁荷载横向分布系数常用的计算方法主要有杠杆原理法、偏心压力法（修正偏心压力法）、铰接板（梁）法、刚接梁法和比拟正交异性板法（G-M法）等。

1、偏载时支点(杠杆法)过渡到跨中(偏压法)，对称布载时采用杠杆法偏心布载时横向分配系数Mc计算图示对称布载时横向分配系数Mc计算图示->|<-支点过渡跨中比值=0.25指分界点在1/4计算跨径处插值计算偏压法横分系数插值计算|<----->|<-------------------->|<----->|Mc(杠杆法) Mc(杠杆法) Mc(杠杆法)+ + +--------------------------------------+| \ Mc(偏心受压法) / | | || +----------------------+ | | || | | |+--------------------------------------++--------------------------------------+左支点梁板跨中右支点2、左右偏载均采用偏心受压法，对称布载采用杠杆法偏心布载时横向分配系数Mc计算图示对称布载时横向分配系数Mc计算图示Mc(偏心受压法) Mc(杠杆法)+--------------------------------------++--------------------------------------+| | | || | | || | | |+--------------------------------------++--------------------------------------+左支点梁板跨中右支点3、完全杠杆法，即左右偏载或对称布载均采用杠杆法计算图示略。

当2柱时可采用“左右偏载均采用偏心受压法，对称布载采用杠杆法”当3柱及以上时可采用“偏载时支点(杠杆法)过渡到跨中(偏压法)，对称时杠杆法”，即纵向轮轴位于支点与1/4计算跨径(假设偏载支点过渡跨中比值0.25)之间按“杠杆法”与“偏心受压法”插值计算，1/4计算跨径之间按“偏心受压法”计算。

看大家对横向力分布系数计算疑惑颇多，特在这里做一期横向力分布系数计算教程（本教程讲的比较粗浅，适用于新手）。

总的来说，横向力分布系数计算归结为两大类（对于新手能够遇到的）：1、预制梁（板梁、T梁、箱梁）这一类也可分为简支梁和简支转连续2、现浇梁（主要是箱梁）首先我们来讲一下现浇箱梁（上次lee_2007兄弟问了，所以先讲这个吧）在计算之前，请大家先看一下截面这是一个单箱三室跨径27+34+27米的连续梁，梁高1.55米，桥宽12.95米！！支点采用计算方法为为偏压法（刚性横梁法）mi=P/n±P×e×ai/(∑ai x ai)跨中采用计算方法为修正偏压法（大家注意两者的公式，只不过多了一个β）mi=P/n±P×e×ai×β/(∑ai x ai)β---抗扭修正系数β=1/(1+L^2×G×∑It/(12×E×∑ai^2 Ii)其中：∑It---全截面抗扭惯距Ii ---主梁抗弯惯距Ii=K Ii` K 为抗弯刚度修正系数，见后L---计算跨径G---剪切模量G=0.4E 旧规范为0.43EP---外荷载之合力e---P对桥轴线的偏心距ai--主梁I至桥轴线的距离在计算β值的时候，用到了上次课程/thread-54712-1-1.html我们讲到的计算截面几何性质中的抗弯惯矩和抗扭惯矩，可以采用midas计算抗弯和抗扭，也可以采用桥博计算抗弯，或者采用简化截面计算界面的抗扭，下面就介绍一下这种大箱梁是如何简化截面的：简化后箱梁高度按边肋中线处截面高度(1.55m)计算，悬臂比拟为等厚度板。

①矩形部分(不计中肋):计算公式:It1=4×b^2×h1^2/(2×h/t+b/t1+b/t2)其中：t,t1,t2为各板厚度h,b为板沿中心线长度h为上下板中心线距离It1=4×((8.096+7.281)/2)^2×1.34^2/(2×1.401/0.603+8.097/0.22+7.281/0.2)=5.454 m4②悬臂部分计算公式: It2=∑Cibiti3其中：ti,bi为单个矩形截面宽度、厚度Ci为矩形截面抗扭刚度系数,按下式计算:Ci=1/3×(1-0.63×ti/bi + 0.052×(ti/bi)^5)=1/3×(1-0.63×0.26/2.2+0.052×(0.26/2.2)^5)=0.309It2=2×0.309×2.2×0.26^3=0.0239 m4③截面总的抗扭惯距It= It1+ It2=5.454+0.0239=5.4779 m4大家可以用midas计算对比一下看看简化计算和实际能差多少？？先计算一下全截面的抗弯和中性轴，下面拆分主梁需要用的到采用<<桥梁博士>>V2.9版中的截面设计模块计算全截面抗弯惯距，输出结果如下：<<桥梁博士>>---截面设计系统输出文档文件: D: \27+34+27.sds文档描述: 桥梁博士截面设计调试任务标识: 组合截面几何特征任务类型: 截面几何特征计算------------------------------------------------------------截面高度: 1.55 m------------------------------------------------------------计算结果:基准材料: JTJ023-85: 50号混凝土基准弹性模量: 3.5e+04 MPa换算面积: 7.37 m2换算惯矩: 2.24 m4中性轴高度: 0.913 m沿截面高度方向5 点换算静矩(自上而下):主截面:点号: 高度(m): 静矩(m××3):1 1.55 0.02 1.16 1.773 0.775 1.834 0.388 1.585 0.0 0.0------------------------------------------------------------计算成功完成结果：I全= 2.24 m4 中性轴高度H=0.913m下面来讲一下主梁拆分的原则：将截面划分为τ梁和I梁,保持将两截面中性轴与全截面中性轴位置一致。