材料力学5-弯曲强度

第 五 章 弯 曲 应 力一、是非判断题1、设某段梁承受正弯矩的作用，则靠近顶面和靠近底面的纵向纤维分别是伸长的和缩短的。

（ × ）2、中性轴是梁的横截面与中性层的交线。

梁发生平面弯曲时，其横截面绕中性轴旋转。

（ √ ）3、 在非均质材料的等截面梁中，最大正应力maxσ不一定出现在maxM的截面上。

（ × ）4、等截面梁产生纯弯曲时，变形前后横截面保持为平面，且其形状、大小均保持不变。

（ √ ）5、梁产生纯弯曲时，过梁内任一点的任一截面上的剪应力都等于零。

（ × ）6、控制梁弯曲强度的主要因素是最大弯矩值。

（ × ）7、横力弯曲时，横截面上的最大切应力不一定发生在截面的中性轴上。

（ √ ）@二、填空题1、应用公式zMy I 时，必须满足的两个条件是 满足平面假设 和 线弹性 。

2、跨度较短的工字形截面梁，在横力弯曲条件下，危险点可能发生在 翼缘外边缘 、 翼缘腹板交接处 和 腹板中心 处。

3、 如图所示的矩形截面悬臂梁，其高为h 、宽为b 、长为l ，则在其中性层的水平剪力=S FbhF23 。

4、梁的三种截面形状和尺寸如图所示，则其抗弯截面系数分别为226161bH BH -、xH Bh BH 66132- 和 Hbh BH 66132- 。

三、选择题1、如图所示，铸铁梁有A ，B ，C 和D 四种截面形状可以供选取，根据正应力强度，采用（ C ）图的截面形状较合理。

2、 如图所示的两铸铁梁，材料相同，承受相同的载荷F。

则当F 增大时，破坏的情况是 （ C ）。

A 同时破坏 ；B （a ）梁先坏 ；C （b ）梁先坏3、为了提高混凝土梁的抗拉强度，可在梁中配置钢筋。

若矩形截面梁的弯矩图如图所示，则梁内钢筋（图中虚线所示）配置最合理的是（D ）ABCDHABC D?四、计算题&1、长为l 的矩形截面梁，在自由端作用一集中力F ，已知m h 18.0=，m b 12.0=，m y 06.0=，m a 2=，kN F 1=，求C 截面上K 点的正应力。

弯曲强度与弯曲模量的关系1.引言1.1 概述概述弯曲强度和弯曲模量都是材料力学性能的重要指标，它们描述了材料在受到外部力作用时的抵抗变形和破坏能力。

弯曲强度是指材料在弯曲加载下抵抗破坏的能力，通常用抗弯强度来表示；而弯曲模量则描述了材料在受到外力作用时的抵抗变形能力，它代表了材料的刚性程度。

在工程实践中，了解材料的弯曲强度和弯曲模量对于正确选择材料并进行结构设计具有重要意义。

通过研究材料的弯曲强度和弯曲模量之间的关系，可以了解材料的力学性能和耐久性，并为工程实践中的材料选择、力学设计以及预测材料的破坏行为提供参考依据。

本文将首先对弯曲强度和弯曲模量进行定义和测量方法的介绍，包括常见的试验方法和计算公式。

接着，将分析弯曲强度和弯曲模量之间的关系，探讨两者之间的影响因素和相互作用机制。

最后，将讨论弯曲强度和弯曲模量在实际应用中的意义，并讨论影响其数值的因素，以及如何通过工程手段来调控和优化这些性能。

通过深入研究弯曲强度和弯曲模量之间的关系，有助于我们更好地理解材料的力学性能和行为，为工程实践提供科学依据，并推动材料科学和工程领域的发展和进步。

最后，本文将总结研究结果，提出一些对未来研究的展望。

文章结构部分的内容应该包括对整篇文章的结构和各个章节内容的简要描述。

下面是对文章结构部分的一种可能描述：1.2 文章结构本文主要探讨弯曲强度与弯曲模量之间的关系，并分析在实际应用中的意义和影响因素。

文章按照以下章节组织：2.1 弯曲强度的定义和测量方法这一章节首先介绍了弯曲强度的定义，即在外力作用下材料能够承受的最大弯曲应力。

接着详细探讨了测量弯曲强度的方法，包括三点弯曲试验和四点弯曲试验等。

2.2 弯曲模量的定义和测量方法在本章节中，我们首先给出了弯曲模量的定义，即在弯曲过程中材料对应力的抵抗能力。

然后，我们将深入讨论测量弯曲模量的方法，如静态三点弯曲试验和动态振动试验等。

3. 结论在本章节中，我们将对弯曲强度与弯曲模量的关系进行分析和总结。

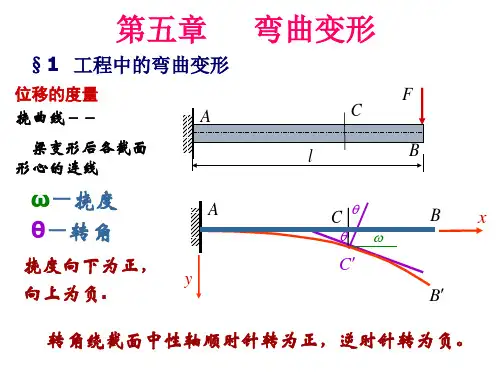
第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁，火车的轮轴，楼房的横梁，阳台的挑梁等。

二、弯曲的概念：受力特点——作用于杆件上的外力都垂直于杆的轴线。

变形特点——杆轴线由直线变为一条平面的曲线。

三、梁的概念：主要产生弯曲变形的杆。

四、平面弯曲的概念：受力特点——作用于杆件上的外力都垂直于杆的轴线，且都在梁的纵向对称平面内（通过或平行形心主轴且过弯曲中心）。

变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。

五、弯曲的分类：1、按杆的形状分——直杆的弯曲；曲杆的弯曲。

2、按杆的长短分——细长杆的弯曲；短粗杆的弯曲。

3、按杆的横截面有无对称轴分——有对称轴的弯曲；无对称轴的弯曲。

4、按杆的变形分——平面弯曲；斜弯曲；弹性弯曲；塑性弯曲。

5、按杆的横截面上的应力分——纯弯曲；横力弯曲。

六、梁、荷载及支座的简化（一）、简化的原则：便于计算，且符合实际要求。

（二）、梁的简化：以梁的轴线代替梁本身。

（三）、荷载的简化：1、集中力——荷载作用的范围与整个杆的长度相比非常小时。

2、分布力——荷载作用的范围与整个杆的长度相比不很小时。

3、集中力偶（分布力偶）——作用于杆的纵向对称面内的力偶。

（四）、支座的简化：1、固定端——有三个约束反力。

2、固定铰支座——有二个约束反力。

3、可动铰支座——有一个约束反力。

（五）、梁的三种基本形式：1、悬臂梁：2、简支梁：3、外伸梁：（L 称为梁的跨长） （六）、静定梁与超静定梁静定梁：由静力学方程可求出支反力，如上述三种基本形式的静定梁。

超静定梁：由静力学方程不可求出支反力或不能求出全部支反力。

§5—2 弯曲内力与内力图一、内力的确定（截面法）：[举例]已知：如图，F ，a ，l 。

求：距A 端x 处截面上内力。

解：①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力：剪力和弯矩1. 弯矩：M ；构件受弯时，横截面上存在垂直于截面的内力偶矩。

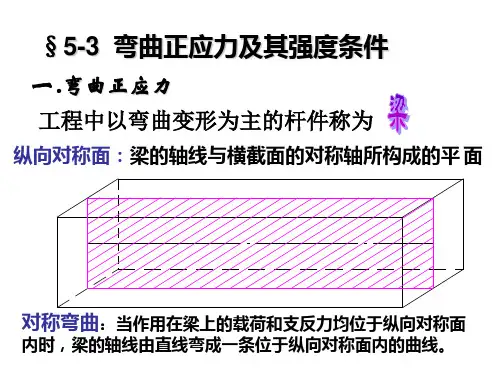
弯曲强度单位材料力学弯曲强度（抗弯强度）是指材料抵抗弯曲不断裂的能力，主要用于考察陶瓷等脆性材料的强度。

一般采用三点抗弯测试或四点测试方法评测。

其中四点测试要两个加载力，比较复杂；三点测试常用。

其值与承受的额定压力成正比。

又称挠曲强度或抗弯强度，在试件的两支点之间施加载荷，至试件破坏时的单位面积载荷值。

1.抗弯强度-特点机械性能：当材料受外力时表现出来的各种力学性能。

2.应力：当材料受外力时材料内部对外力的反应。

应力的大小用下述公式表示：应力（δ）＝作用（F）/材料单位面积（A），单位为Pa。

3.应变：当材料受外力作用时引起的形变。

应变的大小用下述公式表示：应变（ε）＝变化长度（△L）/初始长度（L）。

4.拉应力或张应力：材料受到拉伸时的内部应力。

5.压应力或压缩应力：材料受到压缩时的内部应力。

6.剪应力：材料受到切错作用力时，相互平行的部分发生滑动时的内部应力。

但当某一段材料或修复体受力时，往往是三种应力形式同时存在。

例如：咀嚼压力作用于固定桥时，桥体倪面受到的力为压应力，桥体的龈底则为拉应力，基牙修复体与桥体连接处为剪应力。

7.抗拉强度或抗张强度。

8.压缩强度或抗压强度：在试件上施加压缩载荷，至试件破坏时的单位面积载荷值。

9.弯曲强度：又称挠曲强度或抗弯强度，在试件的两支点之间施加载荷，至试件破坏时的单位面积载荷值。

10.硬度：材料抵抗其它硬物压入引起凹陷变形的能力。

常用的硬度单位有布氏硬度（HB或BHN），维氏硬度（Hv或VHN），洛氏硬度（HRA、HRC或RHN）奴氏硬度（HK或KHN）。

材料的表面硬度是其强度、比例极限、韧性、延展性及抗磨损、抗切割能力等多种性质综合作用的结果。

材料力学弯曲强度（抗弯强度）试验机，PY-H609弯曲挺度测定仪，深圳市普云电子有限公司11.冲击强度）：材料在冲击力作用下折断所需的能量。

12.延性和展性：延性是材料在拉力作用下不折断而经受恒久变形的能力。

展性是材料在压力作用不折断而经受恒久变形的能力。

石材弯曲强度计算公式石材弯曲强度是指石材在受到外力作用时，能够抵抗弯曲变形或破坏的能力。

弯曲强度是评估石材弯曲抗力的重要指标，对于石材的工程应用非常重要。

下面是一些相关参考内容及计算公式。

1. 石材的物理力学性质石材的物理力学性质包括密度、抗压强度、抗拉强度等。

在弯曲强度计算中尤为重要的是抗压强度和抗拉强度。

抗压强度是指石材能够抵抗垂直于其表面的压力的能力，抗拉强度是指石材能够抵抗垂直于其表面的拉力的能力。

常用符号表示为：抗压强度：f_c抗拉强度：f_t2. 单纯弯曲破坏假设在弯曲强度的计算中，常采用单纯弯曲破坏假设，即假设在弯曲中仅发生抗拉和抗压两种破坏。

这是一个简化的假设，可以用来计算石材的最小弯曲强度。

3. 弯曲破坏时的应力分布在弯曲过程中,石材受到的弯曲应力的最大值发生在材料的外纤维处。

根据力学原理，最大应力的计算公式为：σ_max = (M * y) / I其中，σ_max 为最大应力，M 为弯矩，y 为截面离中性轴的距离， I 为抵抗截面变形的截面惯性矩。

4. 弯曲应力与弯曲强度的关系弯曲应力与弯曲强度之间的关系可以用弯曲强度公式来表示。

根据材料力学原理，弯曲强度计算公式为：f_b = (M * y) / (b * d^2)其中，f_b 为弯曲强度，M 为弯矩，y 为截面离中性轴的距离，b 为截面的宽度， d 为截面的高度。

5. 弯曲强度的影响因素石材的弯曲强度受多种因素影响，包括石材的物理力学性质、构件几何形状、荷载作用形式等。

在计算弯曲强度时，需要综合考虑这些因素。

6. 相关标准和规范各个国家和地区都有相应的石材测试标准和规范，用于评估石材的性能和强度。

例如，中国国家标准《天然建筑石材裂纹弯曲强度测定方法》(GB/T 19698-2006)提供了相关测试方法和计算公式。

综上所述，石材弯曲强度的计算公式涵盖了材料的物理力学性质、弯曲破坏假设、应力分布、力学原理等多个方面。

在实际工程应用中，根据具体情况选择合适的公式和测试标准非常重要，以保证石材的安全、可靠性能。

材料弯曲强度材料的弯曲强度是指材料在受到外力作用下，抵抗弯曲变形和破坏的能力。

它是材料力学性能中的重要指标之一，对于工程材料的选择和设计具有重要意义。

在实际工程中，我们常常需要对材料的弯曲强度进行测试和分析，以确保材料的可靠性和安全性。

材料的弯曲强度受多种因素影响，其中包括材料的组织结构、化学成分、加工工艺等。

在进行弯曲强度测试时，我们需要考虑这些因素，并采取相应的措施进行测试和分析。

首先，我们需要选择合适的测试方法和设备。

常用的测试方法包括三点弯曲测试和四点弯曲测试。

在进行测试时，我们需要根据具体情况选择合适的测试方法，并确保测试设备的精度和稳定性。

其次，我们需要准备好测试样品。

测试样品的准备需要严格按照标准规范进行，包括样品的尺寸、形状、表面处理等。

在样品准备过程中，我们需要注意避免引入人为因素，以确保测试结果的准确性和可靠性。

测试过程中，我们需要严格控制测试条件，包括加载速度、加载方式、环境温湿度等。

在测试过程中，我们需要实时监测样品的变形和破坏情况，并记录测试数据。

在测试结束后，我们需要对测试数据进行分析和处理，得出样品的弯曲强度指标。

最后，我们需要根据测试结果进行评估和应用。

根据样品的弯曲强度指标，我们可以对材料的选择和设计进行指导，以确保工程的可靠性和安全性。

总之，材料的弯曲强度是材料力学性能中的重要指标，对于工程材料的选择和设计具有重要意义。

在进行弯曲强度测试时，我们需要选择合适的测试方法和设备，准备好测试样品，严格控制测试条件，对测试结果进行分析和评估。

只有这样，我们才能得出准确可靠的测试结果，并为工程设计和实践提供有力的支持。

名词解释第一章1.正应变是单位长度的伸缩变化量，亦称线应变；2.切应变一般指的是两个直线段间夹角的改变量，以角度变小的变化量为正，变大为负，以弧度表示。

3.主平面：切应力等于零的平面。

把此时该面上的正应力称作主应力。

4.平面应变状态：应变发生在同一个平面内。

5.胡克定律：在材料的线弹性范围内，固体的单向拉伸变形与所受的外力成正比。

6.应力集中：应力在局部增大的现象，一般出现在物体形状急剧变化的地方，如缺口、孔洞、沟槽以及有刚性的约束处。

7.理论应力集中因数：在材料的弹性范围内，最大局部应力与名义应力的比值；Kt=σmax σ8.应力状态软性系数:三个主应力可以按“最大切应力理论”计算最大切应力，按“相当最大正应力理论”计算最大正应力，而二者的比值表示他们的相对大小.第二章1.弹性模量E、比例极限Rp、弹性极限Re、上屈服强度Reh、下屈服强度Rel、抗拉强度Rm、断后伸长率A、断面收缩率Z（各定义的点以及公式）2.规定塑性延伸强度：拉伸中当试样的塑形伸长率等于L0的某一百分率时所对应的应力值；3.应变硬化指数：。

4.形变强化：屈服后的应力-应变曲线的上升被描述为形变强化（加工硬化）。

也就是随着应变的增加，材料的变形抗力增加5．静态韧性：在静载作用下，材料断裂前所吸收的能量，称作静态韧性，静态韧性可能包含三部分能量，即弹性变形能、塑性变形能和断裂能（形成两个断裂表面的能）。

6.静态韧度：静态韧度是表征静态韧性的力学性能指标，7.断裂强度：拉伸断裂时的真应力称为断裂强度，记为σf ；也有称为断裂真应力，记为Sk8.断裂延性：拉伸断裂后的真应变称为断裂延性，记为εf ，或称断裂真应变。

9.弹性比功：材料吸收变形功而又不发生永久变形的能力，也就是在开始塑性变形前，单位体积材料所能吸收的最大弹性变形功。

第三章1.比弹性模量：弹性模量与密度的比值；2.比刚度：刚度与密度的比值；3.弹性不完善性：应变不止与应力有关，还与时间和加载速率有关。