初三数学试题参考答案及评分标准

福田区2023-2024学年第二学期九年级中考适应性考试数学参考答案及评分标准二、填空题（每小题3分，共15分）（说明：填空题的结果不化简的不给分）三、解答题16. 解：原式= 1(3)42--+⨯…………4分（每个考点给1分） = . …………5分17. 解：原式=222(2)222(2)x xx x x--⎛⎫+⋅⎪---⎝⎭…………4分=222x xx-⋅-…………5分=2x. …………6分当x=4时，原式=42=2. …………7分18．解：（1）③④…………2分（对一个给1分，多选不给分）（2）事件①：第一天，丁考查B景点；事件②：第一天，戊考查A景点（合理即可给分）……………………4分（3）评价：①小明的解法不对．……………………5分②错误原因是：表格中列举的6种人员分布状态，并非6种等可能结果.丁、戊两名同学与景点的匹配关系，可能形成如下几种等可能结果列表法：丁A B CA AA AB ACB AB BB BCC AC BC CC戊………7分树状图法：说明：第（2）问的答案是开放的；第（3）问，采取开放性评价方式：能指出小明解法错误的，给1分，能正确指出错误原因的，另加2分，但本题总得分不得超过8分.19. 解：（1）设“K 牌甜筒”的进价为元/个，则“文创雪糕”的进价为（+1）元/个. 依题意得，…………1分80012001m m =+.…………2分 解得，=2. …………3分经检验，=2是原方程的解. …………4分 所以，+1=3.答：“K 牌甜筒”的进价为2元/个，“文创雪糕”的进价为3元/个. …………5分 （2）依题意得，(20200)(3)(20020200)(52)w x x x =-+-++--=220320600x x -+-. …………6分当＝32082(20)-=⨯-<10时，每天总利润最大. …………7分此时，20820040y =-⨯+=（个）， 200-40=160（个） …………8分 答：当文创雪糕销售单价为8元时，每天总利润最大.为获得最大利润，笑笑应购进40个“文创雪糕”，160个“K 牌甜筒”． …………8分20.（1）证明：方法1：如图1，∵ AB 是圆O 的直径， ∴ ∠ADB =90°.所有可能出现的结果：AA ，AB ，AC ，BA ，BB ，BC ，CA ，CB ，CC.A B C ABCABCABC开始………7分∵ CE ∥AD ，∴ ∠1=∠ADB =90°. ……………………………1分 ∵ D 为弧AC 的中点， ∴ ∠ABD =∠CBD .又， GB =GB ，∠1=∠BGC =90°.∴ △GBC ≌△GBE (ASA) ， ……………………………2分 ∴ EB =CB .又， ∠ABD =∠CBD ，DB =DB ，∴ △DCB ≌△DEB ， …………………………3分 ∴ DC =DE . …………………………4分方法2：证△GBC ≌△GBE (ASA)，同方法一 ……………………………2分 ∵ △GBC ≌△GBE ， ∴ GE=GC ，EB=CB ，∴ DB 垂直平分EC ， ……………………………3分 ∴ DE=DC. ……………………………4分 说明：直接由“角平分线与垂线合一”得“等腰”或“垂直平分线”的，建议扣1分. （2）如图2，连接OD ，OC ；OD 交EC 于点K .∵ 弧AC =弧BC ， ∴ ∠AOC =90°.又，D 为弧AC 的中点， ∴ ∠AOD =∠COD =45°. ∵ OD =OA ，∴ ∠ADO =∠DAO =245180︒-︒=67.5°. 同理可得， ∠ODC =∠OCD =245180︒-︒=67.5°. ∵ EC ∥AD ， ∴ ∠ADO =∠DKF =67.5° . ………………………………………………5分 ∵ DF 是圆O 的切线， ∴ OD ⊥DF ， ∴ ∠ODF =90°.∴ ∠FDC =∠ODF -∠ODC =22.5°，且∠F =22.5°， ∴ DC =CF ，∠DCE =45° . ………………………………………………6分图1图2由（1）知，DC =DE ， ∴ ∠DEC =∠DCE =45°.∴ △DCE 是等腰直角三角形. ∵ 弧AD 与弧CD 相等， ∴ CD =AD . ∵ AD =2，∴ AD =DE =DC =CF =2. …………………………………………7分在等腰直角三角形DCE 中， EC =22DE DC +=2，∴ EF =EC +CF =2+2. …………………………………………8分21．解：（1）如图3所示： …………………………………………2分（边界线，阴影区域各一分）（2） 填“等比性质”或“等比定理”或“比例的性质”均给分. ………………3分d z 800=…………………………………………5分（3）①抛物线解析式为40545012++-=x x y .…………………………………7分 或写成21(20)4850y x =--+. …………………………………7分解：如图4，M 刚好进入感应区时，05.01=d ，02=d ，此时05.021=-=d d d ，此时，1600005.0800==z （mm ）=16（m ）. 因CD =10 mm ，f =4 mm ，可得，OP 所在直线解析式为：x y 54-=，图3令y =16，得x =-20，即，P （-20，16）. 当M 经过点r O 的正上方时，视差02.0=d 此时，4000002.0800==z （mm ）=40（m ）， 即，抛物线与y 轴交点的坐标为（0，40）， 当d 减小到上述1d 的13时，z =31648⨯=（m ）， 之后d 开始变大，z 开始变小， 即，抛物线顶点的纵坐标为48.设抛物线解析式为)0(2≠++=a c bx ax y ， 将（-20，16），（0，40）等代入得，2164002040448.4a b c c ac b a ⎧⎪=-+⎪⎪=⎨⎪-⎪=⎪⎩，， 解得，145b =，2125b =-.因为，a <0，对称轴在y 轴右侧，所以，b ＞0.故，b =54， 此时，a =501-.所以，抛物线解析式为40545012++-=x x y . ② 易知，直线OD 的解析式为x y 54=， …………………………………8分得，2451440.505y x y x x ⎧=⎪⎪⎨⎪=-++⎪⎩，解得，1x =520，2x =520-（舍）此时，y =516.所以，物体M 刚好落入“盲区”时，距离基线的高度为516m. …………………9分图422．（1）D …………3分（2）①22x y +的最小值为40- …………4分 理由如下：如图5，连接BP ，BD .则，BD ==. ………………4分由（1）知，22222x y PD +=+， ………………5分 所以，当PD 最小时，22x y +最小， ………………5分 而，PD ≥BD -BP=2（等号成立时，点P 位于BD 上）.所以，22x y +的最小值为()2222+=40- ………………6分 ② x y -的最大值为 ………………8分 此时，PD的长为 ………………10分 略解：求x y -的最大值.解法1：如图6，把△ABP 绕点B 顺时针旋转90，得△CBE ，此时，x y EC PC PE -=-=≤.（等号成立时，P ，E ，C 三点共线，存在两种不同的位置情形，如图6-1，6-2所示)ECCC图5图6图6-1图6-2解法2：如图6-3，在AB ，BC 上分别取点M ，N ，使BM =BN =1，则易得△MBP ∽△PBA ，所以，12MP BP PA AB ==，所以，MP =1122PA x =，同理，1122PN PC y ==， 又MP PN -≤MN =P 在直线MN 与⊙B 的交点上），所以，x y -≤略解：求此时PD 的长.由（1）知，2224PD x y =+-解法1：如图6-1，在△EBC 中，EB =2，BC =4，45BEC ∠=，通过解斜三角形EBC ，可得 ，E C x ==，此时，PC y ==，在图6-2中，同理可得，PC y ==，EC x =，无论哪种情况，12xy ==.而，22224()24PD x y x y xy =+-=-+-， 把上述结果代入，得22212428PD =+⨯-=.所以，此时，PD =解法2：如图6-4，通过构造圆的两条割线，可得，△MCP ∽△ECN ，得，2612xy CP CE CM CN =⋅=⋅=⨯=，又，x y -=所以，222232x y x y xy +=-+=所以，222432428PD x y =+-=-=.所以，此时，PD =CNCC图6-4解法3：如图6-5，连接AC ，由旋转性质，可得AP EC ⊥，此时，222AP PC AC +=，即，(22232x y +==，所以，222432428PD x y =+-=-=.所以，此时，PD =解法4：如图6-6，连接BD ，交MN 于点F ，连接AC ，则BD AC ⊥，又易得MN ∥AC ，所以，BD MN ⊥，易得，BF =，DF = 当M ，N ，P 三点共线时，PF=，所以，PD ==CC图6-5。

房山区2023年初中学业水平考试模拟测试（一）九年级数学参考答案一、选择题（共16分，每题2分）二、填空题（共16分，每题2分）9.x≥5 10.a (x －1) 2 11.a+b 12.＜13.2914.答案不唯一，ac=4即可 15.李波 16. 5，14三、解答题（共68分，第17-20题，每题5分，第21题6分，第22题5分，第23-24题，每题6分，第25题5分，第26题6分，第27-28题，每题7分）17．()04sin 6043--++π-………………………………4分………………………………5分18. 解①得：x ＜3 ………………………………2分解②得：x ＞2………………………………4分∴不等式组的解集是2＜x ＜3 ………………………………5分19. 解： ………………………………2分………………………………3分………………………………4分………………………………5分441413=-++=-+=-982962)3()2(2222a a a a a a a a a 222430,43286=6+9=15a a a a a a +-=∴+=∴+=∴原式20. 方法一：证明：∵AD 平分∠BAC∴∠BAD =∠CAD ， ………………………………1分 在△BAD 与△CAD 中， ===AB ACBAD CAD AD AD ⎧⎪∠∠⎨⎪⎩∴△BAD ≌△CAD ………………………………3分 ∴BD =CD ，∠BDA =∠CDA ， ………………………………4分 ∵∠BDA+∠CDA=180°，∴∠BDA =∠CDA=90°∴AD ⊥BC ………………………………5分 方法二：证明：∵点D 为BC 中点，∴BD =CD ， ………………………………1分 在△BAD 与△CAD 中， ===AB AC AD AD BD CD ⎧⎪⎨⎪⎩，，∴△BAD ≌△CAD ………………………………3分 ∴∠BAD =∠CAD ，∠BDA =∠CDA ， ……………………4分又∵∠BDA+∠CDA=180°， ∴∠BDA =∠CDA=90°∴AD ⊥BC ………………………………5分 方法三：证明：∵AB=AC∴∠B =∠C ………………………………1分 ∵AD ⊥BC ，∴∠BDA =∠CDA=90° ………………………………2分 在△BAD 与△CAD 中，DCBAD CB AABCD===AB AC AD AD BD CD ⎧⎪⎨⎪⎩，， ∴△BAD ≌△CAD ………………………………4分 ∴BD =CD ，∠BAD =∠CAD . ………………………………5分（其它证法酌情给分）21.（1） 证明：∵ ABCD 中，对角线AC 、BD 交于点O ，∴OA =OC ， ………………………………1分 又∵OE=OF=OA ，∴四边形AECF 是平行四边形， ……………………2分 ∵ OE=OF=OA=OC ， ∴OE+OF=OA+OC ， 即AC =EF ，∴ AECF 是矩形. ………………………………3分（2）证明：∵四边形AECF 是矩形且AE=AF ，∴四边形AECF 是正方形， …………………………4分 ∴AC ⊥EF ，∴ ABCD 是菱形， …………………………5分 ∴AC 平分∠BAD . …………………………6分（其它证法酌情给分）22.（1）解：∵点A （1，a ）在直线y = kx+ 3k （k >0）上，∴a = k +3k =3 ………………………………1分即a 值为3∵直线y = x + m 经过点B （2，3），∴2+m =3，∴m =1. ………………………………2分 ∴直线2l 的表达式为y = x + 1 . ……………………3分 （2）k 的取值范围为1≤k ≤23. ………………………………5分23.（1）证明：连接AO ， ……………………1分∵AB =AC ，点O 为直径BC 中点，∴AO ⊥BC ，∠BAC =2∠OAC ， ……………………2分 ∴∠OAC +∠ACO =90°， ∵BC 为⊙O 直径，点D 在⊙O 上， ∴∠BDC =90°， ∴∠DBC +∠ACO =90°， ∴∠DBC =∠OAC ，∴∠BAC =2∠DBC ； ……………………3分（2）解：连接OD ， ……………………4分 ∴∠DOE =2∠DBC ， 又∵∠BAC =2∠DBC ，∴∠BAC=∠DOE ， ……………………5分∴cos ∠DOE = cos ∠BAC =53，∵DE 切⊙O 于点D ， ∴∠ODE =90°， 在Rt △ODE 中，cos ∠DOE =OD OE =53，∴设OD =3x ，OE =5x ， ∴由勾股定理可得，DE =4x ， ∵DE =4， ∴4x =4， ∴x =1，∴OE =5，OD =3，∴OB =OD =3，∴BE =OB +OE =3+5=8. ……………………6分 （其它解法酌情给分）24. （1）74 ……………………2分（2）甲校 ……………………4分 （3）答案不唯一 ……………………6分25. （1）“门高”： 7.2 m ……………………1分设函数表达式2(6)7.2y a x =-+ （a ＜0） ……………………2分 将点（12，0）代入得：367.20a +=，解得0.2a =-，故拱门上的点满足的函数关系为：20.267.2y x =--+（）. …………………3分（2） ＞ ……………………5分26.（1）把（1,1）代入表达式得，112a b =-+，∴a b 2= ……………………1分 抛物线为22222()2y x ax a x a a a =-+=--+抛物线顶点坐标为2(,2)a a a -+ ……………………2分（2）∵抛物线关于x =a 对称，开口向上，∴当1-a ≤x ≤2+a 时，由对称性得，x =2+a 时函数y 有最大值： y 最大=(a+2－a )2－a 2+2a=－a 2+2a+4. ……………………3分 ∵对于任意1-a ≤x ≤2+a ,都有y ≤1，∴－a 2+2a+4≤1 ……………………4分 即a 2－2a －3≥0∴ a ≤－1或a ≥3 ……………………6分 （其它解法酌情给分）27.（1）补完图形如下：……………………1分∠ADG =∠CDG . ……………………2分证明：如图，连接AG 、CG∵∠EAF =90° ，点G 是EF 中点，∴AG =12EF∵正方形ABCD ，∠ECF =90° ，∴CG =12EF∴AG =CG ……………………3分 ∵AD =CD ，DG =DG ∴△ADG ≌△CDG∴∠CDG =∠ADG ……………………4分 （2）BC =3BE ……………………5分过点G 作GH ⊥CD 于点H ， 易证GH 是△CEF 的中位线，∴CE =2GH . ……………………6分 易证△GDH 是等腰直角三角形，∴DG .又∵DG DF ，∴DF =GH . 易证△ADF ≌△ABE ∴DF =BE ， ∴BE =GH . ∵CE =2GH ， ∴CE =2BE∴BC =3BE ……………………7分 （其它证法酌情给分）28.（1）①（－2，1）； ……………………2分②存在.设点B 坐标为（x ，x －1），则它向右平移1个单位，再向下平移1个单位 的点坐标为B'（x +1，x －2），B'关于y 轴对称点坐标为（－x －1，x －2） ……………3分 代入y = x －1得x －2 =－x －1－1，x = 0； ……………………4分 ∴点B 坐标为（0，－1）. ……………………5分（2）－12 ≤t ≤12 ……………………7分。

1 - 4 4 O20 7九年级数学参考答案及评分标准一、选择题（本大题共12个小题.1-6小题，每小题2分，7 — 12小题，每小题3分，共30分）1.B2.D3. C4.A5. A6. B7. C8. C9. C 10. C 11. A 12. D二、填空题（每小题3分，共18分）三、解答题（本大题共8个小题，共72分）以下解答部分过程部分省略19、（本小题满分8分）6 ------------------------------------------------ （8 分）20、（本小题满分8分）解（1）由题意，有= 解得m=l. ..................................................... （3 分）2（2）如图1；（5分）图1 图2（3）如图2, xW— 2 或....................... （8 分）21、（本小题满分8分）（1）........................................................................... —. （3 分）13（2）解：如图,连接BC.9：AB为。

O的直径，..・ZACB=90°.「•由（1）知AC= 13^ AE = \2 cos A 12 13 在RtAACB 中，cosX = —AB."眼竺……1225/• BE = AB — AE（8 22、（本小题满分8（1）0.4 （4分）（2）0.6 （8分）23.（本小题满分9分）（1）证明：如图1连结ADBD = CD:.AD _ BC.又・.・L43C=45°:.BD =.4B cosZ-45C................................. 2分△ABE =匕DB\1:AABE^ADBM ................................................ 4 分DM DB:.AE = 0n） .............................................. 6 分（2）AE =2MD24.（本小题满分9分）cA B （6分）D图1（1）证明：I弦CDL直径48于点E,.・.宏=-矽・・.・ ZACD=ZAFC.又•「ZCAH=ZFAC,（3分）(2)猜想：AH • AF=AE • AB.证明：连结FB.•.・AB为直径，二ZAFB=90° .又•「ABLCD于点E,・.・ZAEH=9Q° ./. ZAEH = ZAFB . ZEAH=ZFAB,:.4AHEs 4ABF.・・・ AH ^AF=AE (6分)（3）答：当点E位于。

张卡片，除所标注文字不同外无其他差别．其中，写有“珍稀濒危植．随机摸出一张卡片写有“珍的扇形作圆锥的侧面，记扇形的半径为R，所在一定范围内变化时，l与S都随R的变第12题图第14题图试题13．某科技公司开展技术研发，在相同条件下，对运用新技术生产的一批产品的合格率进行检测，下表是检测过程中的一组统计数据：估计这批产品合格的产品的概率为．14．如图，AB 是半圆O 的直径，将半圆O 绕点A 逆时针旋转30°，点B 的对应点为B '，连接A B '，若AB ＝8，则图中阴影部分的面积是_______.15．对于向上抛的物体，在没有空气阻力的条件下，上升高度h ，初速度v ，抛出后所经历的时间t ，这三个量之间有如下关系：221gt vt h -=（其中 g 是重力加速度，g 取10m/s 2）．将一物体以v=21m/s 的初速度v 向上抛，当物体处在离抛出点18m 高的地方时，t 的值为 ．16．已知函数y 1＝kx ＋4k －2（k 是常数，k ≠0），y 2＝ax 2＋4ax －5a （a 是常数，a ≠0），在同一平面直角坐标系中，若无论k 为何值，函数y 1和y 2的图象总有公共点，则a 的取值范围是_______.三、解答题（共68分，第17-22题，每题5分，第23-26题，每题6分，27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程．17．解方程x 2-1 =6x ．18．关于x 的一元二次方程x 2-(m +4)x +3(m +1)=0 ．（1）求证：该方程总有两个实数根；（2）若该方程有一根小于0，求m 的取值范围．抽取的产品数n 5001000150020002500300035004000合格的产品数m 476967143119262395288333673836合格的产品频率nm0.9520.9670.9540.9630.9580.9610.9620.959图2图3图1图1 图2试题北京市朝阳区2023～2024学年度第一学期期末检测九年级数学试卷参考答案及评分标准(选用)2024.1一、选择题（共16分，每题2分）题号12345678答案DABCACAC二、填空题（共16分，每题2分）三、解答题（共68分，第17-22题，每题5分，第23-26题，每题6分，27-28题，每题7分）17．解：方程化为x 2 -6x =1．x 2 -6x+9 =10．1032=-）（x ．103±=-x ．1031+=x ，1032-=x ．18．（1）证明:依题意，得=[-(m +4)]2-4×3(m +1) =(m -2)2．∵(m -2)2≥0，∴0≥∆∴该方程总有两个实数根．（2）解：解方程，得x =．∴x 1= m +1，x 2=3．依题意，得m +1<0．∴m <-1．19．解：（1）根据题意，设该二次函数的解析式为 y 2=a (x -1)2+4．当x =0时，y 2 =3∴a =-1．∴y 2=-x 2+2x +3．题号9101112答案x 1=3，x 2=-3相切（1，3）140题号13141516答案答案不唯一，如0.9593438+π1.2或3a ＜0或a ≥52线段垂直平分线上的点与这条线段两个端点的距离相等.三角形的外角等于与它不相邻的两个内角的和.由题意可知，抛物线顶点C ），（9254．设抛物线对应的函数解析式)4(2+-=x a y试题26. 解：（1）由题意知，a +b +c = 9a +3b +c .∴b = -4a .∴22=-=a b t . （2）∵a >0，∴当x ≥t 时，y 随x 的增大而增大；当x ≤t 时，y 随x 的增大而减小.设抛物线上的四个点的坐标为A (t -1，m A ) ，B （t ，m B ），C （2，n C ），D （3，n D ）.点A 关于对称轴x =t 的对称点为A'（t +1，m A ）∵抛物线开口向上，点B 是抛物线顶点，∴m A ＞m B .ⅰ 当t ≤1时，n C < n D∴t +1≤2.∴m A ≤n C ，∴不存在m ＞n ，不符合题意.ⅱ 当1<t ≤2时，n C < n D∴2<t ＋1≤3.∴m A ＞n C .∴存在m ＞n ，符合题意.ⅲ当2<t ≤3时，∴n 的最小值为m B .∵m A ＞m B .. ∴存在m ＞n ，符合题意.ⅳ 当3<t <4时，n D <n C .∴2<t －1＜3.∴m A ＞n D .∴存在m ＞n ，符合题意.ⅴ 当t ≥4时，n D <n C .∴t -1≥3.∴m A ≤n D ，∴不存在m ＞n ，不符合题意.综上所述，t 的取值范围是1<t <4.）解：补全图1，如图.证明：延长AF到点G，使得GF=AF，连接，连接GE并延长，与AB的延长。

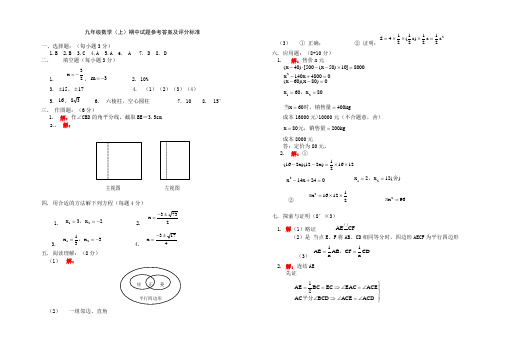
九年级数学（上）期中试题参考答案及评分标准一、选择题：（每小题3分）1.B2.B3.C4.A5.A6. A7. D8. D二、 填空题（每小题3分）1.x =-32，m =-3 2. 10%3. ±15，±174. （1）（2）（3）（4）5. 16，836. 六棱柱，空心圆柱7. 108. 15°三、 作图题：（6分）1. 解：作∠CBD 的角平分线，截取BE ＝3.5cm2.. 解：主视图左视图四. 用合适的方法解下列方程（每题4分）1. x x 1232==-，2.x =-±37323.x x 12133==-， 4.x =-±3174 五. 阅读理解：（8分）（1） 解：矩 正 菱平行四边形（2） 一组邻边、直角（3） ① 正确； ② 证明：S a a a =⨯⨯⨯=4121212122()六. 应用题：（8+10分） 1. 解：售价x 元()[500()]x x -⋅--⨯=4050108000x x 214048000-+= ()()x x --=60800x x 126080==，当时，销售量x kg ==60400成本16000元>10000元（不合题意，舍） x kg ==80200元，销售量 成本8000元答：定价为80元。

2. 解：①()()162122121612--=⨯⨯x xx x 214240-+= x x 12212==，舍()②πx 2161212=⨯⨯πx 296=七. 探索与证明（8’×3）1. 解（1）略证 AE CF //（2）是 当点E 、F 将AB 、CD 相同等分时，四边形AECF 为平行四边形 （3）AE n AB CF n CD ==11，2. 解：连结AE 先证AE BC EC EAC ACE AC BCD ACE ACD ==⇒∠=∠∠⇒∠=∠⎫⎬⎪⎭⎪12平分⇒∠=∠⇒⎫⎬⎭⇒=⎫⎬⎪⎭⎪⇒EAC ACD AE DC AD BC AECD AE EC AECD ////为平行四边形为菱形3.解：已知：中，，∆ABC BC AB ACB =∠=1290ο求证：∠=BAC 30οD C B证明 延长BC 至D ，使BC ＝CD Θο∠=ACB 90∴∠=ACD 90ο在和中∆A ∆A CD BCAC AC ACD ACB DC BC =∠=∠=⎧⎨⎪⎩⎪∴≅∆∆ACD ABC九年级数学（上）期中试题命题说明一、 命题意图为了使学生能够更好掌握本学期前四章所学知识的运用能力，分析能力，判断能力，加强基础知识的练习，激发学生的学习兴趣，按 照教学大纲的要求来命题的。

南安市2023—2024学年度上学期期末教学质量监测初三数学参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分．（二）如解答的某一步出现错误，这一步没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分．（三）以下解答各行右端所注分数表示正确做完该步应得的累计分数．（四）评分最小单位是1分，得分或扣分都不出现小数．一、选择题（每小题4分，共40分）1．A ；2．C ；3．C ；4．B ；5．B ；6．A ；7．B ；8．D ；9．C ；10．B ．二、填空题（每小题4分，共24分）11；12．2024；13．60；14．14；15；16．①③④16．解：∵△BPC 是等边三角形，四边形ABCD 是正方形，∴60PCB CPB ∠=∠=︒，30PCD ∠=︒，CB PC CD ==，∴75CPD CDP ∠=∠=︒，则6075135BPD ∠=︒+︒=︒，∵45CBD CDB ∠=∠=︒，∴135DBH DPB ∠=∠=︒，∵PDB BDH ∠=∠，∴△BDP ∽△HDB ，故①正确；如图，过点Q 作QE CD ⊥于E ，设QE DE x ==，则QD =，22CQ QE x ==，∴CE =，由CE DE CD +=知2x =，解得1x -，∴DQ =，∵BD =∴BQ BD DQ =-=-=，故②错误；∵304575DQP PCD CDB DPC ∠=∠+∠=︒+︒=︒=∠，∴DP DQ=故③正确；DP DQ ==∴111sin 1222BDP S BD DP BDP ∆=⋅⋅∠=⨯⨯=-，故④正确；故答案为：①③④．三、解答题（共86分）17．（本题8分）计算÷解：原式＝-……………………………………………6分＝-……………………………………………8分18．（本题8分）2210x x +-=解：221x x +=……………………………………………2分2(1)2x +=……………………………………………4分1x +=……………………………………………6分11x =-+21x =--…………………………………………8分19．（本题8分）如图，点O 为所要画的点.……………………………4分如图，△11A B C 为所要画的三角形.…………………………8分20．（本题8分）解：设该市这两年平均每年种植面积增长的百分率是x ，……………1分由题意得：210(1)12.1x +=………………………………………4分整理得：2(1) 1.21x +=………………………………………5分解得：10.1x =或2 2.1x =-（不符合题意，舍去），……………7分∴0.1x ==10%答：该市这两年平均每年种植面积增长的百分率是10%．……8分21．（本题8分）解：（1）12．…………………………………………3分（2）根据题意画树状图如下：……6分共有6种机会均等的结果；其中在寻宝游戏中胜出的有1种,…7分则寻宝游戏中胜出的概率是16．………………………………8分22．（本题10分）解：（1）是………………………………3分（2）∵一元二次方程20(0)ax c a+=≠是倍根方程，∴设方程的两根分别为t，2t，根据根与系数的关系得 (4)分32t ta+=-=2ct ta⋅=，……………………………8分∴33t=，………………………………9分∴2322()33ca=⨯=．………………………………10分23．（本题10分）解：（1）如图，过点B作BE OC⊥于点E，……………………1分在Rt ABE∆中，53BAC∠=︒，3AB=m，∴412sin355BE AB BAC=⋅∠≈⨯=（m），……………………2分在Rt BOE∆中，37BOE∠=︒，125BE≈m，∴12543sin375BEOB=≈=︒（m）…………………………4分答：OB的长约为4m；（2）如图，过点D作DF OC⊥于点F，旋转后点D的对应点为点D′，过点D′作'D G OC⊥于点G，过点D作'DH D G⊥于点H，…5分在Rt FOD∆中，4610OD OB BD=+≈+=m，37DOF∠=︒，∴3sin371065DF OD=⋅︒≈⨯=（m），…………………………6分∴'D G≈3+6＝9（m），…………………………7分在Rt'D OG∆中，'10OD≈m，'D G≈9m，∴9sin 10D'OG ∠≈，…………………………8分∴'64D OG ∠≈︒，…………………………9分∴'643727D OD ∠≈︒-︒=︒，即云梯OD 大约旋转了27°．…………………………10分24．（本题12分）（1）证明：如图所示，∵四边形ABCD 是菱形∴1122ACB ACD BCD BAD ∠=∠=∠=∠…………………………1分∵12MAN BAD∠=∠∴MAN ACB ACD ∠=∠=∠∴1224∠+∠=∠+∠∴14∠=∠…………………………2分同理，23∠=∠………………………3分∴△ACF ∽△ECA ∴AC CFEC AC=…………………………4分∴2AC EC CF=⋅……………………5分（2）过点F 作FG BC ⊥于点G ，过点A 作AH BC ⊥于点H ………6分∵四边形ABCD 是菱形∴AB BC m ==，AB ∥CD ……………………………7分∴5B ∠=∠……………………………………………8分∵12ECF S EC FG ∆=⋅,Rt CFG ∆中，sin 5FG CF =⋅∠∴ECF S ∆1sin 52EC CF =⋅⋅∠由（1）知2AC EC CF =⋅∴21sin 52ECF S AC ∆=∠21sin 2n B =………10分∵12ABCS BC AH ∆=⋅,Rt ABH ∆中，sinB AH AB =⋅∴ABC S ∆1sin 2BC AB B =⋅⋅21sin 2m B =∴22221sin 21sin 2ECF ABCn BS n x S m m B ∆∆===………………………12分25．（本题14分）（1）解：解方程223x x -=得13x =或21x =-………………………………1分∵0k >∴3k =∴正比例函数为3y x=………………………………2分由34y x y x =⎧⎨=-+⎩得13x y =⎧⎨=⎩图2∴点A 的坐标为(1，3)………………………………3分（2）解：令0y =，则40x -+=得4x =∴点B 的坐标为(4，0)………………………………4分过点A 作AD OB ⊥于点D ，过点O 作OP AB ⊥于点P则3AD =，如图1在Rt OAD ∆中，1OD =，3AD =,在Rt ABD ∆中，3AD =，413BD =-=223110OA =+=，223332AB =+=…………5分∵1122AOB S OB AD AB OP∆=⋅=⋅∴432232OP ⨯==……………6分∴2225sin 510OP OAB OA ∠===……7分（3）解：直线AB 上存在一点C ，使得2tan 3AOC ∠=，分两种情况讨论：………………………8分①当点C 在点A 下方时，过点A 作AE y ⊥轴于点E ，延长EA 到点F ，使得2AF =过点F 作FG AF ⊥交OA 的垂线于点G ，连结OG ,OG 与AB 的交点为点C （如图2），理由如下………………………9分∵AG OA ⊥∴1290∠+∠=︒图1∵AE y ⊥轴∴1390∠+∠=︒∴23∠=∠∵90AFG AEO ∠=∠=︒∴△GFA ∽△AEO∴AF GF AGOE AE OA==∴22133AF GF AE OE =⋅=⨯=，在Rt AOG∆2tan =3AG AOC OA ∠=∴点G 的坐标为(3，73)…………………………10分求得直线OG 的函数解析式为79y x =由794y x y x ⎧=⎪⎨⎪=-+⎩得9474x y ⎧=⎪⎪⎨⎪=⎪⎩∴点C 的坐标为(94，74)…………………………11分②当点C 在点A 上方时，将△AFG 绕点A 旋转180︒后得到△ANM ，则△AFG ≌△ANM ，且AM OA ⊥，直线OM 与直线4y x =-+的交点C'为所求的点．（如图3）………………………………………12分由①知△GFA ∽△AEO ∴△ANM ∽△OEA∴23AM AN AF OA OE OE ===∴在Rt AOM ∆中2tan =3AM AOC OA ∠=‵∴223AN AF ,MN FG ====∴点M 的坐标为(1-，113)求得直线OM 的函数解析式为113y x =-…………………13分由1134y x y x ⎧=-⎪⎨⎪=-+⎩得32112x y ⎧=-⎪⎪⎨⎪=⎪⎩∴点C'的坐标为(32-，112)综上所述，直线AB 存在一点(94，74)或(32-，112)，使得2tan 3AOC ∠=．…………………………14分图3。

第一学期期末九年级数学参考答案及评分标准一、选择题（每小题3分，共36分）BCBAD ACBCD DA二、填空题（每小题3分，共12分）13．0.9； 14． 4 ； 15． 8 ； 16．222- 三、解答题17．解：原式 =()22232⨯- ……………………2分（每写对一个函数值得1分） = 3–1 ………………………………… 4分（每算对一个运算得1分） = 2 …………………………………… 5 分18．解法一：移项得 342-=-x x ……………………1分 配方得 43442+-=+-x x()122=-x ……………………2分即 12=-x 或12-=-x ………3分 ∴31=x ，12=x …………………5分解法二：∵1=a ，4-=b ，3=c∴()043144422>=⨯⨯--=-ac b ……………………1分∴()224244±=±--=x ……………………………………3分∴31=x ，12=x ………………………………………………5分解法三：原方程可化为 ()()031=--x x …………………… 1分 ∴x –1 = 0或x –3 = 0 …………………………… 3分 ∴11=x ，32=x ………………………………… 5分 19．（1）证明：∵DE ⊥AB ，AB//CD∴DE ⊥CD ∴∠1+∠3=90º ………………1分 ∵BD ⊥AD ∴∠2+∠3=90º∴∠1=∠2 …………………… 2分 ∵CF ⊥BD ，DE ⊥AB ∴∠CFD=∠AED=90º ……………… 3分 ∵AD=CD∴△ADE ≌△CDF …………………… 4分（2）解：∵DE ⊥AB ，AE=2，AD=4∴∠2=30º，DE=32242222=-=-AE AD ……………… 5分 ∴∠3=90º–∠2=60º ∵△ADE ≌△CDF∴DE=DF ………………………………………………………… 6分 ∴△DEF 是等边三角形∴EF=DF=32…………………………………………………… 7分 （注：用其它方法解答的，请根据此标准酌情给分）ADBC EF图912 320．（1）31…………………………………………2分 （2）解：列表得结果共有9种可能，其中能成紫色的有2种∴P （获胜）=92（说明：第（2）小题中，列表可画树状图得4分，求出概率得2分，共6分） 21．（1）解：过点C 作CD ⊥l 1于点D ，则已知得 ………………………… 1分 AC=3×80=240（km ），∠CAD=30º ………………………… 2分 ∴CD=21AC=21×240=120（km ）…………………………3分∴C 市到高速公路l 1的最短距离是（2）解：由已知得∠CBD=60º 在Rt △CBD 中， ∵sin ∠CBD=BCCD∴BC=38060sin 120sin =︒=∠CBD CD ………………………………5分∵∠ACB=∠CBD –∠CAB=60º–30º=30º∴∠ACB=∠CAB=30º∴AB=BC=380…………………………………………………………6分 ∴t =5.3732.12328038038080≈⨯≈=+=+BC AB ………………7分答：经过约3.5小时后，他能回到A 市。

初三数学试卷第1页(共6页)大兴区2023~2024学年度第一学期期末检测初三数学2024.01考生须知1.本试卷共6页,共三道大题,28道小题,满分100分,考试时间120分钟㊂2.在答题卡上准确填写学校名称㊁准考证号,并将条形码贴在指定区域㊂3.题目答案一律填涂或书写在答题卡上,在试卷上作答无效㊂4.在答题卡上,选择题㊁作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答㊂5.考试结束,请将答题卡交回㊂一㊁选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.2023航空航天大兴论坛于11月15日至17日在北京大兴国际机场临空经济区举办,共设置了数字民航 电动航空 商业航天 通航维修 四场专题论坛.若某位航天科研工作者随机选择一个专题论坛参与活动,则他选中 电动航空 的概率是A.1B.12C.14D.182.下列图形中,是中心对称图形而不是轴对称图形的为㊀㊀A.㊀ B.㊀C.㊀D.3.关于一元二次方程x 2-3x -1=0的根的情况,下列说法正确的是A.有两个不相等的实数根 B.有两个相等的实数根C.没有实数根D.无法判断4.抛物线y =(x -2)2+1的对称轴是A.x =-2B.x =2C.x =-1D.x =15.在平面直角坐标系xOy 中,将抛物线y =3x 2先向右平移4个单位长度,再向上平移1个单位长度,得到的抛物线是A.y =3(x +4)2-1B.y =3(x +4)2+1C.y =3(x -4)2-1D.y =3(x -4)2+1初三数学试卷第2页(共6页)6.若圆的半径为1,则60ʎ的圆心角所对的弧长为A.π2B.πC.π6D.π37.如图,菱形OABC 的顶点A ,B ,C 在☉O 上,过点B 作☉O 的切线交OA 的延长线于点D.若☉O 的半径为2,则BD 的长为A.2 B.22C.23D.48.如图,点A ,B 在☉O 上,且点A ,O ,B 不在同一条直线上,点P 是☉O 上一个动点(点P 不与点A ,B 重合),在点P 运动的过程中,有如下四个结论:①恰好存在一点P ,使得øPAB =90ʎ;②若直线OP 垂直于AB ,则øOAP =øOBP ;③øAPB 的大小始终不变.上述结论中,所有∙∙正确结论的序号是A.①②B.①③C.②③D.①②③二㊁填空题(共16分,每题2分)9.若(a -3)x 2-3x -4=0是关于x 的一元二次方程,则a 的取值范围是.10.若关于x 的一元二次方程x 2-3x +m =0有一个根为1,则m 的值为.11.在平面直角坐标系xOy 中,若点(2,y 1),(4,y 2)在抛物线y =2(x -3)2-4上,则y 1y 2(填 > , = 或 < ).12.如图,四边形ABCD 内接于☉O ,点E 在AD 的延长线上,若øCDE =80ʎ,则øABC 的度数是ʎ.13.如图,әABC 的内切圆☉O 与AB ,BC ,CA 分别相切于点D ,E ,F ,若AD =2,BC =6,则әABC 的周长为.初三数学试卷第3页(共6页)14.写出一个过点(0,1)且当自变量x >0时,函数值y 随x 的增大而增大的二次函数的解析式.15.杭州亚运会的吉祥物 琮琮 宸宸 莲莲 组合名为 江南忆 ,出自唐朝诗人白居易的名句 江南忆,最忆是杭州 ,它融合了杭州的历史人文㊁自然生态和创新基因.吉祥物一开售,就深受大家的喜爱.经统计,某商店吉祥物 江南忆 6月份的销售量为1200件,8月份的销售量为1452件,设吉祥物 江南忆 6月份到8月份销售量的月平均增长率为x ,则可列方程为.16.如图,在平面直角坐标系xOy 中,二次函数y =ax 2+bx +c (a(2,1).给出下面三个结论:①2a -b =0;②a +b +c >1;③关于x 的一元二次方程ax 2+bx +c -m =0(m <1)有两个异号实数根.上述结论中,所有正确结论的序号是.三㊁解答题(共68分,第17-21题每题5分,第22题6分,第23题5分,第24-26题每题6分,第27-28题,每题7分)解答应写出文字说明㊁演算步骤或证明的过程.17.解方程:x 2+8x =9.18.已知a 是方程x 2-2x -1=0的一个根,求代数式(a -1)2+a (a -2)的值.19.已知关于x 的一元二次方程x 2-x +2m -2=0有两个实数根.(1)求m 的取值范围;(2)当m 取最大整数值时,求方程的根.20.已知抛物线y =x 2+bx +c 经过点(1,0),(0,-3).(1)求抛物线的解析式;(2)求该抛物线的顶点坐标.21.如图,在әABC 中,øC =45ʎ,AB =2,☉O 为әABC 的外接圆,求☉O 的半径.22.2023年9月23日至10月8日,第19届亚运会在杭州举行.中国队以201枚金牌㊁111枚银牌㊁71枚铜牌的优异成绩,位居奖牌榜首.为弘扬体育运动精神,某校对八㊁九年级学生进行了杭州亚运会知识竞赛(测试满分为100分,得分x均为不小于80的整数),并从其中分别随机抽取了20名学生的测试成绩,整理㊁描述和分析如下(成绩得分用x表示,共分成四组:A.80ɤx<85;B.85ɤx<90;C.90ɤx<95;D.95ɤxɤ100).a.八年级20名学生的成绩是:80,82,83,83,85,85,86,87,89,90,90,91,94,95,95,95,95,96,99,100.b.九年级20名学生的成绩在C组中的数据是:90,90,91,92,92,93,93,94.c.八㊁九年级抽取的学生竞赛成绩的平均数㊁中位数㊁众数如下:年级平均数中位数众数八年级9090m九年级90n100d.九年级抽取的学生竞赛成绩扇形统计图如下:根据以上信息,解答下列问题:(1)写出表中m,n的值及九年级抽取的学生竞赛成绩在D组的人数;(2)若该校九年级共400人参加了此次知识竞赛活动,估计九年级竞赛成绩不低于90分的人数是;(3)为了进一步弘扬体育运动精神,学校决定组织学生开展亚运精神宣讲活动,准备从九年级抽取的竞赛成绩在D组的学生中,随机选取一名担任宣讲员,另一名担任主持人.若甲㊁乙是抽取的成绩在D组的两名学生,用画树状图或列表的方法,求甲㊁乙两人同时被选上的概率.初三数学试卷第4页(共6页)初三数学试卷第5页(共6页)23.在平面直角坐标系xOy 中,函数y =kx +b (k ʂ0)的图象经过点A (-1,2)和B (1,4).(1)求该函数的解析式;(2)当x >2时,对于x 的每一个值,函数y =12x +n 的值小于函数y =kx +b (k ʂ0)的值且大于5,直接写出n 的值.24.如图,AB 是☉O 的直径,点C 在☉O 上,连接AC ,BC ,过点O 作OD ʅBC 于点D ,过点C作直线CE 交OD 延长线于点E ,使得øE =øB.(1)求证:CE 为☉O 的切线;(2)若DE =6,CE =35,求OD 的长.25.如图1,某公园一个圆形喷水池,在喷水池中心O 处竖直安装一根高度为1.25m 的水管OA ,A 处是喷头,喷出水流沿形状相同的曲线向各个方向落下,喷出水流的运动路线可以看作是抛物线的一部分.建立如图2所示的平面直角坐标系,测得喷出水流距离喷水池中心O 的最远水平距离OB 为2.5m,水流竖直高度的最高处位置C 距离喷水池中心O 的水平距离OD 为1m.(1)求喷出水流的竖直高度y (m)与距离水池中心O 的水平距离x (m)之间的关系式,并求水流最大竖直高度CD 的长;(2)安装师傅调试时发现,喷头竖直上下移动时,抛物线形水流随之竖直上下移动(假设抛物线水流移动时,保持对称轴及形状不变),若水管OA 的高度增加0.64m 时,则水流离喷水池中心O 的最远水平距离为m.初三数学试卷第6页(共6页)26.在平面直角坐标系xOy 中,点(2,m )在抛物线y =ax 2+bx +c (a >0)上,设抛物线的对称轴为x =t.(1)当m =c 时,求t 的值;(2)点(-1,y 1),(3,y 2)在抛物线上,若c <m ,请比较y 1,y 2的大小,并说明理由.27.在әABC 中,øBAC =90ʎ,AB =AC ,点P 为BA 的延长线上一点,线段PC 顺时针旋转90ʎ得到线段PD ,连接BD.(1)依题意补全图形;(2)求证:øACP =øDPB ;(3)用等式表示线段BC ,BP ,BD 之间的数量关系,并证明.28.如图,在平面直角坐标系xOy 中,已知点M (0,t ),N (0,t +2),对于坐标平面内的一点P ,给出如下定义:若øMPN =30ʎ,则称点P 为线段MN 的 亲近点 .(1)当t =0时,①在点A (23,0),B (3,2),C (-23,2),D (-1,-3)中,线段MN 的 亲近点 的是;②点P 在直线y =1上,若点P 为线段MN 的 亲近点,则点P 的坐标为;(2)若直线y =-3x -3上总存在线段MN 的 亲近点 ,则t 的取值范围是.大兴区2023~2024学年度第一学期期末检测初三数学参考答案及评分标准一、选择题（共16分，每题2分）二、填空题（共16分，每题2分）三、解答题（共68分，第17-21题每题5分，第22题6分，第23题5分，第24-26题每题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明的过程.17. 解： x 2+8x =9.x 2+8x +16=9+16. ··································································· 1分(x +4)2=25. ………………………………………………………………2分x +4=±5. ············································································· 3分 解得x 1=1，x 2=-9. ································································ 5分18. 解： 2(1)(2)a a a −+−=22212a a a a −++− ····························································· 2分 =2241a a −+ ········································································ 3分 ∵a 是方程2210x x −−=的一个根，∴2210a a −−=，∴221a a −=． ······································································· 4分∴原式2221a a =+（-）211=⨯+=3 ·············································································· 5分19. 解：（1）∵方程有两个实数根，0∴∆≥ ················································································· 1分∵Δ＝(－1) 2－4×1×(2m －2)188m =−+ 98m =− 980m ∴−≥98m ∴≤ ················································································ 2分（2）98m ≤，m 为最大整数，m ∴=1. ··············································································· 3分∴x 2﹣x ＝0.解得：x 1=0，x 2=1. ································································ 5分 20.解：（1）∵抛物线2+y x bx c =+经过点（1，0），（0，-3），∴1+03b c c +=⎧⎨=−⎩.··········································································2分解得2-3b c =⎧⎨=⎩.∴22-3y x x =+． ·····································································3分 （2）y =22-3x x +.()21-4x =+∴顶点坐标为（-1，-4）. ··························································· 5分21. 解：连接OA ，OB ，············································1分∵∠C ＝45°,∴∠AOB ＝2∠C =90°. ··········································2分 在Rt △AOB 中，∵OA 2+OB 2=AB 2, AB =2，OA =OB ，∴2 OA 2=4. ························································4分 ∴ OA 2=2.∴OA （舍负）.∴⊙O . ···········································5分 22.解：（1）m ＝95，n ＝90.5，九年级抽取的学生竞赛成绩在D 组的人数为4人； ···· 3分 （2）240. ····················································································· 4分 （3）设D 组的另外两名同学为丙，丁.宣讲员 甲 乙 丙 丁主持人 乙 丙 丁 甲 丙 丁 甲 乙 丁 甲 乙 丙由树状图可以看出，所有可能出现的结果共12种，这些结果出现的可能性相等． 甲和乙同时被选上的结果有2种， 所以P （甲乙同时被选上）=21126=． ································································ 6分23. 解：（1）把A （-1,2）和B （1,4）代入y=kx+b(k ≠0)中，24k b ,k b .−+=⎧⎨+=⎩………………………………………………………………1分解得：13k ,b .=⎧⎨=⎩………………………………………………………………2分 所以该函数的解析式为y=x +3. ················································· 3分 （2）n=4 ······················································································· 5分24.（1）证明：连接OC .∵OB=OC ， ∴∠B =∠OCB. ∵∠E =∠B ，∴∠E =∠OCB . ·······························································1分 ∵OD ⊥BC ， ∴∠E +∠DCE =90°. ∴∠OCB ＋∠DCE ＝90°. ∴∠OCE ＝90°. 即OC ⊥CE.∴CE 是⊙O 的切线．···························································2分 （2）∵OD ⊥BC ，∴∠CDE ＝90°.在Rt △CDE 中，DE =6 , CE=∴CD3.= …………………………..........................……… 3分 ∵OE ⊥BC ， ∴BC =2CD =6.∴DE=BC . ………………………………………………………………4分 ∵AB 是直径, ∴∠ACB ＝90°. ∴∠CDE=∠ACB. 在△ABC 与△CED 中，B E,BC DE ACB CDE.∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABC ≌△CED. ……………………………………….………5分 ∴AC=CD=3.∵O 是AB 的中点，D 是BC 的中点，∴1322OD AC ==. ···································································· 6分25.解：（1）由题意，A 点坐标为(0,1.25),B 点坐标为(2.5,0). …………………………1分设抛物线的解析式为y =a (x -1)2+k (a ≠0) …………….………………….… 2分 ∵抛物线经过点A ,点B .∴ ()21250251.a k,a .k.=+⎧⎪⎨=−+⎪⎩解得：1225a ,k ..=−⎧⎨=⎩∴y =-(x -1)2+2.25（0≤x ≤2.5）. ……………………………….…………… 3分 ∴x =1时，y =2.25.∴水流喷出的最大高度为2.25 m. ………………………………..……… 4分（2）2.7 ························································································ 6分 26. 解：（1）∵点（2，m ）在20y ax bx c(a )=++>上，∴m ＝4a ＋2b ＋c .又∵m ＝c ，∴4a ＋2b ＝0.∴b ＝-2a . ∴2122b a t a a−=−=−=. …………..………………………………………2分 （2）∵点（2，m ）在抛物线2(0)y ax bx c a 上， ∴m =4a +2b +c.∵c < m ,∴m - c>0.∴m -c =4a +2b >0.∴2a +b >0. ············································································ 3分 ∵点(-1,y 1),(3,y 2)在抛物线2(0)yax bx c a 上,∴y 1=a -b+c ，y 2=9a+3b+c,∴y 2-y 1=(9a+3b+c )-( a -b+c )=8a +4b =4(2a+b ). ································ 4分 ∵2a +b >0,∴4(2a +b )>0,∴y 2-y 1>0.∴y 2>y 1. ………………………………………………………………….6分27. （1）解：补全图形如图所示； (1)分（2）证明：∵∠BAC =90°， ∴∠ACP +∠APC =90°．∵以P 为中心，将线段PC 顺时针旋转90°得到线段PD ，∴∠DPC =90°.∴∠APC +∠BPD =90°．∴∠ACP =∠DPB ． ···························································· 3分 （3）线段BC ，BP ，BD =BD +BC. ………………4分证明：过点P 作PE ⊥PB 交BC 的延长线于点E .∵PE ⊥PB ，∴∠BPE =90°.∵∠DPC =90°，∴∠1+∠BPC =∠2+∠BPC =90°.∴∠1=∠2. ······································································· 5分 ∵AB =AC ，∠BAC =90°，∴∠ABC =∠ACB =45°.∵∠BPE =90°，∴∠PBE =∠PEB =45°.∴PB =PE . ········································································ 6分 在△PBD 与△PEC 中，12.PB PE PD PC =⎧⎪∠=∠⎨⎪=⎩，， ∴△PBD ≌△PEC .∴BD =EC .∵BE ==.BP =BD +BC ．····························································· 7分28. 解：（1）① A ，C ； ········································································ 2分②()21,，)21,+； ······················································ 5分 （2）-11 ≤ t ≤ 3. ············································································ 7分。

1.已知全集U={1,2,3,4,5,6},集合M={1,3,5},N={2,3,4},则M∩N=()A.{2,3,4}B.{1,3,5}C.{3}D.{2,3}答案：C.{3}评分标准：正确答案得1分，错误答案得0分。

2.已知三个数a，b，c，满足a＞b＞c，以及a＋b＋c＝20，则a＞()A.10B.8C.6D.5答案：A.10评分标准：正确答案得1分，错误答案得0分。

3.在△ABC中，若∠A＝90°，B＝(4,3)，C＝(6,1)，则∠ABC的面积()A.3B.9C.6D.12答案：B.9评分标准：正确答案得1分，错误答案得0分。

4.设x为实数，则“x＞1”是“x＋2＞3”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案：B.必要不充分条件评分标准：正确答案得1分，错误答案得0分。

5.已知f(x)=x＋2，若f(x)＋f(y)=7，则x＋y的值为()A.5B.9C.10D.11答案：A.5评分标准：正确答案得1分，错误答案得0分。

6.若a＞0，且2a＋3b＝8,则a＋b的最大值为()A.4B.5C.6D.8答案：B.5评分标准：正确答案得1分，错误答案得0分。

7.已知a＝5sin2x，b＝5cos2x，则a＋b的取值范围为( )A.[-2,2]B.[-5,5]C.[0,5]D.[0,10]答案：B.[-5,5]评分标准：正确答案得1分，错误答案得0分。

通州区2023-2024学年第一学期九年级期末质量检测数学试卷参考答案及评分标准2024年1月一、 选择题（本题共8个小题，每小题2分，共16分）二、 填空题（本题共8个小题，每小题2分，共16分） 9. 23π 10. 1211. 4 12. 2 13. R ≥1 14. 50° 15. 6 16. （1）4545， （2）90三、解答题（本题共68分，第17-22题每题5分；第23-26题每题6分；第27-28题每题7分）解答应写出文字说明、演算步骤或证明过程．17. 解：原式=2121422⎛⎫⨯−+⨯ ⎪ ⎪⎝⎭…………………3分 =52…………………5分 18. 解：在Rt △ABC 中，BC ＝6，tan A ＝34 ∴AC=8 …………………2分∴AB=10 …………………3分∴cos B = 35BC AB = …………………5分 19. 解：（1）∵二次函数图象经过点（-1，0）和（3，0）∴该二次函数图象的对称轴为直线x ＝1 …………………2分（2）由题意可知：二次函数图象的顶点坐标为（1，-4） …………………3分∴设该二次函数表达式为：()()2140y a x a =−−≠将（3，0）点代入得：440a −=∴1a = …………………4分∴223y x x =−−…………………5分20. 解：在Rt △ADC 中，CD =2，AC=，∴tan ∠CAD＝3CD CA == …………………1分 ∴∠CAD ＝30° …………………2分∵AD 平分∠CAB∴∠CAB ＝2∠CAD =60° …………………3分在Rt △ABC 中，∠B =30°∴AB =2AC= …………………5分21. 解：过点A 作AD ⊥BC 于点D …………………1分∴∠B ＝45°，∠C ＝30°在Rt △ABD 中，AD =BD=200 …………………2分在Rt △ACD 中，CD…………………3分∴CB =200+ …………………4分答：小山两端B ，C之间的距离为(200+米. ………5分22. （1）…………………3分（2）证明：连接AD ，∵点A ，B ，C ，D 在⊙O 上，AD ＝BC ，∴ AD ＝BC ． …………………4分∴ ∠DBA ＝∠CAB （ 等弧所对的圆周角相等）（填推理的依据）．…………………5分 ∴ BD ∥AC ．23. （1）证明：连结CD …………………1分∵BC 为半圆的直径∴∠BDC ＝90° …………………2分D∴BD ⊥CD∵CA CB =∴点D 为AB 的中点 .………………3分（2）方法一：证明：∵CA CB = ∴∠B ＝∠A∵四边形BCED 为圆内接四边形∴∠AED ＝∠B …………………………………4分∴∠AED ＝∠A …………………………………5分∴AD DE =. …………………………………6分方法二：证明：连结DO ，EO ，∵CA CB =，AD=BD ，∴∠ACD =∠BCD ……………………4分 ∵ 2DOE ACD ∠=∠，2DOB BCD ∠=∠，∴ ∠DOE =∠DOB ．∴∴ BD=DE ．……………………5分 ∵ AD=BD ，∴AD DE =．……………………6分24. 解：（1）∵直线2y kx =+与双曲线6y x =的一个交点是(,3)A m ∴把点(,3)A m 代入6y x=中，得36m =，2m = ……………………1分 ∴把点(2,3)A 代入2y kx =+，得223k +=，12k =. ……………………2分 （2）点(6,1)P 或(6,1)−−. ……………………6分25.（1）证明：连结OD∵AB 为⊙O 的直径∴∠ACB=90°∵CD 平分∠ACBEDC O A ED A F D O∴∠ACD=45° ……………………1分∴∠AOD=2∠ACD =90° ……………………2分∵DF ∥AB∴∠AOD+∠ODF =180°∴∠ODF =90°∴直线DF 是⊙O 的切线. ……………………3分（2）解：在Rt △ABC 中，∠A ＝30°，AC =∴4BC =，8AB = ……………………4分∴4OD =∵∠COB =60°又∵DF ∥AB∴∠F =60° ……………………5分在Rt △ODF 中，3==. ……………………6分26. 解：（1）∵()222211y x mx m x m =−+−=−− …………………………1分 ∴抛物线顶点坐标为（m ，-1）． …………………………2分（2）y 1 < y 2． …………………………3分（3）∵抛物线对称轴为直线x ＝m ，∴点（4，y 2）关于对称轴的对称点为（2m -4，y 2），…………………………4分 ∵抛物线开口向上，y 1≤y 2，∴2m -4≤x 1＜4，∴2m -4≤-1，解得m ≤32．………………………………………………………………………6分 27. （1）如图 …………………………1分 （2）BE = 2CF ，BE ⊥CF 证明：取AC 中点M ，连结FM ∵F 为AD 中点 ∴FM ∥CD ，12FM CD =数学试卷答案第5页（共5页）∵线段CD 绕点C 顺时针旋转90°得到线段CE ∴12FM CE = ∵AC = BC ∴1122CM AC CB == ∴CM FMBC EC=…………………………2分 ∵FM ∥CD∴∠FMC +∠DCA =180°∴∠FMC =180°-∠DCA =90°-∠ECA ∵∠BCE =90°-∠ECA∴∠FMC =∠BCE …………………………3分∴△FMC ∽△ECB …………………………4分 ∴BE = 2CF ，∠BEC =∠CFM …………………………5分 ∵DC ⊥CE ∴FM ⊥CE∴∠FCE +∠CFM =90°∴∠FCE +∠BEC =90° …………………………6分 ∴BE ⊥CF . …………………………7分 注：方法不唯一，酌情给分 28. 解：（1）P 1N 1，P 2N 2.（2）由题意，可得PN ＝2MN . ∵MN ≤2，∴PN ≤4.如图，当OP =3且点P 在直线x ＝2上时， ∵OH ＝2，∴'PH P H ==结合图形，点P 的纵坐标取值范围为P y （3）11≤≤b −．…………………………………2分…………………………………5分 …………………………………7分。