2014检测答案
- 格式:doc
- 大小:57.50 KB
- 文档页数:5

黄冈市2014年高三年级4月份质量检测考试(文科综合)历史试题参考答案24.【答案】D 【解析】结合材料和所学知识对比分析秦汉与隋唐宋,不难发现两个时期各自的政治结构、经济格局和选官制度都有“变化”。
政治方面,三公九卿制向三省六部制转变(或贵族制度向官僚制度转变)察举制向科举制转变;经济格局方面,经济重心由北方转移到南方。
A、B、C三项都仅是变化的一个方面,只有D项符合题意。
25.【答案】D 【解析】材料着重强调政府财政分配以商品贸易的方式进行,说明宋代商品经济高度发达,故D项正确。
材料中只说明政府垄断货币发行,并未说明是金属货币还是纸币,A项错误。
材料中并未涉及征收赋税方式的变化,故B项不正确。
C项在材料中未能体现。
26.【答案】A 【解析】本题解题关键是审题目选项,A项的说法直接体现了材料意思也反映了改土归流的实质目的;B项主要目的不是稳定地方;C、D两项都是改土归流的出发点之一,但不是最主要的目的。
故符合题意的正确答案为A项。
27.【答案】D 【解析】解答本题的关键在于掌握亚里士多德生活时代的政治制度的特征及其话语的含义。
当时雅典实行的直接民主,不是精英政治(代议制),故A不符合题意。
B、C项是代议制民主情形下社会状况,故B、C理解错误。
D项符合直接民主情形下人们的追求。
28.【答案】C 【解析】本段材料的主旨强调英国人是议会的奴隶,议会选出后国人无话语权了,即议会专权,这是批评英国的议会制;同时,为了防止代议制下的议会专权,卢梭主张法律应该由全体公民集会讨论并通过,这表明他反对代议制,即反对精英政治,推崇直接民主。
29.【答案】C 【解析】材料中的“候选人”和“主流思想”,说明美国总统候选人要想获得选举成功,就要符合主流民众的利益,这是美国总统制共和制的必然结果,故选C项。
A、B两项不能完全体现美国政治的特点和其本质,C项与题意不符。
30.【答案】D 【解析】解答本题的关键在于理解材料的主旨。

珠海市2013-2014 学年度第二学期高三学生学业质量监测语文参考答案及评分标准1.C【解析】C.tì/tíqǐng/qīng jiã/jiē;A.gěng kān/shân dāng/dàng;B.tāhē/kējuã/jiáo;D.chǔ/zhùbâi/p ãi jiě2.A【解析】过犹不及——过:过分;犹:像;不及:达不到。
事情做得过头,就跟做得不够一样,都是不合适的。
应用“更胜一筹”,更胜一筹:指技艺或技术超过别人一些。
筹:指程度。
胜:指超过。
B 项“恰如其分”指办事或说话正合分寸。
C 项“泾渭分明”泾河水清,渭河水浑,泾河的水流入渭河时,清浊不混。
比喻界限清楚或是非分明。
D 项“厘定”书面语,整理规定3.C【解析】本题重点考查考生正确辨析病句的能力。
A.否定不当,欠缺与“不当”“不稳”构成双重否定,表示肯定,与实际相反,去掉“不当”“不稳”;B.搭配不当,“植被覆盖率”与“十分严重”不搭配。
D. 项是歧义,“全国几十个报社的编辑记者”可作两种理解:“全国/几十个报社/的编辑记者”“全国/几十个,/报社的编辑记者”4.D Ks5u【解析】本题重点考查考生语言表达连贯和文段逻辑顺序安排的能力。
作此题宜结合排除法,先通读语段,大致了解材料信息中心思想,再根据结构以及语意关系判断其先后顺序。
注意:抓住“汉字”的审美和文化内涵入手解题。
第④句与上文句式的一致。
5.B【解析】掩袭,偷袭。
6.B【解析】B.连词,表修饰;A.动词,去,到/代词,代指临颍城;C.介词,到/介词,在;D.介词,用/连词,表目的,来。
7. B【解析】本题第一处应在“曰”后断。
对话、引语是古文断句的一重要依据。
对话、引语常用“曰”“云”“言”“白”“语”“道”“谓”“对”等为标志。
“郾城危在旦夕”为一个主谓句,且“危在旦夕”为一个成语,后面需要停顿。

2014年大田县初中毕业班学业质量检测语文参考答案及评分说明一、积累与运用(22分)(一)古诗文积累(22分)1.(12分)(本题每空1分,错、漏、添字的,该空不给分)(1)(2分)不亦乐乎人不知而不愠(2)(2分)惟吾德馨草色入帘青(3)(2分)东临碣石水何澹澹(4)(2分)月有阴情圆缺此事古难全(5)(2分)衣食所安必以分人(6)(2分)风霜高洁水落而石出(二)(10分)2.(4分,各1分)①(筛)②(梁)③(A )④(B)3.(2分)(B)4.(4分, 各2分,言之成理即可)(1)示例:大田县慢慢形成了现今多种剧种并存的局面.....。
(2)示例一:农村戏台很简单,找一块空地,几根柱子、几根横liáng、几块木板就搭成。
示例二:农村戏台很简单,(在一块空地上,)找几根柱子、几根横liáng、几块木板就搭成。
二、综合性学习(10分)5.(4分,各2分)示例:6. ①食品安全存在严重的问题;②政府三个“最严”保“舌尖上的安全”。
③行政部门已经对黑心者实施监测打击。
(答出两点,言之成理即可)6.(2分)示例:安全食品连万家,食品安全靠大家;人人关心食品安全、家家享受健康生活;关注食品安全,构建和谐社会;群策群力共筑食品安全,同心同德共享健康生活;普及饮食安全知识,创造精彩健康生活。
(答出一条,能够扣住主题,符合广告语要求即可)7.(4分)示例一:刘明,你在买食品的时候,可要注意看食品标签,观察是否有注明生产厂家、出厂日期和保质期,否则,可能就是不安全食品了,就不要购买哦。
(大意对即可,点出标签三有(厂家、出厂日期和保质期)得2分,其它表述2分)三、阅读(58分)(一)(18分)8.(4分,各1分)(1)鞭打(2)等到(3)统领(4)逃亡9.(2分) B10.(4分)(1)吴广故意多次说要逃跑,使军官恼怒,让他们责辱他,(借此)来激怒士卒。
(2)我听说,做事情抢先一步就能控制别人,落后一步就要被人控制。
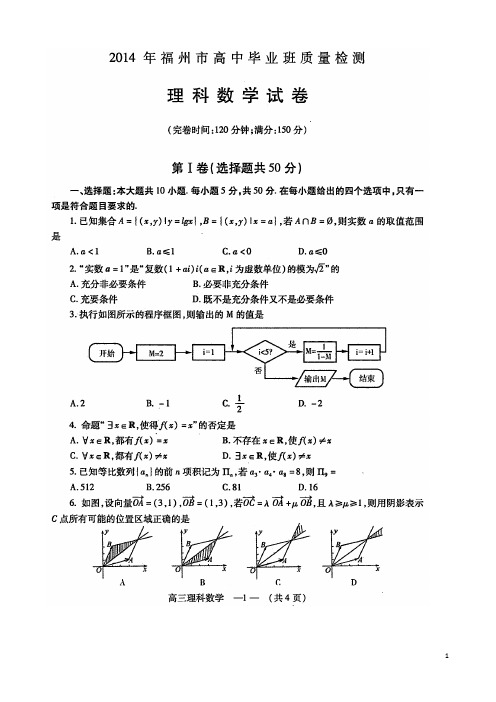
2014年福州市高中毕业班质量检测 数学(理科)试卷参考答案及评分标准1—10 DABCA DCBBD11.96 12.1/3 13.0 14.18+32 cm 2 15.804216. 解:(I)甲厂抽取的样本中优等品有7件,优等品率为7.10 乙厂抽取的样本中优等品有8件,优等品率为84.105=………………4分 (II)ξ的取值为1,2,3. ………………5分12823101(1),15C C P C ξ⋅===………………7分21823107(2),15C C P C ξ⋅===………………9分157)3(3100238=⋅==C C C P ξ………11分 所以ξ的分布列为17712123.1515155E ξξ=⨯+⨯+⨯=的数学期望为()……13分 17. 解:(I)2()2cos 2f x x x ==cos221x x +=2sin 216x π⎛⎫++ ⎪⎝⎭……………2分 令-222,262k x k k Z πππππ+≤+≤+∈,解得322322ππππ+≤≤-k x k 即63ππππ+≤≤-k x k …………4分 [0,]2x π∈,∴f (x )的递增区间为]6,0[π………………6分(Ⅱ)由21)62sin(2)(=++=πC C f ,得21)62sin(=+πC而()0,C π∈,所以132,666C πππ⎛⎫+∈ ⎪⎝⎭,所以5266C ππ+=得3C π=8⋅⋅⋅⋅⋅⋅⋅⋅⋅分 因为向量)sin ,1(A m =与向量)sin ,2(B n =共线,所以sin 1sin 2A B =,由正弦定理得:21=b a ①…10分由余弦定理得:3cos2222πab b a c -+=,即a 2+b 2-ab =9 ②………12分由①②解得32,3==b a ……………13分18. 解:(Ⅰ)证明:∵点E 、F 分别是AB 、CD 的中点,∴EF //BC 又∠ABC =90°∴AE ⊥EF ,∵平面AEFD ⊥平面EBCF ,∴AE ⊥平面EBCF ,AE ⊥EF ,AE ⊥BE , 又BE ⊥EF ,如图建立空间坐标系E ﹣xyz .……………2分翻折前,连结AC 交EF 于点G,此时点G 使得AG+GC 最小. EG =12BC =2,又∵EA=EB =2. 则A (0,0,2),B (2,0,0),C (2,4,0), D (0,2,2),E (0,0,0),G (0,2,0),∴=(﹣2,2,2),CG=(-2,-2,0) ∴BD CG ⋅=(﹣2,2,2)(-2,-2,0)=0, ∴BD ⊥CG ………………5分 (Ⅱ)设EG=k ,AD ∥平面EFCB ,∴点D 到平面EFCB 的距离为即为点A 到平面EFCB 的距离.S 四形GBCF =12[(3- k )+4]×2=7-k D GBCF V S AE 四形GBCF -\=鬃13=2(7)3k - 又B ADGE ADGE V S BE 四形-= 13=2(2)3k +,B ADGE D GBCF V V --=2,∴4(2)3k +=2(7)3k -,1k ∴=即EG =1…………………8分设平面DBG 的法向量为1(,,)n x y z =,∵G (0,1,0),∴(2,1,0),BG =- BD = (-2,2,2), 则 1100n BD n BG ⎧⋅=⎪⎨⋅=⎪⎩,即222020 x y z x y -++=⎧⎨-+=⎩取x =1,则y =2,z =-1,∴(1,2,1)n =-…………………10分面BCG 的一个法向量为2(0,0,1)n = 则cos<12,n n>=1212||||n n n n =…………………12分由于所求二面角D-BF-C 的平面角为锐角,所以此二面角平面角的余弦值为6……………………13分 19. 解: (Ⅰ)设动圆圆心M (x ,y ),依题意点M 的轨迹是以(1,0)为焦点,直线x =-1为准线的抛物线………2分 其方程为y 2=4x .- …………3分(Ⅱ)设A (x 1,y 1),B (x 2,y 2).由题意得x 1≠x 2(否则αβπ+=)且x 1x 2≠0,则4,4222211y x y x == 所以直线AB 的斜率存在,设直线AB 的方程为y=kx+b ,则将 y=kx+b 与y 2=4x 联立消去x ,得ky 2-4y +4b =0 由韦达定理得kby y k y y 4,42121==+-------※…………6分 ①当βα+=2π时,tan tan 1αβ⋅=所以121212121,0y yx x y y x x ⋅=-=,…………7分 所以y 1y 2=16,又由※知:y 1y 2=kb4所以b =4k ;因此直线AB 的方程可表示为y=kx+4k,所以直线AB 恒过定点(-4,0). …………8分 ②当αβ+为定值(0)θθπ<<时.若βα+=2π,由①知,直线AB 恒过定点M (-4,0) …………9分 当2πθ≠时,由αβθ+=,得tan tan()θαβ=+=tan tan 1tan tan αβαβ+-=16)(42121-+y y y y将※式代入上式整理化简可得:k b 44tan -=θ,所以θtan 44+=k b ,…………11分此时,直线AB 的方程可表示为y=kx +θtan 44+k ,所以直线AB 恒过定点)tan 4,4(θ-…………12分 所以当2πθ=时,直线AB 恒过定点(-4,0).,当2πθ≠时直线AB 恒过定点)tan 4,4(θ-.…………13分 20. 解:(I)f (x )的定义域为),1(+∞-a .其导数'()a x f x a ax x a=-=-++211………1分①当0a <时,'()0f x >,函数在),1(+∞-a上是增函数;…………2分 ②当0a >时,在区间(,)a-10上,'()0f x >;在区间(0,+∞)上,'()0f x <. 所以()f x 在(,)a-10是增函数,在(0,+∞)是减函数. …………4分 (II)当0a <时, 取1x e a =-,则11()1()2()011f e a e a ae e e a a a a-=--=->-=->, 不合题意.当0a >时令()()h x ax f x =-,则1()2ln()h x ax x a=-+………6分问题化为求()0h x >恒成立时a 的取值范围. 由于'12()12()211a x a h x a x x a a+=-=++ ………7分 ∴在区间(,)a a --112上,0)('<x h ;在区间),21(+∞-a 上,0)('>x h . ()h x ∴的最小值为1()2h a -,所以只需1()02h a->即1112()ln()022a a a a ⋅---+>,1ln 12a ∴<-,2e a ∴>………9分 (Ⅲ)由于当0a <时函数在),1(+∞-a上是增函数,不满足题意,所以0a >构造函数:()()()g x f x f x =--(10x a -<<)11()ln()ln()2g x x x ax a a∴=--++………11分则2'22112()20111ax g x a x x x a a a=-+=<-+-所以函数)(x g 在区间1(,0)a -上为减函数. 110x a-<<,则1()(0)0g x g >=, 于是()()f x f x -->110,又1()0f x =,()()f x f x ->=120,由()f x 在,)+∞(0上为减函数可知21x x >-.即120x x +>…………………14分 21. (1)(本小题满分7分)选修4-2:矩阵与变换解: (Ⅰ)法一:依题意,⎩⎨⎧==∴⎩⎨⎧-=-=+42,2236d c d c d c .⎪⎪⎭⎫ ⎝⎛=4233A . ………… 2分所以⎪⎪⎪⎪⎭⎫⎝⎛--=-213121321A …………4分 法二:033)3(0332=-++-=----c d d dcλλλλ即的两个根为6和1,故d =4,c =2. ⎪⎪⎭⎫⎝⎛=∴4233A …………2分所以⎪⎪⎪⎪⎭⎫ ⎝⎛--=-213121321A -…………4分 (Ⅱ)法一:⎪⎪⎭⎫⎝⎛-41=2⎪⎪⎭⎫ ⎝⎛11-⎪⎪⎭⎫⎝⎛-23…………5分 A 3⎪⎪⎭⎫⎝⎛-41=2×63⎪⎪⎭⎫ ⎝⎛11-13⎪⎪⎭⎫ ⎝⎛-23=⎪⎪⎭⎫ ⎝⎛434429…………7分 (2)(本小题满分7分)选修4-4:坐标系与参数方程.解:(Ⅰ)(曲线C 的直角坐标方程为y 2=4x , 直线l 的普通方程x -y -2=0. ………..4分(Ⅱ)直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+-=+-=t y tx 224222(t 为参数),代入y 2=4x , 得到0482122=+-t t ,设M ,N 对应的参数分别为t 1,t 2则048,2122121>==+t t t t 所以|PM |+|PN|=|t 1+t 2|=212…………7分 (3) )(本小题满分7分)选修4-5:不等式选讲解:(Ⅰ)f (x )=|x -4|+|x -3|≥|(x -4)-(x -3)|=1,故函数f (x )的最小值为1. m =1. …………4分 (Ⅱ)由柯西不等式(a 2+b 2+c 2)(12+22+32)≥(a +2b +3c )2=1----------5分 故a 2+b 2+c 2≥141-…………6分 当且仅当143,71,141===c b a 时取等号…………7分。

医学检验专业知识真题2014年(3)一、单项选择题(下列各项备选答案中只有一项符合题意)1. 标本溶血不会影响下列哪项检验?______A.红细胞计数B.血细胞比容测定C.白细胞计数D.血清钾测定答案:C2. 有关中性粒细胞胞质内毒性颗粒的叙述,错误的是______。
A.染色呈黑色或者黑紫色B.可覆盖于中性粒细胞核上C.比正常中性颗粒粗大D.易与嗜碱性粒细胞混淆答案:B[解答] 中毒颗粒比正常中性颗粒粗大,大小不等,分布不均匀,染色较深,呈黑色或紫黑色。
有时颗粒很粗大,与嗜碱粒细胞易混淆;有时又小而稀少,散杂在正常中性颗粒之中。
3. 有关网织红细胞的叙述,错误的是______。
A.网织红细胞比成熟红细胞体积大B.ICSH将网织红细胞分为四型C.计数网织红细胞用新亚甲蓝染色D.网织红细胞内网织结构越多,细胞越成熟答案:D[解答] 红细胞在骨髓中生成,至发育为成熟红细胞,经历了不同阶段:干细胞、原始红细胞、早幼红细胞、中幼红细胞、晚幼红细胞、网织红细胞,最后发育为成熟红细胞。
随着细胞的成熟,RNA含量逐渐减低,至细胞完全成熟后消失或接近消失,即红细胞中网线状结构越多,表示细胞越幼稚。
4. 尿液中小圆上皮细胞是指______。
A.中层移行上皮细胞B.底层移行上皮细胞C.底层移行上皮细胞和肾小管上皮细胞D.肾小管上皮细胞答案:C[解答] 尿沉渣中小圆上皮细胞包括肾小管上皮细胞和基底层移行上皮细胞,其数量增加,临床常认为提示有肾小管损害或存在泌尿系统感染。
5. WHO将精子活动力分为几级______。
A.2级B.3级C.4级D.5级答案:C[解答] 精子的活动力直接反映精子的质量,WHO推荐的方法,把精子活动力分为:①0级表示不活动,无前向活动;②1级表示活动不良,前向运动微弱;③2级表示活动一般,有中等前向运动;④3级表示活动良好,前向运动活跃。
6. 不会引起白细胞增多的疾病是______。
A.急性链球菌感染B.急性失血C.急性溶血D.病毒性感染答案:C[解答] 造成白细胞升高的原因有生理性白细胞增高和病理性白细胞增高。

2014年高二下学期数学质量检测一、选择题:本大题共10小题,每小题5分,共50分. 1.已知i 是虚数单位,复数ii i z -+++-=12221,则=z ( C )A.1B. 2C.5 D. 222.某人进行了如下的“三段论”推理:如果f ′(x 0)=0,则x=x 0是函数f (x )的极值点中,因为函数f (x )=x 3在x=0处的导数值f ′(0)=0,所以x=0是函数f (x )=x 3的极值点.你认为以上推理的( B )A. 小前提错误B. 大前提错误C. 推理形式错误D. 结论正确3.不等式|x+3|﹣|2x ﹣2|≤a 2﹣3a 对任意实数x 恒成立,则实数a 的取值范围为( A ) A.(﹣∞,﹣1]∪[4,+∞) B.(﹣∞,﹣2]∪[5,+∞) C. [1,2] D.(﹣∞,1]∪[2,+∞) 4.设0,b a >> 则222b ab a +-的最小值为 ( C )A. 2B. 3C. 6D.无最小值5.已知函数f (x )=lg,若f (a )+f (b )=0且0<a <b <1,则ab 的取值范围是( D )A .(0,]B .(0,)C .(0,]D .(0,) 6.已知,22,223,a b a b a b a b ≤+≤≤-≤+满足-1则的范围是( A ) A 、[1955-,] B 、[1855-,] C 、[905,] D [805,]7.如图,在由x =0,y =0,x =及y =cosx 围成区域内任取一点,则该点落在x =0,y =sinx 及y =cosx围成的区域内(阴影部分)的概率为( B )A 、1-2B 1C 、12D 、3-8.设函数f (x )=(x -1)k cosx (k *N ∈),则( C ) A 、当k =2013时,f (x )在x =1处取得极小值 B 、当k =2013时,f (x )在x =1处取得极大值 C 、当k =2014时,f (x )在x =1处取得极小值 D 、当k =2014时,f (x )在x =1处取得极大值9.设正实数x ,y ,z 满足x 2﹣3xy+4y 2﹣z=0.则当取得最大值时,的最大值为(B )10.对于一个有限数列()12n P P P P =,,,,P 的蔡查罗和(蔡查罗为一数学家)定义为()121n S S S n+++,其中()121k k S P P P k n =+++≤≤,若一个99项的数列()1299P P P ,,,的蔡查罗和为1000,那么100项数列()12991P P P ,,,,的蔡查罗和为( A ) A .991 B.992 C.993 D.999二、填空题:本大题共5小题,每小题5分,共25分. 11. 不等式12(log (2)1)(sin 2)0x x ---<的解集是_5242x x x ⎧⎫<<>⎨⎬⎩⎭或_________12. 若21<<-a ,12<<-b ,则a -|b|的取值范围是 (-3,2) .13.如图,对正方形纸片ABCD 进行如下操作:第一步,过点D 任作一条直线与BC 边相交于点E 1,记∠CDE 1=α1;第二步,作∠ADE 1的平分线交AB 边于点E 2,记∠ADE 2=α2;第三步,作∠CDE 2的平分线交BC 边于点E 3,记∠CDE 3=α3;按此作法从第二步起重复以上步骤…,得到α1,α2,…,αn ,…,则用αn 和αn+1表示的递推关系式是αn+1= .14.不等关系有下列基本性质:①,a b b c a c >>⇒>;②a b a c b c >⇒+>+; ③0,0a b c d ac bd >>>>⇒>;④0nna b a b >>⇒>我们用记号“|”表示两个正整数间的整除关系,如3|12表示3整除12.试类比课本中不等关系的基本性质,写出整除关系的两个性质.①___________________________;②_________________________.15.已知函数1()()2ln()f x a x x a Rx=--∈函数()ag xx=-若至少存在一个x0∈[1,e],使得f(x o)>g(x o)成立, a的取值范围是a>0 .三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)已知z=1+i.(1)设ω=z2+3﹣4,求ω;(2)如果,求实数a,b的值.+3﹣,有=17.(本小题满分12分)已知函数f(x)=ax2+x﹣a(﹣1≤x≤1),且|a|≤1.求证:|f(x)|.证明:∵﹣1≤x≤1,∴|x|≤1,又∵|a|≤1,∴|f(x)|=|a(x2﹣1)+x|≤|a(x2﹣1)|+|x|≤|(x2﹣1)|+|x|=1﹣|x|2+|x|=﹣(|x|﹣)2+≤.所以:|f(x)|.18.(本小题满分12分)某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).(1)求θ关于x的函数关系式;(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为y,求y关于x的函数关系式,并求出x为何值时,y 取得最大值?解:(1)由题意,30=xθ+10θ+2(10﹣x),∴θ=(0<x<10);(2)花坛的面积为﹣==(10﹣x)(5+x);装饰总费用为xθ•9+10θ•9+2(10﹣x)•4=9xθ+90θ+8(10﹣x)=170+10x,∴花坛的面积与装饰总费用的比为y=.令17+x=t,则y=,当且仅当t=18时取等号,此时x=1,θ=,∴出x=1时,y取得最大值.19.(本小题满分12分)设函数f(x)=|x﹣3|﹣|x+1|,x∈R.(Ⅰ)解不等式f(x)<﹣1;(Ⅱ)设函数g(x)=|x+a|﹣4,且g(x)≤f(x)在x∈[﹣2,2]上恒成立,求实数a的取值范围.解:(Ⅰ)∵函数f(x)=|x﹣3|﹣|x+1|=,故由不等式f(x)<﹣1可得x>3 或.解得x>.(Ⅱ)∵函数g(x)=|x+a|﹣4,且g(x)≤f(x)在x∈[﹣2,2]上恒成立,∴|x+a|﹣4≤|x﹣3|﹣|x+1|在x∈[﹣2,2]上恒成立,在同一个坐标系中画出函数y=f(x)和y=g(x)的图象,如图所示:故当x∈[﹣2,2]时,若0≤﹣a≤4时,则函数g(x)在函数f(x)的图象的下方,g(x)≤f(x)在x∈[﹣2,2]上恒成立,求得﹣4≤a≤0,故所求的实数a的取值范围为[﹣4,0].20.(本小题满分13分)已知函数()ln (0)f x x p >.(Ⅰ)若函数()f x 在定义域内为增函数,求实数p 的取值范围; (Ⅱ)当*∈N n时,试判断1nk =与2ln(1)n +的大小关系,并证明你的结论; 解:(Ⅰ)0p >,函数()ln f x x =的定义域为[1,)+∞.1()f x x'=-.1x ≥在(1,)x ∈+∞恒成立,24(1)x p x -∴≥在(1,)x ∈+∞恒成立. 224(1)1114[()]124x x x -=--+≤, 1p ∴≥,∴p 的取值范围为[1,)+∞. ……………………………………………………… (6分) (Ⅱ)当*n N ∈时,1nk=2ln(1)n >+. 证明:当*n N ∈时,欲证1nk =2ln(1)n >+*2[ln(1)ln ]()k k k N >+-∈. 由(Ⅰ)可知:取1p =,则()(1)(1)f x f x ≥≥,而()01=f ,ln x ≥(当1x =时,等号成立). 用21()x x +代换x 21ln()(0)x x x+>>,即2[ln(1)ln ](0)x x x x >+->, ∴*2[ln(1)ln ]()k k k N k>+-∈. 在上式中分别取1,2,3,,k n =,并将同向不等式相加,得1nk k=>∑2ln(1)n +. ∴当*n N ∈时,1nk k=∑2ln(1)n >+. …………………………………………21、(本小题满分14分)下面四个图案,都是由小正三角形构成,设第n个图形中所有小正三角形边上黑点的总数为f(n).(1)求出f(2),f(3),f(4),f(5);(2)找出f(n)与f(n+1)的关系,并求出f(n)的表达式;(3)求证:(n∈N*).解:(1)由题意有f(1)=3,f(2)=f(1)+3+3×2=12,f(3)=f(2)+3+3×4=27,f(4)=f(3)+3+3×6=48,f(5)=f(4)+3+3×8=75.…(2分)(2)由题意及(1)知,f(n+1)=f(n)+3+3×2n=f(n)+6n+3,…(4分)即f(n+1)﹣f(n)=6n+3,所以f(2)﹣f(1)=6×1+3,f(3)﹣f(2)=6×2+3,f(4)﹣f(3)=6×3+3,…f(n)﹣f(n﹣1)=6(n﹣1)+3,…(5分)将上面(n﹣1)个式子相加,得:f(n)﹣f(1)=6[1+2+3+…+(n﹣1)]+3(n﹣1)==3n2﹣3…(6分)又f(1)=3,所以f(n)=3n2.…(7分)(3)∵f(n)=3n2∴.…(9分)当n=1时,,原不等式成立.…(10分)当n=2时,,原不等式成立.…(11分)当n≥3时,==,原不等式成立.…(13分)综上所述,对于任意n∈N*,原不等式成立.…(14分)。
2014年初三毕业班质量检测数 学 试 题(满分: 150分;考试时间:120分钟)考生注意:本学科考试有两张试卷,分别是本试题(共4页26题)和答题卡.试题答案要填在答题卡相应的答题栏内,否则不能得分.一、选择题(本大题有7小题,每小题3分,共21分.每小题有四个选项,其中有且只有一个选项正确) 1.-3的相反数是(***) A .13-B. 13C. 3D. 3- 2.下列图形中既是..轴对称图形又是..中心对称图形的是(***)3.计算82⨯结果为(***)A .2B .4C .8D .164.已知2x =是一元二次方程220x mx ++=的一个解,则m 的值是(***)A .3-B .3C .2-D .2-或35.已知⊙1O 的半径r 为3cm ,⊙2O 的半径R 为4cm ,两圆的圆心距1O 2O 为1cm ,则这两圆的位置关系是(***)A .相交B .内含C .内切D .外切6.当实数x 的取值使得1-x 有意义时,函数3y x =-+中y 的取值范围是(***) A .2y < B .2y ≥ C .2y > D .2y ≤ 7.A .B .C .D .第15题``根据以上统计图,下列判断中错误的是(***) A.选Ⅰ的人有8人 B.选Ⅱ的人有4人 C. 选Ⅲ的人有26人 D.该班共有50人参加考试 二、填空题(本大题有10小题,每小题4分,共40分)8.在中国上海世博会园区中,中国馆的总占地面积为65 200m 2,这一数据用科学记数法表示为 *** m 2.9.不等式组的正整数解是 *** .10.如图,点A B C 、、在⊙O 上,若24BAC ∠=,则BOC ∠ = *** °.11.反比例函数的图象经过点(-1,2),则a 的值为 *** .12.已知等腰三角形的两条边长分别为2和5,则它的周长为 *** . 13.宁宁同学设计了一个计算程序,如下表根据表格中的数据的对应关系,可猜测a 的值是 *** .14.如图,在ABC ∆中,点D E 、分别在边AC AB 、上,DE ∥BC ,BC =6,DE =2,当ADE ∆面积是3时,则梯形DBCE 的面积是 *** . 15.如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若ABC ∆与111A B C ∆是位似图形,且顶点都在格点上,则位似中心的坐标是 *** .16.某班数学兴趣小组收集了本市4月份30天的日最高气温的数据,经过统计分析获得了两条信息和一个统计表如下: 信息Ⅰ:日最高气温的中位数是15.5C ;信息Ⅱ:日最高气温是17C 的天数比日最高气温是18C 的天数多4天.4月份日最高气温统计表OAB C第10题·a y x=237,31x x +>⎧⎨->-⎩1请根据上述信息回答4月份日最高气温的众数是 *** C .17.初三年级某班有54名学生,所在教室有6行9列座位,用(,)m n 表示第m 行第n 列的座位,新学期准备调整座位,设某个学生原来的座位为(,)m n ,如果调整后的座位为(,)i j ,则称该生作了平移[][],,a b m i n j =--,并称a b +为该生的位置数.若某生的位置数为8,则当m n +取最小值时,m n 的最大值为 *** .三、解答题(本大题有9小题,共89分) 18.(本题满分18分)(1)计算: 011)|3|(sin30)-+--.(2)已知:AOB ∠求作:P ∠,使得P ∠=AOB ∠(尺规作图,不写作法,保留作图痕迹).(3)先化简,再求值:24242a a a --+,其中2a =.19.(本题满分7分)如图,在ABC ∆中,AB AC =, CD ⊥AB , 垂足为D ,且 25BCD ∠=.求∠A 的大小.20.(本题满分8分) 欢欢有红色、白色、黄色三件上衣,又有米色、白色的两条裤子. (1)她随机拿出一件上衣和一条裤子,用树状图(或列表法)表示所有可能出现的结果;(2)如果欢欢最喜欢的穿着搭配是白色上衣配米色裤子,求欢欢随机拿出一件上衣和一条裤子正好是她最喜欢的穿着搭配的概率.21.(本题满分8分)如图,在平行四边形ABCF 中,︒=∠90BAC ,延长CF 到E ,使CE BC =,过E 作BC 的垂线,交BC 延长线于点D . 求证:AB CD =.22.( 本题满分8分) 若一次函数11y a x b =+(1110,a a b ≠、是常数)与22y a x b =+(2220,a a b ≠、是常数),满足12+0a a =且12+0b b =,则称这两函数是对称函数. (1)当函数3y mx =-与2y x n =+是对称函数,求m 和n 的值;(2)在平面直角坐标系中,一次函数23y x =+图象与x 轴交于点A 、与y 轴交于点B ,点C 与点B 关于x 轴对称,过点A 、C 的直线解析式是y kx b =+,求证:函数23y x =+与y kx b =+是对称函数.23.(本题满分9分)如图,ABC △中,24AB BC AC ===,,E F ,分别在AB AC ,上,沿EF 对折,使点A 落在BC 上的点D 处,且FD BC ⊥. (1)求ABC ∠的度数;(2)判断四边形AEDF 的形状,并证明你的结论.EABCDF第21题24.(本题满分9分)我省某工艺厂为全运会设计了一款工艺品的成本是20元∕件.投放市场进行试销后发现每天的销售量y (件)是售价x (元∕件)的一次函数,当售价为22元∕件时,每天销售量为380件;当售价为25元∕件时,每天的销售量为350件. (1)求y 与x 的函数关系式;(2)该工艺品售价定为每件多少元时,每天获得的利润最大?最大利润是多少元?(利润=销售收入-成本)25.(本题满分11分)如图,在ABC ∆中,AB AC =,以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ,点F 在AC 的延长线上,且12CBF CAB ∠=∠. (1)求证:直线BF 是⊙O 的切线; (2)若5AB =,sin CBF ∠=,求BC 的长.26.(本题满分11分)已知二次函数2248y x mx m =-+-. (1)当2x ≤时,函数值y 随x 的增大而减小,求m 的取值范围;(2)以抛物线2248y x mx m =-+-的顶点A 为一个顶点作该抛物线的内接正AMN ∆(M ,N 两点在抛物线上),请问:△AMN 的面积是与m 无关的定值吗?若是,请求出这个定值;若不是,请说明理由;(3)若抛物线2248y x mx m =-+-与x 轴交点的横坐标均为整数,求整数m 的值.FAB第25题答案及评分标准一、选择题(本大题有7小题,每小题3分,共21分) 1.C 2.B 3.B 4.A 5.C 6.D 7.C 二、填空题(本大题有10小题,每小题4分,共40分)8. 46.5210⨯ 9. 3 10. 48 11. -2 12. 12 13. 101114. 24 15. (9,0) 16. 17 17. 25 三、解答题本大题有9小题,共89分) 18. (本题满分18分) (1)解:011)|3|(sin30)-+--1113()2-=+- ……………………………… 4分132=+- …………………………………… 5分 2.= …………………………………… 6分(2)解: 画一边1分,画两弧各1分,画两弧相交1分,画另一边1分,结论1分,总共6分. (3)解:2424242(2)(2)242(2)424(2)(2)(2)(2)2(2)2(2)(2)2a a a a a a a a a a a a a a a a a a a -=--+-++---+==-+-++==-+- …………………………………… 3分当2a =时,原== . ……… 6分19. (本题满分7分)解:∵CD ⊥AB ,∴90BCD B ∠+∠= ………………… 1分∵25BCD ∠=,∴65B ∠=, …………… 2分∵在ABC ∆中,180A B ACB ∠+∠+∠=, ……… 3分AB AC =,B ACB ∠=∠ , …………………… 5分∴∠A =1802B -∠=50. …………………………… 7分 20. (本题满分8分)…………………………………… 1分 …………………………………… 4分解:(1)列表法:或树状图:上衣 红色 白色 黄色裤子 米色 白色 米色 白色 米色 白色……… 5分 (2)因为总共有6种选择,所以选中自己最喜欢的穿着搭配的概率为16. 或p (白,米)=61…………………………………… 8分 21. (本题满分8分)证明:在□ABCD 中,AB ∥CF, ………………… 1分∴∠2=∠B, ……………………………… 2分 ∵∠BAC=90º,ED ⊥BD,∴∠1=∠D=90º, …………………………………… 4分 ∵CE=BC, …………………………………… 5分 ∴△ABC ≌△DCE, …………………………………… 7分 ∴AB CD =. …………………………………… 8分22. (本题满分8分)解:(1)由题意可知2030m n +=⎧⎨-+=⎩,解得2,3.m n =-⎧⎨=⎩…………………………………… 2分 (2)A (23-,0),B (0,3), …………………………………… 3分 ∵点C 与点B 关于x 轴对称,∴B (0,-3), …………………………………… 5分第21题由题意可得30,23,k b b ⎧-+=⎪⎨⎪=-⎩ …………………………………… 6分解得2,3,k b =-⎧⎨=-⎩ 故y=-2x-3, …………………………………… 7分∵2+(-2)=0,3+(-3)=0,∴函数y=2x+3与y=kx+b 是对称函数. …………………………………… 8分 23. (本题满分9分)解:(1)在⊿ABC 中,AB=2,BC=32,AC=4,∵AB 2+BC 2=16 AC 2=16 …………………………………… 1分∴AB 2+BC 2=AC2…………………………………… 2分∴∠ABC=90o………………………………… 3分 (2)(方法一)AEDF 为菱形 …………………………………… 4分 设EF 与AD 相交于O ,由题意可得,EF 是AD 是垂直平分线,………… 5分∴AE=ED ,AF=FD ,……………………………… 6分 ∵FD ⊥B C ,∠ABC=90o ,∴FD ∥AB ,∴∠AEF=∠EFD ,…………………………………… 7分 ∵∠AOE=∠FOD ,AO=OD , ∴⊿AEO ≌⊿DFO ,∴AE=DF=AF=ED , …………………………………… 8分 ∴AEDF 为菱形. …………………………………… 9分 (方法二)FD BC ⊥,90ABC ∠=︒,∴//FD AB ,∴21∠=∠ …………………………………… 5分 又由题意可知2A ∠=∠, ∴1A ∠=∠,∴AF//ED∴四边形AEDF 为平行四边形. …………………………………… 7分由题意可知AE=ED …………………………………… 8分∴四边形AEDF 为菱形. …………………………………… 9分 24. (本题满分9分)解:(1)设y 与x 的函数关系式为 (0)y kx b k =+≠,…………………………………… 1分12 CDB EA。
2014年杭州市高一年级教学质量检测语文试题及参考答案及评分标准2014_6新高考新题目2014-06-25 21012014年杭州市高一年级教学质量检测语文试题及参考答案及评分标准考生须知1.本试卷分试题卷和答题卷,满分100分,考试时间l00分钟。
2.答题前,在答题卷密封区内填写学校、班级和姓名。
3.所有答案必须写在答题卷上,写在试题卷上无效。
4.考试结束,上交试题卷和答题卷。
一(18分)1.下列句子中没有错别字且加点字的注音正确的一项是(3分)A.面对突如奇来的冰雪灾情,电力、交通、公安等系统的干部职工恪(kè)尽职守,顽强拼搏,用自己的勇气、毅力和奉献精神,诠释着“责任”这沉甸甸的字眼。
B.我被这美丽的海的月夜慑服了,在丝绒般的天幕衬托下,海上那闪闪的明镜中娇美可爱的月姑娘的倩(qiàn)影在浪花中跳跃,仿佛在向大海展示它那婀娜的舞姿。
C.一名真正合格的狙(zū)击手,需要具备沉稳的心态、灵敏的反应和高超的射技,唯有如此,才能在紧急的事态中力挽狂澜,担当起制伏罪犯、解救人质的重大使命。
D.环保部门根据新修订的《中华人民共和国环境保护法》,依法对这家幅射有害核原料的企业实施按日计罚,使得两位企业领导面面相觑(qù),最终引咎辞职。
2.依次填入下列句子横线处的词语,最恰当的一项是(3分)①奥地利作家卡夫卡作品的深刻性,充分体现在他对人性有透切的了解,对世界中“人”的种种异化的存在状态有深切的关注。
②中唐时候由于社会动荡不安,民生也日趋凋敝,以诗歌的形式来反映民间疾苦的文人如张籍、元稹、自居易等一时并起。
③任何产品的质量都是和人民群众的切身利益的,生产经营企业和有关监督部门都要从思想上提高认识,从严把好质量关。
A.荒谬从而息息相关 B.荒谬因而休戚相关C.荒诞因而息息相关 D.荒诞从而休戚相关3.下列句子中,没有语病的一项是(3分)A.某市最近出台并实施“交通事故现场快速处置法”后,大大缓解了事故现场对道路通行的影响和拥堵的状况,收到了明显的成效。
2014学年第二学期五年级英语期中质量检测试卷答案听力部分(40%)一、 听录音,选出你所听到的选项,并把它的编号填在左边的括号里。
(本大题共10分,每小题1分) (A) 听录音,选择正确的图片。
1 .B 2. A.3. B. 4 B. 5. B.(B)听录音,选出你所听到的选项。
1 .A. 2. A. 3.A. 4 .A. 5. B.二.听录音,根据你所听到的问题,选出最佳应答,并把它的编号填在左边的括号里。
(本大题共10分,每小题2分)1 .A 2. C. 3. A. 4 . B. 5. B.二、 听录音,根据所给问题,选择正确答案,并把它的编号填在左边的括号里。
(本大题共10分,每小题2分)1 .A. 2. A. 3.A. 4 .A. 5. C三、 听录音,填上横线上所缺的单词,补全句子(本大题共10分,每小题2分)1. August2.breakfast3.walk4. September5.snowman笔试部分(60%)四、 判断下列每组单词中划线部分的读音是否相同,如相同,请写“√”,如不相同,请写“×”。
(本大题共5分,每小题1分) 1√2. √3. ×4. ×5. √.五、 选择填空。
(本大题共10分,每小题1分)1.B2.C3.C4.C5.A6.A7.B8.A9.C 10.C六、 根据括号里所给的中文提示,在横线上填上合适的单词,每空一词。
(本大题共7.5分,每小题1.5分)1. best2.April3. autumn/fall4. sportswear 5 swimming 七、 根据所给的标点符号,连词成句。
(本大题共10分,每小题2分) _1.Thanks for your email. 2. Children,do you like the pictures? 3. Why do you like spring? 4. There are beautiful flowers everywhere.5. When is the trip this year? 八、 根据图片提示,仿照例句写句子。
2.信号采样中为何使用采样保持器?采样是对连续变化的模拟信号定时测量,抽取样值.通过采样,一个在时间上连续变化的模拟信号就转换为随时间变化的脉冲信号。
为了便于量化和编码,需要将每次采样取得的样值暂存,保持不变,直到下一个采样脉冲的到来。
4.什么事智能传感器?什么是多传感器信息融合技术?智能传感器是传感器与计算机或微处理器赋予智能的结合,从而是兼有信息获取与信息处理双重功能的传感器系统。
利用不同时间与空间的多传感器信息资源,采用计算机技术对多传感器的观测信息在一定准则下加以自动分析、综合,以获得对被测对象的一致性解释与描述,并进行决策和估计的信息处理过程。
信息融合就是将多个信息源的信息进行综合处理,从而得出准确、深入和全面的结论。
6.请解释是么是模拟信号、离散信号、数字信号、物理可实现信号?模拟信号:模拟信号是指在某一自变量间隔内,信号的幅值可以取连续范围内的任意数值。
离散信号:离散信号是指自变量在某些不连续数值时才具有幅值的信号。
数字信号:作为离散信号特例,各离散点的幅值也作离散化,如以二进制的编码表示,则称之为数字信号。
能量信号:能量信号在所分析的区间(—∞;+∞),能量为有限值的信号称为能量信号,满足条件:2()x t dt ∞-∞<∞⎰ 矩形脉冲、减幅正弦波、衰减指数等信号均为能量信号。
物理可实现信号:物理可实现信号又称为单边信号,满足条件:t <0时,x(t)=0,即在时刻小于零时的一侧全为零,信号完全有时刻大于零的一侧确定。
在实际中出现的信号,大量的是物理可实现信号,因为这种信号反映了物理上的因果律。
8.自相关函数与互相关函数哪一个保留相位信息?哪一个为偶函数?自相关函数为偶函数,互相关函数保留相位信息。
10.什么是倒频谱?其有何应用价值?倒频变换(频-时变换)。
它是将自功率谱密度函数的对数值再做一次傅里叶变换。
变换的结果以τ为参数,τ的量纲为时间的量纲,与1/f 量纲相同,因此又称τ为倒频率。
运用倒频变换的结果得到倒频谱。
(1)倒谱变换与自相关函数相比较,其特点主要在于变换之前要对功率谱密度取对数。
(2)倒频谱是频谱的频谱,它能分析出复杂频谱图上的周期结构,分离和提取频谱中的周期成分。
(3)在功率谱密度图上,边频间距的分辨力受分析带宽的限制,分析带宽越宽,分辨力越差,甚至使某些边频信号不易分辨。
12. 请说明为何最大熵谱分析能够避免经典功率谱分析中常常存在的功率泄露。
MEM 谱没有数据家常带来的问题,起他是连续普,谱光滑,谱峰陡峭,频率分辨力强。
适用于段样本分析。
14. 设计出一个应用相关函数解决的问题,并说明如何解决?传声器和离它最近的墙壁的距离约等于该墙壁反射波所走过的全部路程。
计算过程是墙壁距离≈[路程差+扬声器和传声器的距离]÷2互相关函数的包络波峰之间的时序距离反映两种声波之间的路程时序差。
利用这个特点和声波在空气中的传播速度,可以计算反射物与传声器之间的距离。
这个距离=声速×路程时序/采样频率,声速=335m/s, 采样频率=48kHz 。
16. 结合公式说明短时傅里叶变换、小波变换较经典功率谱分析有何优点?短时傅里叶变换: 为了解决时频局部化的问题,可以给傅立叶变换加一个滑动的“时间窗”,这就是短时傅立叶变换,通常也称之为加窗傅立叶变换。
短时傅立叶变换的基本思想是把信号划分成许多小的时间间隔,用傅立叶变换分析每一个时间间隔,以便确定该时间间隔存在的频率。
可以起到时频双限作用。
小波变换:是强有力的时频分析(处理)工具,是在克服傅立叶变换缺点的基础上发展而来的。
它在时域和频域均具有很好的局部化特征,能够提供目标信号各个频率子段的频率信息。
被誉为“数学显微镜”。
11. 请说明噪声测量中为何采用分贝和倍频程的概念。
、分贝:正常人耳的听觉范围从Pa μ20至Pa 20,其绝对值相差数百万倍,因此,用它来评价声音的强弱很不方便。
为了减少评价指标的数量级,改用它的对数来表示,这就是常称的声压级。
一个声压级,等于这个声音的有效声压和基准声压比值的常用对数乘以20,单位为d B,这样人耳的听觉范围相当于声压级0-120dB ,这样就显著地减少了数量级。
倍频程:可闻声的频率为20-20 000Hz ,范围较宽,变化较大。
为了方便起见,将这个频率带宽划分为几个频率段,称为频段或频程。
每个频程的中心频率为该频段上下限频率的比例中项,即210f f f =1、 何为实时处理、何为在线测量?实时处理:指在测量过程中要求立刻得到测量结果。
意思是不舍弃观测信号,其处理时间能跟上信号变化的需要,或者说信号处理的速度能跟上信号变化的速度;在线测量:不停机,在系统运行过程中监视或测量某些动态参数;3、传感器动态补偿解决传感器的什么问题?提高传感器动态响应的快速性。
5、频响函数与传递函数有何区别与联系?传递函数,频率响应函数均是描述线性系统动态特性的基本数学工具之一,都是建立在传递函数的基础之上。
但传递函数是系统的物理参数,也就是它受硬件决定,不会随着输入变化而变化,是分析系统的一个数学公式,而频率响应函数是输出函数,也就是说系统的传递函数乘上输入的信号,而得到的频率响应函数(当然是在频域中分析)。
7、仪表的抗干扰技术有哪些?各种抑制干扰噪声的技术和方法可以归纳为3类:一是抑制干扰源的噪声,二是消除或切断干扰噪声的耦合途径,三是对敏感的检测电路采取抗干扰措施。
下面列出一些常用的抗干扰方法:(1)抑制干扰源的噪声①如果允许,就将干扰源围闭在屏蔽罩内;②对噪声源的出线进行滤波;③限制干扰源脉冲的上升沿和下降沿的斜率;④用压敏电阻或其他措施抑制干扰源电感线圈的浪涌电压;⑤将产生噪声的导线与地线绞合在一起;⑥对产生噪声的导线采取屏蔽措施;⑦用于抑制电磁辐射的干扰源屏蔽层要两端接地。
(2)消除或切断干扰噪声的耦合途径①微弱信号线越短越好,而且要远离干扰导线;②低电平信号线采用双绞线或贴近地线放置;③信号线加屏蔽(高频信号线采用同轴电缆),伸出屏蔽层的信号线端越短越好;④用于保护低电平信号线的屏蔽层要单点接地,同轴电缆用于高频要将屏蔽层两端接地,电路系统也要单点接地,高频电路就近接板地;⑤对敏感电路要加屏蔽罩,进入该屏蔽罩的任何其他导线都要加滤波和去耦措施;⑥如果低电平信号端子和带有干扰噪声的端子处于同一个连接器中,在它们之间放置地线端子;⑦低电平电路和高电平电路避免使用公共地线;⑧电路接地线和设备接地线要分开;⑨接地线越短越好,避免地线形成环状;⑩微弱信号检测要采用差动放大电路,电路的信号源和负载对地阻抗要平衡;○11采用隔离措施,避免地电位差耦合到信号电路。
(3)检测电路的其他抗干扰措施①检测电路的通频带宽度要尽可能窄,尽量使用选频滤波;②直流电源线一定要加去耦滤波,滤波电解电容要用高频小电容旁路,各部分电路的电源滤波电容应尽量靠近该电路;③信号地线、其他可能造成干扰的电路地线以及设备地线要分开;④使用屏蔽罩。
9、什么是频率混叠?什么是功率泄露?各自如何避免?当用采样频率F对一个信号进行采样时,信号中F/2以上的频率不是消失了,而是对称的映象到了F/2以下的频带中,并且和F/2以下的原有频率成分叠加起来,这个现象叫做“混叠”。
消除混叠的方法有两种:1.提高采样频率F,即缩小采样时间间隔.然而实际的信号处理系统不可能达到很大的采样频率,处理不了很多的数据.另外,许多信号本身可能含有全频带的频率成分,不可能将采样频率提高到无穷大.所以,通过采样频率避免混叠是有限制的.2.采用抗混叠滤波器.在采用频率F 一定的前提下,通过低通滤波器滤掉高于F/2的频率成分,通过低通滤波器的信号则可避免出现频率混叠.(信号泄漏)对于有限长信号样本进行傅里叶分析时,相当于将无限长的信号乘以有限宽的窗函数,由此导致的误差称为泄漏。
增大截断长度会使泄漏误差减小,理论上如果不截断就不会产生泄漏误差;对于周期函数而言,样本长度T等于信号周期 的整倍数,将不产生泄漏问题,否则仍产生泄漏。
一般而言,可以通过采用特地设计的窗函数来截取信号,可以减小泄漏误差。
13、说明传感器灵敏度标定的实验基本过程。
15、傅里叶分析如何提高频率分辨率的?请给出傅里叶分析的基本步骤。
能够提高频率分辨率的方法即为选带傅里叶分析(BSFA )。
即在所选择的频带*∆f ()21f f f -=∆* 内,进行与基带分析有同样多的谱线的分析。
从而能大大提高频率分辨率。
选带分析时频率分辨率为//12/2s s f f f f n T n n n **∆∆∆====⋅∆ (2)选带傅氏分析(细化)的主要步骤是:(a) 输入信号先经模拟抗混滤波,滤去所需分析的最高频率max f (基带分析中的最高分析频率)以上的频率成分;(b) 经过模数转换,变为数字信号序列{}r x 1,2,3,(1)r Mn =-,M为细化倍数,n 为变换规模,例如1K 的FFT 变换,n =1024,由于采样量变为Mn ,从而采样时间(或信号记录长度)也应为MT,T为基带分析时的采样时间;(c) 将采样信号经数字移频,即乘以tr f j k e ∆-π2,移频后的k f 处的谱线将落在频率轴上的零频处;(d) 将移频后的数字信号再经数字低通滤波,滤去所需频带以外的信号; (e) 对滤波后的信号的时间序列进行重采样,采样频率为M f f s s // ,即每隔M个点抽取一个样,送入处理机进行 FFT 。
事实上,重采样的采样量仍为n (如1024),但采样的时间加长了M倍。
17、。