excel正交试验设计模板 -回复
- 格式:doc
- 大小:14.45 KB
- 文档页数:3

第一题考察温度对烧碱产品得率的影响,选了四种不同温度进行试验,在同一温度下进行了5次试验(三数据见下表)。
希望在显着性水平为0.05。
1.SSE的公式2.SSA的公式3.将表格粘贴进Excel,然后进行数据分析,勾选标于第一行,显示在下面P=0.001799,远小于0.05,所以是显着的4.打开Minitab,复制表格,“统计”“方差分析”“选单因素未重叠”“响应C1C2C3C4”点击“比较”勾选第一个,确定结果: 工作表 3单因子方差分析: 60度, 65度, 70度, 75度来源自由度 SS MS F P因子 3 84.15 28.05 7.96 0.002误差 16 56.40 3.52合计 19 140.55S = 1.877 R-Sq = 59.87% R-Sq(调整) = 52.35%平均值(基于合并标准差)的单组 95% 置信区间水平 N 平均值标准差 ------+---------+---------+---------+---60度 5 90.200 1.789 (------*------)65度 5 93.200 1.789 (------*------)70度 5 95.000 2.000 (------*------)75度 5 90.200 1.924 (------*------)------+---------+---------+---------+---90.0 92.5 95.0 97.5合并标准差 = 1.877Tukey 95% 同时置信区间所有配对比较单组置信水平 = 98.87%60度减自:下限中心上限 ------+---------+---------+---------+---65度 -0.401 3.000 6.401 (------*------)70度 1.399 4.800 8.201 (------*-----)75度 -3.401 0.000 3.401 (------*------)------+---------+---------+---------+----5.0 0.0 5.0 10.065度减自:下限中心上限 ------+---------+---------+---------+---70度 -1.601 1.800 5.201 (------*-----)75度 -6.401 -3.000 0.401 (------*------)------+---------+---------+---------+----5.0 0.0 5.0 10.070度减自:下限中心上限 ------+---------+---------+---------+---75度 -8.201 -4.800 -1.399 (-----*------)------+---------+---------+---------+----5.0 0.0 5.0 10.0获得结果,区间相交包含0.0的不明显,反之明显第二题为研究线路板焊点拉拔力与烘烤温度、烘烤时间和焊剂量之间关系。

《试验设计与数据处理》课程思政探索与实践发布时间:2023-03-16T08:22:04.426Z 来源:《中国科技信息》2022年10月第20期作者:冯振, 陈丰君,陈贺贺[导读] 在深化新时代学校思想政治理论改革创新的背景下,冯振, 陈丰君,陈贺贺河南工学院材料科学与工程学院,河南新乡 453003摘要:在深化新时代学校思想政治理论改革创新的背景下,本文针对我校材料类专业的基础必修课程《试验设计与数据处理》,通过分析本课程的课程思政教学现状,从课程思政建设策略、教学方法、考核方式等方面对本课程的课程思政建设进行探索与实践。
关键词:课程思政;试验设计与数据处理;教学实践;教学改革习近平总书记在全国高校思想政治工作会议上明确指出:“高校立身之本在于立德树人”、“要坚持把立德树人作为中心环节,把思想政治工作贯穿教育教学全过程,实现全程育人、全方位育人,努力开创我国高等教育事业发展新局面”[1]。
《试验设计与数据处理》该学科涉及到化学、数学、统计学、计算机等多门学科,内容涵盖方案的优化、理论公式的推导和计算、试验结果的统计与分析以及计算机软件的应用。
内容多、公式多、计算多等特点,决定了该课程本身的繁杂性[2]。
如何把课程思政教育“立德树人”这一理念融入这门课程的教学工作过程中是个难点,本文针对这一问题进行探索、实践和总结分析。
1 试验设计与数据处理课程思政目标试验设计与数据处理虽然归于数理统计的范畴,但它也属于应用技术学科,具有很强的实用性[3]。
实施试验设计与数据处理课程思政的目的在于:一是使学生掌握试验设计与数据分析的基本原理和基本方法;二是使学生掌握试验设计(正交设计、均匀设计、配方设计)及数据分析(误差分析、直观分析、方差分析、回归分析)等内容,并具备熟练运用Excel进行数据分析的能力;三是要求教师在教学过程中注重提升课程思政意识和职业素养,在传授课程知识的同时,充分挖掘该课程中的思政元素,培养学生树立正确的三观,努力做到“全员育人、全程育人、全方位育人”,提升学生的知识、素质和能力。

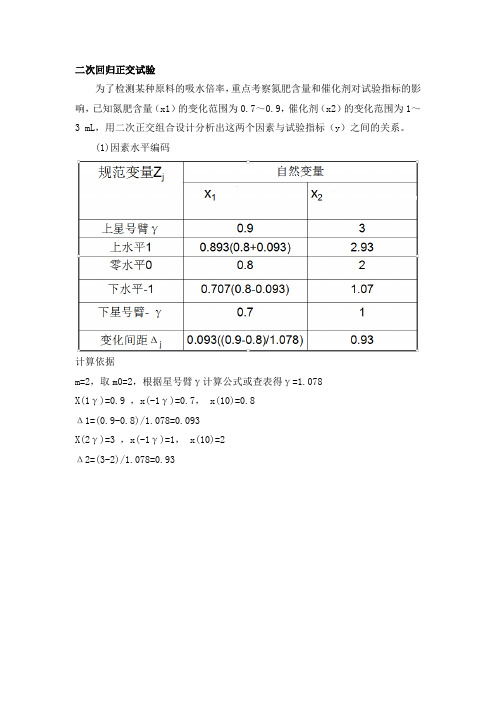
二次回归正交试验为了检测某种原料的吸水倍率,重点考察氮肥含量和催化剂对试验指标的影响,已知氮肥含量(x1)的变化范围为0.7~0.9,催化剂(x2)的变化范围为1~3 mL,用二次正交组合设计分析出这两个因素与试验指标(y)之间的关系。
(1)因素水平编码计算依据m=2,取m0=2,根据星号臂γ计算公式或查表得γ=1.078X(1γ)=0.9 ,x(-1γ)=0.7, x(10)=0.8Δ1=(0.9-0.8)/1.078=0.093X(2γ)=3 ,x(-1γ)=1, x(10)=2Δ2=(3-2)/1.078=0.93(2)试验方案(3)回归方程的建立借助excel分析如下:①回归方程显著性检验:F=186.5564,,,12.4)74(95.0=F因此回归方程非常显著。
'74.41'37.2375.656.2609.952.468y 212121z z z z z z ----+= ②偏回归系数的显著性检验9.496.113305.113806.113308.47058.14583.1822.44615.5528.4705701.274.41)(8.1458701.224.23)(3.182475.6)(2.4461324.656.265.552324.609.95.113801046852206303)(12211122122122222222112111122121212122212222221121122121=-=-==++++=++++==⨯===⨯===⨯===⨯===⨯===-=-=∑∑∑∑∑∑∑=======R T e R ni in i i ni ni i n i in i i n i iT SS SS SS SS SS SS SS SS SS z b SS zb SS z z b SS z b SS z b SS y n y SS 方差分析:dfT=n-1=10-1=9 df1=df2=df12=df1’=df2’=1dfR=df1+df2+df12+df1’+df2’=1+1+1+1+1=5dfe=dfT-dfR=9-5=4MS1=522.5/1=522.5 MS2=SS2/df2=4461.2/1=4461.2 MS12=SS12/df12=182.3MS1’=SS1’/df1’=1458.8MS2’=SS2’/df1’=4705.8MSR=SSR/dfR=11330.6/5=2266.1MSe=SSe/dfe=49.9/4=12.5F1=MS1/MSe=522.5/12.5=41.8F2=MS2/MSe=4461.2/12.5=356.9F12=MS12/MSe=182.3/12.5=14.6F1’=MS1’/MSe=1458.8/12.5=116.7F2’=MS2’/MSe=4705.8/12.5=376.5FR=MSR/MSe=2266.1/12.5=181.3F0.01(1,4)=21.20 F0.05(1,4)=7.71 F0.01(5,4)=15.52 F0.05(5,4)=6.26失拟性检验本例零水平试验次数m0=2,可进行失拟性检验5.45.521220521225)509512(21)259081262144()(12201020101=-=+-+=-=∑∑==m i i m i ie y m y SSSSLf=SSe-SSe1=49.9-4.5=45.4 dfe1=m0-1=2-1=1 dfLf=dfe-dfe1=4-1=359.53)1,3(37.31/5.43/5.45/1/1,01====F df SSe df SS FLf e LfLf检验结果表明,失拟不显著,回归模型与实际情况拟合很好。


excel正交试验设计模板
在Excel中,可以使用一些功能和技巧来创建正交试验设计模板。
以下是一种常见的方法:
步骤1,打开Excel并创建一个新的工作表。
步骤2,确定需要设计的因素和水平数。
例如,假设有3个因素,每个因素有2个水平。
步骤3,创建因素和水平的标签。
在第一行输入因素的名称,例如A、B、C,然后在下面的行中输入每个因素的水平标签,例如A1、A2、B1、B2、C1、C2。
步骤4,确定正交表的大小。
正交表的大小应为因素数的幂,且大于或等于水平数。
在本例中,因素数为3,水平数为2,因此正交表的大小应为4。
步骤5,使用Excel的数据验证功能创建正交表格。
选择一个合适的单元格作为正交表的起始位置,然后按照正交表的大小创建一个矩形区域。
在选定的单元格上,依次选择“数据”>“数据验
证”>“列表”,并输入因素的水平标签作为验证的源。
步骤6,填充正交表格。
将正交表格的起始位置设置为公式,然后使用填充功能将该公式应用到整个正交表格区域。
步骤7,根据需要调整格式和布局。
可以使用Excel的格式化功能来调整正交表格的外观,例如设置边框、添加颜色等。
步骤8,保存和使用正交试验设计模板。
将工作表保存为Excel 模板文件,以便以后可以重复使用。
以上是创建Excel正交试验设计模板的基本步骤。
根据实际需求,你还可以进一步自定义和扩展该模板,例如添加响应变量、计算统计指标等。
希望这些信息能对你有所帮助!。
excel正交试验设计模板-回复
Excel正交试验设计模板
正交试验设计是一种经典的实验设计方法,用于确定影响某个响应变量的关键因素及其相互作用。
在Excel中,我们可以利用自带的数据分析工具和函数来实现正交试验设计。
本文将一步一步回答关于Excel正交试验设计模板的问题。
1. 什么是正交试验设计?
正交试验设计是一种优化的实验设计方法,通过系统地排列和组合一系列因素,以确定对某个响应变量具有最大影响的关键因素及其相互作用。
正交试验设计的特点是能够有效地减少实验次数,并提高实验效果。
2. Excel中如何创建正交试验设计表?
首先,在Excel中创建一个新的工作表。
将待测试的因素列出,分别创建一列作为因素的变量名。
然后,根据正交试验设计的要求,在其他列中填写因素的不同水平。
最后,使用Excel的数据分析工具或函数生成正交试验设计表。
3. 如何使用Excel的数据分析工具生成正交试验设计表?
Excel提供了多种数据分析工具,其中的“数据分析工具包”是一个常用
的插件。
首先,点击Excel菜单栏中的“数据”选项卡,在“分析”选项中选择“数据分析”。
接着,在弹出的对话框中选择“正交试验设计”,并点击“确定”。
在正交试验设计对话框中,依次填写相关参数。
首先,选择“设计类型”,根据实验要求选择正交试验设计的类型,如正交表、正交数组等。
然后,选择“因素个数”,填写待测试的因素个数。
接着,选择“水平数”,填写每个因素的水平数。
最后,点击“确定”。
Excel将自动生成一张正交试验设计表,其中每列代表一个因素,每行代表一组试验条件,而设计表中的数值则表示每个因素的不同水平。
这样,我们就可以根据设计表中的试验条件进行实验,并记录相应的响应变量。
4. 如何通过Excel函数生成正交试验设计表?
Excel中的函数也可以用于生成正交试验设计表。
常用的函数包括
“=RAND()”和“=RANK()”。
首先,在一个空白单元格中输入
“=RAND()”函数,并复制到设计表的每个单元格,以生成一组随机数。
然后,选择设计表中的每列数据,使用“数据”选项中的“排序”功能,按照从小到大的顺序对每列数据进行排序。
接着,在设计表的每一列旁边创建一列,使用“=RANK()”函数对每列数据进行排序。
最后,将设计表中的每一列按照顺序分别替换为1、2、3、...、n(n为水平数),即可得到正交试验设计表。
此时,每列的数值代表了对应因素的不同水平。
通过这样的设计表,我们可以进行正交试验,并记录相应的响应变量。
5. 如何分析正交试验结果?
通过正交试验设计得到的实验数据,可以利用Excel的数据分析工具或相关函数进行分析。
常用的数据分析方法有方差分析、回归分析等。
例如,在Excel中进行方差分析,可先将实验数据输入到一个单独的工作表中。
点击Excel菜单栏中的“数据”选项卡,在“数据分析”中选择“方差分析”。
在方差分析对话框中,选择适当的参数,如因子数、水平数等,并点击“确定”。
Excel将自动生成方差分析结果,包括方差分析表、总体平均、组间变异、组内变异等统计指标。
通过对正交试验结果的方差分析,可以判断不同因素及其相互作用对响应变量的影响程度,进而确定影响效果最显著的因素和水平。
通过以上步骤,我们可以在Excel中使用正交试验设计模板来进行实验设计和分析。
正交试验设计可以极大地提高实验效率,帮助我们快速确定关键因素和优化实验方案,为工程和科研提供有力的支持。