安徽省舒城一中2017年高考仿真卷理科数学(四)

2017年高考数学模拟试题(全国新课标卷)含解析(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017年高考数学模拟试题(全国新课标卷)含解析(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017年高考数学模拟试题(全国新课标卷)含解析(word版可编辑修改)的全部内容。

2017年高考模拟数学试题（全国新课标卷）本试卷分第Ⅰ卷(选择题)和第Ⅱ卷（非选择题)两部分。

共150分.考试时间120分钟．第Ⅰ卷一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．i 为虚数单位,复数ii++13= A ．i +2 B ．i -2 C ．2-i D ．2--i 2．等边三角形ABC 的边长为1，如果,,,BC a CA b AB c ===那么a b b c c a ⋅-⋅+⋅等于A ．32B ．32-C ．12D ．12-3．已知集合}4|4||{2<-∈=x x Z x A ，}8121|{≥⎪⎭⎫⎝⎛∈=+yN y B ，记A card 为集合A 的元素个数，则下列说法不正确．．．的是 A ．5card =A B ．3card =B C ．2)card(=B A D ．5)card(=B A 4．一个体积为12错误!的正三棱柱的三视图如图所示， 则该三棱柱的侧视图的面积为A ．6，3B ．8C ．8错误!D ．125．过抛物线24y x =的焦点作直线交抛物线于点()()1122,,,P x y Q x y 两点,若126x x +=，则PQ 中点M 到抛物线准线的距离为A ．5B ．4C ．3D ．2 6．下列说法正确的是A ．互斥事件一定是对立事件，对立事件不一定是互斥事件B ．互斥事件不一定是对立事件，对立事件一定是互斥事件C ．事件A 、B 中至少有一个发生的概率一定比A 、B 中恰有一个发生的概率大D ．事件A 、B 同时发生的概率一定比A 、B 中恰有一个发生的概率小7．如图是秦九韶算法的一个程序框图，则输出的S 为A ．1030020(())a x a x a a x +++的值B ．3020100(())a x a x a a x +++的值C ．0010230(())a x a x a a x +++的值D ．2000310(())a x a x a a x +++的值8．若（9x －错误!）n(n ∈N ＊)的展开式的第3项的二项式系数为36，则其展开式中的常数项为 A ．252 B ．－252 C ．84 D ．－84 9．若S 1＝错误!错误!d x ,S 2＝错误!（ln x ＋1)d x ，S 3＝错误!x d x ,则S 1,S 2，S 3的大小关系为 A ．S 1＜S 2＜S 3 B ．S 2＜S 1＜S 3 C ．S 1＜S 3＜S 2 D ．S 3＜S 1＜S 210．在平面直角坐标系中,双曲线221124x y -=的右焦点为F ,一条过原点O 且倾斜角为锐角的直线l 与双曲线C 交于A ,B 两点。

安徽省舒城县2017届高三数学仿真试题（三）理时间：120分钟 总分：150分一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设集合2{|60}A x x x =-≤-，22{|}B x x >=，则A B ⋂=（ ）（A ）(2,3]（B ）(2,3)（C ）(2,3]-（D ）(2,3)-（ ）（A ）1-（B ）0（C ）1（D ）23.在ABC ∆中，角A B C 、、的对边分别为a b c 、、，则“sin sin A B >”是“a b >”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ． 即不充分也不必要条件4.设函数f (x )＝ax ＋bx 2＋c的图象如图，则a ，b ，c 满足（ ）A ．a >b >cB ．a >c >bC ．b >a >cD ．b >c >a5.在△ABC 中，点D 是BC 的中点，点E 是AC 的中点，点F 在线段AD 上并且│AF │ = 2│DF │，设AB u u u r=a ，BC u u u r =b ，则EF u u u r=（ ）A ．23a 16-bB ．23a 12- bC ．16a 13- bD ．16a 16-b6. 设点A 为双曲线C ：22221(0x y a a b -=>，0)b >的一个顶点，点A 到双曲线C 的一条渐近线的距离为2b，则双曲线的离心率是 （ ）A ．2B ．3C ．23D ． 27 .执行如图所示的框图，若输出的sum 的值为2047，则条件框中应填写的是霍山中学高三理数 第1页 (共6页)（ ）A ．9<i ？B ．10<i ？ C. 11<i ？ D ．12<i ？8.已知8,,,221--a a 成等差数列，8,,,,2321--b b b 成等比数列，则212b a a -等于（ ）A ．41B ．21C ．21-D ．21或21- 9.已知()6332z y x ++的展开式中，系数为有理数的项的个数为（ ） A ．4B ．5C.6D ．710.如图，网格上小正方形的边长为1，粗线画出的是某个多面体的三视图，若该多面体的所有顶点都在球O 表面上，则球O 的表面积是（ ）A ．π36B ．π48 C.π56 D ．π642i11.已知锐角βα、满足2cos sin cos sin <+αββα，设()x x f a a log ,tan tan =⋅=βα，则下列判断正确的是（ ）A ．()()βαcos sin f f >B ．()()βαsin cos f f > C.()()βαsin sin f f >D ．()()βαcos cos f f >12.设函数()f x = x ·e x，2()2g x x x =+，2()2sin()63h x x =+ππ，若对任意的x ∈R ，都有()()[()2]k h x g x x f ≤+-成立，则实数k 的取值范围是 （ ）A ．1(,1]e-∞+B ．1(2,3]e -+C ．e1[2,)++∞D ．e 1[1,)++∞二、填空题：本大题共4小题，每小题5分．13.已知命题:p 若b a <，则22bc ac <，命题。

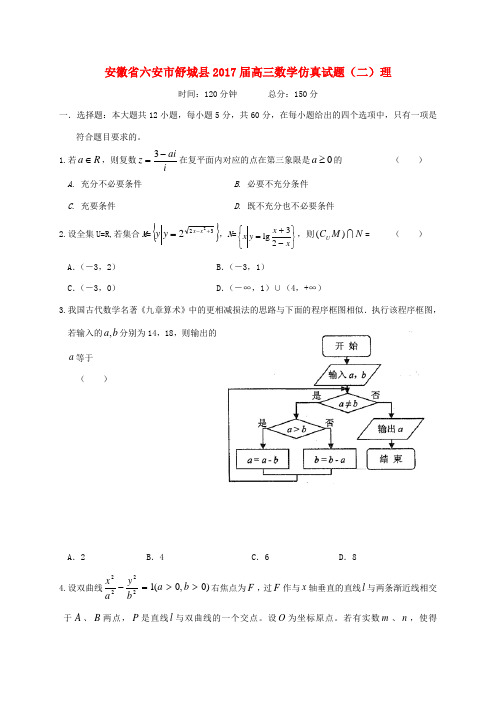
安徽省六安市舒城县2017届高三数学仿真试题（二）理时间：120分钟 总分：150分一．选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1.若R a ∈，则复数iaiz -=3在复平面内对应的点在第三象限是0a ≥的 （ ）A. 充分不必要条件 B . 必要不充分条件 C . 充要条件D . 既不充分也不必要条件2.设全集U=R,若集合M ={}3222+-=x x y y ，N =⎭⎬⎫⎩⎨⎧-+=x x y x 23lg ，则N M C U )(=（ ）A ．（－3，2）B ．（－3，1）C ．（－3，0）D ．（－∞，1）∪（4，+∞）3.我国古代数学名著《九章算术》中的更相减损法的思路与下面的程序框图相似．执行该程序框图，若输入的,a b 分别为14，18，则输出的a 等于（ ）A ．2B ．4C ．6D ．84.设双曲线)0,0(12222>>=-b a by ax 右焦点为F ，过F 作与x 轴垂直的直线l 与两条渐近线相交于A 、B 两点，P 是直线l 与双曲线的一个交点。

设O 为坐标原点。

若有实数m 、n ，使得OB n OA m OP +=，且92=mn ，则该双曲线的离心率为 （ ）A.423 B.89C.553 D.223 5. 某几何体的三视图如图所示，则这个几何体的体积为( )A. 4B.203 C. 263 D. 8 6. 设k 是一个正整数，在1+)k x k （的展开式中，第四项的系数为116，记函数2y x = 与y kx =的图象所围成的阴影部分面积为S ，任取[0,4]x ∈，[0,16]y ∈，则点(,)x y 恰好落在阴影区域S 内的概率是（ ）A ．23 B ．13C ．25 D ．167. 设0.50.82x =,2log y =sin1z =。

则x 、y 、z 的大小关系为（ ）A.z y x <<B.x z y <<C.y x z <<D.x y z <<8．若实数y x ,满足不等式组330101x y x y y +-≤⎧⎪-+≥⎨⎪≥-⎩，，，则2||z x y =+的取值范围是（ ）A ．[1,3]- B.[1,11]C.]3,1[D.]11,1[-9. 设函数1463)(23+++=x x x x f 且19)(,1)(==b f a f 。

安徽省舒城县2017届高三数学仿真试题（三）理时间：120分钟 总分：150分一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设集合2{|60}A x x x =-≤-，2{}B x >=，则A B ⋂=（ ）（A ）(2,3]（B ）(2,3)（C ）(2,3]-（D ）(2,3)-（ ）（A ）1-（B ）0（C ）1（D ）23.在ABC ∆中，角A B C 、、的对边分别为a b c 、、，则“sin sin A B >”是“a b >”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ． 即不充分也不必要条件4.设函数f (x )＝ax ＋bx 2＋c的图象如图，则a ，b ，c 满足（ ）A ．a >b >cB ．a >c >bC ．b >a >cD ．b >c >a5.在△ABC 中，点D 是BC 的中点，点E 是AC 的中点，点F 在线段AD 上并且│AF │ = 2│DF │，设AB =a ，BC =b ，则EF =（ ）A ．23a 16-bB ．23a 12- bC ．16a 13- bD ．16a 16-b6. 设点A 为双曲线C ：22221(0x y a a b-=>，0)b >的一个顶点，点A 到双曲线C 的一条渐近线的距离为2b，则双曲线的离心率是 （ ）A ．2B ．3C ．23D ． 27 .执行如图所示的框图，若输出的sum 的值为2047，则条件框中应填写的是霍山中学高三理数 第1页 (共6页)（ ）A ．9<i ？B ．10<i ？ C. 11<i ？ D ．12<i ？8.已知8,,,221--a a 成等差数列，8,,,,2321--b b b 成等比数列，则212b a a -等于（ ）A ．41 B ．21C ．21-D ．21或21- 9.已知()6332z y x ++的展开式中，系数为有理数的项的个数为（ ） A ．4B ．5C.6D ．710.如图，网格上小正方形的边长为1，粗线画出的是某个多面体的三视图，若该多面体的所有顶点都在球O 表面上，则球O 的表面积是（ ）A ．π36B ．π48 C.π56 D ．π642i11.已知锐角βα、满足2cos sin cos sin <+αββα，设()x x f a a log ,tan tan =⋅=βα，则下列判断正确的是（ ）A ．()()βαcos sin f f >B ．()()βαsin cos f f > C.()()βαsin sin f f >D ．()()βαcos cos f f >12.设函数()f x = x ·e x，2()2g x x x =+，2()2sin()63h x x =+ππ，若对任意的x ∈R ，都有()()[()2]k h x g x x f ≤+-成立，则实数k 的取值范围是（ ）A ．1(,1]e-∞+B ．1(2,3]e -+C ．e1[2,)++∞D ．e 1[1,)++∞二、填空题：本大题共4小题，每小题5分．13.已知命题:p 若b a <，则22bc ac <，命题。

安徽省2017年高考理科数学试题及答案(word版)1.已知集合A={x|x<1}，B={x|3x<1}，求B的取值范围。

A。

B={x|x<0}B。

B={x|x>1}C。

B=AD。

B=R解析：将3x<1化简得x<1/3，所以B={x|x<1/3}，选项A 为正确答案。

2.如图，正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是多少？A。

1/4B。

π/8C。

1/2D。

π/4解析：由于黑色部分和白色部分关于正方形的中心成中心对称，所以黑色部分的面积等于白色部分的面积，即黑色部分的面积为正方形面积的一半。

所以此点取自黑色部分的概率为1/2，选项C为正确答案。

3.设有下面四个命题：p1：若复数z满足Re(z)=0，则z∈R；p2：若复数z满足z2∈R，则z∈R；p3：若复数z1,z2满足z1z2∈R，则z1=z2；p4：若复数z∈R，则z∈R。

其中的真命题为？A。

p1,p3B。

p1,p4C。

p2,p3D。

p2,p4解析：p1显然是真命题，因为实数的虚部为0.对于p2，设z=a+bi，则z2=a2-b2+2abi，z2∈R意味着b=0，即z∈R。

所以p2也是真命题。

对于p3，设z1=a1+b1i，z2=a2+b2i，则z1z2=(a1a2-b1b2)+(a1b2+a2b1)i，z1z2∈R意味着a1b2+a2b1=0，即z1/z2为纯虚数，所以z1=z2.所以p3也是真命题。

对于p4，显然是真命题。

所以选项B为正确答案。

4.记Sn为等差数列{an}的前n项和。

若a4+a5=24，S6=48，则{an}的公差为多少？A。

1B。

2C。

4D。

8解析：设等差数列的公差为d，则a4=a1+3d，a5=a1+4d，S6=3a1+15d=48，a4+a5=2a1+7d=24.解得a1=4，d=4，所以公差为4，选项C为正确答案。

安徽省舒城县2017届高三数学仿真试题（三）理时间：120分钟 总分：150分一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设集合2{|60}A x x x =-≤-，2{}B x >=，则A B ⋂=（ ）（A ）(2,3]（B ）(2,3)（C ）(2,3]-（D ）(2,3)-（ ）（A ）1-（B ）0（C ）1（D ）23.在ABC ∆中，角A B C 、、的对边分别为a b c 、、，则“sin sin A B >”是“a b >”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ． 即不充分也不必要条件4.设函数f (x )＝ax ＋bx 2＋c的图象如图，则a ，b ，c 满足（ ）A ．a >b >cB ．a >c >bC ．b >a >cD ．b >c >a5.在△ABC 中，点D 是BC 的中点，点E 是AC 的中点，点F 在线段AD 上并且│AF │ = 2│DF │，设AB =a ，BC =b ，则EF =（ ）A ．23a 16-bB ．23a 12- bC ．16a 13- bD ．16a 16-b6. 设点A 为双曲线C ：22221(0x y a a b -=>，0)b >的一个顶点，点A 到双曲线C 的一条渐近线的距离为2b，则双曲线的离心率是 （ ）A ．2B ．3C ．23D ． 27 .执行如图所示的框图，若输出的sum 的值为2047，则条件框中应填写的是霍山中学高三理数 第1页 (共6页)（ ）A ．9<i ？B ．10<i ？ C. 11<i ？ D ．12<i ？8.已知8,,,221--a a 成等差数列，8,,,,2321--b b b 成等比数列，则212b a a -等于（ ）A ．41 B ．21C ．21-D ．21或21- 9.已知()6332z y x ++的展开式中，系数为有理数的项的个数为（ ） A ．4B ．5C.6D ．710.如图，网格上小正方形的边长为1，粗线画出的是某个多面体的三视图，若该多面体的所有顶点都在球O 表面上，则球O 的表面积是（ ）A ．π36B ．π48 C.π56 D ．π642i11.已知锐角βα、满足2cos sin cos sin <+αββα，设()x x f a a log ,tan tan =⋅=βα，则下列判断正确的是（ ）A ．()()βαcos sin f f >B ．()()βαsin cos f f > C.()()βαsin sin f f >D ．()()βαcos cos f f >12.设函数()f x = x ·e x，2()2g x x x =+，2()2sin()63h x x =+ππ，若对任意的x ∈R ，都有()()[()2]k h x g x x f ≤+-成立，则实数k 的取值范围是 （ ）A ．1(,1]e-∞+B ．1(2,3]e -+C ．e1[2,)++∞D ．e 1[1,)++∞二、填空题：本大题共4小题，每小题5分．13.已知命题:p 若b a <，则22bc ac <，命题2000:0,ln 1q x x x ∃>-=。

2017年安徽省六安市舒城中学高考数学仿真试卷（理科）（二）一．选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．若a∈R，则复数z=在复平面内对应的点在第三象限是a≥0的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件2．设全集U=R，若集合M={y|y=}，N={x|y=lg}，则（C U M）∩N=（）A．（﹣3，2）B．（﹣3，0）C．（﹣∞，1）∪（4，+∞）D．（﹣3，1）3．我国古代数学名著《九章算术》中的更相减损法的思路与图相似．执行该程序框图，若输入的a，b分别为14，18，则输出的a=（）A．2 B．4 C．6 D．84．设双曲线右焦点为F，过F作与x轴垂直的直线l与两条渐近线相交于A、B两点，P是直线l与双曲线的一个交点．设O为坐标原点．若有实数m、n，使得，且，则该双曲线的离心率为（）A．B．C．D．5．某几何体的三视图如图所示，则这个几何体的体积为（）A．4 B．8 C．D．6．设k是一个正整数，（1+）k的展开式中第四项的系数为，记函数y=x2与y=kx的图象所围成的阴影部分为S，任取x∈，y∈，则点（x，y）恰好落在阴影区域内的概率为（）A．B．C．D．7．设x=0.820.5，，z=sin1．则x、y、z的大小关系为（）A．x＜y＜z B．y＜z＜x C．z＜x＜y D．z＜y＜x8．若实数x，y满足不等式组则z=2|x|+y的取值范围是（）A． B． C． D．9．设函数f（x）=x3+3x2+6x+14且f（a）=1，f（b）=19．则a+b=（）A．2 B．1 C．0 D．﹣210．设曲线f（x）=Asin（x+θ）（A＞0）的一条对称轴为，则曲线的一个对称点为（）A．B．C．D．11．已知θ∈22．极坐标系中椭圆C的方程为ρ2=，以极点为原点，极轴为x轴非负半轴，建立平面直角坐标系，且两坐标系取相同的单位长度．（1）若椭圆上任一点坐标为P（x，y），求的取值范围；（2）若椭圆的两条弦AB，CD交于点Q，且直线AB与CD的倾斜角互补，求证：|QA|•|QB|=|QC|•|QD|．23．已知函数，x∈R．（1）证明对∀a、b∈R，且a≠b，总有：|f（a）﹣f（b）|＜|a﹣b|；（2）设a、b、c∈R，且，证明：a+b+c≥ab+bc+ca．2017年安徽省六安市舒城中学高考数学仿真试卷（理科）（二）参考答案与试题解析一．选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．若a ∈R ，则复数z=在复平面内对应的点在第三象限是a ≥0的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【考点】2L ：必要条件、充分条件与充要条件的判断．【分析】利用复数的运算法则、不等式的解法、几何意义即可得出．【解答】解：复数z===﹣3i ﹣a 在复平面内对应的点（﹣a ，﹣3）在第三象限，∴，解得a ＞0．∴复数z=在复平面内对应的点在第三象限是a ≥0的充分不必要条件．故选：A ．2．设全集U=R ，若集合M={y|y=}，N={x|y=lg }，则（C U M ）∩N=（ ） A ．（﹣3，2）B ．（﹣3，0）C ．（﹣∞，1）∪（4，+∞）D ．（﹣3，1）【考点】48：指数函数的定义、解析式、定义域和值域；1H ：交、并、补集的混合运算；4K ：对数函数的定义域．【分析】由集合的意义，可得M 为函数y=的值域，N 为函数y=lg的定义域；对于M ，先求t=2x ﹣x 2+3的范围，再求得0≤≤2，进而可得y=的值域，即可得集合M ，由补集的定义可得C U M ；对于N ，由对数函数的定义域可得集合N ，由集合的运算计算可得答案．【解答】解：由集合的意义，可得M为函数y=的值域，令t=2x﹣x2+3，t≥0，由二次函数的性质可得t=﹣x2+2x+3=﹣（x﹣1）2+4，易得t≤4，则0≤t≤4，进而可得0≤≤2；在y=中，有1≤y≤4；即M={y|1≤y≤4}，则（C U M）={y|y＜1或y＞4}；集合N为函数y=lg的定义域，则＞0，解可得﹣3＜x＜2，即N={x|﹣3＜x＜2}；则（C U M）∩N={x|﹣3＜x＜1}=（﹣3，1）；故选D．3．我国古代数学名著《九章算术》中的更相减损法的思路与图相似．执行该程序框图，若输入的a，b分别为14，18，则输出的a=（）A．2 B．4 C．6 D．8【考点】EF：程序框图．【分析】由循环结构的特点，先判断，再执行，分别计算出当前的a，b的值，即可得到结论．【解答】解：由a=14，b=18，a＜b，则b变为18﹣14=4，由a＞b，则a变为14﹣4=10，由a＞b，则a变为10﹣4=6，由a ＞b ，则a 变为6﹣4=2， 由a ＜b ，则b 变为4﹣2=2， 由a=b=2， 则输出的a=2． 故选：A ．4．设双曲线右焦点为F ，过F 作与x轴垂直的直线l 与两条渐近线相交于A 、B 两点，P 是直线l 与双曲线的一个交点．设O 为坐标原点．若有实数m 、n ，使得，且，则该双曲线的离心率为（ ）A ．B ．C ．D ．【考点】KC ：双曲线的简单性质．【分析】求出A 、C 坐标，然后求出P 的坐标，代入双曲线方程，利用，即可求出双曲线的离心率．【解答】解：由题意可知双曲线右焦点为F （c ，0），渐近线方程y=±x ，则A （c ，），B （c ，﹣），=（（m+n ）c ，（m ﹣n ））代入=（（m+n ）c ，（m ﹣n ）），得P （（m+n ）c ，（m ﹣n ）），代入双曲线方程得﹣=1，由e=，整理得：4e 2mn=1，由，∴e=；故选A．5．某几何体的三视图如图所示，则这个几何体的体积为（）A．4 B．8 C．D．【考点】L!：由三视图求面积、体积．【分析】由已知中的三视图可得：该几何体是一个四棱锥和一个三棱锥组成的组合体，画出几何体的直观图，求出两个棱锥的体积，相加可得答案．【解答】解：由已知中的三视图可得该几何体的直观图如下图所示：该几何体是一个四棱锥A﹣CDEF和一个三棱锥组F﹣ABC成的组合体，四棱锥A﹣CDEF的底面面积为4，高为4，故体积为：，三棱锥组F﹣ABC的底面面积为2，高为2，故体积为：，故这个几何体的体积V=，故选：C．6．设k是一个正整数，（1+）k的展开式中第四项的系数为，记函数y=x2与y=kx的图象所围成的阴影部分为S，任取x∈，y∈，则点（x，y）恰好落在阴影区域内的概率为（）A．B．C．D．【考点】CF：几何概型；6G：定积分在求面积中的应用．【分析】先利用二项式定理求出k值，再利用积分求阴影部分的面积，那积分的上下限由求方程组得到．然后利用几何概型的概率公式解答．【解答】解：根据题意得，解得：k=4或 k=（舍去）解方程组，解得：x=0或4∴阴影部分的面积为=，任取x∈，y∈，则点（x，y）对应区域面积为4×16=64，由几何概型概率求法得点（x，y）恰好落在阴影区域内的概率为；故选C．7．设x=0.820.5，，z=sin1．则x、y、z的大小关系为（）A．x＜y＜z B．y＜z＜x C．z＜x＜y D．z＜y＜x【考点】4M：对数值大小的比较．【分析】利用指数函数与对数函数的单调性、三角函数的单调性即可判断出结论．【解答】解：x=0.820.5=＞=，=，z=sin1＜sin60°=＜0.9．则x、y、z的大小关系为x＞y＞z．故选：D．8．若实数x，y满足不等式组则z=2|x|+y的取值范围是（）A． B． C． D．【考点】7C：简单线性规划．【分析】先画出满足条件的平面区域，通过讨论x的范围，求出直线的表达式，结合图象从而求出z的范围．【解答】解：画出满足条件的平面区域，如图示：，显然x≤0时，直线方程为：y=2x+z，过（0，﹣1）时，z最小，Z最小值=﹣1，x≥0时，直线方程为：y=﹣2x+z，过（6，﹣1）时，z最大，Z最大值=11，故选：D．9．设函数f（x）=x3+3x2+6x+14且f（a）=1，f（b）=19．则a+b=（）A．2 B．1 C．0 D．﹣2【考点】3T：函数的值．【分析】根据f（x）=x3+3x2+6x+14可将f（x）变形为f（x）=（x+1）3+3（x+1）+10然后根据f（a）+f（b）=20可得（a+1）2+3（a+1）+（b+1）2+3（b+1）=0注意到此方程的对称性可构造函数F（x）=x3+3x则上式可变形为F（a+1）=﹣F（b+1）故需判断出函数F（x）的奇偶性和单调性即可求解．【解答】解：∵f（x）=x3+3x2+6x+14∴f（x）=（x+1）3+3（x+1）+10∵f（a）=1，f（b）=19，∴f（a）+f（b）=20∴（a+1）2+3（a+1）+（b+1）2+3（b+1）=0①令F（x）=x3+3x，则F（﹣x）=﹣F（x）∴F（x）为奇函数∴①式可变为F（a+1）=﹣F（b+1）即F（a+1）=F（﹣b﹣1）∵F（x）=x3+3x为单调递增函数∴a+1=﹣b﹣1∴a+b=﹣2，故选：D10．设曲线f（x）=Asin（x+θ）（A＞0）的一条对称轴为，则曲线的一个对称点为（）A．B．C．D．【考点】H2：正弦函数的图象．【分析】由函数f（x）的解析式，求出f（x）的周期，再根据对称轴求出f（x）的对称中心，利用函数的对称性以及图象平移法则，即可求出曲线y=f（﹣x）的一个对称点．【解答】解：函数f（x）=Asin（x+θ）的周期为2π，且f（x）的一条对称轴为x=，∴函数f（x）的一个对称点为（﹣，0），即（﹣，0）；∴函数y=f（﹣x）的一个对称中心为（，0）；又函数y=f（﹣x）的图象可以由函数y=f（﹣x）的图象向右平移单位得到，∴曲线y=f（﹣x）的一个对称点为（+，0），即（，0）．故选：B．11．已知θ∈22．极坐标系中椭圆C的方程为ρ2=，以极点为原点，极轴为x轴非负半轴，建立平面直角坐标系，且两坐标系取相同的单位长度．（1）若椭圆上任一点坐标为P（x，y），求的取值范围；（2）若椭圆的两条弦AB，CD交于点Q，且直线AB与CD的倾斜角互补，求证：|QA|•|QB|=|QC|•|QD|．【考点】Q4：简单曲线的极坐标方程．【分析】（1）由椭圆C的极坐标方程能椭圆C的直角坐标方程，设，由三角函数性质能求出的取值范围．（2）设直线AB的倾斜角为α，直线CD的倾斜角为π﹣α，Q（x0，y0），直线AB的参数方程为，（t为参数），代入x2+2y2=2，得：（x0+tcosα）2+2（y0+tsinα）2﹣2=0，推导出|QA|•|QB|=|t1t2|=||，同理，|QC|•|QB|=||=||，由此能证明|QA|•|QB|=|QC|•|QD|．【解答】（本小题满分10分）选修4﹣4：坐标系与参数方程解：（1）∵椭圆C的方程为ρ2=，∴椭圆C的直角坐标方程为，设，则=．∴的取值范围是．证明：（2）设直线AB的倾斜角为α，直线CD的倾斜角为π﹣α，Q（x0，y0），则直线AB的参数方程为，（t为参数），代入x2+2y2=2，得：（x0+tcosα）2+2（y0+tsinα）2﹣2=0，即（cos2α+2sin2α）t2+（2x0cosα+4y0sinα）t+（﹣2）=0，设A、B对应的参数分别为t1，t2，则|QA|•|QB|=|t1t2|=||，同理，|QC|•|QB|=||=||，∴|QA|•|QB|=|QC|•|QD|．23．已知函数，x∈R．（1）证明对∀a、b∈R，且a≠b，总有：|f（a）﹣f（b）|＜|a﹣b|；（2）设a、b、c∈R，且，证明：a+b+c≥ab+bc+ca．【考点】R4：绝对值三角不等式；R5：绝对值不等式的解法．【分析】（1）利用放缩法和绝对值三角不等式的性质即可证明，（2）由已知a+b+c=3，利用基本不等式即可证明【解答】证明：（1）若a+b=0时，不等式显然成立．（2）由已知a+b+c=3，则3（a+b+c）=（a+b+c）2=a2+b2+c2+2ab+2bc+2ca，=，≥ab+bc+ca+2ab+2bc+2ca，=3（ab+bc+ca）故a+b+c≥ab+bc+ca．2017年6月19日。

舒城中学2017届高三仿真试题(一)理科综合可能用到的相对原子质量：H-1 C-12 N-14 O-16 Cu-64 Cl-35.5Ti-48 Sr-88 Ba-137第Ⅰ卷（选择题共126分）一、选择题（本题共13小题，每题6分。

每小题只有一个正确答案）1．下列相关叙述正确的是（）A．细胞核中可进行遗传物质的复制、转录和翻译B．分泌蛋白先经过高尔基体再经过内质网分泌到细胞外C．DNA与磷脂分子中所含元素的种类相同D．不同生物膜的基本支架是相同的，膜上蛋白质的种类、数量和功能也是相同的2．下列关于物质进出细胞的叙述正确的是（）A．膜蛋白不参与物质跨膜运输的被动运输过程B．氧气浓度不会影响哺乳动物成熟红细胞对K+的主动吸收C．胞吞与胞吐只能运输大分子物质或颗粒D．Na+进出神经细胞均需要消耗A TP3．科学家用含15N的硝酸盐作为标记物浸泡蚕豆幼苗，并追踪蚕豆根尖细胞的分裂情况，得到蚕豆根尖分生区细胞连续分裂的数据如下，下列据图所作的推测正确的是（）A．在19.3～21.3 h这个时间段，根尖细胞内可发生基因重组现象B．蚕豆根尖细胞周期中染色体存在的时间比染色质存在的时间长C．在0～2 h这个时间段，蚕豆根尖细胞的DNA分子结构稳定性最低D．蚕豆根尖细胞分裂的一个细胞周期为19.3 h4．某兴趣小组用不同浓度的生长素和乙烯利分别处理刚开始发芽的南瓜芽，三天后测得的胚轴伸长量如下表所示（“-”表示未用激素处理，“+”表示用相应的激素处理且“+”越多，激素浓度越大）。

下列相关分析错误的是（）组别处理方法（生长素量）胚轴伸长量（cm）组别处理方法（乙烯利量）胚轴伸长量（cm）1 - 10 5 - 102 生长素+ 20 6 乙烯利+ 83 生长素++ 25 7 乙烯利++ 64 生长素+++ 21 8 乙烯利+++ 5A．该实验不能说明生长素的作用具有两重性B．随着乙烯利浓度的增大，对胚轴生长的抑制作用增强C．探究生长素促进胚根伸长的最适浓度时，一般需要进行预实验D．为减少实验误差，每组实验只需处理1个南瓜芽即可5．下图是人体内苯丙氨酸与酪氨酸代谢的部分途径，下列相关叙述正确的是（）A．基因①②③一般不会同时出现在人体内的同一个细胞中B．当人体衰老时，因酶②的活性降低而导致头发变白C．苯丙酮尿症的患者会因为黑色素不能合成同时患上白化病D．基因①②③的功能说明基因通过控制酶的合成从而控制生物的性状6．果蝇的眼色由两对独立遗传的基因(A、a和B、b)控制，其中B、b位于X染色体上。

2016—2017学年度第二学期第四次统考高一理数时间：120分钟 满分:150分一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.若角α是第四象限的角，则 （ ）A. sin 0α>B. cos 0α>C. tan 0α>D. sin 20α>2.设,,a b c R ∈，且a b >，则下列不等式中恒成立的是 （ ）A.ac bc >B.11a b <C.22a b >D.33a b >3.已知直线12:4230,:210l x y l x my -+=++=，且12//l l ，则实数m 值为 （ ）A ．1-B ．1C ．0D ．24.不等式220ax bx ++>的解集为11,23⎛⎫-⎪⎝⎭，则a b += （ ）A.10B.10-C.14D.14-5.若将函数2sin 2y x =的图像向左平移12π个单位长度，则平移后图象的对称轴方程为（ ） A.()26k x k Z ππ=-∈ B.()26k x k Z ππ=+∈ C.()212k x k Z ππ=-∈ D.()212k x k Z ππ=+∈ 6.在钝角△ABC中，a ＝1，b ＝2，则最大边c 的取值范围是 ( )A ．1<c <3B ．2<c <3 C.5<c <3 D ．22<c <37.已知向量,a b r r 的夹角为120°，且||=2||=3a b r r ，，则向量2+3a b r r 在向量2+a b r r 方向上的投影为（ ）A．13 B．13 C．6 D．138.在△ABC 中，已知sin A ∶sin B ∶sin C ＝m ∶(m ＋1)∶2m ，则m 的取值范围是 （ ）A ．(0，＋∞)B ．(12，＋∞) C ．(1，＋∞) D ．(2，＋∞) 9.等比数列{}n a 的前4项和为4，前12项和为28，则它的前8项和是 （ ）A ．−8B ．12C ．−8或12D ．810.已知函数()()()sin 0f x x ωϕω=+>的图象关于直线如果存在实数0x ，使得对任意的x 都有，则ω的最小值是 （ ） A ．4 B ．6 C ．8 D ．1211.已知函数()()⎪⎩⎪⎨⎧>+≤+-=01ln 022x x x x x x f ，若()f x ax ≥，则a 的取值范围是（ ）A ．(],0-∞B ．(],1-∞C ．[2,1]-D ．[2,0]-12.在ABC V中，2,2A BA B C ==,则ABC V 面积的取值范围是 （ ）A.(0,B. (0,C. (1,D. (1,二、填空题：本大题共4小题，每小题5分，共20分。

2017年高考仿真卷（一）数学试题（总分：150 时间：120分钟）一、选择题(本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一个是符合要求的，请你将符合要求的项的序号填在括号内）1.已知集合B x x x A },02|{2≤--=为自然数集，则=⋂B A （ ） A.}2,1,0,1{- B.}2,1,0{ C.}2,1{ D.}1,0{2.若复数z 满足i z i 10)3(=+，则|z|= （ ） A.10 B.10 C.3 D.93. 设命题p e x x p x⌝>+>∀，则总有1)1(,0:为 （ ） A.1)1(,0≤+>∀xe x x 总有 B.1)1(,0≤+≤∀xe x x 总有 C.1)1(,0000≤+>∃x ex x 使得 D.1)1(,0000≤+≤∃x e x x 使得4. 在△ABC 中，已知D 是AB 边上一点，AD →＝2DB →，CD →＝13CA →＋λCB →，则λ等于 （ ）A.23B.13C.－13D.－235.已知定义在R 上的函数||2)(m x x f -=-1为偶函数，记),5(log ),3(log 25.0f b f a ==),2(m f c =则c b a ,,的大小关系为 （ ） A.c b a << B.b c a << C.a b c <<D.b a c <<6．已知等比数列{}n a ，81852=⋅⋅a a a ，则数列{}n a 2log 的前9项和等于 （ ） A. -9 B. -8 C. -7 D. -107.双曲线12222=-by a x 的渐近线与圆22(2)1x y +-=相切，则双曲线离心率为 （ ）A.32 B.2 C.52D.3 8. 执行如图所示的程序框图，如果输入的S=0，则输出的S=( )A.169B.144C.121D.1009.如图，是一个几何体的三视图，其中正视图是腰长为2的等腰直角三角形， 府视图是边长为2的正方形，则此几 何体的表面积为（ ） 266 .+A 正视图 侧视图 248 .+B32246 .++C342226 .++D 俯视图10. 设非负y x ,满足约束条件⎩⎨⎧≥-≤--,0,023y x y x 若目标函数0)b 0,(a 2>>+=by ax z 的最大值为1， 则222244ba b a +的最小值为（ ） A.5 B.6 C.7 D.8 11. 将正奇数1,3,5,7，…排成五列（如下表），按此表的排列规律，2015 所在的位置是 （ ）A.第一列 12. 已知函数1||)(-=x x f ，若关于x 的方程024)()12()(2=-+-+m x f m x f 有4个不 同的实数解，则实数m 的取值范围是 （ ） A.m < --2B.m < -2.5C.m <1.5D.m >1.5二、填空题（本大题共4小题，每小题5分，共20分） 13.在83)1(xx -的二项展开式中，常数项是____________．AN1114.已知ABC ∆的内角C B A ,,所对的边分别为c b a ,,，4,1,60==︒=c b A ，则=++++CB A cb a s i n s i n s i n ____________．15.数列}{n a 满足11,2111+-==++n n n a a a a ，其前n 项积为n T ，则=2016T __________．16.已知点P(2,2),点Q 为圆C:086222=+--+y x y x ，若|OP|=|OQ|,则POM ∆的面积为____________．三、解答题（本大题共6小题，共70分。