同位角、内错角、同旁内角习题

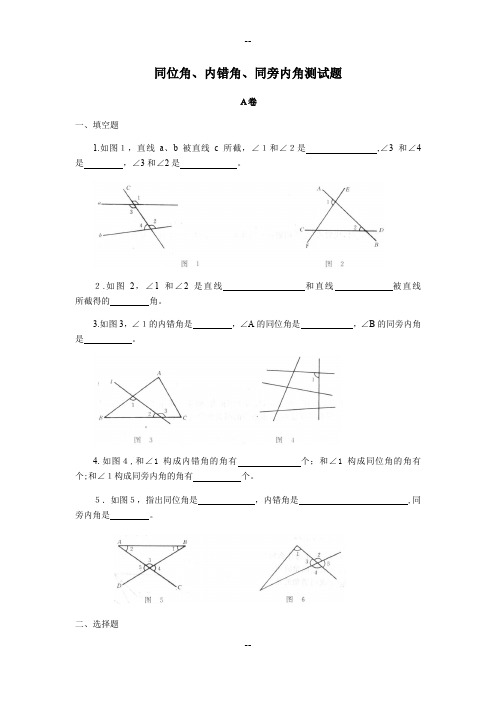
同位角、内错角、同旁内角测试题Ａ卷一、填空题1.如图１，直线a、b被直线c所截，∠１和∠２是,∠3和∠4是，∠3和∠2是。

２.如图2，∠1和∠2是直线和直线被直线所截得的角。

3.如图3，∠１的内错角是，∠A的同位角是，∠B的同旁内角是。

4.如图４,和∠1构成内错角的角有个；和∠1构成同位角的角有个;和∠１构成同旁内角的角有个。

５．如图５，指出同位角是，内错角是 ,同旁内角是。

二、选择题6.如图６,和∠1互为同位角的是( )（Ａ)∠２; （B)∠3；（C）∠4；(Ｄ)∠5。

7.如图7,已知∠1与∠２是内错角，则下列表达正确的是（ )(Ａ)由直线ＡＤ、AC被CE所截而得到的;（B）由直线ＡD、AC被BD所截而得到的；(C)由直线DＡ、DＢ被CＥ所截而得到的;(D)由直线DA、ＤＢ被AＣ所截而得到的。

8.在图８中1和２是同位角的有（)(A)（1)、(2)； (Ｂ)(2)、(3); (C）(1）、(3); （Ｄ）(2）、(4）。

９.如图9，在指明的角中，下列说法不正确的是（)(A)同位角有2对; （B)同旁内角有５对;(C)内错角有４对； (D)∠1和∠4不是内错角。

１0.如图１0,则图中共有( )对内错角(A)3; (B)４; (C)５； (Ｄ)6。

三、简答题11.如图11(1）说出∠1与∠2互为什么角？(2）写出与∠1成同位角的角；（3)写出与∠1成内错角的角。

12.如图１2(１)说出∠A与∠1互为什么角？(２) ∠B与∠2是否是同位角；(3)写出与∠2成内错角的角。

13.如图13，指出同位角、内错角、同旁内角。

B卷一、填空题1．如图1,∠１和∠2可以看作直线和直线被直线所截得的角。

2.如图2，∠1和∠2是直线和直线被直线被直线所截得的角。

３．如图3，直线DＥ、BC被直线AＣ所截得的内错角是；∠B与∠C可以看作直线、被直线所截得的角。

4.如图４,与∠EFC构成内错角的是；与∠EFC构成同旁内角的是。

七年级数学下册同位角、内错角、同旁内角练习题（含答案解析）学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，直线l 1，l 2被直线l 3所截，则（ ）A ．∠1和∠2是同位角B ．∠1和∠2是内错角C ．∠1和∠3是同位角D ．∠1和∠3是内错角2．如图，直线a 、b 被直线c 所截，则下列说法错误的是（ ）A ．1∠与2∠是邻补角B ．1∠与3∠是对顶角C ．2∠与4∠是同位角D ．3∠与4∠是内错角3．下列各图中，∠1与∠2是对顶角的是（ ）A ．B ．C ．D ．4．如图所示，下列说法错误的是（ ）A．∠1和∠3是同位角B．∠1和∠5是同位角C．∠1和∠2是同旁内角D．∠5和∠6是内错角5．给出下列说法：（1）两条直线被第三条直线所截，同位角相等；（2）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；（3）相等的两个角是对顶角；（4）从直线外一点到这条直线的垂线段，叫作这点到直线的距离．其中正确的有（）A．0个B．1个C．2个D．3个6．在下图中，1∠和2∠是同位角的是（）A．（1）、（2）B．（1）、（3）C．（2）、（3）D．（2）、（4）7．下列四幅图中，1∠和2∠是同位角的是（）A．（1）（2）B．（3）（4）C．（1）（2）（3）D．（1）（3）（4）8．如图，下列两个角是同旁内角的是（ ）A ．1∠与2∠B ．1∠与3∠C ．1∠与4∠D ．2∠与4∠9．如图所示，下列说法正确的是（ ）A ．∠2与∠1是内错角B ．∠2与∠3是同位角C ．∠3与∠B 是同旁内角D ．∠A 与∠3是内错角10．下列图形中，1∠与2∠是同位角的是（ ）A ．B ．C ．D ．11．下列所示的四个图形中，∠1和∠2是同位角的是（ ）A ．∠∠B ．∠∠∠C ．∠∠∠D ．∠∠12．下列说法正确的是（ ）A ．同位角相等B ．在同一平面内，如果a ∠b ，b ∠c ，则a ∠cC ．相等的角是对顶角D ．在同一平面内，如果a ∠b ，b ∠c ，则a ∠c二、填空题13．如图所示，（1）1∠和2∠是直线______和直线_______被第三条直线_______所截而成的_______角；（2）2∠和3∠是直线______和直线_______被第三条直线______所截而成的______角；（3）4∠和A ∠是直线______和直线______被第三条直线______所截而成的_______角．14．如图，直线,AB CD 与直线,EF GH 分别相交，图中的同旁内角共有_______对．15．如图，∠1和∠B 是直线____和直线____被直线____所截得到的_____角；∠2和∠4是直线____和直线____被直线____所截得到的_____角；∠D和∠4是直线___和直线___被直线___所截得到的_____角.16．如图，四边形ABCD是正方形，点E在BC上，∠ABE绕正方形的中心经顺时针旋转后与∠DAF重合，则∠DGE=______度．17．回顾之前所学内容填空：同位角：图中∠1与∠5，这两个角分别在直线AB，CD的同一方（上方），并且都在直线EF的同侧（右侧），具有这种位置关系的一对角叫做__________．图中还有同位角：__________．内错角：∠3与∠5，这两个角分别在直线AB，CD之间，并且分别在直线EF两侧，（∠3在直线EF左侧，∠5在直线EF右侧），具有这种位置关系的一对角叫做__________．图中还有内错角：__________．同旁内角：∠3与∠6，这两个角分别在直线AB，CD之间，但它们在直线EF的同一旁（左侧），具有这种位置关系的一对角叫做__________．图中还有同旁内角：__________．18．如图所示，1∠与2∠是________角，2∠与4∠是______角，2∠与3∠是__________角．19．空间两条不重合的直线的位置关系有________、________、________三种．三、解答题20．如图中，共有几对内错角？这几对内错角分别是哪两条直线被哪一条直线所截构成的？21．根据图形填空：（1）若直线,ED BC 被直线AB 所截，则1∠和_____是同位角；（2）若直线,ED BC 被直线AF 所截，则3∠和_____是内错角；（3）1∠和3∠是直线,AB AF 被直线______所截构成的内错角；（4）2∠和4∠是直线AB ，______被直线BC 所截构成的_____角．22．如图∠1、∠2、∠3、∠4、∠5中，哪些是同位角？哪些是内错角？哪些是同旁内角？参考答案：1．C【分析】两条直线a、b被第三条直线c所截，在截线c的同旁，被截两直线a、b的同一侧的角（都在左侧或者都在右侧），把这样的两个角称为同位角；根据定义分别判断即可．【详解】解：∠1和∠2既不是同位角，也不是内错角，故选项A、B错误；∠1和∠3是同位角，故选项C正确，选项D错误；故答案为：C．【点睛】本题考查了同位角、内错角、同旁内角，掌握同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U”形是解题的关键．2．D【分析】利用邻补角、对顶角、同位角、同旁内角定义解答即可．【详解】解：A 、1∠与2∠是邻补角，故原题说法正确；B 、1∠与3∠是对顶角，故原题说法正确；C 、2∠与4∠是同位角，故原题说法正确；D 、3∠与4∠是同旁内角，故原题说法错误；答案：D ．【点睛】此题主要考查了邻补角、对顶角、同位角、同旁内角，关键是掌握各种角的定义．3．A【分析】根据对顶角的定义，即可一一判定．【详解】解：A 、∠1与∠2是对顶角，故A 选项正确；B 、∠1与∠2不是对顶角，故B 选项错误；C 、∠1与∠2不是对顶角，故C 选项错误；D 、∠1与∠2不是对顶角，故D 选项错误．故选：A ．【点睛】本题主要考查了对顶角的定义，熟记对顶角的图形是解题的关键．4．B【分析】根据同位角、内错角、同旁内角的意义：两条直线被第三条直线所截，在截线的同旁，在被截的两直线的同一侧的角叫做同位角；两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间的两个角叫做内错角；两条直线被第三条直线所截，在截线同旁，且在被截两条直线之内的两角叫做同旁内角，可得答案．【详解】解：A 、∠1和∠3是同位角，故此选项不符合题意；B 、∠1和∠5不存在直接联系，故此选项符合题意；C 、∠1和∠2是同旁内角，故此选项不符合题意；D 、∠1和∠6是内错角，故此选项不符合题意；故选B ．【点睛】本题考查了同位角、内错角、用旁内角，利用同位角、内错角、同旁内角的意义是解题关键． 5．B【分析】正确理解对顶角、同位角、相交线、平行线、点到直线的距离的概念，逐一判断．【详解】解：（1）同位角只是一种位置关系，只有两条直线平行时，同位角相等，错误；（2）强调了在平面内，正确；（3）不符合对顶角的定义，错误；（4）直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，不是指点到直线的垂线段的本身，而是指垂线段的长度．故选：B．【点睛】本题主要考查了对顶角、同位角、相交线、平行线、点到直线的距离，正确理解相关概念是解题的关键．6．B【分析】根据同位角的特征：两条直线被第三条直线所截形成的角中，两个角都在两条被截直线的同侧，并且在第三条直线（截线）的同旁，由此判断即可．【详解】解：∠∠1和∠2是同位角；∠∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共，∠1和∠2不是同位角；∠∠1和∠2是同位角；∠∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共，∠1和∠2不是同位角．故选：B．【点睛】本题考查三线八角中的某两个角是不是同位角，同位角完全由两个角在图形中的相对位置决定．在复杂的图形中判别同位角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形．7．A【分析】互为同位角的两个角，都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做同位角．【详解】解：根据同位角的定义，图（1）、（2）中，∠1和∠2是同位角；图（3）∠1、∠2的两边都不在同一条直线上，不是同位角；图（4）∠1、∠2不在被截线同侧，不是同位角．故选：A．【点睛】本题考查同位角的概念，是需要熟记的内容．即两个都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做同位角．8．B【分析】根据同旁内角的概念求解即可．【详解】解：由图可知，∠1与∠3是同旁内角，∠1与∠2是内错角，∠4与∠2是同位角，故选：B ．【点睛】本题考查了同旁内角的概念，属于基础题，熟练掌握同位角，同旁内角，内错角的概念是解决本题的关键．9．C【分析】根据内错角、同位角、同旁内角的定义进行判断即可．【详解】∠2与∠1不是内错角，A 选项错误，不符合题意；∠2与∠3是邻补角，B 选项错误，不符合题意；∠3与∠B 是同旁内角，C 选项正确，符合题意；∠A 与∠3是同位角，D 选项错误，不符合题意；故选：C ．【点睛】本题考查了内错角、同位角、同旁内角的定义，即同位角：在截线的同旁，在被截两直线的同方向；内错角：在截线的两旁，在被截两直线的内部；同旁内角：在截线的同一侧，夹在被截两直线的之间；熟练掌握知识点是解题的关键．10．D【分析】根据同位角的定义解答．【详解】A 、B 、C 中的1∠与2∠不是同位角，D 中的1∠与2∠是同位角；故选：D ．【点睛】此题考查同位角的定义，熟记定义是解题的关键．11．C【分析】在截线的同侧，并且在被截线的同一方的两个角是同位角，所以∠∠∠符合要求．【详解】解：图∠、∠、∠中，∠1与∠2在截线的同侧，并且在被截线的同一方，是同位角；图∠中，∠1与∠2的两条边都不在同一条直线上，不是同位角．故选：C ．【点睛】此题主要考查了内错角、同位角和同旁内角的定义，解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．12．D【分析】根据同位角的定义、垂线的性质、对顶角的性质、平行公理依次判断．【详解】解：A. 同位角不一定相等，故该项不符合题意；B. 在同一平面内，如果a ∠b ，b ∠c ，则a //c ，故该项不符合题意；C. 相等的角不一定是对顶角，故该项不符合题意；D. 在同一平面内，如果a//b，b//c，则a//c，故该项符合题意；故选：D．【点睛】此题考查了语句的判断，正确掌握同位角的定义、垂线的性质、对顶角的性质、平行公理是解题的关键．13．BA CE BD同位BA CA BD同旁内BA CE AC内错【分析】根据同位角、内错角及同旁内角的定义：两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形即可得出答案．【详解】解：由图可知：（1）1∠和2∠是直线BA和直线CE被第三条直线BD所截而成的同位角；∠是直线BA和直线CA被第三条直线BD所截而成的同旁内角；（2）2∠和3（3）4∠和A∠是直线BA和直线CE被第三条直线AC所截而成的内错角，故答案为：BA；CE；BD；同位；BA；CA；BD；同旁内；BA；CE；AC；内错．【点睛】此题考查了同位角、内错角及同旁内角的知识，属于基础题，掌握定义是关键．14．16【分析】根据同旁内角的定义：两直线被第三条直线所截，在截线的同一侧，被截线的内部的两个角是同旁内角，注意每一个“三线八角”基本图形都有两对同旁内角，从对原图形进行分解入手即可求得答案．【详解】解：直线AB、CD被EF所截有2对同旁内角；直线AB、CD被GH所截有2对同旁内角；直线CD、EF被GH所截有2对同旁内角；直线CD、GH被EF所截有2对同旁内角；直线GH、EF被CD所截有2对同旁内角；直线AB、EF被GH所截有2对同旁内角；直线AB、GH被EF所截有2对同旁内角；直线EF、GH被AB所截有2对同旁内角．共有16对同旁内角．故答案为：16．【点睛】此题考查了同旁内角的知识，属于基础题，掌握定义是关键．15．（1）AD（2）BC（3）AB（4）同位（5）AB（6）CD（7）AC（8）同位（9）AC（10）AD（11）CD（12）同旁内【分析】根据两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形解答．【详解】∠1和∠B是直线AD和直线BC被直线A所截得到的同位角；∠2和∠4是直线AB和直线CD被直线AC所截得到的同位角；∠D和∠4是直线AC和直线AD被直线DC所截得到的同旁内角.【点睛】本题主要考查了三线八角的问题，熟记同位角、内错角、同旁内角的位置关系是解决此类问题的关键．16．90【分析】由旋转的性质得∠ADF=∠BAE，再根据正方形的性质，得∠DAF=90°，从而得∠AFD+∠ADF=90°，即∠AFD+∠BAE=90°，再由三角形内角和定理得出∠AGF=90°，即可由对顶角相等求得答案．【详解】解：∠△ABE绕正方形的中心经顺时针旋转后与△DAF重合，∠∠ADF=∠BAE，∠四边形ABCD是正方形，∠∠DAF=90°，∠∠AFD+∠ADF=90°，∠∠AFD+∠BAE=90°，∠∠AFD+∠BAE+∠AGF=180°，∠∠AGF=90°，∠∠DGE=∠AGF=90°，故答案为：90．【点睛】本题考查旋转的性质，三角形内角和定理，对顶角性质，熟练掌握旋转的性质是解题的关键．17．同位角∠2和∠6；∠3和∠7；∠4和∠8内错角∠4和∠6同旁内角∠4和∠5【解析】略18．同位同旁内内错【分析】根据同位角、内错角及同旁内角的定义：两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形即可得出答案．【详解】解：由图形可得，∠1与∠2是同位角；∠2与∠4是同旁内角；∠2与∠3是内错角．故答案为：同位、同旁内、内错．【点睛】此题考查了同位角、内错角及同旁内角的知识，属于基础题，掌握定义是关键．19．相交平行异面【分析】在空间，直线与直线的位置关系有平行、相交、异面三种，在同一平面内两条不重合的直线的位置关系是平行或相交，根据两条直线所在的空间解答即可.【详解】在空间，直线与直线的位置关系有相交、平行、异面，故答案为：相交、平行、异面.【点睛】此题考查相交于平行的特征及性质，关键是要明确两条直线所在的平面是在空间或是在同一平面内.20．BC、BE被DF截得的两对内错角；∠DFB和∠CDF；∠FDB和∠FDB；AC、AD被BE截得的两对内错角：∠AFE和∠CEF，∠AEF和∠EFD【分析】根据内错角的定义：两条直线被第三条直线所截形成的角中，若两个角都在两直线之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．所以由图形可得答案．【详解】∠DFB和∠CDF，∠FDB和∠FDB 是BC、BE被DF截得的内错角；∠AFE和∠CEF，∠AEF和∠EFD是AC、AD被BE截得的内错角.【点睛】本题主要考查了内错角的定义，三线八角中的某两个角是不是内错角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别内错角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．内错角的边构成“Z“形，认真识图是关键．21．（1）2∠；（3）ED；（4）AF，同位∠；（2）4【分析】（1）根据图形及同位角的概念可直接进行求解；（2）根据图形及内错角的概念可直接进行求解；（3）根据图形及内错角的概念可直接进行求解；（4）根据图形及同位角的概念可直接进行求解．【详解】解：由图可得：（1）若直线,ED BC 被直线AB 所截，则1∠和2∠是同位角；故答案为2∠；（2）若直线,ED BC 被直线AF 所截，则3∠和4∠是内错角；故答案为4∠；（3）1∠和3∠是直线,AB AF 被直线ED 所截构成的内错角；故答案为ED ；（4）2∠和4∠是直线AB ，AF 被直线BC 所截构成的同位角；故答案为AF ，同位．【点睛】本题主要考查内错角及同位角的概念，熟练掌握同位角及内错角的概念是解题的关键． 22．同位角有∠1和∠5；∠4和∠3；内错角有∠2和∠3；∠1和∠4；同旁内角有∠3和∠5；∠4和∠5；∠4和∠2．【分析】同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．依此即可得出答案．【详解】解：∠∠1和∠5在截线AC 同侧，在被截直线BE ，CE 同方向所成的角；∠4和∠3，在截线CE 的上方，被截直线DB 、EB 的左侧，∠同位角有∠1和∠5；∠4和∠3，共2对；∠∠2和∠3在截线BD 两侧，被截直线AC 与CE 内部；∠1和∠4在截线BE 两侧，被截直线AC 与CE 内部， ∠内错角有∠2和∠3；∠1和∠4,共2对；∠∠3和∠5在截线CD 同侧，被截直线CB 与DB 内部；∠4和∠5在截线CE 同侧，被截直线CB 与EB 的内部；∠4和∠2在截线BE 同侧，被截直线DB 与DE 的内部，∠同旁内角有∠3和∠5；∠4和∠5；∠4和∠2，共3对.【点睛】本题考查了同位角、内错角、同旁内角，三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．。

绝密★启用前一、单选题1．[单选题]下列图形中1∠与2∠是内错角的是A ．B ．C ．D ．答案：A 解析：A. <2与<1是内错角，故此选项正确；B. <2与<1的对顶角是内错角，故此选项错误；C. <2与<1 是同旁内角，故此选项错误；D. <2与<1的邻补角是内错角，故此选项错误；线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角.掌握内错角的定义是解答本题的关键.2．[单选题]已知如图AB 、BE 被AC 所截，下列说法不正确的是（ ）A ．1∠与2∠是同旁内角B ．1∠与ACE ∠是内错角C ．B 与ACB ∠是同位角D ．1∠与3∠不是同位角 答案：C 解析： 解析：根据同位角、内错角、同旁内角的定义可以直接得到答案. 【详解】 解：A. 1∠与2∠是同旁内角，正确但不符合题意；B. 1∠与ACE ∠是内错角，正确但不符合题意；C. B ∠与ACB ∠是同位角，错误符合题意；D.1∠与3∠不是同位角，正确但不符合题意.故选：C. 【点睛】本题主要考查了三线八角.3．[单选题]如图，∠1与∠2不能构成同位角的图形的是（ ）A ．B．C．D．答案：D解析：解析：根据同位角的定义来分析判断即可，两条直线被第三条直线所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角.【详解】由同位角的定义可知图A、B、C中的∠1和∠2可以构成同位角，D中的∠1和∠2构不成同位角.故本题答案为：D.【点睛】同位角的定义是本题的考点，根据同位角的定义正确识别同位角是解题的关键. 4．[单选题]如图，下列说法错误的是（）A．∠1与∠3是对顶角B．∠3与∠4是内错角C．∠2与∠6是同位角D．∠3与∠5是同旁内角答案：C解析：根据对顶角定义、内错角定义、同位角定义、同旁内角定义进行分析即可．【详解】A、∠1与∠3是对顶角，故A说法正确；B、∠3与∠4是内错角，故B说法正确；C、∠2与∠6不是同位角，故C说法错误；D、∠3与∠5是同旁内角，故D说法正确；故选：C．【点睛】本题考查对顶角、内错角、同位角和同旁内角的定义，掌握其定义是选择本题答案的关键．5．[单选题]下列选项中，∠ 5和∠6不是同旁内角的是（）A．B．C．D．答案：B解析：根据同旁内角的定义:两条直线被第三条直线所截，在截线同旁，且在被截线之内的两角，叫做同旁内角.进行解答【详解】A. ∠5和∠6是同旁内角,不合题意,故此选项错误.B.∠5和∠6不是同旁内角,符合题意,故此选项正确C.∠5和∠6是同旁内角,不合题意,故此选项错误D.∠5和∠6是同旁内角,不合题意,故此选项错误【点睛】本题考查同旁内角的定义,理解掌握同旁内角定义是解题关键6．[单选题]如图，直线1l和2l被直线3l所截，则（）A ．1∠和2∠是同位角B ．1∠和2∠是内错角C ．1∠和3∠是同位角D ．1∠和3∠是内错角 答案：C 解析：根据同位角和内错角的定义进行分析即可． 【详解】同位角是位于两直线及截线的同侧，内错角是位于两直线内侧及截线两侧，故1∠和3∠是同位角； 故选：C ． 【点睛】本题考查了同位角和内错角的判断，熟练掌握基本概念是解决这类问题的关键． 8．[单选题]如图，点D 、E 分别为三角形ABC 边BC 、AC 上一点，作射线DE ，则下列说法错误的是（ ）A ．∠1与∠3是对顶角B ．∠2与∠A 是同位角C ．∠2与∠C 是同旁内角D ．∠1与∠4是内错角解析：根据同位角、内错角以及同旁内角的概念进行判断．【详解】解：A、∠1与∠3是对顶角，说法正确；B、∠2与∠A是同位角，说法正确；C、∠2与∠C是同旁内角，说法正确；D、∠2与∠4是内错角，说法错误．故选：D．【点睛】考查了同位角、内错角以及同旁内角，解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．9．[单选题]如图，下列结论正确的是（）.A．∠5与∠2是对顶角；B．∠1与∠3是同位角；C．∠2与∠3是同旁内角；D．∠1与∠2是同旁内角.根据对顶角即三线八角的特征可得∠1与∠2是同旁内角，故选D。

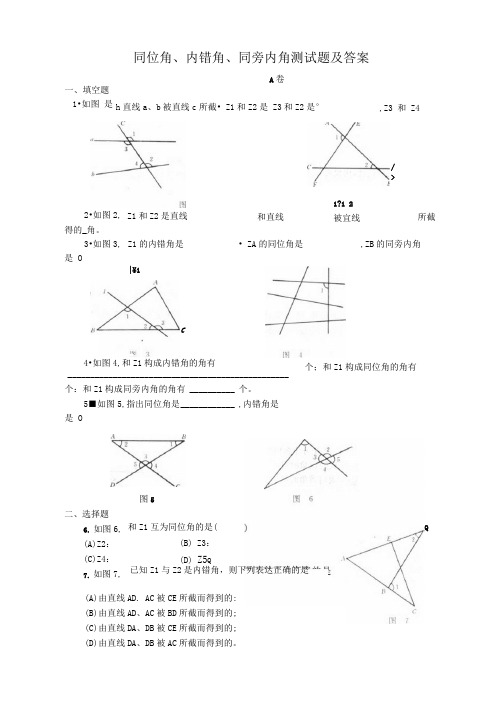
同位角、内错角、同旁内角测试题及答案A卷h直线a、b被直线c所截• Z1和Z2是 Z3和Z2是°|¥14•如图4,和Z1构成内错角的角有_________________________________________________个：和Z1构成同旁内角的角有 __________ 个。

5■如图5,指出同位角是____________ ,内错角是是 O/>1?1 2被宜线2•如图2,得的_角。

3•如图3,是 OZ1和Z2是直线Z1的内错角是和直线所截• ZA的同位角是,ZB的同旁内角图5二、选择题6.如图6,(A)Z2：(C)Z4：7.如图7,Q 和Z1互为同位角的是((B) Z3：(D) Z5Q已知Z1与Z2是内错角，则下列表达正确的是(A)由直线AD. AC被CE所截而得到的:(B)由直线AD、AC被BD所截而得到的;(C)由直线DA、DB被CE所截而得到的;(D)由直线DA、DB被AC所截而得到的。

一、填空题1•如图是,Z3 和Z4个；和Z1构成同位角的角有C8•在图8中1和2是同位角的有(RI(A)(1). (2)：9.如图9,在指明的角中，下列说法不正确的是()(A) 同位角有2对；(C)内错角有4对：(B)(2)、(3)：(D)(2)、(4)。

(B)同旁内角有5对：(D)Z1和Z4不是内错角。

(B)4：⑷3：三、简答题11.如图11(1)说出Z1与Z2互为什么角?(2)写出与Z1成同位角的角；(3)写出与Z1成内错角的角。

)对内错角(05：(D)6。

12.如图12(D说出ZA与Z1互为什么角?(2) ZB与Z2是否是同位角；⑶写出与Z2成内错角的角013.如图13.指出同位角、内错角、同旁内角.B卷一、填空题1 •如图1, Z1和Z2可以看作直线和直线被直线所截得的角。

截得的 ________ 角。

3•如图3,直线DE、BC被直线AC所截得的内错角是宜线、被直线_______ 所截得的_______ 角°图34•如图4,与ZEFC构成内错角的是________的是5.如图5,与Z1构成内错角的角有_个：与Z1构成同旁内角的角有 __________ 个。

2019年4月16日初中数学作业一.单选题1.已知Z1和Z2是同旁内角，Zl=60° , Z2等于（） A. 140°B. 120°C. 60。

D.无法确定 【答案】D【解析】【分析】 本题只是给出两个角的同旁内角关系，没有两直线平行的条件，故不能判断两个角的数 量关系.【详解】解：同旁内角只是一种位置关系，两直线平行时同旁内角互补，不平行时无法确定同旁 内角的人小关系，故选D.【点睛】特别注意，同旁内角互补的条件是两直线平行.[Wr]【分析】 本题需先根据同位角的定义进行筛选，即町得岀答案.【详解】A 、•••根据同位角的定义得:Z1与Z2不是同位角,故本选项错误：E 、I 根据同位角的定义得:Z1与Z2是同位角,故本选项正确：C. I 根据同位角的定义得:学校: _____________ 姓名： _____________ 班级:____________ 考号： _____________ 2.下列各图中，乙1与乙2是同位角的是（Z1与Z2不是同位角，故本选项错误：D 、•・•根据同位角的定义得:Z1与Z2不是同位角，故本选项错误.故选E.【点睛】本题主要考查了同位角，在解题时要根据同位角的定义进行筛选是本题的关键.【答案］C【分析】 根据同位角：两条直线彼第三条直线所截形成的角中，若两个角都在两直线的同侧，并 且在第三条直线（截线）的同旁，则这样一对角叫做同位角进行分析即可.【详解】如图①，Zls Z2是直线加与直线“被直线"所截形成的同位角，故①符合题意；如图②，ZU Z2是直线卩与直线q 被直线『所截形成的同位角，故②符合题意；如图③，Z1是直线d 与直线e 构成的夹角，Z2是直线g 与直线/形成的夹角，Z1与Z2不是同位角，故③不符合题意；如图④，ZU Z2是直线a 与直线b 被直线c 所截形成的同位角，故④符合题意.故选C.【点睛】本题考查了同位角，关键是掌握同位角的边构成“F “形，内错角的边构成“Z“形，同3.如图所示，乙1和乙2是同位角的是（D.旁内角的边构成W 形・4.下列所示的四个图形中，Z1和Z2是同位角的是（）• • •【答案】D【解析】【分析】 根据同位角，内错角，同旁内角的概念解答即可.【详解】Z1和Z2是同位角的是①©④.故选D.【点睛】本题考查了同位角，内错角，同旁内角的概念，关键是根据同位角, 【分析】 根据同位角的特征：两条直线被第三条直线所截形成的角中，两个角都在两条被截直线 的同侧，并且在第三条直线（截线）的同旁，由此判断即可.【详解】 解：A 、B. D 中Z1和Z2是同位角；C 、Z1和Z2不满足两条直线彼第三条直线所截 形成的角，所以不是同位角；故选：C.【点睛】 本题考查三线八角中的某两个角是不是同位角，同位角完全由两个角在图形中的相对位 置决定.在复杂的图形中判别同位角时，应从角的两边入于具有上述关系的角必有两 试卷第3页，总18页B.①® 内错角，同旁内角A.③©D ・④ 的概念解答.【衢］A.对顶角【答案】DB.同位角C.内错角 0.同旁内角边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即 为被截的线.同位角的边构成“F “形.6.如图，下列说法不正确的是（）两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直 线（截线）的同旁，则这样一对角叫做同位角；两条直线被第三条直线所截形成的角中， 若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁 内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第 三条直线（截线）的两旁，则这样一对角叫做内错角.【详解】A ・Z1和ZB 是DE 与被AB 所截得到的同位角，正确;B. Z1和Z4是初与AC 被DE 所截得到的内错角，正确；C. Z3和ZB 是DE 与BC 被AB 所截得到的同旁内角，正确;D. ZC 和ZA 是AB 与BC 被AC 所截得到的同旁内角，故不正确:故选D.【点睛】本题考查了同位角、内错角、同旁内角的定义，熟练掌握三种角的特征是解答本题的关 键.7.如图，直线b.c 被直线a 所截，则Z1和Z2的关系是（）【衢】【分析】A. Z1和ZB 是同位角C. Z3和ZB 是同旁内角【答案】D 【梯】【分析】B. Z1和Z4是内错角 D. ZC 和ZA 不是同旁内角结合图形，根据同位角、内错角、同旁内角的概念进行判断即可.【详解】观察图形可知，Z1和Z2两个角都在两被截直线b和c的内侧，并且在第三条直线a（截线）的同旁，故Z1和Z2是直线b、c被a所截而成的同旁内角，故选D.【点睛】本题考查了“三线八角”，熟练掌握同位角、内错角、同旁内角的图形特征是解题的关键.8.Z1与Z2是内错角，Zl=30°,则Z2的度数为（）A.30°B. 150°C. 30°或150°D.不能确定【答案】D【和】【分析】两直线平行时内错角相等，不平行时无法确定内错角的人小关系，据此分析判断即可得.【详解】内错角只是一种位置关系，并没有一定的大小关系，只有两直线平行时，内错角才相等，故选D.【点睛】本题考查了三线八角，明确同位角、内错角、同旁内角只是两个角的一种位置关系，而没有一定的大小关系是解此类问题的关键.9.两条直线被第三条直线所截，若Z1与Z2是同旁内角，且Zl=70°,则（）A.Z2=70°B. Z2=110°C. Z2=70O S EZ2=110°D. Z2的度数不能确定【答案】D【解析】【分析】两直线被第三条直线所截，只有当两条被截直线平行时，内错角相等，同位角相等，同旁内角互补.不平行时以上结论不成立.【详解】】解：因为两条直线的位置关系不明确，所以无法判断Z1和Z2大小关系.故选：D.【点睛】本题考查平行线的性质，注意性质定理的条件是两直线平行.10.如图，点O是宜线AB上一点，OE, OF分别平分ZAOC和ZBOC,当OC的位置发生变化时（不与直线AB重合），那么ZEOF的度数（）A.不变，都等于90°B.逐渐变大C.逐渐变小D.无法确定【答案】A【解析】【分析】由0E与OF为角平分线，利用角平分线定义得到两对角相等，由平角的定义及等式的性质即可求出所求角的度数.【详解】TOE、OF分别是ZAOC. ZBOC的角平分线，A ZAOE=ZCOE, ZCOF=ZBOF, V ZAOC+ ZCOB= ZAOE+ ZCOE+ ZCOF+ ZBOF=180。

《同位角、内错角、同旁内角》精品练习题一、填空题1.(1)∠1和∠2是直线_________、_________被直线_________所截得的__________角；(2)∠2和∠4是直线_________、_________被直线_________所截得的__________角；(3)∠5和∠2是直线_________、_________被直线_________所截得的__________角；(4)如图中，同位角共有____对，分别是______________________________________________.(5)如图中，内位角共有____对，分别是_____________________________.(6)如图中，同旁内角共有____对，分别是_____________________________.cab（第1题）（第2题）2.(1)∠1和∠B是直线_________、_________被直线_________所截得的__________角；(2)∠2和∠3是直线_________、_________被直线_________所截得的__________角；(3)∠2和∠B是直线_________、_________被直线_________所截得的__________角；(4)∠1和∠4是直线_________、_________被直线_________所截得的__________角.3.如图，∠1和∠6的同位角是__________，∠1和∠6的内错角是__________，∠6的同旁内角是__________.（第3题）（第4题）4. 如图，∠1和∠2是_______角，∠1和∠7_______角，∠3和∠4_______角，∠4和∠6_______角，∠5和∠7_______角.1 32 A E CDBF 5.如图，∠DAC 与∠C 是由直线_________、_________被直线__________所截得到的__________角；∠DAC 和∠B 是直线_________、_________被直线_________所截得的__________角∠B 和∠C 是直线_________、_________被直线_________所截得的__________角。

同位角、内错角、同旁内角（习题）例题示范例 1：如图，判断下列各组角的位置关系：①∠1 与∠2；②∠1 与∠7；③∠1 与∠BAD；④∠2 与∠6．思路分析操作步骤：①找角；②找角的边所在的直线；③找到截线与被截线，判断角的位置关系．分析可得，∠1 与∠2 是角；∠1 与∠7 是角；∠1 与∠BAD 是角；∠2 与∠6 是角．A 21 B3 4 5巩固练习1. 如图，直线 CD 与∠O 的两边相交．（1）∠O 和∠2 是直线 和直线 被直线 所截得到的 角；（2）∠2 和∠8 是直线 和直线 被直线 所截得到的 角； （3）∠2 和∠5 是直线 和直线被直线所截得到的 角．AC3 4 2 18 5O7 6 B DCD第 1 题图第 2 题图3. 如图所示，当时，有 AB ∥CE 成立，理由是．（只需写出一个条件即可）DE第 3 题图第 4 题图4. 如图，若∠1=∠2，则下列结论：①∠3=∠4；②AB ∥CD ；③AD ∥BC ．其中正确的是 ．（填序号）5.如图，点B 在DC 上，若BE 平分∠ABD，∠DBE=∠A，则BE AC．理由如下：E AD B∵BE 平分∠ABD （）∴∠ABE=∠DBE （角平分线的定义）∵∠DBE=∠A （）∴=∠A （）∴BE AC （）6.已知：如图，E 为DF 上的点，B 为AC 上的点，∠1=∠2，AC∥DF．求证：∠C=∠D．证明：如图，∵∠1=∠2 （）∠1=∠3 （）∴∠2=∠3 （）∴BD∥CE （）∴∠C=∠ABD （）∵AC∥DF （）∴∠D=∠ABD （）∴∠C=∠D （等量代换）思考小结1.动手操作：利用如图所示的方式，可以折出“过直线外一点和已知直线平行”的直线，依据是 ．2. 阅读材料什么是推理生活中，我们往往可以通过观察、实验来寻找规律，从而得出结论．但是要判断一个数学结论是否正确，仅仅依靠经验、观察或实验是不够的，必须一步一步、有理有据地进行推理． 推理就是由一个或几个已知的判断（前提），推导出一个未知的结论的思维过程．其作用是从已知的知识得到未知的知识， 特别是可以得到不可能通过感觉经验掌握的未知知识．几何推理是我们中学接触最多的一种推理形式．要想进行严格的几何推理，首先要有一些对应前提．这些前提我们叫做“基本事实”或“定理”，比如我们学过的“同位角相等，两直线平行”、“两点确定一条直线”等都是一些基本事实．这些作为大前提，是我们进行推理的主要依 据．而根据这些“基本事实”或“定理”，我们对某个句子进行判断或说明的过程就是证明． 例如，如下的推理： 已知：如图，∠ABC =∠1． 求证：AD ∥BC ． 证明：如图，∵∠ABC =∠1（已知）∴AD ∥BC （同位角相等，两直线平行）我们分析可知，每一个判断都有自己的条件和结论．上述推理中的条件就是∠ABC =∠1，代表着一组同位角相等，而结论就是 AD ∥BC ．由条件得到结论的过程叫做证明，而这个证明必须依据基本事实．我们把基本事实放在结论后的括号中，表明我们是以此为依据进行推理的．1 A【参考答案】例题示范同旁内，同位，同旁内，内错巩固练习1.（1）CD，OB，OA，同位；（2）O A，OB，CD，内错；（3）O A，OB，CD，同旁内．2. ①×②×③×④√3. ∠1=∠2，同位角相等，两直线平行．（答案不唯一，前后一致即可）4. ②5. ∥已知已知∠ABE，等量代换∥，内错角相等，两直线平行6. 已知对顶角相等等量代换同位角相等，两直线平行两直线平行，同位角相等已知两直线平行，内错角相等思考小结1. 同位角相等，两直线平行（或内错角相等，两直线平行，或同旁内角互补，两直线平行）。

同位角、内错角、同旁内角练习一、选择题1.如图，下列各组角中，互为内错角的是( )A. ∠1和∠2B. ∠2和∠3C. ∠1和∠3D. ∠2和∠52.如图，直线a，b被c所截，则∠1与∠2是( )A. 同位角B. 内错角C. 同旁内角D. 邻补角3.如图，直线a，b被直线c所截，则∠1与∠2的位置关系是( )A. 同位角B. 内错角C. 同旁内角D. 邻补角4.如下图，∠1和∠2为同旁内角的是( )A. B.C. D.5.如图，下列结论中错误的是( )A. ∠1与∠2是同旁内角B. ∠1与∠4是内错角C. ∠5与∠6是内错角D. ∠3与∠5是同位角6.如图，直线a，b被直线c所截，则∠1与∠2的位置关系是()A. 同位角B. 内错角C. 同旁内角D. 邻补角7.如图，在图中∠BAO和∠AOC是一对()A. 内错角B. 同旁内角C. 同位角D. 对顶角8.如图，直线l1，l2被直线13所截，则( )A. ∠1和∠2是同位角B. ∠1和∠2是内错角C. ∠1和∠3是同位角D. ∠1和∠3是内错角9.如图，∠1的内错角是( )A. ∠1B. ∠2C. ∠3D. ∠410.如图，下列说法错误的是( )A. ∠1与∠3是对顶角B. ∠3与∠4是内错角C. ∠2与∠6是同位角D. ∠3与∠5是同旁内角11.如图，直线AB，CD分别与直线EF交于点G，M，GH，MN分别与AB，CD交于点G，M，有下列结论：①∠1与∠4是同位角；②∠2与∠5是同位角；③∠EGB与∠GMD是同位角；④∠3与∠4是同旁内角．其中正确的结论有()A. 4个B. 3个C. 2个D. 1个二、填空题12.如下图，如果∠2=100°，那么∠1的同位角等于______度，∠1的内错角等于______度，∠1的同旁内角等于_____度．13.如下图，标有数字的四个角中，属于内错角的是________．14.已知直线a、b被直线c所截，则与∠1是内错角关系的是____．15.如图，∠1的同位角是，∠2的内错角，∠A的同旁内角是．16.如图所示，把一根筷子的一端放在水里，一端露出水面，筷子变弯了，它真的弯了吗？其实没有，这是光的折射现象，光从空气中射入水中，光的传播方向发生了改变．若不再添加新的标注，则图中与∠1是同旁内角的有________；与∠2是内错角的有________．三、解答题17.两条直线被第三条直线所截，∠1是∠2的同旁内角，∠2是∠3的内错角．(1)画出大致示意图；(2)若∠1=2∠2，∠2=2∠3，求∠1和∠2的度数．18.如图，∠1与∠2，∠3与∠4各是哪两条直线被哪一条直线所截而形成的什么角？19.两条直线都与第三条直线相交，∠1与∠2是内错角，∠1和∠3是同旁内角．(1)根据上述条件，画出符合题意的图形；(2)若∠1:∠2:∠3=1:2:3，求∠1，∠2，∠3的度数．答案和解析1.【答案】B【解析】解：A、∠1和∠2是对顶角，不是内错角，故本选项不符合题意；B、∠2和∠3是内错角，故本选项符合题意；C、∠1和∠3是同位角，不是内错角，故本选项不符合题意；D、∠2和∠5是同旁内角，不是内错角，故本选项不符合题意；2.【答案】B【解答】解：两条直线a、b被直线c所截形成的角中，∠1与∠2都在a、b直线的之间，并且在直线c的两旁，所以∠1与∠2是内错角．3.【答案】A【解答】解：直线a，b被直线c所截，∠1与∠2是同位角．4.【答案】C【解析】本题考查同旁内角的判定。

9.1 同位角、内错角、同旁内角1.下列图形中,1∠和2∠不是同位角的是( )2.如图,属于内错角的是( )A.∠1和∠2B.∠2和∠3 C .∠1和∠4 D.∠3和∠4 3.看图填空:(1)如图1,同位角一共有 对,分别是 ；内错角一共有 对,分别是 ； 同旁内角一共有 对,分别是 ； (2)如图2,同位角一共有 对,分别是 ；内错角一共有 对,分别是 ； 同旁内角一共有 对,分别是 .4.如图,1∠与哪个角是内错角,与哪个角是同旁内角? 2∠与哪个角是内错角,与哪个角是同旁内角(只需写一个角)?它们分别是哪两条直线被哪一条直线所截形成的?5.看图填空(1)如右图:①∠1和∠4是 角； ②∠1和∠3是 角； ③∠2和∠D 是 角； ④∠3和∠D 是 角； ⑤∠4和∠D 是 角； ⑥∠4和∠B 是 角. (2)如右图:①∠ABC 与 是同位角； ②∠ADB 与 是内错角； ③∠ABC 与 是同旁内角.6.如图所示,同位角一共有 对,分别是 ；内错角一共有 对,分别是 ； 同旁内角一共有 对,分别是 .c第2题3421A B C D12121212abc123456789AB CDE ABC DEF123412A BCD E7.如图,∠1和∠2,∠3和∠4各是哪两条直线被哪一条直线所截形成的?它们各是什么角?8.如图,用数字标注的角中,共有四对内错角,请把它们写出,并说明是哪两条直线被哪一条直线所截得的内错角.A. B. C. D.9.画图回答问题:如图,P 、Q 分别是直线EF 外两点,(1)过P 画AB ∥EF ,过Q 画CD ∥EF . (2)过点P 能画几条直线与EF 平行?为什么? (3)AB 与CD 平行吗?为什么? 解:AB 与CD 平行.理由:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.EFPQ A B 图1 图2参考答案一、课堂练习:1.下列图形中,1∠和2∠不是同位角的是( B )2.如图,属于内错角的是( D )A.∠1和∠2B.∠2和∠3 C .∠1和∠4 D.∠3和∠4 3.看图填空:(1)如图1,同位角一共有 4 对,分别是 ∠l 和∠5,∠2和∠6,∠3和∠7,∠4和∠8 ；内错角一共有 2 对,分别是 ∠3和∠6,∠4和∠5 ； 同旁内角一共有 2 对,分别是 ∠3和∠5,∠4和∠6 ； (2)如图2,同位角一共有 2 对,分别是 ∠l 和∠3,∠2和∠4 ；内错角一共有 0 对,分别是 ； 同旁内角一共有 1 对,分别是 ∠2和∠3 .4.如图,1∠与哪个角是内错角,与哪个角是同旁内角? 2∠与哪个角是内错角,与哪个角是同旁内角(只需写一个角)?它们分别是哪两条直线被哪一条直线所截形成的?解:1∠与DAB ∠是内错角,它是直线DE 、BC 被直线AB 所截形成的； 1∠与EAB ∠是同旁内角,它是直线DE 、BC 被直线AB 所截形成的；1∠与2∠是同旁内角,它是直线AB 、AC 被直线BC 所截形成的； 1∠与BAC ∠是同旁内角,它是直线BC 、AC 被直线AB 所截形成的； 2∠与EAC ∠是内错角,它是直线DE 、BC 被直线AC 所截形成的； 2∠与BAC ∠是同旁内角,它是直线AB 、BC 被直线AC 所截形成的.c第2题3421A B C D1212121212A BCD(2∠与DAC ∠是同旁内角,它是直线DE 、BC 被直线AC 所截形成的.)二、课后作业: 5.看图填空 (1)如右图:①∠1和∠4是 邻补 角； ②∠1和∠3是 对顶 角； ③∠2和∠D 是 内错 角； ④∠3和∠D 是 同旁内 角； ⑤∠4和∠D 是 同位 角； ⑥∠4和∠B 是 同位 角. (2)如右图:①∠ABC 与 ∠EAD 是同位角；②∠ADB 与 ∠DBC 、 ∠EAD 是内错角； ③∠ABC 与 ∠DAB 、 ∠BCD 是同旁内角. 6.如图所示,同位角一共有 6 对,分别是 ∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8,∠7和∠9,∠4和∠9 ； 内错角一共有 4 对,分别是 ∠1和∠7, ∠4和∠6, ∠5和∠9, ∠2和∠9 ；同旁内角一共有 4 对,分别是 ∠1和∠6, ∠1和∠9, ∠4和∠7, ∠6和∠9 .7.如图,∠1和∠2,∠3和∠4各是哪两条直线被哪一条直线所截形成的?它们各是什么角? 解:如图1中,∠1和∠2是直线AB 、CD 被直线BD 所截,它们是内错角；∠3和∠4是直线AD 、CB 被直线BD 所截, 它们也是内错角. 如图2中,∠1和∠2是直线AB 、CD 被直线BC 所截,它们是同旁内角； ∠3和∠4是直线AD 、CB 被直线AB 所截,它们是同位角.8.如图,用数字标注的角中,共有四对内错角,请把它们一一写出,并说明是哪两条直线被哪一条直线所截得的内错角.abc123456789AB CDEAB C DEF1234AB 图1 图2解:∠1和∠5是内错角,它们是由直线AD 、BC 被直线AC 所截形成的； ∠2和∠6是内错角,它们是由直线AB 、CD 被直线AC 所截形成的； ∠3和∠7是内错角,它们是由直线AB 、CD 被直线BD 所截形成的； ∠4和∠8是内错角,它们是由直线AD 、BC 被直线BD 所截形成的.三、新课预习: 9.画图回答问题:如图,P 、Q 分别是直线EF 外两点, (1)过P 画AB ∥EF ,过Q 画CD ∥EF .(2)过点P 能画几条直线与EF 平行?为什么?解:过点P 只能画一条直线与EF 平行.理由:经过直线外一点,有且只有一条直线与这条直线平行.(3)AB 与CD 平行吗?为什么? 解:AB 与CD 平行.理由:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.A B C DEFPQ。