同位角内错角同旁内角练习题及答案

同位角.内错角.同旁内角专项练习50题知识点:1、两条直线被第三条直线所截形成八个角，它们构成了同位角、内错角与同旁内角。

如图，直线“上被直线/所截①Z1与Z5在截线/的同侧，同在被截直线（"的上方,叫做同位角（位置相同）②Z5与Z3在截线/的两旁（交错），在被截直线4b之间（内），叫做内错角（位置在内且交错）③Z5与Z4在截线/的同侧，在被截直线之间（内），叫做同旁内角“④三线八角也可以成模型中看出。

同位角是"A”型；内错角是“Z”型：同旁内角是“U”型。

2、如何判别三线八角判别同位角.内错角或同旁内角的关键是找到构成这两个角的“三线S有时需要将有关的部分“抽出”或把无关的线略去不看，有时又需要把图形补全。

例如：A 1如图,判断下列各对角的位置关系:（DZ1与Z2：（2）Z1与Z7：（30 与ZBAD：（4）Z2与Z6：（5）/5与Z8。

我们将各对角从图形中抽岀来（或者说略去与有关角无关的线），得到下列各图。

如图所示，不难看出Z1与Z2是同旁内角：Z1与Z7是同位角：Z1与ZBAD是同旁内角；Z2与Z6是内错角：Z5与Z8对顶角。

专项练习:所截得的 角,AC 、BC 被AB 所截得的同旁内角是8、 如图2・45, AB. DC 被BD 所截得的内错角是 _________ 是 ____________ ，AD 、BC 被BD 所截得的内错角是 Z • AB 、______ 所角。

12、如图2-49,已知Z1的同旁内角等于57° 28’，求Z1的内错的度数.13、如图1, Z1和Z2可以看作直线 _________ 和直线 _________ 被直线 _______ 所截得的角。

15、如图3,直线DE 、BC 被直线AC 所截得的内错角是 ______ : ZB 与ZC 可以看作直线 __________ 、 __________ 被E ）是内错角 个 10.如图 2-47,( 11、如图2-48,图中的同位角的对数是（ )14、如图2, Z1和Z2是直线 和直线 被直线直线 ________ 所截得的________ 角o图316、如图4.与ZEFC构成内错角的是.2 1、如下图6,和Z1互为同位角的是(图I______________ :与ZEFC构成同旁内角的____ 个；与Z2构成同位角的角有 _______ 个:个。

∴∠ABE=∠DBE（角平分线的定义）
∵∠DBE=∠A（______________________________）
∴_______=∠A（______________________________）
∴BE_____AC（______________________________）
6.已知：如图，E为DF上的点，B为AC上的点，∠1=∠2，AC∥DF．
推理就是由一个或几个已知的判断（前提），推导出一个未知的结论的思维过程．其作用是从已知的知识得到未知的知识，特别是可以得到不可能通过感觉经验掌握的未知知识．几何推理是我们中学接触最多的一种推理形式．
要想进行严格的几何推理，首先要有一些对应前提．这些前提我们叫做“基本事实”或“定理”，比如我们学过的“同位角相等，两直线平行”、“两点确定一条直线”等都是一些基本事实．这些作为大前提，是我们进行推理的主要依据．而根据这些“基本事实”或“定理”，我们对某个句子进行判断或说明的过程就是证明．
例如，如下的推理：
已知：如图，∠ABC=∠1．
求证：AD∥BC．
证明：如图，
∵∠ABC=∠1（已知）
∴AD∥BC（同位角相等，两直线平行）
我们分析可知，每一个判断都有自己的条件和结论．上述推理中的条件就是∠ABC=∠1，代表着一组同位角相等，而结论就是AD∥BC．由条件得到结论的过程叫做证明，而这个证明必须依据基本事实．我们把基本事实放在结论后的括号中，表明我们是以此为依据进行推理的．
6.已知
对顶角相等
等量代换
同位角相等，两直线平行
两直线平行，同位角相等
已知
两直线平行，内错角相等
思考小结
1.同位角相等，两直线平行（或内错角相等，两直线平行，或同旁内角互补，两直线平行）

可编辑修改精选全文完整版5.1.3 同位角、内错角、同旁内角学校：__________ 姓名：__________ 班级：__________ 考号：__________一、单选题1．如图，下列各语句中，错误的语句是（ ）A ．∠ADE 与∠B 是同位角B ．∠BDE 与∠C 是同旁内角 C ．∠BDE 与∠AED 是内错角 D ．∠BDE 与∠DEC 是同旁内角2．下列各图中，∠1与∠2是内错角的是（ ）A ．B ．C ．D ．3．如图所示，下列结论中不正确的是( )A ．1∠和2∠是同位角B ．2∠和3∠是同旁内角C ．1∠和4∠是同位角D ．2∠和4∠是内错角4．如图，下列各组角是内错角( )A ．∠1和∠2B ．∠3和∠4C ．∠2和∠3D ．∠1和∠45．如图所示，下列说法错误的是( )A．∠C与∠1是内错角B．∠2与∠3是内错角C．∠A与∠B是同旁内角D．∠A与∠3是同位角6．由图可知，∠1和∠2是一对（）A．对顶角B．同位角C．内错角D．同旁内角7．如图，下列6种说法：①∠1与∠4是内错角；②∠1与∠2是同位角；③∠2与∠4是内错角；④∠4与∠5是同旁内角；⑤∠2与∠4是同位角；⑥∠2与∠5是内错角．其中正确的有 ( )A．1个B．2个C．3个D．4个二、填空题1．如图，按角的位置关系填空：∠A与∠1是______；∠A与∠3是______；∠2与∠3是______.2．如图，∠3和∠9是直线________、_______被直线_______所截而成的______角；∠6和∠9是直线_____、______被直线________所截而成的_______角.3．如图，∠1的同旁内角是____________，∠2的内错角是____________．三、解答题1．如图，直线a、b被直线l所截，已知∠1=40°，试求∠2的同位角及同旁内角的度数．参考答案一、单选题1．B解析：A、由同位角的概念可知，∠ADE与∠B是同位角，不符合题意；B、由同位角同旁内角的概念可知，∠BDE与∠C不是同旁内角，符合题意；C、由内错角的概念可知，∠BDE与∠AED是内错角，不符合题意；D、由同旁内角的概念可知，∠BDE与∠DEC是同旁内角，不符合题意．2．A解析：根据内错角的定义可知，内错角是成“Z”字形的两个角，据此逐项分析可得答案. 详解：A. ∠1与∠2是内错角,正确.B. ∠1与∠2不是内错角,故错误.C. ∠1与∠2不是内错角,故错误.D. ∠1与∠2是同旁内角,故错误.故选：A.点睛：本题考查了内错角的判断，熟记内错角的定义是解题的关键；两条直线被第三条直线所截形成的八个角中，两个角分别在截线的两侧，且在两条直线之间，具有这样位置关系的一对角叫做内错角；3．A解析：根据同位角，内错角，同旁内角以及对顶角的定义进行解答．详解：A、∠1和∠2是同旁内角，故本选项错误，符合题意；B、∠2和∠3是同旁内角，故本选项正确，不符合题意；C、∠1和∠4是同位角，故本选项正确，不符合题意；D、∠2和∠4是内错角，故本选项正确，不符合题意；故选A．点睛：考查了同位角，内错角，同旁内角以及对顶角的定义．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．4．B解析：A、∠1和∠2不是内错角，故本选项错误；B、∠3和∠4是内错角，故本选项正确；C、∠2和∠3不是内错角，故本选项错误；D、∠1和∠4不是内错角，故本选项错误，故选B．点睛：本题考查了内错角，熟知内错角的定义以及位置特征是解题的关键.5．B解析：根据同位角，同旁内角，内错角的定义可以得到A、C、D是正确的，∠2与∠3是邻补角，不是内错角．详解：A、∠C与∠1是内错角，故本选项正确；B、∠2与∠3是邻补角，故本选项错误；C、∠A与∠B是同旁内角，故本选项正确；D、∠A与∠3是同位角，故本选项正确．故选：B．点睛：本题主要考查了同位角，内错角，同旁内角的概念，比较简单．6．C解析：试题∠1与∠2是两直线被一条直线所截得到的两角，这两角分别位于截线的两侧，并且位于被截直线之间，因而是内错角．故选C.7．C解析：试题根据同位角，内错角，同旁内角的定义可知①∠1与∠4是内错角；错误，②∠1与∠2是同位角；正确，③∠2与∠4是内错角；错误, ④∠4与∠5是同旁内角；正确，⑤∠2与∠4是同位角；错误，⑥∠2与∠5是内错角．正确.有3个正确.故选C.点睛：同位角：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角；内错角：两个角在截线的两旁，又分别处在被截的两条直线异侧的位置的角；同旁内角：两个角都在截线的同旁，又分别处在被截的两条直线异侧的位置的角；二、填空题1．同旁内角同位角内错角解析：根据两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形找出即可．详解：解：根据图形，∠A与∠1是直线AC、MN被直线AB所截形成的同旁内角，∠A与∠3是直线AC、MN被直线AB所截形成的同位角，∠2与∠3是直线AC、AB被直线MN所截形成的内错角．故应填：同旁内角，同位角，内错角．点睛：本题考查了三线八角中的同旁内角，同位角，内错角的概念，知同位角、内错角、同旁内角是两直线被第三条直线所截而成的角．2．AD BD AC 同位 AC BC BD 同位角解析：根据两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形解答即可．详解：如图，∠3和∠9是直线AD、BD被直线AC所截而成的同位角；∠6和∠9是直线BC、AC被直线BD所截而成的同位角．故答案为AD、BD、AC、同位；BC、AC、BD、同位．点睛：本题考查了同位角、内错角、同旁内角，属于三线八角的问题，熟记同位角、内错角、同旁内角的位置关系是解决此类问题的关键．3．∠3，∠B；∠3解析：由内错角和同旁内角的定义可知：∠1与∠3，∠B是同旁内角；∠2的内错角是∠3.故答案为∠3，∠B；∠3.三、解答题1．∠2的同位角是140°，∠2的同旁内角是40°．解析：试题分析：首先要确定∠2的同位角、同旁内角是哪一个：因l为截线，这两个角与∠2必然位于l的同旁，即直线l的右边的∠3与∠4；再根据对顶角性质及补角定理，就可求出两角大小.解：如图，∵∠1=40°，∴∠4=∠1=40°，∠3=180°﹣∠1=140°，即∠2的同位角是140°，∠2的同旁内角是40°．。

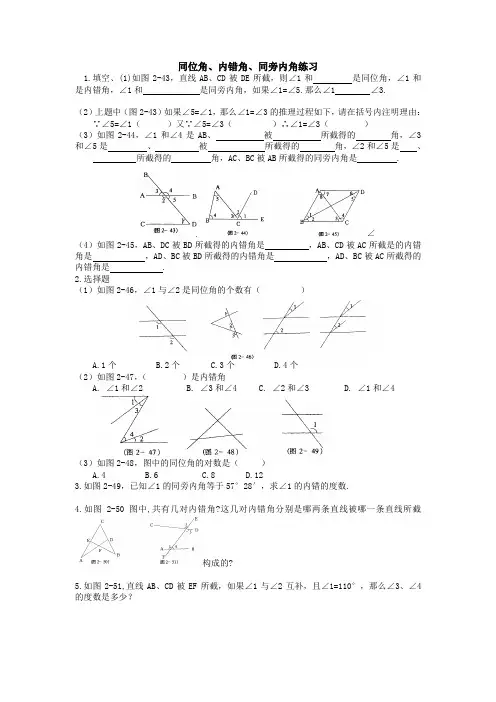
同位角、内错角、同旁内角练习1.填空、(1)如图2-43，直线AB、CD被DE所截，则∠1和是同位角，∠1和是内错角，∠1和是同旁内角，如果∠1=∠5.那么∠1 ∠3.（2）上题中（图2-43）如果∠5=∠1，那么∠1=∠3的推理过程如下，请在括号内注明理由：∵∠5=∠1（）又∵∠5=∠3（）∴∠1=∠3（）（3）如图2-44，∠1和∠4是AB、被所截得的角，∠3和∠5是、被所截得的角，∠2和∠5是、所截得的角，AC、BC被AB所截得的同旁内角是 .∠（4）如图2-45，AB、DC被BD所截得的内错角是，AB、CD被AC所截是的内错角是，AD、BC被BD所截得的内错角是，AD、BC被AC所截得的内错角是 .2.选择题（1）如图2-46，∠1与∠2是同位角的个数有（）A.1个B.2个C.3个D.4个（2）如图2-47，（）是内错角A. ∠1和∠2B. ∠3和∠4C. ∠2和∠3D. ∠1和∠4（3）如图2-48，图中的同位角的对数是（）A.4B.6C.8D.123.如图2-49，已知∠1的同旁内角等于57°28′，求∠1的内错的度数.4.如图2-50图中,共有几对内错角?这几对内错角分别是哪两条直线被哪一条直线所截构成的?5.如图2-51,直线AB、CD被EF所截，如果∠1与∠2互补，且∠1=110°，那么∠3、∠4的度数是多少？1、如图，∠1的内错角是，它们是直线、被直线所截得的；∠1的同位角是，它们是直线、被直线所截得的；∠1的同旁内角是，它们是直线、被直线所截的；2．如图，下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其中正确的是…………………………………（）（A）①、②、③（B）①、②、④（C）②、③、④（D）①、②、③、④3、如图，图中的同位角共有……………………………………………………………（）（A）6对（B）8对（C）10对（D）12对4．下面四个图形中，∠1与∠2是对顶角的图形的个数是（）A．0 B．1 C．2 D．3121212125．三条直线两两相交于同一点时，对顶角有m对，交于不同三点时，对顶角有n对，则m与n的关系是（）A．m = n B．m＞n C．m＜n D．m + n = 10 6．如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD = 38°，则∠AOC = ，∠COB = 。

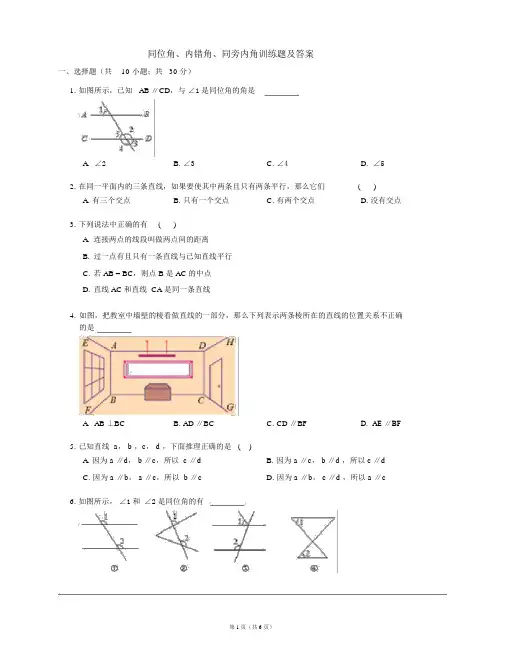
同位角、内错角、同旁内角训练题及答案一、选择题（共10 小题；共30 分）1.如图所示，已知 AB ∥CD，与∠1是同位角的角是A. ∠2B. ∠3C. ∠4D. ∠52. 在同一平面内的三条直线，如果要使其中两条且只有两条平行，那么它们()A. 有三个交点B. 只有一个交点C. 有两个交点D. 没有交点3. 下列说法中正确的有()A.连接两点的线段叫做两点间的距离B.过一点有且只有一条直线与已知直线平行C.若 AB = BC，则点 B 是 AC 的中点D.直线 AC 和直线 CA 是同一条直线4.如图，把教室中墙壁的棱看做直线的一部分，那么下列表示两条棱所在的直线的位置关系不正确的是A. AB ⊥BCB. AD ∥BCC. CD ∥BFD. AE ∥BF5.已知直线 a， b ，c， d ，下面推理正确的是 ( )A. 因为 a ∥d， b ∥c，所以 c ∥dB. 因为 a ∥c， b ∥d ，所以 c ∥dC. 因为 a ∥b， a ∥c，所以 b ∥cD. 因为 a ∥b， c ∥d ，所以 a ∥c6. 如图所示，∠1和∠2是同位角的有A. ①②B. ①③C. ①④D. ②③7.如图，下列判断不正确的是A. ∠B与∠A是同旁内角B. ∠C与∠1是内错角C. ∠2与∠3是内错角D. ∠B与∠1是同位角8.在同一平面内，下列说法正确的是( )A. 不相交的两条直线是平行线B. 不相交的两条射线是平行线C. 不相交的两条线段是平行线D. 不平行的两条线段一定相交9.三条直线 a， b ，c，若 a ∥c， b ∥c，则 a 与 b 的位置关系是 ( )A. a ⊥bB. a ∥bC. a ⊥b 或 a ∥bD. 无法确定10. 下列结论中，不正确的是 ()A.两点确定一条直线B.等角的余角相等C.过一点有且只有一条直线与已知直线平行D.两点之间的所有连线中，线段最短二、填空题（共 6 小题；共 18 分）11.在同一平面内，两条直线的位置关系只有和两种．12.平行公理的推论是：如果两条直线都与，那么这两条直线也．即三条直线 a， b ，c，如果 a ∥b ， b ∥c，那么．13.若 AB ∥CD， AB ∥EF，则∥，理由是．14.下图有对内错角．15.已知平面内四条直线共有三个交点，则这四条直线中最多有条平行线．16.如图，平行直线 AB 、 CD 与相交直线 EF 、 GH 相交，图中的同旁内角共有对．三、解答题（共 6 小题；共52 分）17.如图所示， a ∥b ，b ∥c， d 与 a 相交于点 M．(1)试判断直线 a，c 的位置关系，并说明理由；(2)判断 c 与 d ， b 与 d 的位置关系，并说明理由．18.工人师傅在铺设电缆时，为了检验三条电缆线是否平行，只检查了其中两条电缆线是否与第三条电缆线平行，你认为这种做法正确吗？请作出合理解释．19.如图，指出下列各组角是由哪两条直线被哪一条直线所截得的，并说出它们是什么角？∠1和∠2，∠2和∠6，∠4和∠7，∠3和∠5．20. 如图，直线DE，BC 被直线 AB 所截．(1)∠1与∠2，∠1与∠3，∠1与∠4各是什么角？(2)如果∠1= ∠4，那么∠1和∠2相等吗？∠1和∠3呢？为什么？21. 在同一平面内有n 条直线，当 n = 1 时，如图（ 1），一条直线将一个平面分成两个部分；当 n = 2时，如图（ 2），两条直线将一个平面最多分成四个部分．(1)在作图区分别画出当 n = 3 时，三条直线将一个平面分成最少部分和最多部分的情况；(2)当 n = 4 时，请写出四条直线将一个平面分成最少部分的个数和最多部分的个数；(3) 若 n 条直线将一个平面最多分成a n个部分， ( n + 1) 条直线将一个平面最多分成a n+1个部分，请写出 a n， a n+1， n 之间的关系式．22. 我们知道相交的两直线的交点个数是 1 ，记两平行直线的交点个数是0；这样平面内的三条平行线它们的交点个数就是0 ，经过同一点的三直线它们的交点个数就是 1 ；依次类推? ．(1)请你画图说明同一平面内的五条直线最多有几个交点？(2)平面内的五条直线可以有 4 个交点吗？如果有，请你画出符合条件的所有图形；如果没有，请说明理由．(3)在平面内画出 10 条直线，使交点个数恰好是31．答案第一部分1.D2.C3.D4.C5. C6.A7.B8.A9.B10. [2]第二部分11.相交；平行12.第三条直线平行；互相平行； a ∥c13.CD； EF；如果两条直线都与第三条直线平行，那么这两条直线也互相平行14.2415. 316.16第三部分17.(1) 因为 a ∥b ， b ∥c，所以 a ∥c．理由：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．17.(2) 因为 d ， a 都过 M 点且 a ∥c，所以 d 与 c 相交；同理： b 与 d 相交．理由：经过直线外一点，有且只有一条直线与这条直线平行．18.(1) 正确．如果两条直线都与第三条直线平行，那么这两条直线也互相平行．19. (1)∠1和∠2是同位角，是直线 BD， DE 被 AB 所截得到的；∠2和∠6是内错角，是直线AB， CD 被 BD 所截得到的；∠4和∠7是同旁内角，是直线AB， BC 被 CE 所截得到的；∠3和∠5是同旁内角，是直线DE， DC 被 CE 所截得到的．20.(1) ∠1与∠2是内错角，∠1与∠3是同旁内角，∠1与∠4是同位角．20.(2) 如果∠1= ∠4，那么∠1和∠2相等，∠1和∠3互补．理由是：因为∠1= ∠4，又根据对顶角相等知∠2= ∠4，所以∠1= ∠2．因为∠3和∠4互为补角，°所以∠3+ ∠4= 180 ，°所以∠1+ ∠3= 180 ，即∠1和∠3互补．21. (1)21.(2) 最少 5 部分，最多 11 部分．21.(3) a n+1 - a n = n + 122.(1) 如图，最多有 10 个交点．22.(2) 可以有 4 个交点，有 3 种不同的情形，如图．22. (3) 在平面内画出10 条直线，使交点个数恰好是31 ，如图。

同位角、内错角、同旁内角测试题A卷一、填空题1.如图1，直线a、b被直线c所截，∠1和∠2是，∠3和∠4是，∠3和∠2是。

直线和线∠，2.如图2∠1和2是直角。

所截得的被直线的同位角A ，∠33.如图，∠1的内错角是。

，∠B的同旁内角是是1个；和∠1如图4，和∠构成内错角的角有 4.构成同旁内角的角有个；和∠构成同位角的角有 1个。

．位角是，内错角同55.如图，指出是，同旁内角是。

二、选择题6.如图6，和∠1互为同位角的是( )(A)∠2； (B)∠3；(C)∠4； (D)∠5。

7.如图7，已知∠1与∠2是内错角，则下列表达正确的是( )(A)由直线、被所截而得到的；(B)由直线、被所截而得到的；(C)由直线、被所截而得到的；(D)由直线、被所截而得到的。

( )是同位角的有2和1中8在图8.；、(3) (B)(2)、(3)； (C)(1)(A)(1)、(2)；(4)。

(D)(2)、，在指明的角中，下列说法不正确的是( )9.如图9 对；同旁内角有对； (B)5(A)同位角有2不是内错41和∠ (D)(C)内错角有4对；∠角。

对内错角如图10，则图中共有( )10. (D)6。

(C)5(A)3； (B)4；；三、简答题 11.如图11 互为什么角？2与∠1说出∠(1)．(2)写出与∠1成同位角的角；成内错角的角。

写出与∠1(3)1212.如图 A(1)说出∠与∠1互为什么角？∠B是否是同位角；与∠2(2)成内错角的角。

写出与∠2(3)，指出同位角、内错角、同旁内角。

13.如图13B卷一、填空题被和直线可以看作直线2和∠1∠，1如图1. 直线所截得的角。

被直线和直线 1和∠2是直线 22.如图，∠所截得的角。

被直线与；∠B如图3，直线、被直线所截得的内错角是 3.所截、被直线可以看作直线∠C角。

得的；与 4.如图4，与∠构成内错角的是∠构成同旁内角的是。

1个；与∠1如图5，与∠构成内错角的角有 5.构成同旁内角的角有个；与∠构成同位角的角有 1个。

认识同位角、内错角、同旁内角（人教版）一、单选题(共10道，每道10分)1.如图，∠1和∠2是直线_____和直线_____被直线_____所截得到的_____．( )A.c，d，a，内错角B.a，d，c，内错角C.c，d，a，同位角D.c，d，a，同旁内角答案：A解题思路：∠1与直线a和c有关，∠2与直线a和d有关，所以直线a是截线，由图中的位置关系可知∠1和∠2是直线c和直线d被直线a所截得到的内错角．故选A．试题难度：三颗星知识点：同位角、内错角、同旁内角2.如图，∠1和∠2是直线_____和直线_____被直线_____所截得到的_____．( )A.b，c，a，同位角B.a，b，c，内错角C.a，c，b，同位角D.b，c，a，同旁内角答案：A解题思路：∠1与直线a和b有关，∠2与直线a和c有关，所以直线a是截线，由图中的位置关系可知∠1和∠2是直线b和直线c被直线a所截得到的同位角．故选A．试题难度：三颗星知识点：同位角、内错角、同旁内角3.如图，∠1和∠2是直线_____和直线_____被直线_____所截得到的_____．( )A.AB，BC，AC，内错角B.AB，BC，AC，同旁内角C.EF，BC，AC，同旁内角D.AB，BC，AC，同位角答案：B解题思路：∠1与直线BC和直线AC相关，∠2与直线AB和直线AC相关，所以直线AC是截线．并且∠1和∠2都位于直线AB，直线BC之间，直线AC的同侧，因此∠1和∠2是直线AB和直线BC被直线AC所截得到的同旁内角．故选B．试题难度：三颗星知识点：同位角、内错角、同旁内角4.如图，∠1和∠2是直线_____和直线_____被直线_____所截得到的_____．( )A.AC，BE，AB，内错角B.AC，BD，AB，同位角C.AC，BD，AB，同旁内角D.AC，BE，AB，同位角答案：D解题思路：∠1与直线BE和直线AB相关，∠2与直线AB和直线AC相关，所以直线AB是截线．并且∠1和∠2都位于直线AC，直线BE的右边，直线AB的同侧，因此∠1和∠2是直线BE和直线AC被直线AB所截得到的同位角．故选D．试题难度：三颗星知识点：同位角、内错角、同旁内角5.如图，与∠A是同位角的是( )A.∠1B.∠2C.∠3D.∠4答案：C解题思路：根据同位角的定义，可知图中∠3与∠A是同位角．故选C．试题难度：三颗星知识点：同位角、内错角、同旁内角6.下列四幅图中，∠1和∠2是同位角的是( )A.（1）（2）B.（3）（4）C.（1）（2）（3）D.（2）（3）（4）答案：C解题思路：根据同位角的定义，图（1）（2）（3）中，∠1与∠2是同位角，（4）中∠1与∠2不是同位角．故选C．试题难度：三颗星知识点：同位角、内错角、同旁内角7.如图，下列各组角中，不是同旁内角的是( )A.∠1与∠3B.∠5与∠6C.∠1与∠6D.∠2与∠7答案：C解题思路：∠1与∠3是直线a和直线b被直线c所截得到的同旁内角；∠5与∠6是直线b和直线c被直线a所截得到的同旁内角；∠1与∠6是直线a和直线c被直线b所截得到的同位角；∠2与∠7是直线a和直线c被直线b所截得到的同旁内角．故选C．试题难度：三颗星知识点：同位角、内错角、同旁内角8.如图，下列说法错误的是( )A.∠1与∠5是内错角B.∠4与∠5是内错角C.∠O与∠1是同旁内角D.∠3与∠5是同位角答案：B解题思路：∠1与∠5是直线OA和直线OB被直线CD所截得到的内错角，选项A说法正确；∠O与∠1是直线CD和直线OB被直线OA所截得到的同旁内角，选项C说法正确；∠3与∠5是直线OA和直线OB被直线CD所截得到的同位角，选项D说法正确；而∠4与∠5不是同位角、内错角，也不是同旁内角，因此选项B说法错误．故选B．试题难度：三颗星知识点：同位角、内错角、同旁内角9.下图中，∠1与∠2是内错角的是( )A. B.C. D.答案：D解题思路：选项A，B，C中，∠1与∠2与四条直线相关，不是同位角、内错角和同旁内角中的任何一个，选项D中，∠1与∠2是内错角．故选D．试题难度：三颗星知识点：同位角、内错角、同旁内角10.如图，下列说法正确的是( )A.∠2与∠5是同旁内角B.∠D与∠4是同位角C.∠1与∠3是内错角D.∠B与∠4是同位角答案：C解题思路：∠2与∠5，∠D与∠4不是两条直线被第三条直线所截得到的，不可能是同位角、内错角或同旁内角，所以选项A和B说法错误；∠1与∠3是直线AB和直线CD被直线AC所截得到的内错角，所以选项C说法正确；∠B与∠4是直线AB和直线AC被直线BC所截得到的同旁内角，因此选项D说法错误．故选C．试题难度：三颗星知识点：同位角、内错角、同旁内角。

同位角、内错角、同旁内角练习1.填空、(1)如图2-43，直线AB、CD被DE所截，则∠1和是同位角，∠1和是内错角，∠1和是同旁内角，如果∠1=∠5.那么∠1 ∠3.（2）上题中（图2-43）如果∠5=∠1，那么∠1=∠3的推理过程如下，请在括号内注明理由：∵∠5=∠1（）又∵∠5=∠3（）∴∠1=∠3（）（3）如图2-44，∠1和∠4是AB、被所截得的角，∠3和∠5是、被所截得的角，∠2和∠5是、所截得的角，AC、BC被AB所截得的同旁内角是.∠（4）如图2-45，AB、DC被BD所截得的内错角是，AB、CD被AC所截是的内错角是，AD、BC被BD所截得的内错角是，AD、BC被AC所截得的内错角是.2.选择题（1）如图2-46，∠1与∠2是同位角的个数有（）个个个个（2）如图2-47，（）是内错角A. ∠1和∠2B. ∠3和∠4C. ∠2和∠3D. ∠1和∠4（3）如图2-48，图中的同位角的对数是（）.6 C3.如图2-49，已知∠1的同旁内角等于57°28′，求∠1的内错的度数.4.如图2-50图中,共有几对内错角这几对内错角分别是哪两条直线被哪一条直线所截构成的5.如图2-51,直线AB、CD被EF所截，如果∠1与∠2互补，且∠1=110°，那么∠3、∠4的度数是多少1、如图，∠1的内错角是，它们是直线、被直线所截得的；∠1的同位角是，它们是直线、被直线所截得的；∠1的同旁内角是，它们是直线、被直线所截的；2．如图，下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其中正确的是…………………………………（）（A）①、②、③（B）①、②、④（C）②、③、④（D）①、②、③、④3、如图，图中的同位角共有……………………………………………………………（）（A）6对（B）8对（C）10对（D）12对4．下面四个图形中，∠1与∠2是对顶角的图形的个数是（）A．0 B．1 C．2 D．3121212125．三条直线两两相交于同一点时，对顶角有m对，交于不同三点时，对顶角有n对，则m 与n的关系是（）A．m = n B．m＞n C．m＜n D．m + n = 106．如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD = 38°，则∠AOC = ，∠COB = 。

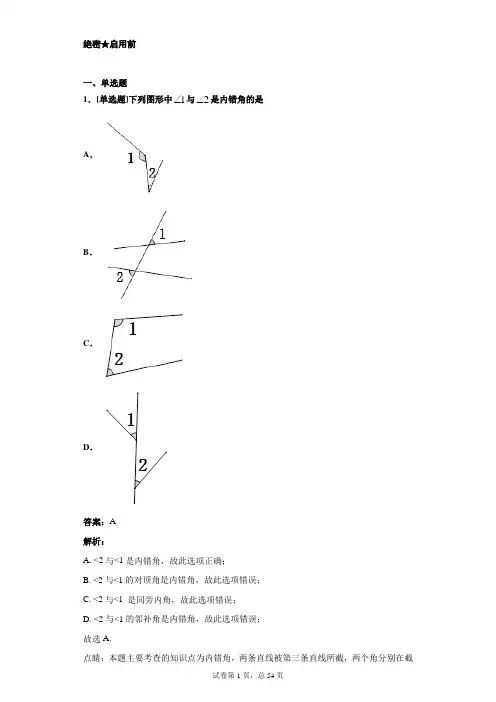
绝密★启用前一、单选题1．[单选题]下列图形中1∠与2∠是内错角的是A ．B ．C ．D ．答案：A 解析：A. <2与<1是内错角，故此选项正确；B. <2与<1的对顶角是内错角，故此选项错误；C. <2与<1 是同旁内角，故此选项错误；D. <2与<1的邻补角是内错角，故此选项错误；线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角.掌握内错角的定义是解答本题的关键.2．[单选题]已知如图AB 、BE 被AC 所截，下列说法不正确的是（ ）A ．1∠与2∠是同旁内角B ．1∠与ACE ∠是内错角C ．B 与ACB ∠是同位角D ．1∠与3∠不是同位角 答案：C 解析： 解析：根据同位角、内错角、同旁内角的定义可以直接得到答案. 【详解】 解：A. 1∠与2∠是同旁内角，正确但不符合题意；B. 1∠与ACE ∠是内错角，正确但不符合题意；C. B ∠与ACB ∠是同位角，错误符合题意；D.1∠与3∠不是同位角，正确但不符合题意.故选：C. 【点睛】本题主要考查了三线八角.3．[单选题]如图，∠1与∠2不能构成同位角的图形的是（ ）A ．B．C．D．答案：D解析：解析：根据同位角的定义来分析判断即可，两条直线被第三条直线所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角.【详解】由同位角的定义可知图A、B、C中的∠1和∠2可以构成同位角，D中的∠1和∠2构不成同位角.故本题答案为：D.【点睛】同位角的定义是本题的考点，根据同位角的定义正确识别同位角是解题的关键. 4．[单选题]如图，下列说法错误的是（）A．∠1与∠3是对顶角B．∠3与∠4是内错角C．∠2与∠6是同位角D．∠3与∠5是同旁内角答案：C解析：根据对顶角定义、内错角定义、同位角定义、同旁内角定义进行分析即可．【详解】A、∠1与∠3是对顶角，故A说法正确；B、∠3与∠4是内错角，故B说法正确；C、∠2与∠6不是同位角，故C说法错误；D、∠3与∠5是同旁内角，故D说法正确；故选：C．【点睛】本题考查对顶角、内错角、同位角和同旁内角的定义，掌握其定义是选择本题答案的关键．5．[单选题]下列选项中，∠ 5和∠6不是同旁内角的是（）A．B．C．D．答案：B解析：根据同旁内角的定义:两条直线被第三条直线所截，在截线同旁，且在被截线之内的两角，叫做同旁内角.进行解答【详解】A. ∠5和∠6是同旁内角,不合题意,故此选项错误.B.∠5和∠6不是同旁内角,符合题意,故此选项正确C.∠5和∠6是同旁内角,不合题意,故此选项错误D.∠5和∠6是同旁内角,不合题意,故此选项错误【点睛】本题考查同旁内角的定义,理解掌握同旁内角定义是解题关键6．[单选题]如图，直线1l和2l被直线3l所截，则（）A ．1∠和2∠是同位角B ．1∠和2∠是内错角C ．1∠和3∠是同位角D ．1∠和3∠是内错角 答案：C 解析：根据同位角和内错角的定义进行分析即可． 【详解】同位角是位于两直线及截线的同侧，内错角是位于两直线内侧及截线两侧，故1∠和3∠是同位角； 故选：C ． 【点睛】本题考查了同位角和内错角的判断，熟练掌握基本概念是解决这类问题的关键． 8．[单选题]如图，点D 、E 分别为三角形ABC 边BC 、AC 上一点，作射线DE ，则下列说法错误的是（ ）A ．∠1与∠3是对顶角B ．∠2与∠A 是同位角C ．∠2与∠C 是同旁内角D ．∠1与∠4是内错角解析：根据同位角、内错角以及同旁内角的概念进行判断．【详解】解：A、∠1与∠3是对顶角，说法正确；B、∠2与∠A是同位角，说法正确；C、∠2与∠C是同旁内角，说法正确；D、∠2与∠4是内错角，说法错误．故选：D．【点睛】考查了同位角、内错角以及同旁内角，解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．9．[单选题]如图，下列结论正确的是（）.A．∠5与∠2是对顶角；B．∠1与∠3是同位角；C．∠2与∠3是同旁内角；D．∠1与∠2是同旁内角.根据对顶角即三线八角的特征可得∠1与∠2是同旁内角，故选D。

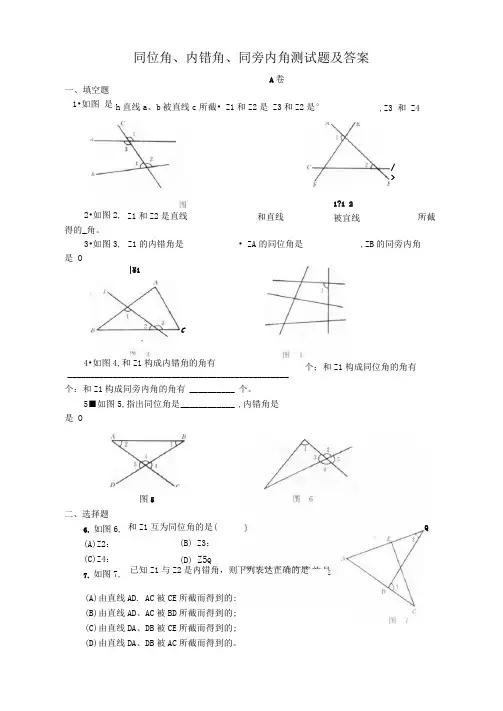
同位角、内错角、同旁内角测试题及答案A卷h直线a、b被直线c所截• Z1和Z2是 Z3和Z2是°|¥14•如图4,和Z1构成内错角的角有_________________________________________________个：和Z1构成同旁内角的角有 __________ 个。

5■如图5,指出同位角是____________ ,内错角是是 O/>1?1 2被宜线2•如图2,得的_角。

3•如图3,是 OZ1和Z2是直线Z1的内错角是和直线所截• ZA的同位角是,ZB的同旁内角图5二、选择题6.如图6,(A)Z2：(C)Z4：7.如图7,Q 和Z1互为同位角的是((B) Z3：(D) Z5Q已知Z1与Z2是内错角，则下列表达正确的是(A)由直线AD. AC被CE所截而得到的:(B)由直线AD、AC被BD所截而得到的;(C)由直线DA、DB被CE所截而得到的;(D)由直线DA、DB被AC所截而得到的。

一、填空题1•如图是,Z3 和Z4个；和Z1构成同位角的角有C8•在图8中1和2是同位角的有(RI(A)(1). (2)：9.如图9,在指明的角中，下列说法不正确的是()(A) 同位角有2对；(C)内错角有4对：(B)(2)、(3)：(D)(2)、(4)。

(B)同旁内角有5对：(D)Z1和Z4不是内错角。

(B)4：⑷3：三、简答题11.如图11(1)说出Z1与Z2互为什么角?(2)写出与Z1成同位角的角；(3)写出与Z1成内错角的角。

)对内错角(05：(D)6。

12.如图12(D说出ZA与Z1互为什么角?(2) ZB与Z2是否是同位角；⑶写出与Z2成内错角的角013.如图13.指出同位角、内错角、同旁内角.B卷一、填空题1 •如图1, Z1和Z2可以看作直线和直线被直线所截得的角。

截得的 ________ 角。

3•如图3,直线DE、BC被直线AC所截得的内错角是宜线、被直线_______ 所截得的_______ 角°图34•如图4,与ZEFC构成内错角的是________的是5.如图5,与Z1构成内错角的角有_个：与Z1构成同旁内角的角有 __________ 个。

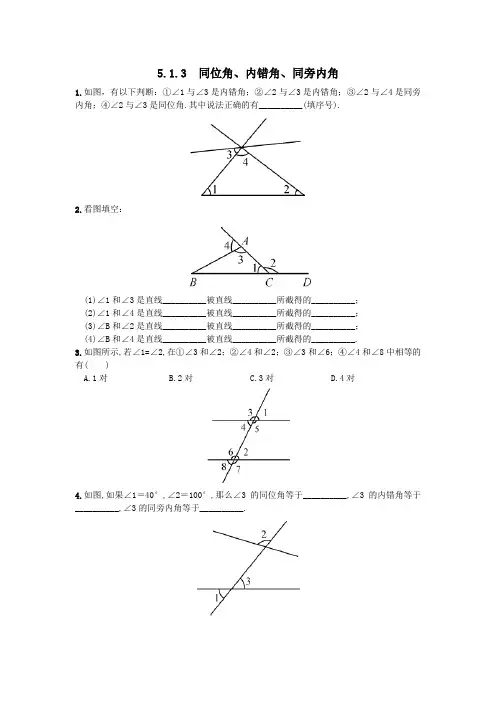
5.1.3 同位角、内错角、同旁内角1.如图，有以下判断：①∠1与∠3是内错角；②∠2与∠3是内错角；③∠2与∠4是同旁内角；④∠2与∠3是同位角.其中说法正确的有__________(填序号).2.看图填空：(1)∠1和∠3是直线__________被直线__________所截得的__________；(2)∠1和∠4是直线__________被直线__________所截得的__________；(3)∠B和∠2是直线__________被直线__________所截得的__________；(4)∠B和∠4是直线__________被直线__________所截得的__________.3.如图所示,若∠1=∠2,在①∠3和∠2；②∠4和∠2；③∠3和∠6；④∠4和∠8中相等的有( )A.1对B.2对C.3对D.4对4.如图,如果∠1＝40°,∠2＝100°,那么∠3的同位角等于__________,∠3的内错角等于__________,∠3的同旁内角等于__________.5.如图，下列说法错误的是( )A.∠1和∠3是同位角B.∠A和∠C是同旁内角C.∠2和∠3是内错角D.∠3和∠B是同旁内角6.如图所示，∠B与∠CAD是由直线__________和直线__________被直线__________所截得到的__________角.7.如图，__________是∠1和∠6的同位角，__________是∠1和∠6的内错角，__________是∠6的同旁内角.8.根据图形说出下列各对角是什么位置关系？(1)∠1和∠2；(2)∠1和∠7；(3)∠3和∠4；(4)∠4和∠6；(5)∠5和∠7.9.如图，∠1和∠2是哪两条直线被哪一条直线所截形成的？它们是什么角？∠1和∠3是哪两条直线被哪一条直线所截形成的？它们是什么角？10.探究题：(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对；(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对；(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对.(用含n的式子表示)5.2平行线及其判定参考答案1.①③2.(1)AB，BC AC 同旁内角(2)AB，BC AC 同位角(3)AB，AC BC 同位角(4)AC，BC AB 内错角3.C4.80° 80° 100°5.A6.BC AC BD 同位7.∠3 ∠5 ∠48.(1)∠1和∠2是同旁内角；(2)∠1和∠7是同位角；(3)∠3和∠4是内错角；(4)∠4和∠6是同旁内角；(5)∠5和∠7是内错角.9.∠1和∠2是直线EF，DC被直线AB所截形成的同位角，∠1和∠3是直线AB，CD被直线EF所截形成的同位角.10.(1)4 2 2(2)12 6 6(3)2n(n-1) n(n-1) n(n-1)。

2019年4月16日初中数学作业学校: ______________姓名： ______________ 班级：______________ 考号：______________一、单选题1.已知/ 1和/ 2是同旁内角，/ 1=60。

，/ 2等于（）A. 140°B. 120°C. 60°D.无法确定【答案】D【解析】【分析】本题只是给出两个角的同旁内角关系，没有两直线平行的条件，故不能判断两个角的数【详解】解：同旁内角只是一种位置关系，两直线平行时同旁内角互补，不平行时无法确定同旁内角的大小关系，故选D .【点睛】特别注意，同旁内角互补的条件是两直线平行.【分析】本题需先根据同位角的定义进行筛选，即可得出答案.【详解】A、•••根据同位角的定义得:/ 1与/ 2不是同位角，故本选项错误；B、•根据同位角的定义得:/1与/2是同位角，故本选项正确；C、•根据同位角的定义得:【解析】/ 1与/ 2不是同位角，故本选项错误；D、•••根据同位角的定义得:/ 1与/ 2不是同位角，故本选项错误.故选B.【点睛】本题主要考查了同位角，在解题时要根据同位角的定义进行筛选是本题的关键.【答案】C【解析】【分析】根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角进行分析即可.【详解】如图①，/ 1、/ 2是直线m与直线n被直线p所截形成的同位角，故①符合题意；如图②，/ 1、/ 2是直线p与直线q被直线r所截形成的同位角，故②符合题意；如图③，/ 1是直线d与直线e构成的夹角，/ 2是直线g与直线f形成的夹角，/ 1与/2不是同位角，故③不符合题意；如图④，/ 1、/ 2是直线a与直线b被直线c所截形成的同位角，故④符合题意.故选C.【点睛】本题考查了同位角，关键是掌握同位角的边构成“ F “形，内错角的边构成“ Z “形，同3•如图所示，Z1和Z2是同位角的是（A .②③B.①②③ C.①②④D.①④P旁内角的边构成“ U ”形.4•下列所示的四个图形中，/1和/ 2是同位角的是（）【答案】D【解析】【分析】根据同位角，内错角，同旁内角的概念解答即可.【详解】/ 1和/ 2是同位角的是①②④.故选D.【点睛】本题考查了同位角，内错角，同旁内角的概念，关键是根据同位角，内错角，同旁内角的概念解答.【解析】【分析】根据同位角的特征：两条直线被第三条直线所截形成的角中，两个角都在两条被截直线的同侧，并且在第三条直线（截线）的同旁，由此判断即可.【详解】解：A、B、D中/ 1和/ 2是同位角；C、/ 1和/ 2不满足两条直线被第三条直线所截形成的角，所以不是同位角；故选：C.【点睛】本题考查三线八角中的某两个角是不是同位角，同位角完全由两个角在图形中的相对位置决定•在复杂的图形中判别同位角时，应从角的两边入手，具有上述关系的角必有两C.①③④D.①②④1和/ 2的关系是（A .对顶角【答案】DC.内错角D .同旁内角边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即 为被截的线•同位角的边构成“F 形.B. Z 1和/ 4是内错角D .Z C 和/ A 不是同旁内角【答案】D 【解析】【分析】线（截线）的同旁，则这样一对角叫做同位角；两条直线被第三条直线所截形成的角中, 若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角；两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第 三条直线（截线）的两旁，则这样一对角叫做内错角 【详解】A. / 1和/B 是DE 与BC 被AB 所截得到的同位角，正确；B. / 1和/ 4是AB 与AC 被DE 所截得到的内错角，正确；C. / 3和/ B 是DE 与BC 被AB 所截得到的同旁内角，正确；D. / C 和/A 是AB 与BC 被AC 所截得到的同旁内角，故不正确；故选D. 【点睛】本题考查了同位角、内错角、同旁内角的定义，熟练掌握三种角的特征是解答本题的关 键•两条直线被第三条直线所截形成的角中， 若两个角都在两直线的同侧，并且在第三条直C .Z 3和/ B 是同旁内角B .同位角解析】【分析】结合图形，根据同位角、内错角、同旁内角的概念进行判断即可.【详解】观察图形可知，/ 1和/ 2两个角都在两被截直线b和c的内侧，并且在第三条直线a（截线）的同旁，故/ 1和/2是直线b、c被a所截而成的同旁内角，故选D ．【点睛】本题考查了“三线八角”，熟练掌握同位角、内错角、同旁内角的图形特征是解题的关键8./ 1与/ 2是内错角，/ 仁30 °则/ 2的度数为（）A. 30 °B. 150 °C. 30 或150 °D.不能确定【答案】D【解析】【分析】两直线平行时内错角相等，不平行时无法确定内错角的大小关系，据此分析判断即可得【详解】内错角只是一种位置关系，并没有一定的大小关系，只有两直线平行时，内错角才相等，故选D .【点睛】本题考查了三线八角，明确同位角、内错角、同旁内角只是两个角的一种位置关系，而没有一定的大小关系是解此类问题的关键.9 .两条直线被第三条直线所截，若/ 1与/ 2是同旁内角，且/ 仁70o,则（）A. Z 2=70oB.Z 2=110oC. Z 2=70o或Z 2=110oD.Z 2的度数不能确定【答案】D【解析】【分析】两直线被第三条直线所截，只有当两条被截直线平行时，内错角相等，同位角相等，同旁内角互补．不平行时以上结论不成立．【详解】】解：因为两条直线的位置关系不明确，所以无法判断Z 1和Z 2大小关系•故选：D ．【点睛】本题考查平行线的性质，注意性质定理的条件是两直线平行.10 .如图，点0是直线AB上一点，0E , OF分别平分/ AOC和/ BOC ,当0C的位置发生变化时(不与直线AB重合)，那么/ EOF的度数()A .不变，都等于90 °B. 逐渐变大C. 逐渐变小D. 无法确定【答案】A【解析】【分析】由OE与OF为角平分线，利用角平分线定义得到两对角相等，由平角的定义及等式的性质即可求出所求角的度数【详解】•••OE、OF分别是/ AOC、/ BOC的角平分线，•••/ AOE =Z COE , / COF = / BOF , AOC + Z COB =Z AOE + Z COE + Z COF+ Z BOF = 180°, ••• 2 (Z COE + Z COF)= 180°即Z COE + Z COF = 90°, •••/ EOF = Z COE+ Z COF = 90°•故选A.【点睛】本题主要考查角平分线的性质和平角的定义，得出 2 ( Z COE + Z COF )= 180°是解题的关键.11.如图，直线AB , CD , EF相交于点A. Z BOFO,则Z COF的一个邻补角是B .Z DOFC.Z AOED.Z DOE【答案】B【解析】【分析】根据邻补角的定义解答即可【详解】两个角有一条公共边，它们的另一条边互为反向延长线，具有这种关系的两个角，叫做邻补角，因此/ COF 的一个邻补角是/ DOF.故选B.【点睛】本题主要考查邻补角的定义，熟记邻补角的定义是解答的关键【解析】【分析】根据内错角的定义找出即可.【详解】由内错角的定义可得A、B、C中/3与/4是内错角，D中的/3与/4不是内错角故选D.【点睛】本题考查了同位角、内错角、同旁内角，熟记内错角的定义是解题的关键.【答案】B【解析】【分析】根据同旁内角的定义，逐条分析四个选项，即可得出结论.【答案】DA.13 .如图，/ 1,D.【详解】A、 /1和/2是同旁内角；B、 /1和/2不是同旁内角;C、 /1和/2是同旁内角；D、 / 1和/ 2是同旁内角.故选：B.【点睛】本题考查了同旁内角的定义，解题的关键是根据同旁内角的定义去逐条分析选项. 本题属于基础题，难度不大，解决该题型题目时，分析图形寻找两角的关系是关键.14 .下列各图中，/A.【答案】B【解析】【分析】根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角进行分析即可.【详解】根据同位角定义可得B不是同位角，故选：B.【点睛】此题主要考查了同位角，关键是掌握同位角的边构成“F形，内错角的边构成“ Z形，同旁内角的边构成“ U形.、填空题15 •同位角的特征是在两条线被截线的_______________________ ,并且在截线的______________ ，如图,【分析】两条直线被第三条直线所截形成的角中， 若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角； 结合题中所给的图形，运用同位角的定义即可求解 【详解】解：同位角的特征是在两条被截线的同一方， 并且在截线的同一侧， 如图，/ 1和/ 2是同位角• 【点睛】本题考查同位角的定义，熟悉掌握是解题关键•16 •如图，直线11, 12被直线13所截，则图中同位角有 _______________ 对.【答案】4 【解析】 【分析】直接利用两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角，进而得出答案./ 1和/ 3, / 2和/ 4, / 8和/ 6, / 7和/ 5,都是同位角，一共有 4对. 故答案为：4. 【点睛】本题考查的知识点是同位角的定义，解题关键是正确把握定义.1 , 2.【解析】17 .如图，/ F的内错角有______________________ .【答案】/ AEF 和/ ADF【解析】【分析】根据内错角的定义，结合图形寻找符合条件的角.【详解】根据内错角的定义可知：与/ F 互为内错角的只有/ AEF 和/ ADF .故答案为：/ AEF 和/ ADF .【点睛】本题考查的知识点是内错角的定义，解题关键是熟记内错角的定义.【解析】【分析】根据三线八角的概念，以及同旁内角的定义求得•【详解】如图所示，/ DCB 和/ABC 具有公共边 BC ,另外两条边分别在直线 CD 和AB 上，故/ DCB 和/ ABC 是直线DE 和AB 被直线BC 所截而成的同旁内角.故答案为： DE , AB , BC ,同旁内.【点睛】本题考查了三线八角的概念中的同旁内角的概念19 .如图，直线AB ,CD 相交于点0,0E 丄AB ,0为垂足，/ EOD=26 °，则/ AOC=【答案】64°116°【解析】 【分析】 根据垂线的定义进行作答_______ 所截而成的 和_______被直线 / C0B=【详解】由0E 丄AB，得到/ AOE=90 ,所以/ AOC=180 - / EOD- / AOE=64 ;因为/ BOD=64 , /COB=180 - / BOD= 116 .【点睛】本题考查了垂线的定义，熟练掌握垂线的定义是本题解题关键20 .如图：a// b ,图中的 // 1 , // 2 , // 3 , // 4 , // 5, // 6 , // 7 中同位角有________________ 对.【答案】3【解析】【分析】根据两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角•同位角的边构成“F形作答.【详解】观察图形可知：/ 1的同位角是/ 4, / 3的同位角是/ 5 , / 7的同位角是/ 6 ,•••图中同位角有3个.故答案为：3.【点睛】此题主要考查同位角的概念，有以下几个要点：1、分清截线与被截直线；2、两个相同，在截线同旁，在被截直线同侧.21.如图，直线MN分别交直线AB , CD于E , F ,其中，// AEF的对顶角是// ____________________ , // BEF的同位角是// ________________ .【解析】【答案】BEM DFN.【分析】 / AEF与/ BEM有公共顶点，/ BEM的两边是/ AEF的两边的反向延长线，所以是对顶角；/ BEF与/ DFN ,在截线MN的同侧，被截线AB、CD的同旁，所以是同位角.【详解】/ AEF的对顶角是/ BEM , / BEF的同位角是/ DFN .故答案为：BEM , DFN .【点睛】本题考查对顶角与同位角的概念，是需要熟记的内容.三、解答题22 .如图，AB、CD相交于点O, 0M平分/ B0D，/ MON是直角，/ AOC =50 °(1) 求/ AON的度数；(2) 求/ DON的邻补角的度数.【分析】(1)根据角平分线的定义求出/ M OB的度数，根据邻补角的性质计算即可.(2)根据题意得到：/ CON为/ DON的邻补角.【详解】解：(1 )•••/ AOC+Z AOD = Z AOD + Z BOD=180°,•••/ BOD= / AOC=50°,•/ OM 平分/ BOD ,•••/ BOM= / DOM =25°,又由/ MON=90°,•••/ AON=180°- (/ MON + / BOM) =180°- (90°+25°) =65°(2)vZ AON=65°, / AOC=50°•••/ CON= / AON+ / AOC=115°,即/ DON 的邻补角的度数为115°【点睛】本题考查的是邻补角的概念以及角平分线的定义，掌握邻补角的性质是邻补角互补是解【解析】)115°题的关键.23 .如图，直线a, b被直线I所截，已知/ 1 = 40 °试求/ 2的同位角及同旁内角的度【分析】首先找出/2的同位角与同旁内角；再结合已知角的度数，找出待求角与已知角的关系，即可求解•【详解】解：1= 40°,.•./ 3=/ 1= 40°,/ 4= 180°—/ 1= 140°,即/ 2的同位角是140。

同位角、内错角、同旁内角训练题及答案一、选择题（共10小题；共30分）1. 如图所示，已知AB∥CD，与∠1是同位角的角是A. ∠2B. ∠3C. ∠4D. ∠52. 在同一平面内的三条直线，如果要使其中两条且只有两条平行，那么它们 ( )A. 有三个交点B. 只有一个交点C. 有两个交点D. 没有交点3. 下列说法中正确的有 ( )A. 连接两点的线段叫做两点间的距离B. 过一点有且只有一条直线与已知直线平行C. 若AB=BC，则点B是AC的中点D. 直线AC和直线CA是同一条直线4. 如图，把教室中墙壁的棱看做直线的一部分，那么下列表示两条棱所在的直线的位置关系不正确的是A. AB⊥BCB. AD∥BCC. CD∥BFD. AE∥BF5. 已知直线a，b，c，d，下面推理正确的是 ( )A. 因为a∥d，b∥c，所以c∥dB. 因为a∥c，b∥d，所以c∥dC. 因为a∥b，a∥c，所以b∥cD. 因为a∥b，c∥d，所以a∥c6. 如图所示，∠1和∠2是同位角的有A. ①②B. ①③C. ①④D. ②③7. 如图，下列判断不正确的是A. ∠B与∠A是同旁内角B. ∠C与∠1是内错角C. ∠2与∠3是内错角D. ∠B与∠1是同位角8. 在同一平面内，下列说法正确的是 ( )A. 不相交的两条直线是平行线B. 不相交的两条射线是平行线C. 不相交的两条线段是平行线D. 不平行的两条线段一定相交9. 三条直线a，b，c，若a∥c，b∥c，则a与b的位置关系是 ( )A. a⊥bB. a∥bC. a⊥b或a∥bD. 无法确定10. 下列结论中，不正确的是 ( )A. 两点确定一条直线B. 等角的余角相等C. 过一点有且只有一条直线与已知直线平行D. 两点之间的所有连线中，线段最短二、填空题（共6小题；共18分）11. 在同一平面内，两条直线的位置关系只有和两种．12. 平行公理的推论是：如果两条直线都与，那么这两条直线也．即三条直线a，b，c，如果a∥b，b∥c，那么．13. 若AB∥CD，AB∥EF，则∥，理由是．14. 下图有对内错角．15. 已知平面内四条直线共有三个交点，则这四条直线中最多有条平行线．16. 如图，平行直线AB、CD与相交直线EF、GH相交，图中的同旁内角共有对．三、解答题（共6小题；共52分）17. 如图所示，a∥b，b∥c，d与a相交于点M．(1) 试判断直线a，c的位置关系，并说明理由；(2) 判断c与d，b与d的位置关系，并说明理由．18. 工人师傅在铺设电缆时，为了检验三条电缆线是否平行，只检查了其中两条电缆线是否与第三条电缆线平行，你认为这种做法正确吗？请作出合理解释．19. 如图，指出下列各组角是由哪两条直线被哪一条直线所截得的，并说出它们是什么角？∠1和∠2，∠2和∠6，∠4和∠7，∠3和∠5．20. 如图，直线DE，BC被直线AB所截．(1) ∠1与∠2，∠1与∠3，∠1与∠4各是什么角？(2) 如果∠1=∠4，那么∠1和∠2相等吗？∠1和∠3呢？为什么？21. 在同一平面内有n条直线，当n=1时，如图（1），一条直线将一个平面分成两个部分；当n=2时，如图（2），两条直线将一个平面最多分成四个部分．(1) 在作图区分别画出当n=3时，三条直线将一个平面分成最少部分和最多部分的情况；(2) 当n=4时，请写出四条直线将一个平面分成最少部分的个数和最多部分的个数；(3) 若n条直线将一个平面最多分成a n个部分，(n+1)条直线将一个平面最多分成a n+1个部分，请写出a n，a n+1，n之间的关系式．22. 我们知道相交的两直线的交点个数是1，记两平行直线的交点个数是0；这样平面内的三条平行线它们的交点个数就是0，经过同一点的三直线它们的交点个数就是1；依次类推⋯．(1) 请你画图说明同一平面内的五条直线最多有几个交点？(2) 平面内的五条直线可以有4个交点吗？如果有，请你画出符合条件的所有图形；如果没有，请说明理由．(3) 在平面内画出10条直线，使交点个数恰好是31．答案第一部分1. D2. C3. D4. C5. C6. A7. B8. A9. B 10. [2]第二部分11. 相交；平行12. 第三条直线平行；互相平行；a∥c13. CD；EF；如果两条直线都与第三条直线平行，那么这两条直线也互相平行14. 2415. 316. 16第三部分17. (1) 因为a∥b，b∥c，所以a∥c．理由：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．17. (2) 因为d，a都过M点且a∥c，所以d与c相交；同理：b与d相交．理由：经过直线外一点，有且只有一条直线与这条直线平行．18. (1) 正确．如果两条直线都与第三条直线平行，那么这两条直线也互相平行．19. (1) ∠1和∠2是同位角，是直线BD，DE被AB所截得到的；∠2和∠6是内错角，是直线AB，CD被BD所截得到的；∠4和∠7是同旁内角，是直线AB，BC被CE所截得到的；∠3和∠5是同旁内角，是直线DE，DC被CE所截得到的．20. (1) ∠1与∠2是内错角，∠1与∠3是同旁内角，∠1与∠4是同位角．20. (2) 如果∠1=∠4，那么∠1和∠2相等，∠1和∠3互补．理由是：因为∠1=∠4，又根据对顶角相等知∠2=∠4，所以∠1=∠2．因为∠3和∠4互为补角，所以∠3+∠4=180∘，所以∠1+∠3=180∘，即∠1和∠3互补．21. (1)21. (2) 最少5部分，最多11部分．21. (3) a n+1−a n=n+122. (1) 如图，最多有10个交点．22. (2) 可以有4个交点，有3种不同的情形，如图．22. (3) 在平面内画出10条直线，使交点个数恰好是31，如图。

同位角、内错角、同旁内角练习【同步达纲练习】1.填空(1)如图2-43，直线AB、CD被DE所截，则∠1和是同位角，∠1和是内错角，∠1和是同旁内角，如果∠1=∠5.那么∠1 ∠3.（2）上题中（图2-43）如果∠5=∠1，那么∠1=∠3的推理过程如下，请在括号内注明理由：∵∠5=∠1（）又∵∠5=∠3（）∴∠1=∠3（）（3）如图2-44，∠1和∠4是AB、被所截得的角，∠3和∠5是、被所截得的角，∠2和∠5是、所截得的角，AC、BC被AB所截得的同旁内角是 .∠（4）如图2-45，AB、DC被BD所截得的内错角是，AB、CD被AC所截是的内错角是，AD、BC被BD所截得的内错角是，AD、BC被AC所截得的内错角是 .2.选择题（1）如图2-46，∠1与∠2是同位角的个数有（）A.1个B.2个C.3个D.4个（2）如图2-47，（）是内错角A. ∠1和∠2B. ∠3和∠4C. ∠2和∠3D. ∠1和∠4（3）如图2-48，图中的同位角的对数是（）A.4B.6C.8D.123.如图2-49，已知∠1的同旁内角等于57°28′，求∠1的内错的度数.【素质优化训练】1.如图2-50图中,共有几对内错角?这几对内错角分别是哪两条直线被哪一条直线所截构成的?2.如图2-51,直线AB、CD被EF所截，如果∠1与∠2互补，且∠1=110°，那么∠3、∠4的度数是多少？参考答案【同步达纲练习】1．（1）∠3，∠5，∠2= （2）已知，对顶角相等，等量代换（3）CD，BE，同位角；AB，BC，AC，同旁内角 AB，CD，AC，内错角；∠4和∠5 （4）∠1和∠5，∠4和∠8，∠6和∠2，∠3和∠72．（1）D （2）B （3）B 3.122°32′【素质优化训练】1．BC、BE被DF截得的两对内错角；∠DFB和∠CDF；∠FDB和∠FDB；AC、AD被BE截得的两对内错角：∠AFE和∠CEF，∠AEF和∠EFD2．∠3=70°，∠4=70°。

同位角、内错角、同旁内角经典练习题1.如图，点D E ，分别为ABC △边BC AC ，上一点，作射线DE ，则下列说法错误的是（ ）第1题图 第2题图A ．1∠与3∠是对顶角B ．2∠与A ∠是同位角C ．2∠与C ∠是同旁内角D ．1∠与4∠是内错角2.如图，已知1∠与2∠是内错角，则下列表述正确的是( )A.由直线AD BC ，被AC 所截而得到的B.由直线AB CD ，被BC 所截而得到的C.由直线AB CD ，被AC 所截而得到的D.由直线AD BC ，被CD 所截而得到的3.如图，直线AD BE ，被直线BF 和AC 所截，则1∠的同位角和5∠的内错角分别是( )A.42∠∠，B.26∠∠，C.54∠∠，D.24∠∠，4.如图，B ∠的同位角可以是( )A.1∠B.2∠C.3∠D.4∠5.如图所示，以下几种说法，其中正确的个数是( )①3∠和4∠是同位角；②6∠和7∠是同位角；③4∠和5∠是内错角；④2∠和5∠是同旁内角⑤2∠和7∠是同位角；⑥1∠和2∠是同位角A.3B.4C.5D.66.如图所示，与∠A 是同旁内角的角共有 个.7.如图，2∠的内错角是 ，3∠与B ∠是 角，B ∠的同旁内角是 .第7题图第8题图8.如图（1）找出直线DC AC ，被直线BE 所截形成的同旁内角； （2）指出DEF ∠与CFE ∠是由哪两条直线被哪一条直线所截形成的什么角；（3）试找出图中与DAC ∠是同位角的所有角.答案以及解析1.答案：D解析：根据同位角、内错角以及同旁内角的概念进行判断：A 、B 、C 、正确D 错误.2.答案：C解析：因为1∠的两边为AB AC ，，2∠的两边为AC CD ，，所以1∠与2∠是由直线AB CD ，被AC 所而得到的，故选C3.答案：B解析：由题意，知1∠的同位角是25∠∠，的内错角是6∠，故选B.4.答案：D解析：根据同位角的特征可知，∠B 的同位角可以是4∠.故选D.5.答案：B解析：根据同位角、内错角、同旁内角的特征可知，3∠和4∠是同位角，1∠和2∠是同位角，4∠和5∠是内错角，2∠和5∠是同旁内角，6∠和7∠不是同位角，2∠和7∠不是同位角则正确的为③④①，共4个，故选B6.答案：4解析：与A ∠是同旁内角的有,,,ABC ADC ADE AED ∠∠∠∠,共4个.7.答案：C ∠ 内错 1∠或DAB ∠或C ∠解析：2∠和C ∠在被截线AD 和BC 的内部，截线AC 的两侧，故2∠的内错角是C ∠；3∠与B ∠在被截线AE 和BC 的内部，截线AB 的两侧，故3∠与B ∠是内错角；B ∠的同旁内角是1∠或DAB ∠或C ∠8.答案：解:（1）FBC ∠和CFB ∠，DFB ∠和FBA ∠是直线DC AC ，被直线BE 所截形成的同旁内角.（2）DEF ∠与CFE ∠是由直线AG DF ，被直线EF 所截形成的内错角.（3）DAC ∠的同位角有EBH DCH EDF GEF ∠∠∠∠，，，.。

5.1.3《同位角、内错角、同旁内角》重难点题型专项练习考查题型一 同位角典例1．（2022·广西贺州·统考三模）如图，直线a 、b 被直线c 所截，∠1的同位角是（ ）A ．∠2B ．∠3C ．∠4D ．∠5【答案】A【分析】根据同位角的定义逐个判断即可．【详解】解：A 、∠2与∠1是同位角，故本选项符合题意；B 、∠3与∠1不是同位角，故本选项不符合题意；C 、∠4与∠1不是同位角，故本选项不符合题意；D 、∠5与∠1不是同位角，故本选项不符合题意；故选：A ．【点睛】本题考查了同位角，内错角，同旁内角等知识点，能熟记同位角的定义是解此题的关键． 变式1-1．（2022·广西柳州·统考一模）如图，与1∠是同位角的是（ ）A ．2∠B ．3∠C ．4∠D ．5∠【答案】C【分析】根据同位角的定义：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角即可求解．【详解】解：观察图形可知，与∠1是同位角的是∠4．故选：C ．【点睛】本题考查了同位角、内错角、同旁内角，三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．变式1-2．（2022·广西贺州·统考中考真题）如图，直线a ，b 被直线c 所截，下列各组角是同位角的是（ ）A ．1∠与2∠B ．1∠与3∠C ．2∠与3∠D ．3∠与4∠【答案】B【分析】两条线a 、b 被第三条直线c 所截，在截线的同旁，被截两直线的同一方，把这种位置关系的角称为同位角，据此作答即可．【详解】解：∠1与∠2是对顶角，选项A 不符合题意；∠1与∠3是同位角，选项B 符合题意；∠2与∠3是内错角，选项C 不符合题意；∠3与∠4是邻补角，选项D 不符合题意；故选：B ．【点睛】此题考查了同位角、内错角、同旁内角，熟记同位角、内错角、同旁内角的定义是解题的关键． 变式1-3．（2022秋·浙江杭州·七年级校考期中）如图，∠1和∠2是同位角的是（ ）．A ．B ．C ．D ．【答案】C 【分析】根据同位角的定义，逐一判断选项，即可．【详解】解：A 、∠1和∠2不是同位角，故选项A 不合题意；B 、 ∠1和∠2 不是同位角，故选项B 不合题意；C 、 ∠1和∠2 是同位角，故选项C 符合题意；D 、∠1和∠2 不是同位角，故选项D 不合题意．故答案为：C ．【点睛】本题主要考查同位角的定义，掌握“两条直角被第三条直线所截，在两条直线的同侧，在第三条直线的同旁的两个角，叫做同位角”，是解题的关键．考查题型二 内错角典例2．（2022秋·江苏淮安·七年级校考阶段练习）下列四个图形中，1∠和2∠是内错角的是（ ） A ． B ．C ．D ．【答案】B【分析】根据内错角的概念：处于两条被截直线之间，截线的两侧，再逐一判断即可．【详解】解：A 、∠1与∠2不是内错角，选项不符合题意；B 、∠1与∠2是内错角，选项符合题意；C 、∠1与∠2不是内错角，选项不符合题意；D 、∠1和∠2不是内错角，选项不符合题意；故选：B ．【点睛】本题考查了内错角，关键是根据内错角的概念解答．注意：内错角的边构成“Z”形．变式2-1．（2022秋·湖北武汉·七年级校考阶段练习）如图，下列各组角中，互为内错角的是（）A ．1∠与3∠B ．2∠与5∠C ．3∠与5∠D ．4∠与5∠【答案】C【分析】根据内错角的定义结合具体的图形进行判断即可．【详解】解：A. 1∠与3∠是直线a ，直线b 被直线c 所截的同位角；B. 2∠与5∠不具备特殊位置关系；C.3∠和5∠是直线a ，直线b 被直线c 所截的内错角；∠是直线a，直线b被直线c所截的同旁内角；D. 4∠和5故选：C．【点睛】本题考查内错角，理解内错角的定义是正确判断的前提．两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．变式2-2．（2022秋·新疆乌鲁木齐·七年级乌鲁木齐市第四十一中学校考期末）如图中1∠是内错角是∠与2（）A．①②B．②③C．③④D．②④【答案】D【分析】根据内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角进行分析即可．【详解】解：由内错角的定义可知，图②和图④中，1∠是内错角，∠和2故选：D．【点睛】本题考查了内错角、同位角、同旁内角的概念，同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．变式2-3．（2022秋·安徽安庆·七年级校考阶段练习）如图，直线a，b被直线c所截，则∠1与∠2是（）A．内错角B．同位角C．对顶角D．邻补角【答案】A【分析】根据同位角、内错角、同旁内角的定义逐个判断即可．【详解】解：直线a，b被直线c所截，则∠1与∠2是内错角．故选：A ．【点睛】本题考查了同位角、内错角、同旁内角的定义，能理解同位角、内错角、同旁内角的定义是解此题的关键，注意：数形结合思想的运用．考查题型三 同旁内角典例3．（2022秋·浙江宁波·七年级校考期中）如图，直线AB 、CD 被直线EF 所截，则∠1的同旁内角是（ ）A ．∠2B ．∠3C ．4∠D ．5∠【答案】B【分析】根据同旁内角的定义，结合已给图形分析，即可得到答案．【详解】解：由同旁内角的定义知，∠1和∠3在直线AB 和CD 之间，且在直线EF 的同一侧，所以，∠1的同旁内角是∠3．故选：B【点睛】本题考查同旁内角的定义，解题的关键是结合图形，牢记定义内容去分析判断．变式3-1．（2022秋·湖北鄂州·七年级统考期中）如图，与2∠互为同旁内角的角是（ ）A ．1∠与5∠B ．8∠与9∠C ．3∠与12∠D ．7∠与10∠【答案】B【分析】根据两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角进行解答即可．【详解】解：根据题意得： 9∠与2∠互为同旁内角，8∠与2∠互为同旁内角．故选：B【点睛】本题考查了同旁内角的定义．注意在截线的同旁找同旁内角．要结合图形，熟记同旁内角的位置特点．变式3-2．（2022秋·浙江温州·七年级统考期中）如图，1∠和2∠是（ ）A ．同位角B ．内错角C ．对顶角D ．同旁内角【答案】D【分析】利用同旁内角的定义解答．两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．【详解】解：∠1和∠2是同旁内角．故选：D ．【点睛】本题主要考查了同旁内角，解题时要注意：同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U”形．变式3-3．（2022秋·湖北孝感·七年级校联考阶段练习）如图，与∠3是同旁内角的是（ ）A ．∠2B ．∠3C ．∠4D ．∠5【答案】C【分析】根据同位角、内错角、同旁内角的定义逐个判断即可．【详解】解：A ．∠2与∠3是内错角，不是同旁内角，故本选项不符合题意；B ．∠3与∠3是同一个角，不是同旁内角，故本选项不符合题意；C ．∠4与∠3是同旁内角，故本选项符合题意；D ．∠5与∠3是同位角，不是同旁内角，故本选项不符合题意；故选：C ．【点睛】本题考查了同位角、内错角、同旁内角的定义等知识点，能正确识图是解此题的关键．考查题型四 同位角、内错角、同旁内角的综合判断典例4．（2022秋·辽宁沈阳·七年级沈阳市南昌初级中学（沈阳市第二十三中学）阶段练习）如图，下列说法中错误的是（ ）A ．3∠和5∠是同位角B ．4∠和5∠是同旁内角C ．2∠和4∠是对顶角D ．2∠和5∠是内错角【答案】D【分析】根据同位角，同旁内角，对顶角以及内错角的定义进行判断．【详解】解：A ．3∠和5∠是同位角，正确，不符合题意；B ．4∠和5∠是同旁内角，正确，不符合题意；C ．2∠和4∠是对顶角，正确，不符合题意；D ．2∠和5∠不是内错角，错误，符合题意．故选D ．【点睛】考查了同位角、内错角、同旁内角以及对顶角．解答此类题确定三线八角是关键，可直接从截线入手．变式4-1．（2022春·河北邯郸·八年级校考开学考试）如图，下列判断正确的是（ ）A ．3∠与6∠是同旁内角B ．2∠与4∠是同位角C ．1∠与6∠是对顶角D ．5∠与3∠是内错角【答案】A【分析】根据同位角、同旁内角、内错角和对顶角的概念解答即可．【详解】解：A 、3∠与6∠是同旁内角，故本选项符合题意；B 、2∠与4∠不是同位角，故本选项不合题意；C 、1∠与6∠不是对顶角，故本选项不合题意；D 、5∠与3∠不是内错角，故本选项不合题意；故选：A ．【点睛】本题考查了同位角、内错角、同旁内角的定义，两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线(截线)的同旁，则这样一对角叫做同位角；两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线(截线)的同旁，则这样一对角叫做同旁内角；两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线(截线)的两旁，则这样一对角叫做内错角．变式4-2．（2022秋·浙江杭州·七年级校考期中）如图所示，下列说法中，错误的是（ ）A ．∠3与∠B 是同旁内角 B ．∠A 与∠1是同位角C ．∠2与∠3是内错角D ．∠1与∠B 是同位角【答案】D【分析】根据两线被第三线所截，同旁内角，内错角和同位角的定义进行判断即可．【详解】解：A 、∠3与∠B 是同旁内角，选项正确，不符合题意；B 、∠A 与∠1是同位角，选项正确，不符合题意；C 、∠2与∠3是内错角，选项正确，不符合题意；D 、∠1与∠B 不是同位角，选项错误，符合题意；故选D ．【点睛】本题考查三线八角，在找角的时候，首先要确定截线，然后根据它们之间的位置关系进行确定． 变式4-3．（2022秋·陕西渭南·七年级统考阶段练习）如图，下列说法错误的是（ ）A．∠1与∠2是同旁内角B．∠3与∠5是同位角C．∠1与∠4是内错角D．∠5与∠6是内错角【答案】C【分析】根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角分别进行分析可得答案．【详解】解：A、∠1与∠2是同旁内角，原题说法正确，不符合题意；B、∠3与∠5是同位角，原题说法正确，不符合题意；C、∠1与∠4不是内错角，原题说法错误，符合题意；D、∠5与∠6是内错角，原题说法正确，不符合题意；故选：C．【点睛】此题主要考查了三线八角，关键是掌握同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．。