1 平面机构组成
- 格式:doc
- 大小:32.50 KB
- 文档页数:3

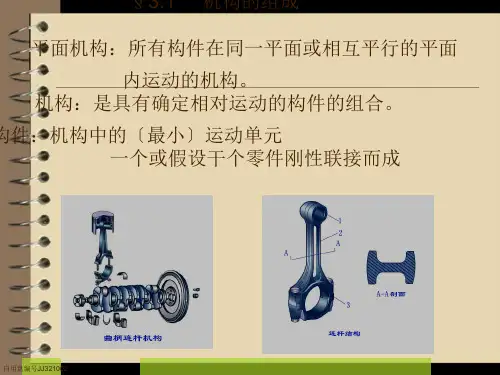






机械原理教案平面机构的组成原理分析 1.平面机构的组成原理任何机构中都包含原动件、机架和从动件系统三部分。
由于机架的自由度为零,每个原动件的自由度为1,而机构的自由度等于原动件数,所以,从动件系统的自由度必然为零。
杆组:自由度为零的从动件系统。
基本杆组:不可再分的自由度为零的构件组合称为基本杆组,简称基本组。
杆组的结构式为:l p n 23机构的组成原理:把若干个自由度为零的基本杆组依次联接到原动件和机架上,就可组成新的机构,其自由度数目与原动件的数目相等。
在进行新机械方案设计时,可以按设计要求根据机构的组成原理,创新设计新机构。
在设计中必须遵循的原则:在满足相同工作要求的前提下,机构的结构越简单、杆组的级别越低、构件数和运动副的数目越少越好。
2.平面机构的结构分析对已有机构或已设计完的机构进行运动分析和力分析时,首先需要对机构进行结构分析,即将机构分解为基本杆组、原动件和机架,结构分析的过程与由杆组依次组成机构的过程正好相反。
通常称此过程为拆杆组。
拆杆组时应遵循的原则:从传动关系离原动件最远的部分开始试拆;每拆除一个杆组后,机构的剩余部分仍应是一个完整的机构;试拆时,按二级组试拆,若无法拆除,再试拆高一级别的杆组。
3.平面机构的高副低代法目的:为了使平面低副机构结构分析和运动分析的方法适用于含有高副的平面机构。
概念:用低副代替高副方法:用含两个低副的虚拟构件代替高副 高副低代必须满足的条件: 1.替代前后机构自由度不变 2.替代瞬时速度加速度不变对于一般的高副机构,在不同位置有不同的瞬时替代机构。
经高副低代后的平面机构,可视为平面低副机构。
第三章平面机构的运动分析和力分析基本要求:1.掌握速度瞬心的概念,平面机构速度瞬心的数目及确定方法,学会用速度瞬心法对现有机构进行速度分析;2.掌握用相对运动图解法对机构进行速度分析的方法;3.掌握机构运动分析的复数矢量法,了解矩陈法;4.掌握平面机构力分析中的动态静力分析法,能够对给出机构用解析法建模并进行机构运动分析和力分析。



---------------------------------------------------------------最新资料推荐------------------------------------------------------
1 平面机构组成
思考题 1、构件和零件区别是什么?试分别举例说明两者的区别。
2、机器和机构有什么区别?试分别举例说明。
3、运动链和机构有何区别?具备什么条件运动链才具有运动的可能性?具备什么条件后才具有运动确定性?具备什么条件运动链才能成为机构?
4、何谓运动副?两构件之间具备什么条件才能形成运动副?
5、何谓机构运动简图?它着重表示机构的什么特点?能否用它来进行机构运动分析及动力分析?它与机构运动示意图有什么区别?
6、绘制机构运动简图应注意哪些事项?
7、计算机构自由度时应注意哪些事项?
8、学习机构进行组成和结构分析的目的是什么?
9、什么叫杆组?满足什么条件才能组成杆组? 10、何谓机构的级别? 11、请设计一个自由度为 2 的机构,并标明原动件。
12、高副低代的目的、原则及方法是什么? 13、如思考题图 1 所示,由全移动副组成的机构,请问该机构能否用平面机构自由度计算公式( 1)计算该机构自由度?应如何正确计算该机构的自由度?习题 1 将习题图 1 所示的各机构结构图绘制成机构运动简图,标出原动件和机架,并计算出各机构自由度。
图中 a)为内燃机主体机构; b)为唧筒机构; c)为链纫机脚踏板驱动机构; d)为缝纫机针往复运动机构; e)为表面粗
1/ 3
糙度测量仪; f)为手握式打气筒机构。
(注:
若结构图为立体图,按图无法量取尺寸时,允许只画出机构运动示意图)。
a) b) c) 12344132BAC4321思考题图 1 d) e) f)习题图 1 2 如习题图 2 所示,计算各机构的自由度。
指出机构中是否含有复合铰链、局部自由度及虚约束,说明计算机构自由度时应作如何处理。
指出该图中各机构欲作确定运动时机构应满足的条件。
图中 a)为控制气门运动的机构; b)为缝纫机送布运动机构;c)为锯料机机构; d)为铲土机机构; e)为仪表指示机构。
a) b) c) d)e)习题图 2 3 计算习题图 3 所示各机构的自由度,图中若有高副,请将其高副低代,再对该机构的组成进行分析,分析其由那些基本杆组组成,指出杆组级别及机构级别,指出机构原动件及机架。
4321OB’BAB’4BC123CAB1423小齿条齿条12347ABCDEFGG’6BCDE2134F’FP1P2ABCDEFGHIJF123456789556ABCD EF123412345ABCDEF67 a) b)c)习题图 3 4 确定习题图 4 所示 SOC 的方位特征矩阵及其运动输出特性分析设拓扑结构的符号表示为:
---------------------------------------------------------------最新资料推荐------------------------------------------------------ {}21//PRSOC 并选定末端运动副轴线上的点 o 为基点, 如习题图4 所示,将运动副的方位特征矩阵依次代入式( 26),请写出方位特征方程;进行转动元素之间的运算、平移元素之间的运算和运动输出特性分析。
习题图 4 5 确定习题图 5 所示 SOC 的方位特征矩阵及其特性分析设拓扑结构的符号表示为:
{}12SOCPP ,并选定末端运动副轴线上的点 o 为基点, 如习题图 5 所示,将运动副的方位特征矩阵依次代入式( 26),请写出方位特征方程;进行转动元素之间的运算、平移元素之间的运算和运动输出特性分析。
习题图 5 {} PPSOC 习题图6 {}),,(321PPPSOC 6 确定习题图 6 所示 SOC 的方位特征矩阵及其运动输出特性分析设拓扑结构的符号表示:
{} ),,(321PPPSOC,并选定末端运动副轴线上的点 o 为基点, 如习题图 6 所示,将运动副的方位特征矩阵依次代入式( 25),请写出方位特征方程;进行转动元素之间的运算、平移元素之间的运算和运动输出特性分析。
ABCDEFG12345678ABCDEF1234曲率中心ABCDEFPB12345
3/ 3。