耦合电感的计算
- 格式:ppt
- 大小:992.00 KB
- 文档页数:85


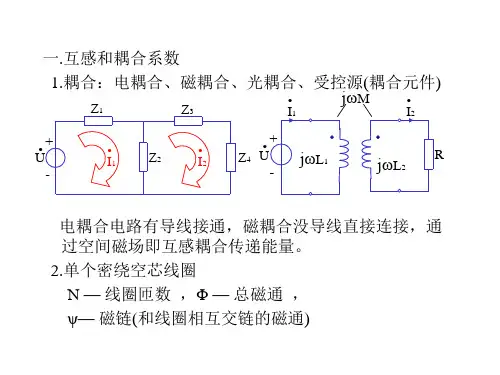
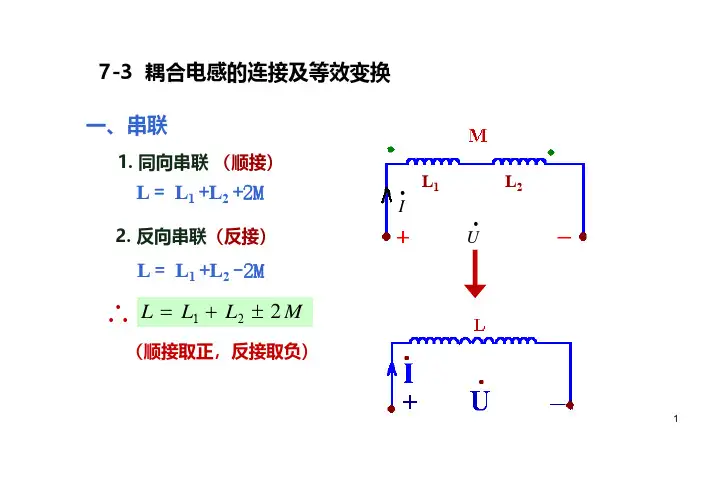

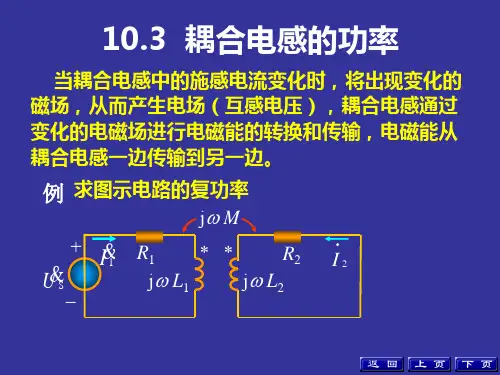

耦合电路电感功率计算公式在电路中,电感是一种重要的元件,它具有存储能量的特性,因此在电路中起着非常重要的作用。
对于耦合电路中的电感,我们常常需要计算其功率,以便更好地设计和分析电路。
本文将介绍耦合电路中电感功率的计算公式,并对其进行详细的解析。
在耦合电路中,电感功率的计算公式为:P = I^2 R。
其中,P表示电感功率,单位为瓦特(W);I表示电感中的电流,单位为安培(A);R表示电感的电阻,单位为欧姆(Ω)。
在实际的电路中,电感的电阻通常是非常小的,可以忽略不计。
因此,电感功率的计算公式可以简化为:P = I^2 0。
即电感功率为零。
这是因为电感本身并不消耗能量,它只是存储能量,并且会将能量释放回电路中。
因此,电感功率主要体现在能量的传输和转换过程中,而不是消耗能量的过程中。
然而,在一些特殊情况下,电感的电阻是不能忽略的,这时就需要考虑电感功率的计算。
例如,在高频电路中,电感的电阻会对电路产生一定的影响,因此需要对电感功率进行计算和分析。
在实际的电路设计和分析中,电感功率的计算通常是与电感的电流密切相关的。
因此,我们需要首先计算电感中的电流,然后再根据电流来计算电感功率。
电感中的电流可以通过欧姆定律来计算,即:I = V / Z。
其中,I表示电感中的电流,单位为安培(A);V表示电感两端的电压,单位为伏特(V);Z表示电感的阻抗,单位为欧姆(Ω)。
在耦合电路中,电感的阻抗可以通过以下公式来计算:Z = 2 π f L。
其中,Z表示电感的阻抗,单位为欧姆(Ω);π表示圆周率,约为 3.14159;f表示电路中的频率,单位为赫兹(Hz);L表示电感的电感,单位为亨利(H)。
将电感的阻抗代入电流公式中,就可以得到电感中的电流。
然后再根据电流来计算电感功率,即可得到最终的结果。
总之,耦合电路中电感功率的计算公式为P = I^2 R,其中I表示电感中的电流,R表示电感的电阻。
在实际的电路设计和分析中,通常需要根据电感的阻抗来计算电流,然后再根据电流来计算电感功率。
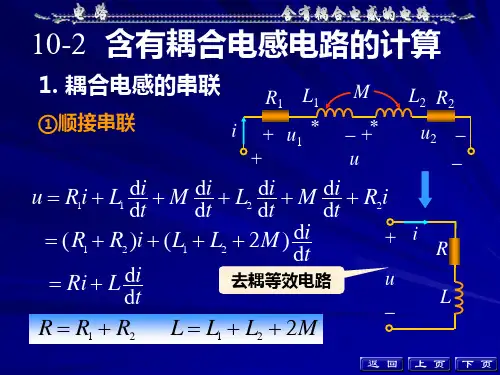



耦合变压器等效电感计算公式
耦合变压器是一种常见的变压器类型,其在电力系统中被广泛应用。
在设计和分析耦合变压器时,常常需要计算其等效电感。
等效电感是指变压器的主要部分(主绕组和副绕组)之间的互感作用所导致的电感值。
耦合变压器的等效电感可以通过以下公式计算:
L_eq = L_m + (k * sqrt(L_1 * L_2))
其中,L_eq是耦合变压器的等效电感,L_m是耦合变压器的互感电感,k是耦合系数,L_1和L_2分别是主绕组和副绕组的自感电感。
耦合变压器的互感电感可以通过以下公式计算:
L_m = (μ * N_1 * N_2 * A_c) / l_m
其中,L_m是互感电感,μ是磁导率,N_1和N_2分别是主绕组和副绕组的匝数,A_c是磁路截面积,l_m是磁路长度。
耦合系数k可以通过以下公式计算:
k = (L_m / sqrt(L_1 * L_2))
耦合变压器的自感电感可以通过以下公式计算:
L_self = (μ * N^2 * A_w) / l_w
其中,L_self是自感电感,N是绕组的匝数,A_w是绕组的截面积,l_w是绕组的长度。
这些公式可以用于计算耦合变压器的等效电感,从而帮助设计和分析电力系统中的耦合变压器。
电感耦合系数k导言电感耦合是一种常见的电磁现象,它在许多领域中都有广泛的应用。
电感耦合系数k是描述电感耦合效应强弱的一个重要指标。
本文将全面介绍电感耦合系数k的概念、计算方法和影响因素。
什么是电感耦合系数k电感耦合系数k是指两个电感线圈之间的耦合程度。
当两个电感线圈之间有磁场交流耦合时,它们之间会产生感应电动势,进而产生电流。
电感耦合系数k可以衡量这种耦合效应的强弱。
当k=1时,表示两个线圈完全磁场耦合;当k=0时,表示两个线圈之间没有磁场耦合。
电感耦合系数k的计算方法电感耦合系数k可以通过以下公式来计算:k = M / √(L1 * L2)其中,M为两个线圈之间的互感,L1和L2分别为两个线圈的自感。
通常情况下,线圈的自感可以通过测量线圈的电感值获得。
而线圈的互感可以通过将两个线圈串联后测量得到。
电感耦合系数k的影响因素电感耦合系数k受以下几个因素的影响:1. 线圈的几何结构线圈的形状、大小和排列方式等几何结构参数会影响电感耦合系数k的数值。
一般来说,线圈间距越小、线圈绕匝越多,电感耦合系数k越大。
2. 材料的特性线圈和介质材料的特性也会对电感耦合系数k产生影响。
对于磁性材料,其导磁率的数值越大,电感耦合系数k越大。
3. 工作频率工作频率对电感耦合系数k也有一定的影响。
在高频率下,电感耦合系数k通常会下降。
4. 线圈之间的距离两个线圈的距离也会对电感耦合系数k产生影响。
当线圈间的距离较小时,电感耦合系数k相对较大;而距离较远时,电感耦合系数k较小。
电感耦合系数k的应用电感耦合系数k在许多领域都有广泛的应用,以下列举了几个常见的应用场景:1. 无线能量传输电感耦合技术可以用于无线能量传输系统中。
通过将能量发送线圈和能量接收线圈之间的电感耦合效应,可以实现无线能量传输。
2. 数据传输电感耦合也被广泛应用于数据传输中。
例如,近场通信(NFC)技术中的非接触式支付,就利用了电感耦合技术。
3. 传感器设计电感耦合技术在传感器设计中也有应用。
耦合电感并联等效电感公式推导在电路中,两个电感器件并联时,会产生耦合效应。
耦合电感是指并联电感器件之间相互感应,通过互感的增减,对其等效电感值的影响。
为了推导耦合电感的并联等效电感公式,我们可以考虑以下电路图示。
图中的L1和L2为两个并联的电感器件,它们之间存在磁耦合。
我们假设这两个电感器件为线圈绕组,而且互相之间有一定的耦合系数k。
电感绕组上的电压与电流的关系可以表示为:V1 = L1 * di1/dtV2 = L2 * di2/dt通过Faraday定律我们可以得到:V1 = M * di2/dtV2 = M * di1/dt其中M为两个线圈的互感系数。
根据之前的推导,我们已知L1和L2之间存在一定的耦合系数k,那么互感系数M可以表示为:M = sqrt(L1 * L2) * k根据电路分析的基本原理,我们可以得到独立电感器件的总电感值Lp和总电流Ip与其分别对应的电感器件的电感值以及电流的关系为:Vp = Lp * dIp/dt其中Vp为总电压值。
我们可以将电流Ip分解为i1和i2两部分,即Ip=i1+i2、那么总电感值Lp可以表示为:Vp = (L1 * dIp/dt) + (L2 * dIp/dt)将dIp/dt替换为di1/dt + di2/dt,我们可以得到:Vp = (L1 + L2) * (di1/dt + di2/dt)这时我们可以将Lp替换为Li(即耦合电感的等效电感值),得到:Vp = Li * (di1/dt + di2/dt)根据之前的推导,Vp也可以表示为:Vp = M * (di1/dt + di2/dt)将M替换为sqrt(L1 * L2) * k,我们可以得到:Li * (di1/dt + di2/dt) = sqrt(L1 * L2) * k * (di1/dt +di2/dt)将等式两边除以di1/dt + di2/dt,我们可以得到:Li = sqrt(L1 * L2) * k这个公式即为耦合电感的并联等效电感公式。