下载文档原格式
第二章随机信号分析随机信号分析确定性信号分析的不同与联系：随机信号分析、确定性信号分析的不同与联系：随机信号分析的主要内容：随机过程的一般表述平稳随机过程高斯过程窄带随机过程正弦波加窄带高斯过程稳随机过过线性系平稳随机过程通过线性系统2010-9-271引言信号：一般是时间的函数确定信号：可以用确定的时间函数表示的信号 周期信号和非周期信号能量信号和功率信号基带信号和频带信号模拟信号和数字信号随机信号：具有随机性，可用统计规律来描述 通信过程中要发送的信号是不可预知的，因此具有随机性，是随机信号，但信号的统计特性具有规律性。
噪声和干扰是随机的信号噪声和干扰是随机的信号；无线信道特性（可理解为系统传递函数）也是随机变2010-9-272化的。
随机过程：与时间有关的函数，但任一时刻的取值不确定(随机变量)随机过程可以看成对应不同随机试验的时间过程的集合。
如n(或无数）台性能完全的接收机输出的噪声波形，每个波形都是一个确定函数，为一个样本函数，各波形又各不相同。
也可看成一个接收机，不同实验输出不同的样本函数。
随机过程是所有样本函数的集合。
2010-9-2731随机过程的一般表述1 随机过程的般表述(1)样本函数：随机过程的具体实现样本空间所有实现构成的全体~()i x t )()t 样本空间：所有实现构成的全体所有样本函数及其统计特性构成了随机过程{}1~(),,),i S x x t =……~()t ξ2010-9-274随机过程是随机变量概念的延伸，即随机变量引入时间变量，成为随机过程。
每一个时刻，对应每个样本函数的取值{i(),,,,}{x(t),i=1,2,…,n}是一个随机变量。
固定时刻t1的随机变量计为ξ(t1)。
随机过程看作是在时间进程中处于不同时刻的随机变量的集合。
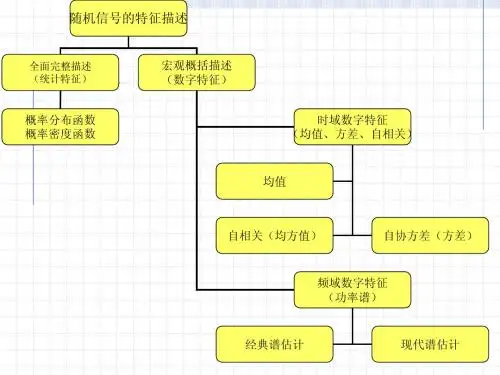
2010-9-27511随机过程的n维分布函数或概率密度函数往往不容易或不需要得到，常常用数字特征部分地表述随机过程的主要特征。
第二章 随机信号及其统计描述1．求在实数区间[]b a ,内均匀分布的随机变量X 均值和方差。
解： 变量X 的概率密度 ⎪⎪⎩⎪⎪⎨⎧≤≤-=其他，,01)(b x a a b x p均值 []⎰∞∞-+===2)(ba dx x xp X E m X方差 ⎰∞∞--=-=12)()()(222a b dx x p m x X Xσ2．设X 是具有概率密度函数)(x p 的随机变量，令x 的函数为0),exp(>-=a ax y试求随机变量y 的概率密度函数)(y p 。
解： 反函数0,ln 1>-=a y ax 雅可比式为 aydy dx J 1-==所以 0),ln 1(1)ln 1()(>-=-⋅=a y ap ay y a p J y p 4. 随机过程)(t X 为)sin()cos()(00t B t A t X ωω+=式中，0ω是常数，A 和B 是两个互相独立的高斯随机变量，而且0][][==B E A E ，222][][σ==B E A E 。
求)(t X 的均值和自相关函数。
7. 设有状态连续、时间离散的随机过程)2sin()(t t X Ω=π，式中t 只能取正整数，即 ,3,2,1=t ，而Ω为在区间)1,0(上均匀分布的随机变量，试讨论)(t X 的平稳性。
8.平稳随机过程)(t X 的自相关函数为1)10cos(22)(10++=-τττe R X ，求)(t X 均值、二阶原点矩和方差。
解： 可按公式求解[])()0(,)0()(,)(222∞-==∞=X X X X X X R R R t X E R m σ。
但在求解周期性分量时，不能得出)(∞R ，为此把自相关函数分成两部分： ()12)10cos(2)()()(1021++=+=-τττττeR R R X X X由于)10cos(2)(1ττ=X R 的对应的随机过程为 是随机变量为常数，ϕϕA t A t X ),10cos()(1+=所以[]0)(1=t X E而对于12)(102+=-ττe R X ，有1)(2=∞X R ，即[]1)(2±=t X E 所以[][][]1)()()(21±=+=t X E t X E t X E 可理解为1)(=∞X R从而有 []5)0()(2==X R t X E ，)()0(2∞-=X X X R R σ=4因此)(t X 的均值、二阶原点矩和方差分别为[]1)(±=t X E []5)(2=t X E 42=X σ9. 若随机过程)(t X 的自相关函数为)cos(21)(0τωτ=X R ，求)(t X 的功率谱密度。
