第八章 方差分析

同水平，
记A 为 1,A2,,Ar,B有 s个不同水B平 1,B2,， ,B记 s. 为
记在因素A的第 i个水平和因素B的第 j 个水平下的试验结果为：
x i(ji 1 ,2 , ,r,j 1 ,2 , ,s)
记 ＝ 1r s rsi1j1
i表 j 示总i平 .＝ 1 sj s均 1 i表 j 值示 ， A 的 因 i个 第 素水平.的
xijk＝＋ai＋bj abij ijk
r
i1
ai
0,
s
bj
j1
0
r
s
i1
(a
b)ij
0,
(a
j1
b)ij
0
i（ jk i 1,2,,r, j 1,2,,s,k1,2,,n)是相互独立，N且 (0,服2)从
其中 xij表 k，示 A 的 因i个 第 素水平 B 的 和 j个 第 因 水 素 k 平 次下 重 试验的n为 观重 测复 值试 ，验的次数。
(3)两因素之间的 可效 加应 的是 ，不 即因 在素 交之 互间 效存 应。
288 1092 278
113
816 149
--
例2：一名证券经纪人，收集了某年三个行业不同上市公司
的股票每股净收益资料，如下表.试比较这三种行业的公司的 每股净收益是否有显著的差异？如有差异，哪个行业每股净 收益最大？
表8.2 不同行业上市公司的每股净收益
ቤተ መጻሕፍቲ ባይዱ
行业类型
每股净收益
计算机
3.94 2.76 8.95 3.23 3.04 4.69 1.52 5.05
--
单因素方差分析中的一般假设: （1）随机变X量 j ~ N(j,2),j 1,2,k;
(2)各随机变量相互独立； （3）xij(i 1,2,,nj)是从Xj中抽取的简单随。 机样本 记ij xij j,称为随机误差。
故有 xi＝ j j＋i， j 此为单因素方差分析中的一般线性模型。
又可j将 分解为对因素 和 的对 总单 效个 应水a平 j，的效
医药
2.89 1.65 2.59 1.09 -1.07 2.30 -3.10
公用
-2.26 0.66 2.22 1.77 -0.15 2.10 2.89 1.12 -3.21 2.11
--
例8.3：某汽车销售商欲了解三种品牌的汽车X,Y,Z和四种标
号（A,B,C,D)的汽油对汽油消耗量的影响情况。在三种品牌 的汽车中随机抽出三辆，分别使用四种标号的汽油在同样的 公路上行使1小时，然后测量各自的消耗量，结果如下表。试 分析汽车的品牌和汽油的标号对汽油的消耗量有无显著影响？
即j＝＋aj。因xi此 ＝ j ＋ aj＋ -- ij.
从而单因素方差分析可归结为以下假设检验问题：
H0:a1a2ak 0,即因素对研究 著对 影象 响 H1:a1,a2,,ak不全0， 为即因素对研 显究 著对 影象
--
二、双因素方差分析模型
1.双因素无交互作用的方差分析模型及其假设条件
设某一研究对象受到两个因素A和B的影响，其中A有r 个不
(3)两因素之间的 加效 的应 ，是 即可 因素 在之 交间 互不 效存 应。
从而双因素无交互效应的方差分析可归结为以下假 设检验问题：
H0A:a1a2ar 0,即因A对 素研究对象无显 H0B:b1b2bs 0，即因 B对素 研究对象无 。显
--
2. 双因素有交互作用的方差分析模型及其假设：
模型可表示为：
好的商品随机地分配到四个条件相当的商店进行销售。1个月 后，各商店销售量如下表，试比较不同形式的包装对销售量 是否有显著影响？那一种包装效果最好？
表8.1 不同包装条件下商品销售量情况
包装 A
商店
Ⅰ
325
Ⅱ
154
Ⅲ
367
Ⅳ
144
B
617 331 819 407
C
D
E
229
856 319
181
553 167
第八章
方差分析与ANOVA过程
--
一.方差分析概述
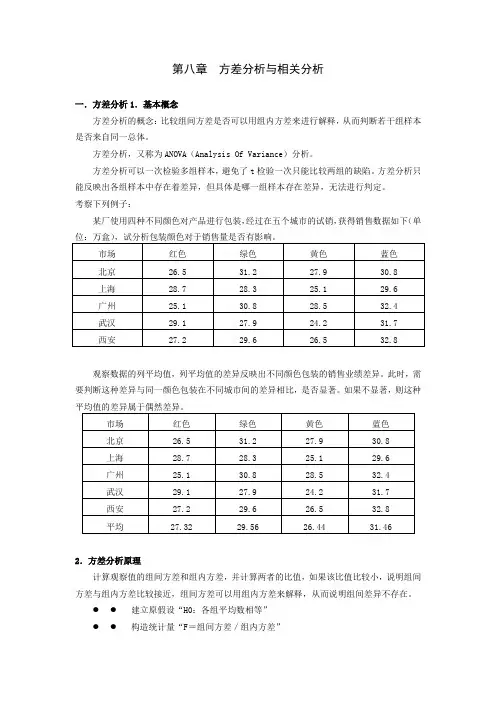
➢方差分析所要解决的问题： 方差分析主要用于解决当影响变量为定性变量，而 分析变量或称因变量为定量变量时，两个以上总体 均值相等的假设检验问题； 如果均值不完全相等，进一步比较各均值的大小。
--
例1：某公司为了研究五种形式的包装哪种更有效，把包装
涉及的因素为两个或两个以上的方差分析，统称为多因 素方差分析。
--
一、单因素方差分析模型
设因素X有k个水平，每个水平可视为一个小总体，分别用
X1,X2,,Xk来表示 Xj的 。总 记体均 j, 值为
则单因素方差分析即为如下假设检验问题：
H 0:12k,H 1:1,2,,k不全相等
设{xij}是从总 Xj中 体随机抽取的 为nj一 的个 样容 本量 ， xij表示j个 第水平i次 下观 第测i值 1,2, （ ,nj,j1,2,k)
--
该模型的一般假设:
（ 1 ） xij(i1,2,,r,j1,2,,s)可看作 A的 从 i个 第 因水 素平 B的 与 第 j个水平对 Xi中 j 应抽 的取 总 1的 体独 容立 量随 为机样
（ 2） r个 s 总体是相 且 Xij互 ~N(独 ij,2)立 i(1,的 2,,r， ,j1,2,,s);
(ab)ij表示因 A的 素第 i个水平 B的 ， -- 第 j个水平的共同效应。
该模型的一般假设:
（ 1） xij可 k 看作A的 从i个 第 因水 素平B的 与j个 第 因水 素平对 Xij应 中抽取的 n的容 独量 立为 随机样本；
（ 2） r个 s 总体是相 且 Xij互 ~N(独 ij,2)立 i(1,的 2,,r， ,j1,2,,s);
.j＝1r ir1ij表示因 B的 素第 j个水平的.平均值
--
双因素方差分析模型可表示为：
xij＝＋ai＋bj ij
r
s
ai 0, bj 0
i1
j1
ij是相互独立，且服N从(0, 2)
其中ai， ui. ,表示因 A的 素第 i个水平的效应； bj u.j ,表示因 B的 素第 j个水平的 . 效应
汽油 A
汽车
X
21.8
Y
31.3
Z
23.1
B
C
D
22.4 20.6 23.1 34.2 30.6 33. 7 27.3 26.1 28.6
--
➢方差分析模型及其假设条件
方差分析中，试验中要考察的指标称为试验指标， 影响试验指标的条件统称为因素或因子，而把因素 的取值称为处理或水平。
当涉及的因素只有一个时，称为单因素方差分析； 涉及的因素有两个时，称为双因素或两因素方差分析；