当前位置：文档之家 › 加减消元法说课稿 ppt课件

加减消元法说课稿 ppt课件

  • 格式：ppt
  • 大小：1.50 MB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

湘教版数学七年级上册3.6.2 加减消元法课件(共21张PPT)

湘教版数学七年级上册3.6.2 加减消元法课件(共21张PPT)
①×3，得 6x+9y=-33. ③③-②，得 (6x＋9y)-(6x-5y)=-33-9，
去括号，得 6x＋9y-6x+5y=-33-9，合并同类项，得 14y=-42,两边都除以14,得 y=-3.把y用-3代入方程①,得 2x＋3×(-3)=-11,解得 x=-1.因此，是原二元一次方程组的解. Nhomakorabea 议一议
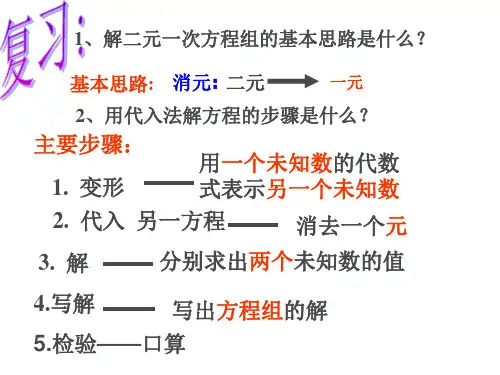
用自己的语言总结解二元一次方程组的基本思路，然后与同学交流.
解二元一次方程组的基本思路是： 消去一个未知数(简称消元)，得到一个一元一次方程,然后解这个一元一次方程,求出一个未知数的值,接着再去求另一个未知数的值. 代入消元法和加减消元法是两种求解方程组的方法,应根据具体情况灵活选择.
思 考
如果二元一次方程组中两个未知数的系数既不相等也不互为相反数，例如如何消去某个未知数，使其转化为一个一元一次方程？
观察方程①②,可发现方程①中x的系数的3倍等于方程②中x的系数,从而可利用等式的基本性质,先把方程①的左右两边都乘3,再将得到的方程与方程2左右两边对应相减,便得到关于y的一元一次方程. 下面采用上述方法来求解此方程组.
3.6.2 加减消元法
第3章 一次方程（组）
学习目标
1.了解解二元一次方程组的基本思想是消元；2.了解加减法是消元的方法； 3.会用加减法解二元一次方程组．（重、难点）4.会选择适当的方法解二元一次方程组．（重、难点）
新课导入
观 察
下面二元一次方程组中未知数y的系数有什么特点?这对解方程组有什么启发?
C
8.已知 和 都是方程y=ax+b的解，求a，b的值.
解析：根据题意得：①-②，得 4a=4,解得 a=1.把a=1代入②式，得 b=-2. 所以a=1， b=-2.

3.6.2 加减消元法 课件(共20张PPT) 湘教版七年级数学上册

3.6.2 加减消元法 课件(共20张PPT) 湘教版七年级数学上册

最终思想
将两个未知数变成一 个未知数求解---_消__元_
加减消元 变形→加减→求解→ 法的步骤 回__代__→写解→_检__验_
加减消元法 的解题技巧
方程组中同一个未知 数的系数的绝对值 _相__等_或_成__整__数__倍___
1. 用加减消元法解下列方程组：
(1) 3x 2y 8，
①
6x 5y 47；
y =_-_1__.
3.
已知
x
y
2，1是方程组mx x
y 3， 的解，求
ny 6
m
与
n
的值.
②
解：①×2得 6x + 4y = 16. ③
③ - ②得
9y = 63，
解得
y = 7.
把 y = 7 代入①得 3x + 2×7 = 8，
解得
x = -2.
因此原方程组的解是
x
－2
，
y
7.
(2) 3x 4y 11，
4x 5y 37；
① ②
解：①×4得 12x + 16y = 44. ③
①×3
6x+9y＝-33，③ 6x-5y＝9. ②
③-②
14y＝-42
2x+3y＝-11,① ①×5 6x-5y＝9. ② ②×3
10x+15y＝-55, ③ ③+④ 18x-15y＝27. ④
28x＝-28
例2 解二元一次方程组：
2x＋3y＝－11， 6x－5y＝9.
解：①×3 得
6x＋9y＝－33 ③
练一练 1.解方程： 3x + 5y = 21， ①
2x – 5y = -11. ②

(加减消元法)-PPT课件

(加减消元法)-PPT课件

1 、用加减法如何解下面的方程组:
2x+5y＝1 3x+2y＝7
2、思考题： 在解二元一次方程组中, 代入 法和加减法有什么异同点?
所以原方程组的解是
x＝5
y＝0
练一练：
用加减法解方程组：
3a+2b=7 2x-5y=-3 6a-2b=11 4x+y = 5
特点: 同一个未知数的系数相同或互为相反数
基本思路: 加减消元: 二元
一元
主步骤要：步骤：加减 求解
消去一个元 分别求出两个未知数的值
写解
写出原方程组的解
作业：
课本 P-98 3 (1)(2) 选做题 ： P-98 5
一.填空题：
x+3y=17
1.已知方程组
两个方程
2x-3y=6
只要两边
就可以消去未知数
2.已知方程组 只要两边
25x-7y=16 两个方程
25x+6y=10
就可以消去未知数
二.选择题
6x+7y=-19①
1. 用加减法解方程组
应用（ ）
6x-5y=17②
A.①-②消去y B.①-②消去x
C. ②- ①消去常数项 D. 以上都不对
3x+2y=13
2.方程组
消去y后所得的方程是（ ）
3x-2y=5
A.6x=8 B.6x=18 C.6x=5 D.x=18
• 讲例:
讲例: 用加减法解方程组:
5x +2y = 25 ①
3x +4y =15 ②
解：①× 2 - ②得+ 4y ＝15 解得： y＝0
解:由①+②得: 4x=48 由①-②得: 2y＝8

加减消元法公开课ppt课件

加减消元法公开课ppt课件

解这个方程，得 y 3
7
x 2
所以原方程组的解是
y
3 7
小结： 用加减法解二元一次方程组主要步骤有：
（1）观察
（2）加、减 （3）求解
（4）回代 （5）写解
同一个未知数的系 数相同或互为相反数 消去一个未知数（元）
求出一个未知数的值 求出另一个未知数的值
写出原方程组的解
一.填空题 1.已知方程组
像上面这种解二元一次方程组的方 法,叫做加减消元法,简称加减法。
口诀：同减异加
2x y 40 ①
例1：解方程组 x
y 22 ②
根据y的系数特点， 你能消去未知数ｙ吗？
解：① - ② ，得 x=18
将 x 18 代入② ，得
18 y 22
①- ②得 分析
2x +y = 40
-） x +y = 22
1、解二元一次方程组的基本思路是什么？
基本思路: 消元: 二元
一元
2、用代入法解方程的步骤是什么？
主要步骤： 1. 变形
用一个未知数的代数 式表示另一个未知数
2. 代入 另一方程
消去一个元
3. 解
分别求出两个未知数的值
4.写解
写出方程组的解
5.检验——口算
用代入法解下面的二元一次方程组呢？
3x 5y 41 ①
x+3y=17
两个方程只要两边 2x-3y=6
分别相加 就可以消去未知数 y ,得 3x=23 .
25x-7y=16
2.已知方程组
两个方程只要两边
分别相减
25x+6y=10 就可以消去未知数
x
,得13y=-6
.

加减消元法PPT教学课件

加减消元法PPT教学课件
D．苯不能使溴的四氯化碳溶液褪色，说明苯分子 中没有与乙烯分子中类似的碳碳双键
【解析】 乙酸属于一元羧酸，酸性强于碳酸， 所以可与NaHCO3溶液反应生成CO2，A正确；油 脂是高级脂肪酸的甘油酯，属于酯类，但不属于 高分子化合物，选项B不正确；甲烷和氯气反应 生成一氯甲烷，以及苯和硝酸反应生成硝基苯的 反应都属于取代反应，C正确；只有分子中含有 碳碳双键就可以与溴的四氯化碳溶液发生加成反 应，从而使之褪色，D正确。
【答案】 向其中加入足量的酸性高锰酸 钾溶液或溴的四氯化碳溶液，充分振荡，若 酸性高锰酸钾溶液或溴的四氯化碳溶液褪构
色，则说明b分子中含有 简式不能表示苯的结构。
，所以其结
【解析】
(1)a式结构中6个碳原子是对称的，只 有1种化学环境的氢原子，其一氯代 物和苯一样都只有1种，其二氯代物 和苯一样都有3种(如图)。 a式中只有碳碳单键，和溴的四氯化碳溶液、氢气 均不能加成，而苯环结构中存在介于碳碳单键和碳 碳双键之间的独特的化学键，虽然不能与Br2加成， 但是可以和氢气加成。
A. 2
B. 3
C. 4
D. 6
【解析】硼氮苯与苯结构类似，取代相邻两原子的
二氯代物只有1种，取代间位两原子的二氯代物有2
种，取代对位两原子的二氯代物有1种，共有4种。
2. 下列各组有机物中，只需加入溴水就能一一鉴 别的是( A ) A．己烯、苯、四氯化碳 B．苯、己炔、己烯 C．己烷、苯、环己烷 D．甲苯、己烷、己烯
2.加减法的基本思想：消元。 3.加减法解二元一次方程组主要步骤：
一变形，二加减，三消元，四求解， 五代入，六总结
拓展提升：
甲，乙两人同时解方程组mmxx
ny ny
8 ① 5②
由于甲看错了①中的m，解得

加减消元法说课稿课件

加减消元法说课稿课件

加减消元法的优缺点分析
优点
加减消元法是一种简单易懂的线性方 程组求解方法，适合初学者学习。其 计算过程直观，易于掌握。
缺点
加减消元法对于系数较大或较为复杂 的线性方程组可能计算量大，容易出 错。同时，对于无解或无穷多解的情 况处理不够灵活。
加减消元法在实际应用中的前景展望
线性方程组在实际问题中应用广泛，如工程、经济、科学等领域。加减 消元法作为一种基础且重要的求解方法，仍将在实际应用中发挥重要作 用。
方程等。
求解未知数
在化简方程组后，就可以通过解方程来求解未知数。
解方程的方法包括代入法、消元法和公式法等，具体方法应根据方程的实际情况选 择。
在求解未知数时需要注意解的合理性，确保解是符合实际情况的。
04 加减消元法的实例解析
实例一：简单线性方程组
总结词：基础应用
详细描述：加减消元法最常用于解决简单线性方程组，通过消元和代入法，将多 元一次方程组转化为单一方程，便于求解。
实例二：非线性方程组
总结词：扩展应用
详细描述：对于非线性方程组，加减消元法同样适用。通过消元过程，可以将非线性方程组转化为线性方程组，再利用代入 法求解。
实例三：实际应用问题
总结词：实际应用
详细描述：加减消元法在实际应用中具有广泛的应用价值，如经济、工程、物理等领域中的各种问题 ，可以通过建立数学模型并运用加减消元法求解。
加减消元法说课稿课件
目录
• 课程导入 • 加减消元法概述 • 加减消元法的基本步骤 • 加减消元法的实例解析 • 课程总结与展望 • 作业与思考题
01 课程导入
课程背景
当前数学教育的发展趋势
随着教育改革的深入，数学教育越来越注重培养学生的实际 应用能力和创新思维。加减消元法作为代数中的基础内容， 对于培养学生的逻辑思维和问题解决能力具有重要意义。

人教版加减消元法ppt导学课件

人教版加减消元法ppt导学课件
y 4.
知1－导
思考： 联系上面的解法，想一想怎样解方程组 3x 10y 2.8, 15x 10y 8.
知1－导
从上面两个方程组的解法可以看出：当二元一 次方程组的两个方程中同一未知数的系数相反或相 等时，把这两个方程的两边分别相加或相减，就能 消去这个未知数，得到一个一元一次方程. 这种方 法叫做加减消元法，简称加减法 (addition-subtraction method).
人教版..加减消元法实用课件（PPT优 秀课件 ）
人教版..加减消元法实用课件（PPT优 秀课件 ）
知3－讲
例5 解方程组： 2x 3y 3,
①
3x 2y 11.
②
导引：方程①和②中x，y的系数的绝对值都不相等，
也不成倍数关系，应取系数的绝对值的最小
公倍数6，可以先消去x，也可以先消去y.
人教版..加减消元法实用课件（PPT优 秀课件 ）
②-①，得11x=4.4.
① ②
解这个方程，得x=0.4.
人教版..加减消元法实用课件（PPT优 秀课件 ）
人教版..加减消元法实用课件（PPT优 秀课件 ）
知3－讲
把x=0.4代入①，得y=0.2. 因此，这个方程组的解是 x 0.4,
y 0.2. 答：1台大收割机和1台小收割机每小时各收割小
麦0. 4 hm2和0. 2 hm2 上面
2x 5y 11
y 3.
知识点 1 直接加减消元
知1－导
思考：
前面我们用代入法求出了方程组
x y 10, ① 2x y 16. ②
的解. 这个方程组的两个方程中，y的系数有什么关
系？利用这种关系你能发现新的消元方法吗？
知1－导

课件)122加减消元法(一)课件

课件)122加减消元法(一)课件

加减消元法的原理
原理
加减消元法的原理是通过添加或减去 方程中的某些项，使得某一未知数的 系数变为零，从而将多元一次方程组 转化为一元一次方程。
转化过程
通过加减消元法，可以将多元一次方 程组转化为简单的一元一次方程，从 而方便求解。
加减消元法的应用场景
线性方程组
加减消元法适用于解线性方程组，特别是当方程个数大于未知数个数时，可以 通过加减消元法求解。
实例三：实际应用问题
总结词：通过实际应用问题展示加减消元法的 应用。
01
选取一个实际问题，如路程问题、购物问 题等。
03
02
详细描述
04
将实际问题转化为二元一次方程组。
通过加减消元法求解该方程组，得到实际 问题的解。
05
06
对解进行解释和验证，确保其符合实际情 况。
05
CHAPTER
总结与回顾
本节课的重点和难点
重点
掌握加减消元法的原理和步骤，能够运用该方法解决线性方 程组问题。
难点
理解加减消元法的数学逻辑，以及如何选择合适的消元步骤 以简化方程组。
下节课预告
介绍加减消元法的进阶应用，如 处理多个方程组和特殊情况的处
理。
通过实例演示如何运用加减消元 法解决实际问题。
讲解如何利用编程语言实现加减 消元法，并分享相关的代码实现。
06
CHAPTER
习题与作业
基础习题
总结词：掌握加减消元法的基
本原理和步骤
01
详细描述
2+3=5
3+4=7
04
1+2=3
02
05
5+6=11
03 06

加减消元法(第课时)PPT课件

加减消元法(第课时)PPT课件
3
a

2
b

8
，②

3
分析：方法一：直接解方程组，求出 a 与 b 的值，然后就
可以求出 a + b.
方法二：① + ② 得 4a + 4b = 12，
故a + b = 3.
巩固练习
6.已知关于，的二元一次方程组
2 + 3 =
的解互为相反数，
+ 2 = −1
求的值。
解：
2 + 3 =
6x - 5y = 17
②
A. ① - ② 消去 y
B. ① - ② 消去 x
C. ② - ① 消去常数项
D. 以上都不对
应用（ B）
巩固练习
3.已知
+ = 7
=2
是二元一次方程组
的解，求 − 的值
=1
− = 1
解：把
=2
代入原方程组中可以得到：
=1
2 + = 7
解得
n＝7.
3m+2×7＝8，
m＝﹣2.
m=﹣2,
n=7.
（4）
2x－4y=34, ①
5x＋2y＝31； ②
把x＝8代入①式，得
解得
因此原方程组的解是
[选自教材P10 练习]
x＝8.
2×8－4y＝34，
9
y＝﹣2 .
x=8,
9
y=﹣2 .
巩固练习
2. 用加减法解方程组
6x + 7y = －19，①
找系数的最小公倍数
归纳总结
用加减法解二元一次方程组：
特点：同一个未知数的系数相同或互为相反数

二元一次方程组的解法加减消元ppt

二元一次方程组的解法加减消元ppt

02
加减消元法介绍
加减消元法的原理
原理概述
加减消元法是通过消元的方式，将二元一次方程组转化为一元一次方程，从 而求解出方程的解。
具体步骤
通过对二元一次方程组中两个方程进行线性组合，将其中一个未知数表示成 另一个未知数的函数形式，从而消去一个未知数，得到一个一元一次方程。
加减消元法的应用范围
适用范围
2023
二元一次方程组的解法加 减消元ppt
目录
• 引言 • 加减消元法介绍 • 加减消元法实例
01
引言
本节课的目的和背景
介绍二元一次方程组及其解法的概念和重要性 强调本节课的主要内容和教学目标
二元一次方程组及其解法简介
回顾一元一次方程和二元一次方程组的概念
简单介绍解二元一次方程组的基本思路和方法：加减消元法 和代入消元法
THANK YOU.
03
加减消元法实例
实例一：用加减消元法解二元一次方程组
总结词：有效步骤
详细描述：1.将方程组整理成标准形式；2.根据方程组系数特点，确定消元方案 ；3.通过加减消元，将未知数减少至一个；4.解出最后一个未知数。
实例二
总结词：注意问题
详细描述：1.观察方程组特点，确定消元方案；2.将参数作为 常数处理，进行加减消元；3.解出未知数；4.将参数代入方程 组验证解的正确性。
加减消元法适用于求解二元一次方程组，特别适用于系数较简单的方程组。
不适用范围
对于系数较大或较为复杂的方程组，加减消元法可能会因为计算量大而变得繁琐 ，需要使用其他方法进行求解。
加减消元法的注意事项
ห้องสมุดไป่ตู้
注意事项
在使用加减消元法时，需要注意系数是否为零的情况，以及 是否会出现增根的情况。

加减消元法说课稿课件

加减消元法说课稿课件

3 深究教材说教法
4 因材施教说学法
先学后教
当堂训练
自主探究
合作交流
5 综合设计说过程
共 计 一 节 课
3
1
导入新课 2’
2
探索规律 5’
任务实施 23’
4
当堂训练 15’
5.1 导入新课
（1）上节课利用了什么方法解二元一次方程组？（代入消元法） （2）解二元一次方程组的基本思想是什么？（消元）
导入新课这一环节设计的2个问题，目的是帮助学生回 忆上节课所学的主要知识和重要思想。
5.2 探索规律
认真看课本（P99练习下面—— P100） 想一想： 思考P99的例题中，“②－①”的作用是什么？ 看例3时，重点看第一步，理解“①×3，②×2”的目的是什么？ P100“思考”和 “云图”中的问题。
① ② ③ ④
解二元一次方程组的 一般步骤：
6 x 9 y 36
变形 加减 求解 写解
6 x 8 y 34
y2 2 x 3 2 12
2x 6 x3
所以方程组的解是
x 3 y 2
6 针对实效说反思
本节课的教学过程从新课标的要求出发，充分体现 了课堂上真正的主人是学生这个原则。整个课堂学生自 己发现问题、思考问题、解决问题和总结方法。从“当 堂训练”的效果来看本节课的教学目标完成较好。学生 基本掌握了用加减消元法解二元一次方程组。但是仍有 一些不足之处： 对于二元一次方程组中同一未知数系数的绝对值 不相等时的变形，有部分学生还是不熟练。 运用等式性质对方程组进行变形时，常数项忘记 同时乘以最小公倍数。 所以，这也提醒我在以后的教学上，不仅要重视新 知识的学习，同时也要重视对旧知的巩固练习。

加减消元法(第课时)同步PPT课件

加减消元法(第课时)同步PPT课件

解：解方程组
4
x
y
5,
得
3x 2 y 1
x 1， y 1
把 代x 入1 方程组
y 1
ax by 3,
ax解 b此y 方 1程，组得
所以 a2－2ab＋b2＝1.
a 2, b 1.
课堂练习
2、解方程组
2(x y) 3(x y) 30，① 2(x y) 3(x y) 6. ②
(1) 3x 2y 8，
①
6x 5y 47；
②
解：①×2得 6x + 4y = 16.③
③ y = 7 代入①得 3x + 2×7 = 8，
解得
x = -2.
因此原方程组的解是
x
－2
，
y
7.
巩固练习
(2) 2x 5y 24， ①
5x 2y 31.
3.代入法、加减法的基本思想是什么？ 消去一个未知数（简称为消元），得到一个一元一次方程， 然后解这个一元一次方程.
4.我们在解二元一次方程组时，该选取何种方法呢？
复习回顾
加减消元法的主要步骤. (1) 变形 使同一个未知数的系数相同或互为相反数 (2) 加减 消去一个元 (3) 求解 求出两个未知数的值 (4) 写解 写出方程组的解
新知探究
例 6 解二元一次方程： 3x＋4y=8, ①
4x＋3y=﹣1. ②
代入消元法
解：由①式可得 x 8－4 y . 3
③
于是可以把③代入②式，得
（5 8－4 y ）－3 y 1 ,
3
解得
y＝5.
将y=5代入③式 ，得 因此原方程组的解是
x=﹣4, y=5.
x＝﹣4.
新知探究

二元一次方程组的解法——加减消元法PPT课件(沪科版)

二元一次方程组的解法——加减消元法PPT课件(沪科版)

x＋3y＝4， (2)14x＋12y＝0. 解：化简原方程组得xx＋＋32yy＝＝40，.②①由①－②，得 y＝4， 把 y＝4 代入①，得 x＋12＝4，解得 x＝－8.所以xy＝＝4－. 8，
9．[月考·合肥四十二中]阅读下列解方程组的部分过程，回 答下列问题： 解方程组x3－ x－2y2＝y＝5，3.②① 现有两位同学的解法如下： 解法一：由①，得 x＝2y＋5，③ 把③代入②，得 3(2y＋5)－2y＝3.…… 解法二：①－②，得－2x＝2.……
第3章 一次方程与方程组
3.3 二元一次方程组及其解法 第4课时 二元一次方程组的解法——
加减消元法
提示：点击 进入习题
核心必知
1 绝对值
基础巩固练
答案显示
1 相等；互为相反数；加减
2 ①＋②；①－②
3 －1
4D
提示：点击 进入习题
答案显示
5A 7C
6 ② ×3 － ① ×5 ； ① ×3＋②×2 x＝－6， x＝－8，
x＝2， 14 y＝－1.
答案显示
素养核心练
15
x＝4， y＝32.
用加减消元法解二元一次方程组时，必须使这两个方 程中某一个未知数的系数的_绝__对__值___相同．
1．方程组22xx＋－34yy＝＝－5，2中 x 的系数特点是__相__等____ ; 方程组37xx－＋55yy＝＝82，中 y 的系数特点是_互__为__相__反__数___； 这两个方程组用___加__减_____消元法解比较简单．
8 (1)y＝6. (2)y＝4.
9 (1)代入消元法；加减消元法；基本思路都是消元(或都设 法消去了一个未知数，使二元问题转化为了一元问题)
x＝－1， (2)y＝－3.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课堂实录(2)
5.3.3 归纳总结
➢加减消元法的概念
➢用加减消元法解二元一次方程组的一般步骤
加深学生对本节知识的理解和记忆，培养他们归纳、 概括能力。
加减消元法说课稿
（一）必做题（5’+5’+20’=30分）
1.用加减消元法解方程组 2x 3y 3 时，有以下四种变形，正确的是（ ）
3x 2y 11
① ②
本题中x的系数相等，用减法消元
加减消元法说课稿
2x 3y 12
①
（3） 3x 4 y 17
②
本题中x、y的系数既不互为相反数，又不相等，所以 要先将原方程组变形，使同一个未知数的系数互为相 反数或者相等，再用加减法消元。
目的：既检测了学生通过自学对加减消元法的掌握程度， 同时也可以锻炼他们的语言表达能力。
加减消元法说课稿
自我检测
分组协作
归纳总结
学生按照老师提出的要求自主探究、合作学习。 对于问题，分组交流，相互补充。 教师参与小组讨论，解答疑问。
加减消元法说课稿
（1）
3x 7 y 9 4x 7 y 5
① ②
本题中y的系数互为相反数，用加法消元
（2）
3x 5y 5 3x 4y 23
A.
4x 6y 3 9x 6y 11
B.
6x 3y 9 6x 2y 22
C.
4x 6y 6 9x 6y 33
D.
6x 9y 3 6x 4y 11
课堂小结 2.已知
3x 2y 2x 3y
17 13
，则
xy
3.解下列方程组
2x 3y 12
(1) 3x 4y 17
课堂实录(1)
加减消元法说课稿
在教师引导下，学生分小组讨论，通过共同探究的方式来完成
➢ 第(1)、 (2)题分别是用什么方法消元的？为什么用这种 方法消元？ ➢第(3)题比(1)、(2) 题多了哪一步？为什么要多这一步？ ➢归纳用加减消元法解二元一次方程的一般步骤
目的：不仅让学生了解了加减消元法解方程组的过程，同时也提 高了学生从不同的角度观察和分析事物的能力。
② × 2，得： 6x8y34 ④
③-④,得: 将y=2代入①,得:
y2 2x3212
2x6 x 3
所以方程组的解是
x 3
y
2
解二元一次方程组的 一般步骤：
变形
加减 求解
写解
加减消元法说课稿
本节课的教学过程从新课标的要求出发，充分体现 了课堂上真正的主人是学生这个原则。整个课堂学生自 己发现问题、思考问题、解决问题和总结方法。从“当 堂训练”的效果来看本节课的教学目标完成较好。学生 基本掌握了用加减消元法解二元一次方程组。但是仍有 一些不足之处：
加减消元法说课稿
知识与技能
过程与方法
情感、态度 与价值观
➢ 会用加减消元 法解简单的二元 一次方程组
➢ 理解加减消元 法的基本思想， 体会化未知为已 知的化归思想
➢ 通过经历加减消 元法解方程组，体 会消元思想的运用， 经过引导、讨论和 交流理解用加减消 元法解二元一次方 程组的一般步骤
教学目标
➢ 通过交流、合 作、讨论获取成功 的体验，感受加减 消元法的应用价值， 同时体会数学与日 常生活的紧密联系， 认识到数学的价值
人教版七年级数学下册
解二元一次方程组——加减消元法
说课设计
加减消元法说课稿
1
教材分析
2
学情分析
3
教法分析
4
学法分析
5
教学过程
6
教学反思
精品资料
加减消元法说课稿
1.1 地位与作用
本节课内容节选自人教版七年级数学下册第八章 第二节第二课时。是在学生学习了代入消元法解二元 一次方程组的基础上，继续学习的另一种消元方法。 教材的编写目的是让学生通过学习加减消元法充分体 会“化未知为已知”的转化过程。理解并掌握解二元 一次方程组的基本方法，为以后函数等知识的学习打 下基础。
➢对于二元一次方程组中同一未知数系数的绝对值 不相等时的变形，有部分学生还是不熟练。 ➢运用等式性质对方程组进行变形时，常数项忘记 同时乘以最小公倍数。 所以，这也提醒我在以后的教学上，不仅要重视新 知识的学习，同时也要重视对旧知的巩固练习。
(2)
5
x
6 x
5 6
1 y
7
y
3 2Βιβλιοθήκη （二）选做题（10分）4.甲、乙两人同求方程 axby7的整数解，甲正确的求出一个解为
看成 axby1，求的另一个解
x y
1 ，求
2
a , b 的值。
x y
1 1
，乙把
axby7
（三）思考题（10分）
5.解方程组
200x4200y52003 200x5200y42006
➢先学后教 ➢当堂训练
4 因材施教说学法
➢自主探究 ➢合作交流
加减消元法说课稿
共
计
1 导入新课 2’
一
节
课
2 探索规律 5’
3 任务实施 23’ 4 当堂训练 15’
5.1 导入新课
（1）上节课利用了什么方法解二元一次方程组？（代入消元法） （2）解二元一次方程组的基本思想是什么？（消元）
导入新课这一环节设计的2个问题，目的是帮助学生回 忆上节课所学的主要知识和重要思想。
加减消元法说课稿
教学重点
教学难点
➢用加减消元法解 二元一次方程组
➢方程组中同一未知 数系数绝对值不相 等时的变形过程
加减消元法说课稿
从知识体系上来说，学生上学期已经学习了整 式的加减和解一元一次方程的方法。这学期通过代 入消元法的学习，对消元思想已经有了初步认识， 具备了学习本节课的必要条件。
3 深究教材说教法
5.2 探索规律
认真看课本（P99练习下面—— P100） 想一想： ➢思考P99的例题中，“②－①”的作用是什么？ ➢看例3时，重点看第一步，理解“①×3，②×2”的目的是什么？ ➢P100“思考”和 “云图”中的问题。
“探索规律”中设计的3个问题，目的是为学生在自学 本节课的知识点和把握重、难点内容时起引导作用。
“当堂测试”设有必做题、选做题和思考题共5 题。其中必做题 3道，选做题1道，思考题1道。 目的是满足不同层次的学生需求，体现分层教学。
加减消元法说课稿
8.2 解二元一次方程组——加减消元法
一、加减消元法的概念
二、例题及解题过程
2x 3y 12 ①
例1 3x 4y 17
②
解: ①× 3，得: 6x9y36 ③