当前位置：文档之家 › 高等数学 第八章 多元函数微分学

高等数学 第八章 多元函数微分学

  • 格式：ppt
  • 大小：1.42 MB
  • 文档页数：47

下载文档原格式

  / 47

合集下载

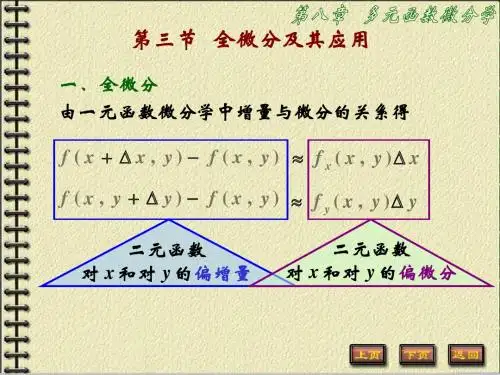
《高等数学B》第八章 多元函数微分学 第三节 全微分及其应用

《高等数学B》第八章 多元函数微分学 第三节 全微分及其应用
P ′( x + ∆ x , y + ∆ y ) ∈ P 的某个邻域
∆ z = A∆ x + B∆ y + o( ρ ) 总成立 ,
上式仍成立， 当 ∆ y = 0 时，上式仍成立，此时 ρ = | ∆ x | ,
f ( x + ∆ x , y ) − f ( x , y ) = A ⋅ ∆ x + o(| ∆ x |) ,
所求全微分 dz = e 2dx + 2e 2dy .
y yz 例2 计算函数 u = x + sin + e 的全微分 . 2
y ∂u 1 ∂u ∂u yz yz 解 = ye , =1, = cos + ze , ∂y 2 2 ∂z ∂x
所求全微分
1 y yz yz du = dx + ( cos + ze )dy + ye dz . 2 2
例4 试证函数
1 , ( x , y ) ≠ ( 0 , 0) , xy sin 2 2 x +y f ( x , y) = 0, ( x , y ) = ( 0 , 0) .
在点 (0 , 0) 连续且偏导数存在，但偏导数在点 (0 , 0) , 0) 可微 . 不连续， (证明略) 证明略)
∂u ∂u ∂u du = dx + dy + dz . ∂x ∂y ∂z
例1 计算函数 z = e x y在点 ( 2 , 1) 处的全微分 . 解
∂z = ye xy , ∂x
∂z = e2 , ∂x ( 2 , 1 )
∂z = xe xy , ∂y
∂z = 2e 2 , ∂y ( 2 , 1 )
∆ z ≈ dz = f x ( x , y )∆ x + f y ( x , y )∆ y .

高等数学 第八章 多元微分 第三节 全微分

高等数学 第八章 多元微分 第三节 全微分

∂z ∂z d z = ∆x + ∆y ∂x ∂y
注 1.习惯上,将自变量增量 ∆ x , ∆ y 分别记为 ， 分别记为dx 1.习惯上, 习惯上
∂z ∂z dy, 所以上式常记作： d z = 所以上式常记作： dx + dy ∂x ∂y
2. 定理 的逆定理不成立 . 定理1 偏导数存在,函数不一定可微! 即 偏导数存在,函数不一定可微!
上页 下页 返回 结束
证 由全增量公式
令∆y = 0, 得到对 x 的偏增量
x + ∆x
∴
= A∆x + o( ∆x ) ∂z ∆x z = lim =A ∂x ∆x→0 ∆x
x
∂z 同样可证 =B ∂y
因此有
上页 下页 返回 结束
反例
xy 2 2 x2 + y2 x + y ≠ 0 . f (x, y) = 2 2 0 x + y =0
ρ→0
∆x→0 ∆y→0
lim f ( x + ∆x, y + ∆y) = lim[ f ( x, y) + ∆z]
ρ→0
= f ( x, y)
故函数 在点 处连续. 处连续. ) z = f ( x, y
上页
下页
返回
结束
二、可微的条件
定理1 必要条件) 定理1(必要条件) 若函数 z = f (x, y) 在点 y) 可微 , 在点(x, 则函数在该点的偏导数 必存在, 必存在, 且有 证明
dz = d f = A∆x + B∆y
内各点都可微, 则称此函数在 内可微. 若函数在域 D 内各点都可微 则称此函数在D 内可微
上页

高等数学-第八章 多元函数微分学

高等数学-第八章 多元函数微分学

(ex ) e x
(loaxg)x
1 ln
a
(arcxs)in
1
1
x
2
(lnx) 1
x
(arccx)os 1
1 x2
(arcxt)an
1
1
x
2
(acrc ox)t
1
1 x
2
2. 求一点处偏导数的方法
• 利用定义: fx (x 0 ,y 0 ) lx 0 if( m x 0 x ,y 0 x ) f(x 0 ,y 0 )
第八章 多元函数微分学 知识总结
一. 多元函数的基本概念 二. 多元函数的偏导数、微分与方向导数 三. 多元函数微分法 四. 多元函数微分学的几何应用 五. 多元函数的极值和最值
一. 多元函数的基本概念
1. 区域 2. 多元函数概念
3. 多元函数的极限 4. 多元函数的连续性
1) 函数 f(P)在P0连续 P l iP 0 m f(P)f(P 0)
例.
设
f(x,y,z)xco y syco zs zco x,求 sdf 1co x s co y s co z s
(0,0,0) .
解: f(x,0,0) x 3cosx
fx(0,0,0)
x
3cosx
x0
1 4
利用轮换对称性 , 可得 fy(0,0,0)fz(0,0,0)1 4
d f( 0 ,0 ,0 ) f x ( 0 ,0 ,0 ) d x fy ( 0 ,0 ,0 ) d y f z ( 0 ,0 ,0 ) d z
(1) 检验函数是否连续,若不连续一定不可微
(2 )求 fx (x 0 ,y 0)、 fy (x 0 ,y 0) 注 ： 若 有 一 个 不 存 在 则 一 定 不 可 微

（完整版）高等数学（同济版）多元函数微分学练习题册.doc

（完整版）高等数学（同济版）多元函数微分学练习题册.doc

（完整版）高等数学（同济版）多元函数微分学练习题册.doc第八章多元函数微分法及其应用第一作一、填空：1. 函数 z ln(1 2 )y x23x y 的定义域为x12. 函数 f (x, y, z) arccosz的定义域为y 2x 23. 设 f ( x, y) x 2 y 2 , (x) cos x, ( x) sin x, 则f [ (x), (x)].sin xy .4. lim xx 0二、（）： 1. 函数1的所有断点是 :sin x sin y(A) x=y=2n π（ n=1,2,3,?）；(B) x=y=n π (n=1,2,3, ?) ； (C) x=y=m π (m=0, ±1，± 2，? )；(D) x=n π ,y=m π (n=0, ± 1，± 2，?，m=0,± 1,± 2,? )。

答：（）sin 2( x 2 y 2 , x 2y 22. 函数 f (x, y)x 2 y 2在点（ 0， 0）：2 ,x 2 y 2（ A ）无定；（B ）无极限；（ C ）有极限但不；（ D ）。

答：（）三、求 lim2xy 4 .x 0 xyya四、明极限 limx 2 y 22 不存在。

2 2xx y ( x y)y 0第二节作业一、填空题：1 sin( x2 y), xy 01. 设 f ( x, y)xy ,则 f x (0,1) .x 2 ,xy2. 设 f (x, y)x ( y 1) arcsinx, 则 f x ( x,1).y二、选择题（单选）：设 z 2x y 2 , 则 z y 等于 :( A) y 2 x y 2 ln 4; (B) (x y 2 ) 2 y ln 4; (C ) 2 y( x y 2 ) e x y 2 ;(D ) 2 y 4 x y 2 .答：（）三、试解下列各题：1. 设 z ln tan x , 求 z, z .2. 设 z arctan y, 求2z .y x yxx y四、验证 rx 2 y 2 z 2 满足2r2r2r 2 .x 2 y 2 z 2r第三节作业一、填空题：1. 函数 zy 当x 2, y时的全增量z全微分值x 1, x 0.1, y0.2dz.y2. 设z e x , 则dz.二、选择题（单选）：1. 函数 z=f(x,y) 在点 P 0（ x 0,y 0）两偏导数存在是函数在该点全微分存在的：（ A ）充分条件；（ B ）充要条件；（ C ）必要条件；（ D ）无关条件。

高等数学第八章多元微分第四节多元复合函数求导

高等数学第八章多元微分第四节多元复合函数求导

x yx y
上页 下页 返回 结束
上述求导规则称为多元复合函数的链式法则. 具有 如下特点:
1. 复合后的函数有几个自变量，对应地就有几个 偏导数;
2. 有几个中间变量，就有几项相加;
3. 相加的每一项都是复合函数对某一中间变量的
偏导数和该中间变量对特定自变量的偏导数的乘积;
4. 中间变量或自变量只有一个时，公式中的求导
记号用 d ，不止一个时用偏导数记号
dx
x
5
上页 下页 返回 结束
特例1. z f( u ,v ) ,u ( x ,y ) ,v ( y )
z z u z 0 z u x u x v u x
z z u z dv y u y v d y
特例2. z f( x ,v ) ,v ( x ,y )
2001考研
解 由题设 ( 1 ) f(1 ,f(1 ,1 ))f(1,1)1
d 3(x)
dx
x
132(x)ddx
x1
3 f1(x,f(x,x))
f 2 ( x , f ( x , x ) )
32 3(23)51
x 1
上页 下页 返回 结束
个人观点供参考，欢迎讨论！
续的偏导数, 则复合函数
的导数为
dzzduzdv dt u dt v dt
全导数 证略（利用全增量公式）
z
uv tt
注 求多元复合函数的偏导数，只要对每一个中间
变量施行一元函数的链式法则，再相加即可. 重要的是
搞清楚函数的复合关系.
上页 下页 返回 结束
推广 设 zf(u,v,w ),而
u ( t ) ,v ( t ) ,w ( t )
上页下页返回结束dtdzdtdzdtdudtdvcoslnsinlncosln上页下页返回结束解利用全导数求导数dxdydxdydxdudxdvcossinlnlnlnlnsin上页下页返回结束引入中间变量cossin上页下页返回结束1211上页下页返回结束xyzxyxyzxy上页下页返回结束二全微分形式的不变性是自变量还是中间变量则复合函数其全微分的表达形式都一样这一性质称为全微分形式的不变性

高等数学教材第八章

高等数学教材第八章

高等数学教材第八章第八章：多元函数的微分学第一节：多元函数的极限与连续性在高等数学中，多元函数是指与多个自变量相关的函数。

多元函数的微分学则是研究多元函数的导数、极限和连续性的数学分支。

多元函数的极限是指当自变量趋于某一点时，函数值的变化趋势。

与一元函数类似，我们也可以讨论多元函数在某一点处的左极限、右极限，以及无穷远处的极限。

根据多元函数极限的定义，我们可以得到一元函数极限的特例。

多元函数的连续性则是指函数在某一点的极限等于函数在该点的函数值。

如果一个多元函数在定义域的每一点都是连续的，我们称其为连续函数。

与一元函数连续性的概念类似，多元函数的连续性包括点连续性和区间连续性两种情况。

第二节：多元函数的偏导数和全微分在研究多元函数的微分学时，最重要的概念之一就是偏导数。

偏导数是多元函数对于某个自变量的导数，而将其他自变量视为常数。

通过偏导数，我们可以研究多元函数在不同自变量方向上的变化情况。

与偏导数相关的概念是全导数和全微分。

全导数是指多元函数对于所有自变量的导数，而全微分则是全导数与自变量的微小增量之积。

全微分在多元函数微分学中具有重要的应用价值。

第三节：多元函数的微分多元函数的微分是指函数在某一点处的局部线性近似。

通过微分，我们可以求得函数在某点处的切线、法线以及在该点附近的变化情况。

多元函数的微分是通过偏导数和全微分推导而来的。

通过求得多变量的微分，我们可以进一步研究函数的最值、优化问题等。

第四节：多元函数的导数多元函数的导数是指函数在某一点处的变化率。

与一元函数的导数类比，多元函数的导数也可以用于求得函数的极值、切线与法线方程等问题。

多元函数的导数是通过偏导数推导而来的。

通过求得各个自变量的偏导数，并将其组合成一个向量，我们可以得到多元函数的导数。

第五节：多元函数的高阶导数多元函数的高阶导数是对多层次的导数求导的结果。

与一元函数的高阶导数类似，多元函数的高阶导数可以用于求函数的高阶变化率，进一步研究函数的性质和行为。

(完整版)多元函数微分学复习(精简版)

高等数学下册复习提纲第八章 多元函数微分学本章知识点（按历年考试出现次数从高到低排列）：复合函数求导（☆☆☆☆☆）条件极值-——拉格朗日乘数法(☆☆☆☆） 无条件极值(☆☆☆☆）曲面切平面、曲线切线(☆☆☆☆） 隐函数（组）求导（☆☆☆）一阶偏导数、全微分计算（☆☆☆） 方向导数、梯度计算(☆☆） 重极限、累次极限计算（☆☆） 函数定义域求法（☆)1. 多元复合函数高阶导数例 设),,cos ,(sin yx e y x f z +=其中f 具有二阶连续偏导数,求xy zx z ∂∂∂∂∂2及。

解y x e f x f xz+⋅'+⋅'=∂∂31cos ， y x y x y x y x e e f y f f e x e f y f y x zx y z ++++⋅''+-⋅''+'+⋅''+-⋅''=∂∂∂=∂∂∂])sin ([cos ])sin ([33323131222析 1）明确函数的结构（树形图)这里yx e w y v x u +===,cos ,sin ，那么复合之后z 是关于y x ,的二元函数.根据结构图，可以知道：对x的导数，有几条线通到“树梢”上的x ,结果中就应该有几项，而每一项都是一条线上的函数对变量的导数或偏导数的乘积.简单的说就是,“按线相乘，分线相加”.2）31,f f ''是),cos ,(sin ),,cos ,(sin 31yx y x e y x f e y x f ++''的简写形式，它们与z 的结构相同,仍然是y x e y x +,cos ,sin 的函数。

所以1f '对y 求导数为zu vwxx y yy x e f y f yf +⋅''+-⋅''=∂'∂13121)sin (。

《高等数学教学课件》高数-第八章-多元函数微分学

邻域U(P, ), 使U(P, ) E为空集,则
称点P为E的 外点。
边界点的定义：
若点P的任意的邻域内,既有属于E的点
也 有 不 属 于E的 点, 则 称 点P是E的 边 界 点 。
边界的定义：
E的边界点的全体称为E的 边 界 。
3、聚点、孤立点
设E是一个平面点集
聚点的定义：
若点P的任意邻域都含有E的无穷多个点，
为P0的 邻域。
0
U(P0 , ) {( x, y) 0 ( x x0 )2 ( y y0 )2 2 }
为P0的 去心邻域。
2、内点、外点、边界点
设E是一个平面点集.
内点的定义：
若点P E,并且存在P点的一个
邻域U(P, ), 使U(P, ) E,则称点P
为E的内点。
外点的定义： 若点P E,并且存在P点的一个
一切多元初等函数在其定义区域内是连续的。
例6、讨论下列函数的连续性
(1)、f
(
x,
y)
x
3 xy 2 2
y
2
x2 y2 0
解 0
x2 y2 0
当x 2 y 2 0时, f ( x, y) 3xy 是初等函数, x2 2y2
且 有 定 义, 连 续.
3kx 2
lim f ( x, y) lim
lim
x0
x2 2y4
02 2(1)4
. 2
y1
在有界闭区域上连续的多元函数的重要性质如下：
定理1、(最大最小值定理)
在有界闭区域D上连续的多元函数f , 在D上必有
最大值和最小值,亦即在D上有点P1和P2 , 使对D上任意
点P,恒有 f P1 f P f P2 , P D

高等数学第八章第三讲 多元函数的全微分

元函数全微分的概念； ２．多元函数全微分的求法； ３．多元函数连续、可导、可微的关系．
作业： 28; 29; 30.
Yu lin Polytechnic（Shen Mu Campus）
Yu lin Polytechnic（Shen Mu Campus）
上页 下页 返回
第八章
证 如果函数 z f ( x , y ) 在点P ( x , y ) 可微分,
P ( x x , y y ) P 的某个邻域
z Ax By o( )
总成立,
当y 0 时，上式仍成立，此时 | x | ,
z z 2 x 1, 2 y y ( 1,2 )
所求全微分
dz 5dx 2dy.
Yu lin Polytechnic（Shen Mu Campus）
第八章
y yz À2 Æ ¼ ã Ë ¯ º ý Ê u x sin e Ä µ « È ¢ Î · Ö . 2
[ f ( x , y y ) f ( x , y )],
Yu lin Polytechnic（Shen Mu Campus）
第八章
在第一个方括号内，应用拉格朗日中值定理
f ( x x , y y ) f ( x , y y )
f x ( x 1x, y y )x
Yu lin Polytechnic（Shen Mu Campus）
第八章
函数若在某区域 D 内各点处处可微分， 则称这函数在 D 内可微分.
如果函数z f ( x , y ) 在点( x , y ) 可微分, 则 函数在该点连续.
事实上 z Ax By o( ), lim z 0,

第八章(理工)多元函数的微分学

。
4、过曲面 z − e + 2 xy = 3 上点 (1, 2, 0) 处的切平面方程为 解析：切点的方向向量为 n = (2 y , 2 x,1 − e ) ⇒ n
z
G
G
(1,2,0)
= (4, 2, 0) = (2,1, 0) ，则有点向式 2( x −1) + ( y − 2) = 0
⇒ 2x + y − 4 = 0
∂2 z ∂ 2 w ∂u ∂ 2 w ∂v ∂ 2 w ∂u ∂ 2 w ∂v ∂2w ∂2w ∂2w 2 = − − − − = − − − ∂x 2 ∂u 2 ∂x ∂u∂v ∂x ∂u∂v ∂x ∂v 2 ∂x ∂u 2 ∂u∂v ∂v 2 ∂2 z ∂ 2 w ∂u ∂ 2 w ∂v ∂ 2 w ∂u ∂ 2 w ∂v ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w 2 = − − + + = − + + − = − + − ∂y 2 ∂u 2 ∂y ∂u∂v ∂y ∂u∂v ∂y ∂v 2 ∂y ∂u 2 ∂u∂v ∂u∂v ∂v 2 ∂u 2 ∂u∂v ∂v 2 ∂2 z ∂ 2 w ∂u ∂ 2 w ∂v ∂ 2 w ∂u ∂ 2 w ∂v ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w = 1− 2 − + + = 1− 2 − + + = 1− 2 + 2 ∂x∂y ∂u ∂x ∂u∂v ∂x ∂u∂v ∂x ∂v 2 ∂x ∂u ∂u∂v ∂u∂v ∂v 2 ∂u ∂v ∂2 z ∂2 z ∂2 z ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w ∂2w +2 + = − 2 −2 − + 2(1 − 2 + 2 ） − 2 +2 − ＝− 4 2 + 2 ∂x 2 ∂x∂y ∂y 2 ∂u ∂u∂v ∂v 2 ∂u ∂v ∂u ∂u∂v ∂v 2 ∂u
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

令
f (x , y ) A， xx 0 0
f (x , y ) B， xy 0 0
f (x , y ) C， yy 0 0
则
f
(x,
y ) 在点
(x , 0
y 0 ) 处是否取得极值的条件如下：
（ 1 ） AC B 2 0 时具有极值，
当 A 0 时有极大值， 当 A 0 时有极小值；
y 0 ) 具有偏导数，且
在点
(x , 0
y 0 ) 处有极值，则它在该点的偏导数必
然为零：
f (x , x0
y) 0
0，
f (x , y0
y) 0
0.
证 不妨设
z
f
(
x
,
y
) 在点
(
x
0
,
y 0
) 处有极大值,
则对于
(
x 0
,
y 0
) 的某邻域内任意
( x, y) ( x0 , y0 )
都有
f (x,
x0
x0
x2
k2x2
1 k2
,
y kx 0
随着
k
的取值不同，
1
k k
2
的值也不同,
故极限
lim g( x, y) 不存在.
x0
y0
三、二元函数的连续性
定义 3 设函数 z = f(x , y) 在点 P0(x0 , y0) 的 某一邻域内有定义， 如果当点 P(x , y) 趋向于点
P0(x0 , y0) 时，函数 z = f(x , y) 的极限存在， 且等 于它在点 P0 处的函数值，即
时，有
lim g( x, y) lim g(0, y) lim0 0 .
x0
y0
y0
y0
但是，当点( x , y )沿着直线 y = k x ( k 0 )趋向于点
(0, 0) 时，即当 y = k x ，而 x 0 时,
kx2
k
lim
x0
g( x,
y) lim g( x, kx) lim
x x0 y y0 z z0 . x(t0 ) y(t0 ) z(t0 ) 切向量：切线的方向向量称为曲线的切向量.
T x(t0), y(t0), z(t0)
法平面：过M点且与切线垂直的平面.
x(t0 )(x x0 ) y(t0 )( y y0 ) z(t0 )(z z0 ) 0
这就是二元隐函数的求导公式.
第三节 全微分及应用
一、全微分的概念 二、全微分的应用
一、全微分的概念
定义 如果函数 z = f ( x, y )在定义域 D 的内点P( x , y )
处的全增量
可表示成
其中 A , B 不依赖于 x , y , 仅与 x , y 有关，则称函数 f ( x, y ) 在点P( x, y) 可微，Ax By 称为函数 在点 (x, y) 的全微分, 记作
（ 2 ） AC B 2 0 时没有极值； （ 3 ） AC B 2 0 时可能有极值,
还需另作讨论．
也可能没有极值，
求函数 z f ( x , y ) 极值的一般步骤：
(x, y) 1 x2 y2 4
闭区域
y
y
o
x
o 1 2x
y
o
x
y
o 1 2x
（二） 二元函数的定义
多变量之间依赖关系举例： • 圆柱体的体积
• 定量理想气体的压强
• 三角形面积的海伦公式
r h
ba c
定义1 设非空
映射
点集 的 n 元函数 ,记作
称为定义在 D 上
点集 D 称为函数的定义域 ;数集
二、曲面的切平面与法线
设曲面方程为
F(x, y,z) 0
在曲面上任取一条通 过点M的曲线
n
T
M
x x(t)
:
y
y(t
)
,
z z(t)
曲线在M处的切向量 T {x(t0), y(t0), z(t0)},
令 n {Fx ( x0 , y0 , z0 ), Fy ( x0 , y0 , z0 ), Fz ( x0 , y0 , z0 )}
若函数在域 D 内各点都可微, 则称此函数在D 内可微.
二、全微分的应用
第四节 多元函数微分学的应用
一、空间曲线的切线与法平面 二、曲面的切平面与法线
一、空间曲线的切线与法平面
x x(t)
设空间曲线的方程
y
y (t )
z z(t)
(1)式中的三个函数均可导.
设 M ( x0 , y0 , z0 ), 对应于 t t0;
(z ) x
其中第二、三个偏导数称为混合偏导数。类似可以定义 更高阶的偏导数.二阶及二阶以上的偏导数统称为高阶偏 导数
例如，z f ( x, y) 关于 x 的三阶偏导数为
z f ( x, y) 关于 x 的 n 1 阶偏导数 , 再关于 y 的一阶偏导
数为
三、复合函数与隐函数的求导法则
（一） 复合函数的求导法则
的函数值z 趋近于一个确定的常数A， 则称 A
为函数 z = f (x , y) 当( x, y)( x0 , y0 )时的极
限，记为
lim f( x, y) A,
( x, y x0 , y0 )
或 f(x,y) A,( x, y)( x0, y0 )
例 考察函数
g( x,
y)
xy
x2 y2
若满足不等式 f ( x , y )
f
(x , 0
y) 0
，则称函数在
(Leabharlann x 0,y 0
)
有极大值；若满足不等式f
(
x
,
y
)
f (x , y ) 00
则称函数在
(
x
0
,
y 0
)
有极小值；
极大值、极小值统称为极值 使函数取得极值的点称为极值点
定理1 （必要条件）
设函数
z
f
(x,
y ) 在点
(x , 0
例如, 点 ( 0 ,0 ) 是函数 z xy 的驻点，但不是极值点.
问题：如何判定一个驻点是否为极值点？ 定理2（充分条件） 设函数 z f ( x , y ) 在点 ( x , y ) 的某邻域内连续，
00
有一阶及二阶连续偏导数，
又
f (x , x0
y) 0
0,
f (x , y0
y) 0
0，
M( x0 x, y0 y, z0 z)
对应于 t t0 t.
x
(1)
z • M
•M
o
y
割线 MM 的方程为
z
• M
x x0 y y0 z z0 x y z
x
•M
o
y
考察割线趋近于极限位置——切线的过程
上式分母同除以 t,
x x0 y y0 z z0 ,
x
y
z
t
t
t
当M M ,即t 0时 , 曲线在M处的切线方程
曲则线n，它T,们在由M于曲的线切是线曲都面与上同通一过向M量n的垂任直意，一故条 曲面上通过M 的一切曲线在点M 的切线都在同一 平面上，这个平面称为曲面在点M 的切平面.
切平面方程为
Fx ( x0 , y0 , z0 )( x x0 ) Fy ( x0 , y0 , z0 )( y y0 ) Fz ( x0 , y0 , z0 )(z z0 ) 0
若函数f(x, y)在点 P0(x0, y0) 处不连续，则称P0
为函数f(x, y)的间断点
两个结论
（1）若函数 f（x，y）在有界闭区域 D 上连 续，则 f（x，y）在 D 内必有最大值和最小值
（2）若函数 f（x，y）在有界闭区域 D 上连
续，则 C 是介于最大值和最小值之间的实数，则 在 D 内至少存在一点（x0，y0），使得
f（x0，y0）=C
第二节 偏导数
一、偏导数的概念及几何意义 二、高阶偏导数 三、复合函数与隐函数的求导法则
一、偏导数的概念及几何意义
（一） 偏导数的概念
定义 设函数
在点
的某邻域内极限
存在,则称此极限为函数 的偏导数，记为
注意:
同样可定义对 y 的偏导数为
若函数 z f ( x, y)在域 D 内每一点 ( x, y)处对 x
x x0 y y0 z z0 . f x ( x0 , y0 ) f y ( x0 , y0 ) 1
第五节 二元函数的极值与最值
一、二元函数的极值 二、二元函数的最值 三、条件极值
一、二元函数的极值
设函数 z f ( x , y ) 在点 ( x , y ) 的某邻域 00
内有定义，对于该邻域内异于 ( x , y ) 的点 ( x , y ) 00
若 Fy 0, 则
Fx
Fy
dy dx
0
,
这就是一元 隐函数的求导公式.
设方程 F (x , y , z) = 0 确定了隐函数 z = z (x , y),
若 Fx，Fy，Fz 连续， 且 Fz 0, 两边分别对 x ，y 求 导， 得
Fx
Fz
z x
0,
Fy
Fz
z y
0.
因为Fz 0, 所以
有界区域 区域是有限的，如圆形区域，矩 形区域等
无界区域 区域能够延伸到无穷远处 区域的边界 围成区域的曲线 闭区域 所考虑的区域包含区域的全部边界 开区域 所考虑的区域不包括区域的边界
例如，在平面上
(x, y) x y 0