数字下变频仿真

I
时钟 重
配置
I_W
S W
Q 2选1 I_N BUS
MUX
多相滤波结
2
构的宽带滤 Q_W 选
M c
I Q_N
波器
1B
中频
IT
S
AD 信号
C
6645
NCO Q H
BP U 接口 输
S
出
开关
S
配置
至
FPGA EP2S60F672C4
I Q
I_N W
窄带滤
I
波器组 Q_N T
C
I_N Q_N
M 参数 U DDC X 参数
…
−2π −π −ω1 0 ω1 π 2π ω
(a)下变频前实信号频谱
X (e jω )
−ω1 0
ω
(b)复本振信号频谱
X (e jω )
A
…
…
−2ω1 0 2ω1
ω
(c)混频后的信号频谱
图 4 数字下变频完成的频谱搬移
2) 数字下变频器两种典型结构
a) 传统窄带数字下变频结构
图 5 传统窄带数字下变频结构
本系统的数据流程如图 1 所示，A/D 采样的中频模拟信号输出至 FPGA， FPGA 中的 VB-DDC 将中频信号下变频至基带，再通过 McBSP 接口将基带信号 传给 DSP 进行解调、功率谱估计等数字信号处理，最后 DSP 再将结果通过以太 网送至上位机 PC 进行显示。同时，VB-DDC 可通过 McBSP 接口接受上位机 PC 传来的配置参数，实现 DDC 的动态配置。
Receivers. The Variable-Bandwidth Digital Down-Converter (VB-DDC) ,which is suitable for Wideband Digital Receiver, is implemented in FPGA chip Stratix II EP2S60F672C4. The VB-DDC combines the advantages of traditional digital down-conversion architectures and poly-phase filter architectures, realizes efficient high-speed processing for input IF signal, and could configure the bandwidth of signal processing flexibly in a large range. Hardware test result shows the effectiveness of this design.

数字下变频电路的FPGA实现随着数字化时代的到来，数字信号处理技术已经成为了许多领域中不可或缺的一部分。

其中，数字下变频技术是一种非常重要的数字信号处理技术，被广泛应用于雷达、通信、音频处理等领域。

本文将介绍数字下变频电路的FPGA实现。

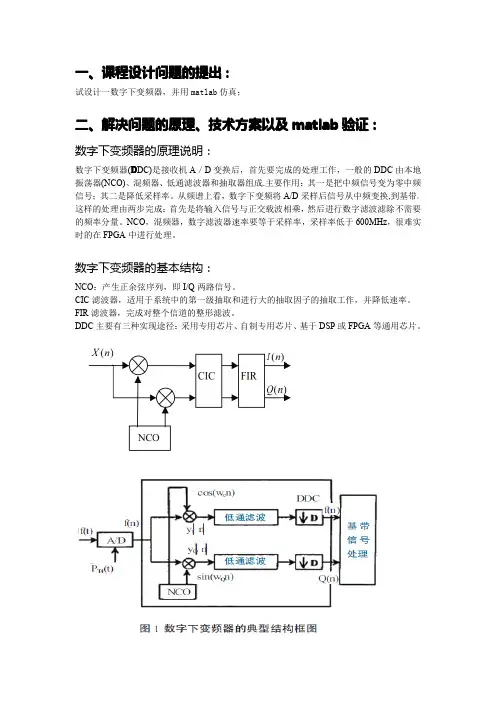
数字下变频电路的基本原理数字下变频电路的基本原理是将输入信号进行混频，将高频信号转换为低频信号，并对低频信号进行采样和滤波，得到一个纯净的低频信号。

数字下变频电路通常由数字信号处理器、数字乘法器和数字低通滤波器等组成。

FPGA实现数字下变频电路的优势 FPGA（Field Programmable Gate Array）是一种可编程逻辑器件，能够根据需要实现各种数字电路。

与传统的数字信号处理芯片相比，FPGA具有以下优势：高速并行处理能力：FPGA内部具有大量的可编程逻辑器件，可以实现高速并行处理，提高处理速度和效率。

灵活性：FPGA可以通过重新编程实现不同的数字电路，方便灵活，可以快速适应不同的应用场景。

可靠性：FPGA内部具有严格的质量保证措施，保证了数字电路的可靠性和稳定性。

设计数字下变频电路的算法：根据具体应用场景和要求，利用MATLAB 等软件设计数字下变频电路的算法。

将算法转换为硬件描述语言：将设计的数字下变频电路算法转换为硬件描述语言（如VHDL或Verilog），并利用EDA工具进行仿真和验证。

将硬件描述语言编译成二进制文件：将生成的硬件描述语言编译成二进制文件，以便在FPGA上实现。

将二进制文件下载到FPGA中：将生成的二进制文件下载到FPGA中，通过调试和测试，最终实现数字下变频电路。

结论数字下变频电路的FPGA实现具有高速并行处理能力、灵活性和可靠性等优势，已经被广泛应用于雷达、通信、音频处理等领域。

通过设计算法、转换为硬件描述语言、编译成二进制文件以及下载到FPGA中等步骤，可以实现数字下变频电路的高效、快速和可靠实现。

数字下变频电路是一种重要的信号处理单元，它在通信、雷达、电子对抗等领域有着广泛的应用。

闸门
门控
B 放大 整形
S2
1000Tx
1Tx
10Tx 100Tx
÷10
÷10
计数锁存译码 显示系统
÷10
四、实验参考电路
（1）控制时序产生电路
图4.8.5 是由秒脉冲发生器（可由晶体振荡器和 多级分频器组成）和可重触发单稳态74LS123 组成
的控制时序产生电路。秒脉冲发生器产生脉冲宽度 为的定时脉冲，74LS123单稳态电路产生锁存和清 零脉冲。（仿真软件Multisim 8的元件库中，没有 74LS123单稳态电路，可用555定时器组成单稳态 电路）。 5V
4. 闸门电路
闸门电路由与门组成，该电路有两个输入端和一 个输出端，输入端的一端，接门控信号，另一端接 整形后的被测方波信号。闸门是否开通，受门控信 号的控制，当门控信号为高电平“1”时，闸门开启； 而门控信号为低电平“0”时，闸门关闭。显然，只 有在闸门开启的时间内，被测信号才能通过闸门进 入计数器，计数器计数时间就是闸门开启时间。可 见，门控信号的宽度一定时，闸门的输出值正比于 被测信号的频率，通过计数显示系统把闸门的输出 结果显示出来，就可以得到被测信号的频率。
5. 电子计数器测量周期
当被测信号频率比较低时，用测量周期的方法来 测量频率比直接测量频率有更高的准确度和分辨率， 且便于测量过程自动化。该测量方法在许多科学技 术领域中都得到普遍使用。图4.8.4是用电子计数器 测量信号周期的原理方框图。
晶振
Tx
时基 分频
1µs
S1 Tc
10µs 1ms 100µs Tx1
①可控制的计数、锁存、译码显示系统； ②石英晶体振荡器及分频系统（可用Multisim 8中
的函数发生器替代）；

第四章数字下变频器设计验证和逻辑综合。阐述整个设计过程所用到的验证方法，分模块给出了RTL级设计仿真结果,并分析验证功能的正确性。接着对比并分析了整体的Matlab仿真结果和Modelsim的仿真结果。最后介绍了芯片逻辑综合的流程、优化方法以及综合策略，利用Design Compiler完成芯片的逻辑综合，并给出综合报告。
在早期的雷达收发系统中，都是采用模拟器件来实现各个功能模块，设计过程中经常会出现温度漂移、增益变化等问题.相对于模拟电路来说，数字电路具有可自检、可编程等优点,上面所述的系统很多部分都已经逐步数字化.在数字化进程中,数字信号处理技术的应用也受到了雷达系统研究工作者的重视,成为相关积累(如FFT、数字滤波、脉冲压缩等）、非相关积累（视频积累）、目标检测以及图像处理等功能的技术保证。随着数字信号处理理论的不断成熟和完善，微电子技术的飞速发展，雷达技术和其它的电子信息化技术的发展，尤其是软件无线电技术的兴起，更加方便了雷达数字化系统的实现。在这样的发展趋势下，除了微波发射和射频部分，整个雷达系统将全部由数字电路实现，在数字信号处理的优势能得到全面的发挥的同时，还使具有体制标准化、系统数字化，功能模块化，低功耗，高度开放性以及灵活性等性能,这将成为了现代雷达系统的关键技术和发展趋势［]。在现今的高科技发展的时代,人们纷纷打起的信息战和电子战,雷达系统在其中扮演的角色尤为重要。为了能更好的适应现代战争的需求，对现今的雷达系统也提出抗干扰、反隐形，具有高分辨力以及强大的自我生存等能力，高要求的提出，使得雷达信号处理技术的研究也得到了快速的进步.目前雷达信号处理正在由视频处理阶段向中频处理阶段迈进,目的就是实现雷达中频以下的处理全部数字化，研究热点.
微系统设计、测试与控制
课程大作业之
基于FPGA的DDC(数字下变频）的设计与仿真

function [y, t]=dds_matlab(fout, Fs, Bits, endtime) t=2*pi*(0:2^Bits-1)/2^Bits; LUT=sin(t); subplot(2,1,1) plot(t, LUT) figure(1); grid on
t=0:1/Fs:endtime; N=length(t); n=1; y=zeros(1, N); IND=zeros(1, N); % Input Frequency Word k=floor(fout/Fs*2^Bits); index=0;
%输入原始信号
b = firhalfband(18,0.00245,'dev'); % 获得设计的半带滤波器抽头系数
impz(b);
% 半带滤波器的冲击响应
h = mfilt.firdecim(2,b);
figure
y_fi = filter(h,x);
x = double(x);
y = double(y_fi);
11000
1001
0.809
11010
1010 1011 1100 1101 1110 1111
0.866 0.914 0.951 0.978 0.994 1.000
Matlab程序： %fout: Output frequency %Fs: Sample frequency %Bits: Number of bits of the LUT %endtime: Expectedቤተ መጻሕፍቲ ባይዱsimulation endtime %y: Output sine wave %t: Output time
址吗对数据 ROM 进行寻址。
地址码
幅度（满度值为 1）

数字下变频和数字上变频在超外差式接收机中，如果经过混频后得到的中频信号比原始信号低，那么此种混频方式叫做下变频（Down Converter or DC）。

将射频信号通过一次或者几次的模拟下变频转换到中频上，在中频对信号数字化，然后再进行数字下变频。

数字下变频（Digital Down Converter or DDC）是软件无线电的核心技术之一。

可以把数字下变频分为两个基本的模块，数控振荡器：NCO(Nu-merical Control Oscillator)混频模块和抽取滤波模块。

其中NCO模块产生正余弦波样本值，然后分别与输入数据相乘，完成混频。

抽取滤波模块常用的结构是积分梳状抽取滤波器(CIC)级联后再与多级半带滤波器(HBF)的级联。

如果信号带宽比较宽，抽取倍数不是很大，可以采用FIR滤波器。

当输入信号采样速率很大的时候，则可以采用多相滤波的下变频方案，把运算环节安排在抽取之后，这种结构大大降低了对数据处理速度的要求。

数字上变频DUC(Digital Up Converter)，无线电发射链路中，数字信号经过转换成模拟信号，模拟信号经过混频后得到比原始信号高的期望的射频中心频率，然后信号经过放大到适当的功率电平，最后经过限制带宽后经天线发射出去。

这种混频频率向上变化的方式叫做上变频。

数字上变频（DUC）是软件无线电的核心技术之一。

数字上变频器(DUC)和数字下变频器(DDC)不仅仅是通信应用(如软件无线电)中的关键，而且在需要窄带信号高速流的应用中也是重要的。

另外，DDC结构容易控制所有取样速率下的混淆防止分样。

做为1个例子，让我们看看数字记录5MHz带宽(中心在50MHz)信号的问题。

此信号可以是来自RF-IF模拟下变频器的信号或者是直接从天线接收的信号。

为了满足尼奎斯特准则，我们需要以105ms/s取样率取样此信号。

然而，为了合理地捕获此信号，应该在较高的取样率(至少200ms/s)取样此信号。

技术报告软件数字下变频的实现与算法分析李玉柏,彭启琮(电子科技大学通信与信息工程学院,四川成都 610054)摘 要:数字下变频(DDC)技术将宽带大数据流信号变成窄带低数据流信号,以便DSP 实时处理。

本文在分析数字下变频的基本模型基础上,提出了软件数字下变频的一种实现方案,给出了相应的算法和算法分析,以及在数字接收机中的应用。

软件数字下变频比常规DDC 专用芯片有更大的灵活性、适应性和更高的处理中频。

关键词:数字下变频;软件无线电;实时处理;载波恢复中图分类号:TM9191 文献标识码:B 文章编号:1000-436X(2000)10-0044-06Software implementation and algorithm analysis of DDCLI Yu -bai,PENG Q-i cong(Ins titute of Comm 1&info 1Eng 1,UESTC,Chengdu 610054,China)Abstract :Wide band high bi -t rate digital signal can be transformed to narrow band low bi-t rate digi tal signalwi th DDC technology,so can be processed by DSP i n rea-l ti me 1After analysing the model of DDC technology,asoftware implementation methods of DDC,which have more efficiency,more flexibili ty and adaptabili ty than nor -mal DDC ASIC,are presented 1Key words :DDC;sof-t radio;rea-l ti me processing;carrier recovery1 引言软件无线电的基本思想是将宽带A P D 变换尽可能地靠近射频天线[1](即尽可能早地将接收到的模拟信号数字化),尽量通过软件来实现电台的各种功能。

数字下变频基于FPGA的软件设计与实现【摘要】雷达的数字下变频功能主要是将天线接收到的中频回波信号通过A/D变换后，进行数字下变频处理，转为两路I/Q基带数据。

本文主要设计了一种基于FPGA的数字下变频方法，通过对数字控制振荡器（NCO）及低通滤波器（FIR）的设计及实现，完成了对于不同频率本振信号的数字下变频处理。

结果表明，基于该方案设计的数字下变频功能已在实际系统中得到应用。

【关键词】数字下变频（DDC）；FPGA；数字滤波器【Abstract】The function of DDC is mainly to convert the signal received after A/D conversion by the antenna to Digital Down Convert（DDC），finally into two I/Q baseband data. This paper mainly design a method about Digital Down Conversion based on FPGA，by designing the numerically controlled oscillator （NCO）and a low-pass filter （FIR），to convert different frequency signal with DDC. The results showed that the conversion function has been used in the actual system.【Key words】DDC（Digital Down Convert）；FPGA；FIR Filter0 引言软件无线电是现今无线通信系统的关键技术，其核心思想是让数字化处理功能尽量的靠近天线，从而将更多的处理通过数字的方式完成。

[1]而数字下变频是软件无线电的关键部分，主要完成对信号的AD变换、混频、滤波以及抽取等工作，包括数字混频模块和抽取滤波模块。

显 然 ， 于 截 取 的窗 函数 不 同 ， 得 到 的 滤 波 器 的性 能 就 用 所
得 ， 们 用 瑟 时阶 Ｎ ； 出 我采凯窗 ， ＝ ｝ 当 数 －
１ 次 每秒 。 ０
ｌ２， ＝９由 ４． １
不 一 样 。常 用 的 窗 函数 有 ：
ｆ矩 形 窗 ： １ ）
ｆ ，０≤ ｎ≤ Ｎ－１ １
（凯 泽 （ａ ｅ） ： ４ ） Ｋ ｉｒ ｓ 窗
， 、
ｐ、１［ ｎＮ １２Ｉ ）０ ≤ － Ｊ（ ／－１２／ －） ／ ｐ， ≤ｎ Ｎ １ Ｉ ｏ － （ ］ ｏ ）（
【， ０ 其 他
５仿 真 分 析
５１浮 点 仿 真 ．
假设 我们取７ ｏ ０ １ ８ Ａ ０ ０ 个 ２ Ｑ Ｍ信 号值 ， 频谱 图如 图 ２ 其 所示 。
§ｌ… … ：Ｔ０ 矗 －＿… ．；… … ５．． … － 口 ．ｊ ｊ ＿ … … ０ ＿ ＿ ＿ ： ＿
ｏ ｝ ¨ ｝＿｝ ［ ｌ
Ｎ。．１－ ｅｄＦ ｅ ｕ ｎ ｒａ ｚ ｑ ｅ ｜ ｒ
— 育 奇—
（ ｓ ａｍｐｅ ｌ）
法可设计出性 能优越的滤波器。随着计算机辅助设计 的普及 ，
图 ２输 入 信 边缘频率 。
等 波 纹法 又 叫最 佳 一 致 逼 近 法 ， 波 纹 法 是 以 最 大 误 差 最 等 小 化 为 优 化 准则 来 进 行 设 计 的 ， 一 定 意 义 上 对 希 望 的 频率 响 在
采 用 等 波纹 法设 计 的 滤波 器 幅 度 与相 位 如 图 ３ 示 。 所
其 中 ， 是第 一 类 贝 塞尔 函数 ， 用 幂 级 数展 开 来 计算 ： Ｉ 可
一 ㈣ ≯ ＋ ＋ ＋ 一 。 ・

a lg orithms a s CIC, HB, FIR of e a c h mod ule in d own- c onve rs ion, d is c us s ion, a b s tra c tion a nd s umma riza tion a re g ive n in this p a -
（3）
通过低通滤波器可以得到
I'(n)=
A 2
cos[φ(n)]
Q'(n)=- A sin[φ(n)] 2
（4）
由于 ADC 在中频进行采样，采样速率有可能很高，而混
频后得到的数据率和采样速率是一致的，后级的 FIR 滤波器
根本无法达到这个处理速率，因此先通过 CIC（级联积分梳
状）和 HB（半带）滤波抽取器进行大的抽取，使数据率快速降
需要强调的是，在设计时，必须综合考虑 CIC、HB 和 255 阶 FIR 三种抽取滤波器，才能设计出最优数字信道。
4 数字下变频器的功能仿真及结果
将各个滤波器模块级联起来，将各算法融为一体，从软件 实现的角度完成对数字下变频系统的搭建，该下变频系统的 框图如图 5 所示：
And a ny mod ule is p ut tog e the r s o tha t s ys te m found a tion is c a rrie d out a nd the s ys te m func tion is s imula te d in s oftwa re . The re -
摘 要：文中应用软件无线电思想对数字下变频器中的几个关键技术进行了研究，对下变频各个模块所涉及
到的 CIC、HB、FIR 等关键算法进行了讨论、提炼与总结，应用 matlab 软件设计了下变频器中的 CIC、HB、FIR

Your company slogan
原理和结构
原理：数字下变频器(DDC)是接收机A／D变换后，首先要完成 数字下变频器(DDC)是接收机 是接收机A 变换后，
的处理工作，一般的DDC由本地振荡器(NCO)、混频器、 由本地振荡器(NCO)、混频器、 的处理工作，一般的DDC由本地振荡器 低通滤波器和抽取器组成.主要作用： 低通滤波器和抽取器组成.主要作用：其一是把中频信号 变为零中频信号；其二是降低采样率。从频谱上看， 变为零中频信号；其二是降低采样率。从频谱上看，数字 下变频将A/D采样后信号从中频变换到基带 采样后信号从中频变换到基带。 下变频将A/D采样后信号从中频变换到基带。这样的处 理由两步完成：首先是将输入信号与正交载波相乘， 理由两步完成：首先是将输入信号与正交载波相乘，然后 进行数字滤波滤除不需要的频率分量。NCO，混频器， 进行数字滤波滤除不需要的频率分量。NCO，混频器， 数字滤波器速率要等于采样率，采样率低于600MHz， 数字滤波器速率要等于采样率，采样率低于600MHz， 很难实时的在FPGA中进行处理 很难实时的在FPGA中进行处理
总结：离散信号的精确性与寄存器长度相关，寄存器长度越长，精确 总结：离散信号的精确性与寄存器长度相关，寄存器长度越长， 度越高，硬件实现却越复杂。多路相位合成滤波器在DDC并行 度越高，硬件实现却越复杂。多路相位合成滤波器在DDC并行 处理过程中不会产生其他噪声， 处理过程中不会产生其他噪声，因此在并行处理过程中信噪比 的分析等同于传统的DDC结构 结构。 的分析等同于传统的DDC结构。
FIR滤波器 FIR滤波器: 滤波器:
Your company slogan
论文主体
1.并行处理结构： 并行处理结构： 抽取滤波器模块通过多相滤波器结构降低采样率和实现低通滤波。 抽取滤波器模块通过多相滤波器结构降低采样率和实现低通滤波。

电子科技大学实验报告学生姓名：学号：指导教师：一、实验室名称：通信信号处理及传输实验室二、实验项目名称：数字上下变频三、实验原理：1、数字上/下变频的理论基础通常的无线通信都是通过载波调制信号来实现。

这意味着产生了数字基带信号后，需要将信号通过数模（DA）转换，由射频端调制到某个载波频段进行发送。

这个将基带信号调制到高频载波频段的过程就称为上变频。

反之，在接收机端将模数（AD）转换后的高速率高频带数字信号转换为低速率的基带信号，即将中频或者高频信号搬移到基带或者低频波段的过程就称为下变频。

因此，上变频和下变频的概念分别是指把信号搬移到更高或更低的频率上。

这可以通过信号()t c与一个复旋转向量相乘得到，结果为：()()t f j c=t sπ2t cef代表搬移的频率，通常称为载波频率。

其中，c复数信号的实部和虚部也可以分别称做同相分量或正交分量。

数字上变频和下变频就是对上式进行数字化。

这就意味着信号和复向量都要用量化的样本来表示。

引入满足采样定理的采样周期T，这样，数字上变频和下变频可以写为：()()kT f j c e kT c kT s π2=。

进行上变频还是下变频是由频率c f 的符号决定。

因此只要对其中一种情况进行讨论即可。

我们假设对接收到的信号在模拟前端对整个接收带宽进行下变频，然后进行滤波。

假设信道可位于带宽为Band 的频带(波段)内的任何位置，频带内包含所需信道加上干扰邻道。

如图1所示。

对信号进行下变频可以得到图2。

邻道干扰可以通过信道化滤波器来滤除。

图1 下变频前信号信道示意图图2 下变频后信号信道示意图为了分析方便，我们假设中频信号为单频形式，暂不考虑邻道及其他干扰。

1）数字下变频的时域分析：数字下变频的目的是把所需的分量从载波频率加搬移至基带。

模拟中频信号为单频形式：()()0cos c c t t ωϕ=+其中c ω表示信号频率，0ϕ表示信号初始相位。

同时假设用于正交解调的两路数字本振的初始相位为0，那么模拟中频信号c c c c经过A/D 后得到的信号形式为()()()()()[]∑+∞-∞=-⨯=⨯=k T kT t kT c t P t c kT C δ。

数字下变频仿真原理：信号采样的频谱调频信号：02()cos *(2/2)s x K t n f nt π=+/MHz0002202*cos(2/)cos(2)cos(2)cos(4*/2*/2)cos(*/2)s s s s x f n f f nt f nt f nt K t K t K t ππππ=+=++0002022*sin(2/)cos(2)sin(2)sin(*/2*/2)sin(*/24)s s s s K t Kt K x f n f f nt f nt f nt tππππ+-=-+=-+因为f 0=30MHz ，整体向左平移30MHz 。

-40-20带宽为5MHzx n的时域波形和频域波形，如下图所示。

通过仿真得到()clc;clear all;close all;f0=30e6; 中心频率B=5e6; 带宽T=30e-6; 脉冲宽度fs=40e6; 采样频率N=T*fs; 采样点数K=B/T; 频率变换率ts=1/fs; 采样周期t=-T/2:ts:T/2-ts;x=cos(2*pi*(f0*t+K*t.^2/2));figure(1);title('时域波形');xlabel('point ');figure(2);plot(abs(fft(x)));title('频域波形');xlabel('point');I路信号和Q路信号：ddc_i = x.*cos(2*pi*f0*(1:N)/fs); I路信号ddc_q = -x.*sin(2*pi*f0*(1:N)/fs); Q路信号figure(3);subplot(211);plot(t,ddc_i);grid;title('I路波形');subplot(212);plot(t,ddc_q);grid;title('Q路波形');FIR滤波器的设置在mand Windows里输入fdatool进入滤波器参数设置的界面Hd=fir;[h,f]=freqz(Hd,512);figure(4);plot(f,20*log10(abs(h)));gridtitle('FIR低通滤波器的幅频特性响应') hd=Hd.Numerator;fir_i=conv(ddc_i,hd);fir_q=conv(ddc_q,hd);figure(5);subplot(211);plot(fir_i);gridtitle('FIR低通滤波器后的I路信号'); subplot(212);plot(fir_q);gridtitle('FIR低通滤波器后的Q路信号');s=fir_i+j*fir_q;figure(6);subplot(211);sf=fftshift(abs(fft(s)));plot(sf);grid;title('信号滤波后的频谱')subplot(212);plot((20*log10(sf/max(sf))));grid title('归一化频谱')clc;clear all;close all;f0=30e6;B=5e6;T=30e-6;fs=40e6;N=T*fs;K=B/T;ts=1/fs;t=-T/2:ts:T/2-ts;x=cos(2*pi*(f0*t+K*t.^2/2)); figure(1);plot(x);title('时域波形');xlabel('point');figure(2);plot(abs(fft(x)));title('频域波形');xlabel('point');ddc_i = x.*cos(2*pi*f0*(1:N)/fs); ddc_q = -x.*sin(2*pi*f0*(1:N)/fs); figure(3);subplot(211);plot(t,ddc_i);grid;title(' I路波形');subplot(212);plot(t,ddc_q);grid;title(' Q路波形');Hd=fir;[h,f]=freqz(Hd,512);figure(4);plot(f,20*log10(abs(h)));gridtitle(' FIR低通滤波器的幅频特性响应') xlabel('w/pi');hd=Hd.Numerator;fir_i=conv(ddc_i,hd);fir_q=conv(ddc_q,hd);figure(5);subplot(211);plot(fir_i);gridtitle(' FIR低通滤波器后的I路信号'); subplot(212);plot(fir_q);gridtitle(' FIR低通滤波器后的Q路信号');s=fir_i+j*fir_q;figure(6);subplot(211);sf=fftshift(abs(fft(s)));plot(sf);grid;title('信号滤波后的频谱')subplot(212);plot((20*log10(sf/max(sf))));grid title('归一化频谱')。

1 引言数字下变频DDC(digital down lonvwrsionl作为系统前端A／D转换器与后端通用DSP器件间的桥梁，通过降低数据流的速率，将低速数据送给后端通用DSP器件处理，其性能的优劣将对整个软件无线电系统的稳定性产生直接影响。

采用专用DDC器件完成数字下变频，虽具有抽取比大、性能稳定等优点，但价格昂贵，灵活性不强，不能充分体现软件无线电的优势。

FPGA工艺发展迅速，处理能力大大增强，相对于ASIC，DSP，其具有吞吐量高、开发周期短、可实现在线重构诸多优势。

基于这些优点，FPGA在软件无线电的研发中具有重要作用。

2 数字下变频系统数字下变频器在软件无线电系统中完成的功能结构如图1所示，其中包括直接数字频率合成器DDS(direct digital synthesizer)、数字混频器、FIR滤波器、抽取等模块。

原始模拟中频信号经A／D转换器带通采样后得到数字中频信号，输入DDC后先与DDS产生的两路正交本振信号相乘(数字混频)，将数字中频搬移到基带。

混频后得到的数据率和采样率一致，后级FIR滤波器要达到该处理速率。

硬件实现相当困难，因此首先通过抽取模块大大降低数据速率，然后使用高阶FIR低通滤波器对整个信道整形滤波。

滤波输出的两路正基带信号交由下一级DSP器件进行处理。

2．1 混频器的FPGA实现数字混频器将原始采样信号与查找表生成的正、余弦波形分别相乘，最终得到两路互为正交的信号。

由于输入信号的采样率较高，因此要求混频器的处理速度大于等于信号采样率。

单通道的数字下变频系统需要两个数字混频器．也就是乘法器。

XC2V1000器件内嵌64个18×18位硬件乘法器，其最高工作频率为500 MHz，因此采用硬件乘法器完全能够满足混频器的设计要求。

使用Xilinx公司的Multiplier IP核可以轻松实现硬件乘法器的配置。

该设计中采用两路14位的输入信号，输出信号也为14位。

数字下变频的设计及其在FPGA中的实现作者：王平李建海刘保华马二涛来源：《现代电子技术》2010年第01期摘要:分析数字下变频结构及其实现方法,重点研究如何基于FPGA实现数字下变频的功能,并通过仿真分析验证该实现方法的正确性。

结果表明,该实现方法可用于各类数字通信系统中频信号的数字下变频处理,具有一定的实用价值。

关键词:数字下变频;混频器;数字滤波器;FPGA中图分类号:TP274文献标识码:A文章编号:1004-373X(2010)01-055-03Design of Digital Down Converter and Its Implement Based on FPGAWANG Ping,LI Jianhai,LIU Baohua,MA Ertao(Airforce Engineering University,Xi′an,710038,China)Abstract:The configuration of digital down converter and its implement method are analysed,and how to realize digital down converter′ function based on FPGA in stress is studied,the correctness of the method is validated by simulation. The results indicate that the method can be used in many kinds of intermediate frequency digital down converter processing,thus it has definite practicality value.Keywords:digital down conversion;mixer;digital filter;FPGA0 引言自20世纪90年代以来,软件无线电技术引发了移动通信领域的一场革新,数字下变频技术是软件无线电技术实现过程中的一个重要环节,其完成的任务主要是:一方面将包含所有信道的宽带信号进行信道分离,分别提取需要的窄带信号;另一方面,对于分离的窄带信号,可以大大降低其采样速率,即降低数据量,缓解基带部分的处理压力[1]。

数字频率计设计与仿真1 引言在现代电子技术中，频率是基本的参数之一，并与许多电子参量的测量方案和测量结果有密切的关系。

因此我们对于频率的认识显得就更为重要。

频率的测量方法有很多，其中数字频率计具有测量精度高、使用方便和测量迅速等优势，是目前测量频率的主要手段。

Multisim 是以Windows 为基础的一种仿真工具，适合用于数字电路或者模拟电路的设计工作。

它有直观的捕捉和强大的仿真功能，能够轻松，快速，高效对电路图进行设计和验证。

图1-1 频率计方框图数字频率计是一种最基本的测量仪器，是通信设备、计算机应用、音频视频设备等等科研生产领域里不测或缺的测量设备之一，是一种用十进制数字显示被测信号的频率的数字的测量仪器，迄今为止已经有几十年的发展历史，频率计的基本功能是用来测量三角波信号、正弦波信号及方波信号等单位时间内变化的物理量。

因而其实际运用范围是很广泛的。

在早期，人们对于数字频率计的研究主要表现在扩大测量范围和提高精确度，而这些技术现在已日却成熟，现在人们对数字频率计又提出很多新的要求，例如价格低，操作方便，高精度，高稳定度甚至还包括数据处理和分析功能。

较老的频率计是输主门 十进制计数器显示器主门触发器 十进制计数器时基振荡器 输入放大器多芯片同步十进制技术，新型频率计要求芯片的数量要少，这样器件越少的话对于频率计的技术就会更准确，误差也会越小。

一个基本的频率计的方框图如图1-1所示。

而本课题涉及的主要内容是对输入信号的整形，闸门电路控制输入信号，以及对脉冲的计数，锁存和译码，通过该项设计可以将数字电路和模拟电路的理论知识运用到实际的设计中去，具有方便快捷，容易测量等特点。

2 选择测量方式信号频率指的是信号在单位时间内周期信号变化的次数，其表达式可写为f=N/T ，其中f 指被测信号的频率，N 为信号所累计的脉冲的个数，T 是产生N 个脉冲所需要的时间参数。

该表达式其所记录的结果就是被测信号的频率。

2.王静;杨梅;刘涛 半带抽取有限冲激响应滤波器的应用设计及仿真[期刊论文]-大连海事大学学报 2004(2) 3.李义宁;赵杭生;朱爱华 CIC滤波器实现过程中应注意的几点问题[期刊论文]-军事通信技术 2004
4.飞思科技产品研发中心 Matlab 7辅助信号处理技术与应用 2005 5.Walter Tuttlebee 软件无线电技术与实现 2004 6.Nicholasetal H T The Optimization of Direct Digital Fre-quency Synthesizer Performance in the Presence of Finite Word Length Effects 1988 7.钮心忻;杨义先 软件无线电技术与应用 2001
数，然后在Ｘｉｌｉｎｘ公司ＩＳＥＳ．２开发环境下，使用Ｖｅｒｉｆｏ萨言编程实现。最后对基于ＦＰＧＡ实现的数字下变频系统调Ｍｏｄｅｌｓｉｍ
进行仿真测试。验证了设计的正确性。
关键词：软件无线电；数字下变频；ＸｉｌｉｒＬｘ；数字滤波器
１引言 在软件无线电接收机的设计中，数字下变频器（ＤＤＣ）技术是 其核心技术之一。数字中频软件无线电接收机由模拟预处理、 ＡＤＣ、ＤＤＣ和高速ＤＳＰ组成。一般Ａ／Ｄ采样都是在中频以上，其 频率一般在ＭＨｚ数量级以上。一般认为，要进行较好的滤波等 处理，需要对每个采样点进行１００次操作。对于一个软件无线电 系统来说，若系统带宽为１ ０ＭＨ乙要大于２５ＭＨｚ。这样就需要 ２５００ＭＩＰＳ（百万指令每秒），这是现有的任何单个ＤＳＰ很难胜任 的１ｌｌ。因此，必须采用数字下变频技术，通过对数字信号进行采 样率变换以缓解ＤＳＰ处理速度的压力。作为过渡阶段的软件无 线电用ＤＤＣ实现中频段的处理任务，这样即能保留软件无线电 的优点，又有较高的可靠性“’。 目前，国外虽已生产专用数字下变频芯片，其具有抽取比 大、性能稳定等优点，但专用数字下变频芯片价格昂贵、灵活 性不强，不能充分体现软件无线电的优势。用ＦＰＧＡ来实现比用 专用芯片具有更多的好处，ＦＰＧＡ器件具有很强的稳定性和高 效的处理能力，它可以工作在几十甚至上百ＭＨｚ的频率上，其 高速强大的处理能力，是实现数字中频处理的理想器件。使用 ＦＰＧＡ芯片实现的下变频器件可以更加方便的采用软件方法将存 储器、控制器等外围器件集成到芯片内部，提高了整个系统的 稳定行和集成度。虽然用硬件实现，ＦＰＧＡ的重复可配置能力， 使其可以根据不同的系统要求，采用不同的结构来完成相应的 功能，具有很强的灵活性，便于进行系统功能扩展和性能升 级。并且设计和修改非常容易，其灵活性与方便性与软件实现 相差无几，适合软件无线电灵活性。