安徽省六安市2016年高一数学理暑假作业第三十一天Word版含答案

第31天 概率课标导航：1.了解随机事件发生的不确信性与频率的确信性，了解概率的意义；2.明白得古典概型及其计算公式，会计算一些随机事件的概率.一、选择题1. 从装有2个红球和2个黒球的口袋内任取2个球，那么互斥而不对立的两个事件是 （ ）A ．至少有一个黒球与都是黒球B ．至少有一个黒球与都是黒球C ．至少有一个黒球与至少有1个红球D ．恰有1个黒球与恰有2个黒球2. 已知事件“在矩形ABCD 的边CD 上随机取一点P ，使△APB 的最大边是AB ”发生的概率为12，则AD AB＝ ( )3. 一组抛物线2112y ax bx =++，其中a 为2,4,6,8中任取的一个数，b 为1,3,5,7中任取的一个数，从这些抛物线中任意抽取两条，它们在与直线1x =交点处的切线彼此平行的概率是 （ ）A ．112B ．760C ．625D ．15 4. 甲、乙、丙、丁4个足球队参加竞赛，假设每场竞赛各队取胜的概率相等，现任意将这4个队分成两个组（每组两个队）进行竞赛，胜者再赛，则甲、乙相遇的概率为 （ ）A ．16B ．14C ．13D ．125. 连掷骰子两次取得的点数别离记为a 和b ，则使直线340x y -=与圆22()()4x a y b -+-=相切的概率为( ) A ．136 B ．118 C ．112 D ．196. 考察正方体6个面的中心，从中任意选3个点连成三角形，再把剩下的3个点也连成三角形，则所得的两个三角形全等的概率等于 （ ）B. 12C. 13D. 0 别离写有数字1，2，3，4的4张卡片，从这4张卡片中随机抽取2张，则掏出的2张卡片上的数字之和为奇数的概率是（ ）A ．14B ．13C ．12D ．23 8. 在正四面体的6条棱中随机抽取2条，则其2条棱彼此垂直的概率为 （ ） A ．34 B ．23 C ．15 D ．13二、填空题9. 甲、乙两队进行排球决赛，此刻的情形是甲队只要再赢一局就获冠军，乙队需要再赢两局才能得冠军，若两队胜每局的概率相同，则甲队取得冠军的概率为_______；10. 一个三位数字的密码键,每位上的数字都在0到9这十个数字中任选,某人忘记后一个号码,那么这人开锁时,在对好前两位数码后,随意拨动最后一个数字恰好能开锁的概率为 _11. 现有10个数，它们能组成一个以1为首项，3-为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是 ;12. 三位同窗参加跳高、跳远、铅球项目的竞赛，若每人只选择一个项目，则有且仅有两位同窗选择的项目相同的概率是 （结果用最简分数表示）.三、解答题13. 某学校数学爱好小组有10名学生，其中有4名女同窗；英语爱好小组有5名学生，其中有3名女学生，现采纳分层抽样方式（层内采纳不放回简单随机抽样）从数学爱好小组、英语爱好小组中共抽取3名学生参加科技节活动。

第二十一天 完成日期 月 日 星期学法指导：综合应用等比和等差数列知识解题一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1．已知数列}{n a 的前n 项和)0(1≠-=a a S n n ，则数列}{n a（ ）A ．一定是等差数列B ．一定是等比数列C ．或者是等差数列，或者是等比数列D ．既不可能是等差数列，也不可能是等比数列2. 已知数列{}n a 是公比为q 的等比数列，且1a ，3a ，2a 成等差数列，则q ＝ （ ）A ．1或12-B ．1C ．12- D ．－23．已知等比数列}{n a 中，有71134a a a =，}{n b 是等差数列，且77a b =，则=+95b b （ ）A. 2B.4C.8D.164．若三个实数c b a ,,成等差数列，b a c ,,成等比数列，且102=++c b a ，则a 的值为（ ）A. 4B. 2C. -2D. -5或525．已知{}n a 为等比数列，n S 是它的前n 项和。

若2312a a a ⋅=， 且4a 与27a 的等差中项为54，则5S =（ ）A ．35B.33C.31D.296. 设n S 是公差不为0的等差数列{}n a 的前n 项和，且421,,S S S 成等比数列，则12a a 等于（ ） A.1B. 2C. 3D. 47. 设{}n a 是等差数列. 下列结论中正确的是（ ）A ．若120a a +>，则230a a +>B ．若130a a +<，则120a a +<C ．若120a a <<，则2a D ．若10a <，则()()21230a a a a --> 8. 已知数列{}n a 为等差数列，{}n b 为等比数列，且满足：10031013a a π+=，692b b ⋅=，则1201578tan1a a b b +=+（ ）A .1B .1-CD.二．填空题9. 已知数列9,,,121a a 是等差数列，数列9,,,,1321b b b 是等比数列，则212a ab +的值为 .10. 已知函数()()()()⎩⎨⎧>≤--=-77336x ax x a x f x ，若数列{}n a 满足()n a f n =（n N *∈），且{}n a 是递增数列，则实数a 的取值范围是 ___________．11．若数列12,,,x a a y 成等差数列，12,,,x b b y 成等比数列，则21212()a a b b +的取值范围是 .12. 设n S 是数列{}n a 的前n 项和，且11a =-，11n n n a S S ++=，则n S = ．三．解答题（应写出文字说明、证明过程或演算步骤）13．有四个数，前三个数成等差数列，后三个数成等比数列，首末两项之和为37，中间两项之和为36，求这四个数。

第十一天 完成日期 月 日星期学法指导：理解三角函数的相关概念，同角三角函数的基本关系。

一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的）1. 将表的分针拨慢10分钟，则分针转过的角的弧度数是 （ ） A.3πB.6π C.-3π D.-6π 2. 已知扇形的周长是6cm ，面积是22cm ，则扇形的圆心角的弧度数是（ ）A.1B.4C.1或4D.2或43. 已知角α终边上一点P 的坐标是（2sin 2,2cos 2-)，则αsin 等于 （ ）A.2sinB.2sin -C.2cosD. 2cos -4. α是第二象限角，(P x 为其终边上一点，且cos 4x a =，则αsin 的值为 （ ）A B ．4 D 5. 若α为第二象限角，则下列各式恒小于零的是（ ） A ．ααcos sin + B ．ααsin tan + C ．1cos tan a a- D ．ααtan sin - 6. 已知αsin =55，则αα44cos sin -的值为（ ）A.53- B.51- C.51 D.537. 若βαtan ,tan 是关于x 的方程20x px q -+=的两个实根，βαtan 1,tan 1是关于方程02=+-s rx x 的两个实根，那么=rs（ ）A ．pqB ．1pqC ．2p qD ．2q p8. 若5sin 2cos -=+αα,则αtan 等于（ ） A.21 B.2 C.21- D.-2二.填空题9. 已知tan 2θ=，则22sin sin cos 2cos θθθθ+-= . 10．已知角α的终边落在直线)0(3<-=x x y 上，则=-ααααcos cos sin sin .11．若()π,0∈A ,且137cos sin =+A A ,则=-+AA A A cos 7sin 15cos 4sin 5 . 12.)2sin()2(sin )tan()2cos()cos()(sin 32πααπαππααππα--∙+∙+--∙+∙+= ．三.解答题（应写出文字说明、证明过程或演算步骤） 13. 已知a a +-=11sin θ,aa +-=113cos θ,若θ是第二象限角，求实数a 的值.14.已知31sin sin =+y x ，求x y 2cos sin -的最大值.15.设函数)(x f 满足)2|(|,cos sin 4)(sin 3)sin (π≤=+-x x x x f x f .（1）求函数)(x f 的解析式； （2）求)(x f 的值域；（3）设函数2()2cos sin g x x x m =++,对任意R x ∈0,有0()()g x f x <恒成立,试求实数m 的取值范围.【链接高考】16. 【2015高考重庆】若tan 2tan 5πα=，则3cos()10sin()5παπα-=-（ ）A 、1B 、2C 、3D 、4第十一天1.A2.C3.D4.A5.B6.A7.C8.B9. 4510．2. 11.438. 12.1 13 .9114 .9415 （1）()2f x =[1,1]x ∈- （2）[1,1]- （3）3m <- 16.C。

第十三天 完成日期 月 日 礼拜学法指导：灵活应用三角函数知识进行有关三角函数的求值等。

一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1.若21cos -=α，23sin -=β，),2(ππα∈，)2,23(ππβ∈，则=+)sin(βα （ ）A ．23B ．23-C ．1-D ．02.已知πβπα<<<<20,3sin5,54)cos(-=+βα,则=βsin（ ）A ．0B ．0或2425C ．2425D ．24253.12cos312sinππ-的值是（ ）A ．0B ．2 C D ．24.函数)(),6cos()3sin(2R x x x y ∈+--=π的最小值等于 （ ）A. 3-B.2-C.1-D.5-5.函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间是 （ ）A. ]3,0[πB. ]127,12[ππC. ]65,3[ππD. ],65[ππ 6.锐角三角形的内角A 、B 知足B AA tan 2sin 1tan =-，则有 （ ）A.0cos 2sin =-B AB.0cos 2sin =+B AC.0sin 2sin =-B AD.0sin 2sin =+B A7.函数44sin cos y x x =+的值域是（ ）A.[]0,1B. []1,1-C.13,22⎡⎤⎢⎥⎣⎦D.1,12⎡⎤⎢⎥⎣⎦8.已知1cos sin 21cos sin x xx x -+=-++，则tan x 的值为（ ）A.34B. 34- C. 43D.43-二.填空题 9.=-3512cos 342π . 10. 函数22sin cos 1sin x xyx的值域是 .11. =+++87cos 85cos 83cos 8cos 4444ππππ.12. 若θθcos sin 3=，则θθ2sin 2cos +的值等于 .三、解答题（应写出文字说明、证明进程或演算步骤） 13. 求[]0200080sin 2)10tan 31(10sin 50sin 2⋅++的值.14. 若55sin =A ,1010sin =B ,且B A ,均为钝角,求B A +的值.15. 已知αtan 、βtan 是方程0242=--x x 的两个实根，求)(sin 3)cos()sin(2)(cos 22βαβαβαβα+-++++的值.【链接高考】16. 【2015高考上海】已知函数()sin f x x =．若存在1x ，2x ，⋅⋅⋅，m x 知足120x x ≤<<⋅⋅⋅6m x π<≤，且()()()()()()1223112n n f x f x f x f x f x f x --+-+⋅⋅⋅+-=，（2m ≥，m *∈N ），则m 的最小值为 ．第十三天9.10. (14,2⎤-⎥⎦； 11. 2312. 7513. 14.47π15. 35-．。

三十一天 完成日期 月 日星期学法指导1.了解柱、锥、台、球及简单组合体的结构特征。

2.理解简单空间图形的三视图。

3.会求球、棱柱、棱锥、台的表面积和体积。

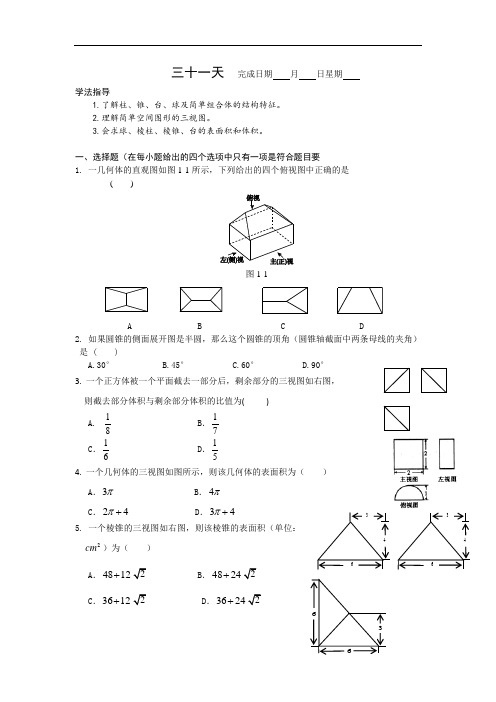
一、选择题（在每小题给出的四个选项中只有一项是符合题目要 1. 一几何体的直观图如图1-1所示，下列给出的四个俯视图中正确的是( )图1-1A B C D2. 如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角（圆锥轴截面中两条母线的夹角）是 ( )A.30°B.45°C.60°D.90° 3. 一个正方体被一个平面截去一部分后，剩余部分的三视图如右图， 则截去部分体积与剩余部分体积的比值为( )A .81 B ．71C ．61D ．514. 一个几何体的三视图如图所示，则该几何体的表面积为（ ） A ．3π B ．4π C ．24π+ D ．34π+5. 一个棱锥的三视图如右图，则该棱锥的表面积（单位：2cm ）为（ ）A ．1248+B ．2448+C ．1236+D ．2436+6.在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a 和b 的线段，则b a +的最大值为（ ）A ．B ．C ．4D ．7.棱长为1的正方体1111D C B A ABCD -的8个顶点都在球O 的表面上，FE 、分别是棱1AA 、1DD 的中点，则直线EF 被球O 截得的线段长为（ ） A.22B.1C.1+22 D.28.如图，ABC ∆为正三角形，A A '//B B '//C C '，C C '⊥平面ABC 且A A '3＝B B '23＝C C '＝AB ，则多面体C B A ABC '''-的正视图(也称主视图)是( )二、填空题9.如图所示，F E 、分别是正方体的面11A ADD 、面11B BCC 的中心，则四边形E BFD 1在该正方体的面上的正投影可能是 .（把可能的图的序号都填上）10. 现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个。

安徽省六安市舒城中学2016年高一数学暑假作业2 理第二天 完成日期 月 日 星期学法指导:1.理解和掌握函数的定义域，值域等概念；2.会求函数的解析式，定义域，值域等.一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的）1. 下列函数中，与函数x y =相同的函数是 （ ）A. 2x y x= B.=y (x )2C. lg10x y =D. 2log 2xy =2. 若2(),(1)0,(3)0,f x x bx c f f =++==则求(1)f -的值为（ ）A ．2B ．-5C ．-8D ．8 3. 图中的图象所表示的函数的解析式为 （ ）A. |1|23-=x y (20≤≤x ) B. |1|2323--=x y (20≤≤x )C. |1|23--=x y (20≤≤x )D. |1|1--=x y (20≤≤x )4. 设36log (1)(6)()31(6)x x x f x x --+>⎧=⎨-≤⎩满足8()9f n =-，则(4)f n +=( )A ．2B ．2-C ．1D ．1-5. 设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩, 2(2)(log 12)f f -+=( ) A ．3 B ．6C ．9D ．12 6. 函数)34(log 15.0-=x y 的定义域为（ ）A.（43，1） B.（43，+∞） C.（1，+∞） D.}143|{≠>x x x 且7. 已知221)1(xx x x f +=-,则=)(x f（ ）A. x x 22- B. x x 22+C. 22+xD. 22-x8. 用{}c b a ,,min 表示c b a ,,三个数中的最小值，设{}x x x f x-+=10,2,2m in )(（0x ≥）,则()f x 的最大值为（ ）A.7B.6C.5D. 4二、填空题9.已知函数ϕ(x )=)()(x g x f +,其中)(x f 是正比例函数,)(x g 是反比例函数，且ϕ(31)=16, ϕ(1)=8,则ϕ(x )=10.定义在R 上的函数)(x f 满足xy y f x f y x f 2)()()(++=+,2)1(=f ,则)3(-f = 11.若函数)1(+x f 的定义域为[0,1]，则)22(-x f 的定义域为12.设函数1()702()0xx <f x x ⎧⎪= ≥-，若1)(<a f ，则实数a 的取值范围是三、解答题（应写出文字说明、证明过程或演算步骤）13. 已知()f x 是一次函数，且满足3(1)2(1)217f x f x x +--=+，求()f x 的解析式；14.求下列函数的解析式：（1）设(cos )cos 2f x x =，求()f x 的解析式； （2）已知2(1)lg ,f x x+=求()f x 的解析式.ODCB A15. 如图，等腰梯形ABCD 内接于一个半径为r 的圆，且下底r AD 2=，如图，记腰AB 长为x ，梯形周长()y f x =.求()f x 的解析式、定义域和最大值.【链接高考】16.【2015年安徽高考】函数()()2ax bf x x c +=+的图象如图所示，则下列结论成立的是（ ）（A ）0a >，0b >，0c < （B ）0a <，0b >，0c > （C ）0a <，0b >，0c < （D ）0a <，0b <，0c <第二天1.C2.D3. B4.B5.C6.A7.C8. B9. 3x +x5; 10. 6; 11.]2,3[log 2;12. (-3,1). 13. ()27f x x =+14. (1)2()21,[1,1]f x x x =-∈-; ；)1(12lg )()2(>-=x x x f 15. 21()()5f x x r r r=--+，定义域为2)r ,x r =时有最大值5r16.C。

第三十六天 完成日期 月 日 星期学法指导:1.进一步理解空间点、线、面之间的位置关系。

2.掌握有关空间角的计算。

3.掌握线线、线面、面面关系的性质与判定。

一、选择题（在每小题给出的四个选项中只有一项是符要求的）1.过球的一条半径的中点,作垂直于该半径的平面,则所得截面面积与球的表面积的比为（ ）A.163 B.169 C.83 D.329 2.已知两个平面垂直，下列命题其中正确的个数是( )①一个平面内的已知直线必垂直于另一个平面的任意一条直线； ②一个平面内的已知直线必垂直于另一个平面的无数条直线； ③一个平面内的任一条直线必垂直于另一个平面；④过一个平面内任意一点作交线的垂线，则垂线必垂直于另一个平面.A.3B.2C.1D.0 3.如图所示，一个空间几何体的正视图、侧视图、俯视图为全等的 等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何 体的体积为（ ）A.1B.21C.31 D.614.给出下列命题：（1）直线a 与平面α不平行，则a 与平面α内的所有直线都不平行； （2）直线a 与平面α不垂直，则a 与平面α内的所有直线都不垂直； （3）异面直线a 、b 不垂直，则过a 的任何平面与b 都不垂直； （4）若直线a 和b 共面，直线b 和c 共面，则a 和c 共面. 其中错误命题的个数为( )A. 0B. 1C. 2D. 35.把半径为1的四个球垒成两层放在桌上，下层三个，上层一个，两两相切，则上层小球的球心到桌面的距离是（ ）A.13+B.1362+ C.2362+ D.1362-6.正方体的全面积为24，球O 与正方体的各棱均相切，球O 的体积是（ ）A.34π B.4π3 C.8π6 D.π3287.在正方体1111D C B A ABCD -中，O 是底面ABCD 的中心，M 、N 分别是棱1DD 、11C D 的中点，则直线OM （ ）A.和AC 、MNB.垂直于AC ，但不垂直于MNC.垂直于MN ，但不垂直于ACD.与AC 、MN8.如图，动点P 在正方体1111ABCD A B C D -的对角线1BD 上．过点P 作垂直于平面11BB D D 的直线，与正方体表面相交于M N ，．设B P x =，MN y =，则函数()y f x =的图象大致是（ ）二、填空题9.已知正四棱锥的体积为12，底面对角线的长为26，则侧面与底面所成的二面角的大小等于10.如图1，一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块，容器内盛有a 升水时，水面恰好经过正四棱锥的顶点P 。

第一天 完成日期 月 日学法指导：1.理解集合的概念，元素与集合的关系。

2.识别集合之间的基本关系，并能用venn 图来描述相关基本运算。

一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1．已知集合{}0,1,2A =，{}|,,B z z x y x A y A ==+∈∈，则B =（ ）A ．{}0,1,2,3,4B ．{}0,1,2C ．{}0,2,4D ．{}1,2 2. 已知集合M={},N x 8|N x ∈-∈则M 中元素的个数是（ ） A. 10B. 9C.8D.73. 已知集合{|},{|12},()R A x x a B x x A C B R =<=<<=U ，则实数a 的取值范围是 （ ）A.2a ≥B.2a >C.D.1a < 4．下列各组两个集合A 和B 表示同一集合的是（ ）A ．{}{}, 3.14159AB π== B ．{}(){}2,3,2,3A B ==C ．{}{}3,,,1,3A B ππ==D ．{}{}|11,,1A x x x N B =-<≤∈=5. 设全集U=R,集合)}1ln(|{},12|{)2(x y x B x A x x -==<=-，则图中阴影部分表示的集合为( ) A. {}1x |x ≥ B.{}1x |x ≤ U ABC. {}2x 1|x <≤D. {}1x 0|x ≤<6. 设集合},01|{<<-=m m P }044|{2恒成立对任意的实数x mx mx m Q <-+=则下列关系中成立的是（ ） A. P ⊆Q B. Q ⊆PC. P=QD. P ⊄Q27. {|,},()().{|3,},{|2,}.x M N M N x x M x N M N M N N M A y y x x x R B y y x R A B -=∈∉⊕=-⋃-==-∈==-∈⊕=对于集合、，定义且 设则（ ） A.]0,49(-B.)0[)49,(∞+⋃--∞，C.)0,49[-D.)0()49,(∞+⋃--∞，8. 设S 是至少含有两个元素的集合，在S 上定义了一个二元运算“*”（即对任意的,a b S ∈，对于有序元素对（a ，b ），在S 中有唯一确定的元素a*b 与之对应）．若对任意的,a b S ∈，有(*)a b a b *=，则对任意的,a b S ∈，下列等式中不恒成立的是 （ ） A ．(*)*a b a a =B ．*(*)b b b b =C ．[*(*)]*(*)a b a a b a =D ．(*)*[*(*)]a b b a b b =二、填空题9. 已知集合,1},02|{2A a x x x A ∉>+-=且则实数a 的取值范围是 10.若全集{}{}0,1,2,32U U C A ==且，则集合A 的真子集共有 个 11．已知集合{}24A x y x ==-，{}1B x a x a =≤≤+，若A B A =U ，则实数a 的取值范围为12. 设P 是一个数集，且至少含有两个数，若对任意a 、b ∈P ，都有a+b 、a-b 、ab 、ba∈P （除数b ≠0）,则称P 是一个数域.例如有理数集Q 是数域;数集F={a+b 2|a,b ∈Q}也是数域.有下列命题:①整数集是数域; ②若有理数集Q ⊆M,则数集M 必为数域; ③数域必为无限集; ④存在无穷多个数域.其中正确的命题的序号是 三、解答题（应写出文字说明、证明过程或演算步骤）13. 含有三个实数的集合可表示为{a,}1,ab，也可表示为{},0,b a ,a 2+求20162016a b +的值． 14．已知x ∈R ，集合A ＝｛023|2=+-x xx ｝，B ＝｛02|2=+-mx x x ｝，若A∩B ＝B ，求实数m 的取值范围．15．设全集U R =，已知函数()1f x x =-的定义域为集合A ，函数()()1,102xg x x ⎛⎫=-≤≤ ⎪⎝⎭的值域为集合B .（1）求()U C A B I ；（2）若{}|21C x a x a =≤≤-且B C ⊆,求实数a 的取值范围.（1）当21=a 时，求(R B)⋂A; （2）若B A ⊆,求实数a 的取值范围。

安徽省六安市舒城中学2016年高一数学暑假作业33 文第三十三天 完成日期 月 日学法指导:1.理解空间线线、线面、面面的位置关系。

2.理解空间线线、线面、面面关系的性质与判定。

一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的）1. 已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ）A ．34 B.54C.74D. 342. 如图，已知六棱锥ABCDEF P -的底面是正六边形，AB PA ABC PA 2,=⊥平面则下列结论正确的是（ ） A. AD PB ⊥B. PAB 平面PBC 平面⊥C. 直线BC ∥PAE 平面D. 直线ABC PD 与平面所成的角为45°3. 如图，正方体1111ABCD A BC D -的棱线长为1，线段11B D 上有两个点E ，F ，且22EF =，则下列结论中错误的是 （ ）A ．AC BE ⊥B ．//EF ABCD 平面C ．三棱锥A BEF -的体积为定值D ．异面直线,AE BF 所成的角为定值4. 平面六面体1111ABCD A BC D -中，既与AB 共面也与1CC 共面的棱的条数为（ ）A ．3B ．4C ．5D ．65. 已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ）A34 B54C74D346. 若正方体的棱长为2，则以该正方体各个面的中心为顶点的凸多面体的体积为（ ）A26 B 23 C 33D237. 如图，正方体1111ABCD A BC D -的棱线长为1，线段11B D 上有两个动点E ，F ，且12EF =，则下列结论中错误的是（ ） A. AC BE ⊥ B.//EF ABCD 平面C. 三棱锥A BEF -的体积为定值D. AEF BEF ∆∆的面积与的面积相等8. 正方体ABCD —1A 1B 1C 1D 的棱上到异面直线AB ，C 1C 的距离相等的点的个数为 （ ）A ．2B ．3 C. 4 D. 5二、填空题9. （国1文理）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3，则它的表面积是10.点,A B 到平面α的距离分别为4cm 和6cm ，则线段AB 的中点M 到α平面的距离为__________．11.在正三棱锥P ABC -（顶点在底面的射影是底面正三角形的中心）中，4,8AB PA ==,过A 作与,PB PC 分别交于D 和E 的截面，则截面∆ADE 的周长的最小值是 ．12. 在直三棱柱ABC －A 1B 1C 1中，底面为直角三角形，∠ACB ＝90°，AC ＝6，BC ＝CC 1＝2，P 是BC 1上一动点，则CP ＋PA 1的最小值是________． 三、解答题（应写出文字说明、证明过程或演算步骤）13. 若某几何体的三视图（单位：cm ）如图所示，求此几何体的体积14. 如图所示，三棱柱ABC ­ A 1B 1C 1中，AA 1⊥BC ，A 1B ⊥BB 1. (1)求证：A 1C ⊥CC 1；(2)若AB ＝2，AC ＝3，BC ＝7，问AA 1为何值时，三棱柱ABC ­ A 1B 1C 1体积最大，并求此最大值．15.如图在三棱柱111ABC A B C -中，1CC ⊥平面ABC ，111,1,2,A B BC BC AA AC E ⊥===、F 分别为11A C BC 的中点.（1）求证：1C F 平面EAB ； （2）求三棱锥A BCE -的体积.16 在正四棱台内，以小底为底面。

第二十三天 完成日期 月 日 星期学法指导：理解递推公式与数列通项公式关系一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的）1．已知数列{}n a 满足*111,2()n n n a a a n N +=⋅=∈，则10a =（ ） A ．64B ．32C ．16D ．82. 已知数列{}n a 满足：22111, 0, 1(*)n n n a a a a n +=>-=∈N ，那么使5n a <成立的n 的最大值为（ ）A.4B.5C.24D.25 3. 已知1112,1()n na a n N a *+==-∈，记数列{}n a 的前n 项之积为n T ，则2015T 的值为( )A ．－12B ．－1 C.12 D ．24. 在数列{}n a 中，12a =， 11ln(1)n n a a n+=++，则n a =( )A ．2ln n +B ．2(1)ln n n +-C ．2ln n n +D ．1ln n n ++ 5. 如果数列{}n a 满足122,1a a ==且1111++---=-n n n n n n n n a a a a a a a a (n ≥2),则此数列的第10项为( ) A.1021 B.921 C.101D.516. 已知数列{}n a 满足：11a =，12n n n a a a +=+，（*n N ∈），则数列{}n a 的通项公式为（ ）A ．21n n a =-B ．1122n n a -=-C.121n n a =-D.132n na =- 7. 已知数列{}n a满足112n a +=且112a =,则该数列的前 2 010项的和等于（ ） A.20153B.3 015C.1 005D.2 0108．满足*12121,log log 1()n n a a a n +==+∈N ，它的前n 项和为n S ，则满足1025n S >的最小n 值是（ ）A ．9B ．10C ．11D ．12二、填空题9．在数列{}n a 中，11a =，且对于任意自然数n ，都有1n n a a n +=+，则100a ＝ 10．在数列}{n a 中，已知11=a ，且满足11++=+n a a a nn n ，则n a =____________ 11．在数列}{n a 中，311=a ，n S 为数列}{n a 的前项和且n n a n n S )12(-=，则=n S ; 12．已知数列{}n a 满足：m a =1（m 为正整数），1,231,nn n n n a a a a a +⎧⎪=⎨⎪+⎩当为偶数时，当为奇数时。