当前位置：文档之家 › 7-2强度理论

7-2强度理论

  • 格式：ppt
  • 大小：1.01 MB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

材料力学第七章应力状态和强度理论

材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

材料力学第18讲 Chapter7-2第七章 应力状态(应力圆)

材料力学第18讲 Chapter7-2第七章 应力状态(应力圆)

x
y
2
R cos[180o
(2
20 )]
xy
x
2
y
R cos(2
20 )
O
xy
x
y
2
R(cos 2
cos 20
sin 2
sin 20 )
x
y
2
x
2
y
cos 2
xy
sin
2
D
A ( x , xy )
y R 2 20
E
C
x
B ( y , xy )
13
单元体与应力圆的对应关系
y y
y
10
a
64103 110103 3.206107 1012
219.6MPa
200
b
64103 100103 3.206107 1012
199.6MPa
10
c
64103 0 3.206107 1012
0.0MPa
120
10
c z
b a y
30
(Fs 160kN; M 64kN m)
xy
（3）以C 为圆心，AC为半径画圆
—应力圆或莫尔圆
O
xy
y
y
xy x
Ox
A ( x , xy )
y C
B ( y , xy )
x
10
3、单元体公式与应力圆的关系
以上由单元体公式
应力圆（原变换）
下面寻求由应力圆
单元体公式（逆变换）
只有这样，应力圆才能与公式等价 换句话，单元体与应力圆是否有一一对应关系？
x
x
x
0
y 1

材料力学应力和应变分析强度理论

材料力学应力和应变分析强度理论

§7–5 广义虎克定律
y
一、单拉下旳应力--应变关系
x
x
E
y
E
x
ij 0 (i,j x,y,z)
二、纯剪旳应力--应变关系
z
E
x
z
y
xy
xy
G
i 0 (i x,y,z)
z
yz zx 0
x
x
xy
x
三、复杂状态下旳应力 --- 应变关系
y
y
x
y x
z
xy
z
x
依叠加原理,得:
x
1
(MPa)
解法2—解析法：分析——建立坐标系如图
45 25 3
95
60°
i j
x
2
y
（
x
2
y
）2
2 xy
y
1
25 3 y 45MPa
° 5
0
Ox
6095MPa 6025 3MPa
yx 25 3MPa xy
x ?
x
y
2
sin 2
xy cos 2
25 3 x 45 sin 120o 25 3 cos120o
y
z
z
y
证明: 单元体平衡 M z 0
xy x
x
( xydydz)dx( yxdzdx)dy0
xy yx
五、取单元体： 例1 画出下图中旳A、B、C点旳已知单元体。
F
A
y
F x
x
A
B
C z
x B x
zx
xz
F
Mex
yx
C
xy
FP

材料力学第七章 应力状态

材料力学第七章 应力状态

主平面的方位：
tan
2a0
2 xy x
y
主应力与主平面的对应关系： max 与切应力的交点同象限
例题：一点处的平面应力状态如图所示。
已知 x 60MPa， xy 30MPa, y 40MPa, a 30。
试求（1）a 斜面上的应力； （2）主应力、主平面； （3）绘出主应力单元体。
x y cos 2a
2
x sin 2a
x
a
x y sin 2a
2
x cos 2a
300
10 30 2
10 30 cos 60020sin 600
2
2.32 MPa
300
10 30 sin 600 2
20cos 600
1.33 MPa
a
20 MPa
c
30 MPa
b
n1
y xy
a x
解：（1）a 斜面上的应力
y xy
a
x
2
y
x
2
y
cos 2a
xy
sin 2a
60 40 60 40 cos(60 ) 30sin(60 )
2
2
a x 9.02MPa
a
x
y
2
sin
2a
xy
cos
2a
60 40 sin(60 ) 30cos(60 ) 2
58.3MPa
2
1.33 MPa
300 600 x y 40 MPa
在二向应力状态下，任意两个垂直面上，其σ的和为一常数。
在二向应力状态下，任意两个垂直面上，其σ 的和为
一常数。
证明： a
x y

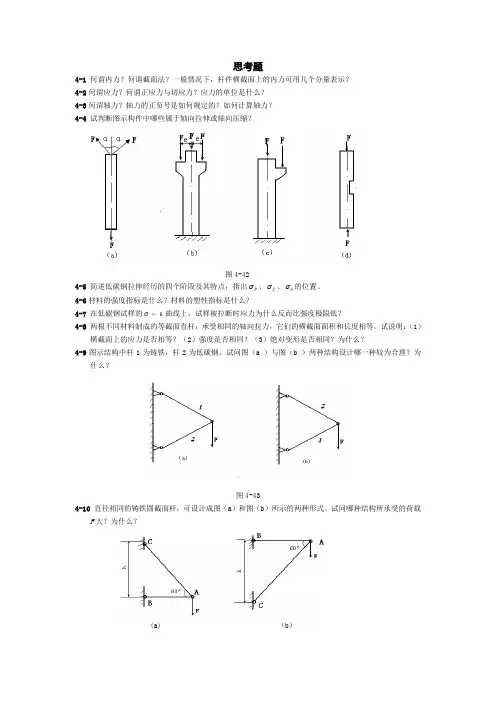
材料力学思考题2

材料力学思考题2

思考题4-1 何谓内力？何谓截面法？一般情况下，杆件横截面上的内力可用几个分量表示？4-2何谓应力？何谓正应力与切应力？应力的单位是什么？4-3何谓轴力？轴力的正负号是如何规定的？如何计算轴力？4-4 试判断图示构件中哪些属于轴向拉伸或轴向压缩？图4-424-5 简述低碳钢拉伸经历的四个阶段及其特点，指出P σ、S σ、b σ的位置。

4-6材料的强度指标是什么？材料的塑性指标是什么？4-7 在低碳钢试样的σ－ε曲线上，试样被拉断时应力为什么反而比强度极限低？4-8 两根不同材料制成的等截面直杆，承受相同的轴向拉力，它们的横截面面积和长度相等。

试说明：（1）横截面上的应力是否相等？（2）强度是否相同？（3）绝对变形是否相同？为什么？4-9图示结构中杆1为铸铁，杆2为低碳钢。

试问图（a ）与图（b ）两种结构设计哪一种较为合理？为什么？图4-434-10 直径相同的铸铁圆截面杆，可设计成图（a ）和图（b ）所示的两种形式。

试问哪种结构所承受的荷载F 大？为什么？(a) （b ）图4-444-11何谓许用应力？安全系数的确定原则是什么？何谓强度条件？利用强度条件可以解决哪些形式的强度问题？4-12一根钢筋试样，其弹性模量E = 210GPa，比例极限σp=210MPa；在轴向拉力F作用下，纵向线应变为ε=0.001 。

试求钢筋横截面上的正应力。

如果加大拉力F，试样的纵向线应变增加到ε=0.01，问此时钢筋横截面上的正应力能否由胡克定律确定，为什么？思考题5-1试指出图示各杆哪些发生扭转变形？图5-195-2轴的转速、所传递的功率与外力偶矩之间有何关系？5-3在变速器中，转速快的轴较细，而转速慢的轴较粗，这是为什么？5-4何谓扭矩？扭矩的正负号是如何规定的？如何计算扭矩？5-5圆轴扭转切应力公式是如何建立的？该公式的应用条件是什么？5-6 判断图中所示切应力分布图，哪些是错误的？图5-205-7从强度和刚度方面考虑，为什么空心圆截面轴比实心圆截面轴合理？5-8长为l、直径为d的两根由不同材料制成的圆轴，在其两端作用相同的扭转力偶矩M，试问：e（1）最大切应力τ是否相同？为什么？max（2）相对扭转角ϕ是否相同？为什么？5-9若圆轴的长度增加一倍，则扭转角将增加多少倍？若只将其直径增加一倍，则扭转角将减少到原来的几分之一？5-10若单元体的对应面上同时存在切应力和正应力，切应力互等定理是否依然成立？思考题6-1 剪力和弯矩的正负号按什么原则确定的？它与坐标的选取是否有关？6-2怎样用简单方法确定任一横截面上的剪力和弯矩？6-3在集中力和集中力偶作用处，剪力图与弯矩图有何特点？6-4 写梁的S F 、M 方程时，在何处需要分段？6-5 如何理解在集中力作用处，剪力图有突变；在集中力偶作用处，弯矩图有突变？6-6 如何建立剪力、弯矩与载荷集度间的微分关系？它们的意义是什么？在建立上述关系时，载荷集度的正负号与坐标x 的指向选取有何规定？6-7 在无载荷作用与均布载荷作用的梁段，剪力图与弯矩图各有何特点？思考题7-1直梁的弯曲正应力在横截面上是如何分布的？中性轴位于何处？如何计算最大弯曲正应力？ 7-2 矩形截面梁的高度增加一倍，梁的承载能力增加几倍？宽度增加一倍，承载能力又增加几倍？7-3 形状、尺寸、支承、载荷相同的两根梁，一根是钢梁，一根是铝梁，问二梁内力相同吗？应力分布相同吗？所产生的变形（位移）相同吗？7-4 T 形截面铸铁梁受力和弯矩图如图所示， （1）试画出C 、B 两截面上的正应力分布图； （2）最大拉应力,max t σ 和最大压应力,max c σ位于何处？图7-307-5 两梁的横截面如图所示， z 为中性轴。

材料力学 第七章 应力状态和强度理论


y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定： 1 2 3 （按代数值）
§7-3 空间应力状态
与任一截面相对应 的点，或位于应力 圆上，或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正，顺时针转为负。
tg 2a 0
2 x x
y
在主值区间，2a0有两个解，与此对应的a0也有两个解，其中落
在剪应力箭头所指象限内的解为真解，另一解舍掉。
三、应力圆
由解析法知，任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1）轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2）纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律－叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量，应用公式解题时，首先应写清已 知条件。

材料力学-第七章-强度理论

脆性断裂,最大拉应力准则
r1 = max= 1 [] 其次确定主应力
ma xx 2y 1 2 xy2 4x 2y 2.2 9 M 8 P
m inx 2y 1 2 xy2 4x 2y 3 .7M 2 P
1＝29.28MPa,2＝3.72MPa, 3＝0
r113M 0 Pa
根据常温静力拉伸和压缩试验,已建立起单向应力状态下的弹 性失效准则;
考虑安全系数后，其强度条件
根据薄壁圆筒扭转实验,可建立起纯剪应力状态下的弹性失 效准则;
考虑安全系数后，强度条件
建立常温静载复杂应力状态下的弹性失效准则: 强度理论的基本思想是:
确认引起材料失效存在共同的力学原因,提出关于这一 共同力学原因的假设;
像铸铁一类脆性材料均具有 bc bt 的性能，
可选择莫尔强度理论。
思考题:把经过冷却的钢质实心球体,放入沸腾的热油锅 中,将引起钢球的爆裂,试分析原因。
答:经过冷却的钢质实心球体,放入沸腾的热油锅中, 钢 球的外部因骤热而迅速膨胀,其内芯受拉且处于三向均 匀拉伸的应力状态因而发生脆性爆裂。
思考题: 水管在寒冬低温条件下,由于管内水结冰引起体 积膨胀,而导致水管爆裂。由作用反作用定律可知,水 管与冰块所受的压力相等,试问为什么冰不破裂,而水管 发生爆裂。
局限性:
1、未考虑 2 的影响，试验证实最大影响达15%。
2、不能解释三向均拉下可能发生断裂的现象, 此准则也称特雷斯卡（Tresca）屈服准则
4. 畸变能密度理论（第四强度理论） 材料发生塑性屈服的主要因素是 畸变能密度;
无论处于什么应力状态,只要危险点处畸变能密度达到 与材料性质有关的某一极限值,材料就发生屈服。
具有屈服极限 s
铸铁拉伸破坏

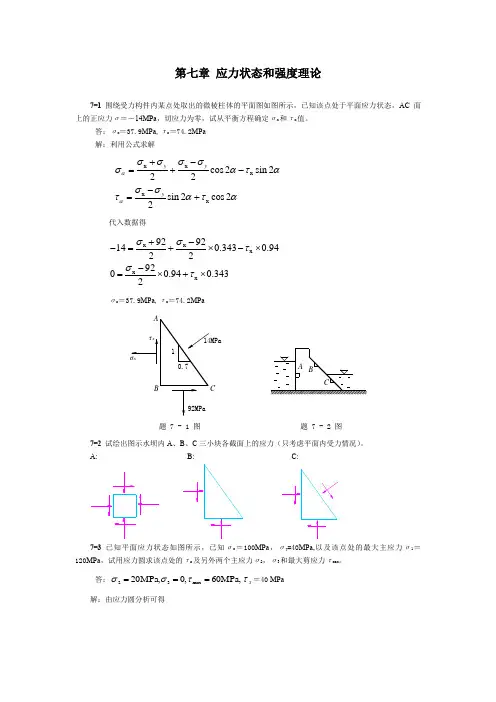
家电公司研发部资料材料力学习题答案(七)

第七章 应力状态和强度理论7-1 围绕受力构件内某点处取出的微棱柱体的平面图如图所示，已知该点处于平面应力状态，AC 面上的正应力σ＝－14MPa ，切应力为零，试从平衡方程确定σx 和τx 值。

答：σx ＝37.9MPa ,τx ＝74.2MPa 解：利用公式求解x x x x x cos 2sin 222sin 2cos 22yyyαασσσσσατασστατα+-=+--=+代入数据得x x x x x 9292140.3430.94229200.940.3432σστστ+--=+⨯-⨯-=⨯+⨯σx ＝37.9MPa ,τx ＝74.2MPa7-2 试绘出图示水坝内A 、B 、C 三小块各截面上的应力（只考虑平面内受力情况）。

A: B: C:7-3 已知平面应力状态如图所示，已知σx ＝100MPa ，σy =40MPa,以及该点处的最大主应力σ1＝120MPa ，试用应力圆求该点处的τx 及另外两个主应力σ2，σ3和最大剪应力τmax。

答：MPa,60,0MPa,20max 32===τσσx τ＝40 MPa 解：由应力圆分析可得A BC题 7 - 2 图题 7 - 1 图111(100,),(40,),(,0)x x c D D C ττσ'-x 121004070MPa221207050MPa 705020MPayc c c r r σσσσσσσ++====-=-=∴=-=-=是平面应力状态3=0σ∴222x x 13max (100)40MPa120060MPa 22c r σττσστ∴=-+⇒=--===7-4 已知平面应力状态一点处互相垂直平面上作用有拉应力90MPa 和压应力50MPa ，这些面上还有剪应力，如果最大主应力为拉应力100MPa ，试求：(1) 上述面上的切应力； (2) 此平面上另一主应力； (3) 最大切应力平面上的正应力； (4) 最大切应力。

材料力学刘鸿文第六版最新课件第七章 应力和应变分析 强度理论

不相同，此即应力的点的概念。
5
7-1 应力状态的概述
直杆拉伸斜截面上的应力
k
F
{ F
p cos cos2
k
F
k p
k
p sin cos sin sin 2
2
直杆拉伸应力分析结果表明：即 使同一点不同方向面上的应力也是各
不相同的，此即应力的面的概念。
6
7-1 应力状态的概述
点的应力状态：
虚线：主压应力迹线 实线：主拉应力迹线
思考：在钢筋混泥土梁中，钢筋怎么放置最佳。 30
内容小结：
（1）根据已知点的应力状态求任意截面的应力。 （2）根据已知点的应力状态求主应力、主平面。 （3）结合前五章内容，掌握梁在拉、压、剪、扭、弯 等状态下，求某点的应力，并计算主应力和主平面。
31
第七章 应力和应变分析
58.3MPa 22
7-3 二向应力状态分析-解析法
（2）主应力、主平面
y xy
max
x
y
2
(
x
y
)2
2 xy
2
68.3MPa
x
min
x
y
2
(
x
y
)2
2 xy
2
48.3MPa
1 68.3MPa, 2 0, 3 48.3MPa
23
7-3 二向应力状态分析-解析法
y
主平面的方位：
2
2sin cos sin2
并注意到 yx xy （切应力互等）
化简得出：
1 2
( x
y)
1 2
(
x
y ) cos 2
xy
sin
2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Szc 3 [240 20 410 10 400 200
2 0.5 10 10 398] 109 2.81 103 m 3
b 10 mm
22
(1)C2点：
Myc 690 390 s 132MPa 4 IZ 20.4 10
QSZC 670 2.05 106 67.3 MPa IZb 2.04 10
2、马里奥特关于变形过大引起破坏的论述，是第二强度理论的萌芽； 3、杜奎特（C.Duguet) 提出了最大切应力理论； 4、麦克斯威尔最早提出了最大畸变能理论（maximum distortion energy theory）；这是后来人们在他的书信出版后才知道的。
5
§8－2 四个强度理论及其相当应力
s
A
st
pD P st 4t A 5 110 0.1 18.1MPa 4 10 0.11 0.01
s 1 27.5MPa,s 2 5MPa,s 3 18.1MPa
s2 s 1 (s 2 s 3 )
27.5 0.25( 5 18.1 ) 33.3 MPa s
240 8403 230 8003 IZ 1012 12 20.4 10 4 m 4
Szc 2 [240 20 410 10 10 395
C3 C2 C1
（b）
2 0.5 10 10 398] 109 2.05 10 3 m 3
不安全。
23
s r4
1 [(s 1 s 2 )2 (s 2 s 3 )2 (s 3 s 1 )2 ] 2
1 [160.32 28.32 (28.3 160.3)2 ] 176 176 3.6 0 0 s 170
max
4、破坏形式还与温度、变形速度等有关！
15
例 8-4-1 直径为d=0.1m的圆杆受力如图,T=7kNm,P=50kN, 为铸 铁 构 件， [ s ]=40MPa, 试用第一强度理论校核杆的强 度。
T P T
A
解：危险点A的应力状态如图：
P
s
P 4 50 3 10 6.37MPa 2 A 0.1
[s y]
O2 s 3
oN
O3
O1
s 1 [ s L]
s
s
2、强度准则：
M
莫尔理论危险条件的推导
[s L ] s1 s 3 s [s y ]
3、实用范围：实用于破坏形式为屈服的构件及其拉压极限强度不等的处于 复杂应力状态的脆性材料的破坏（岩石、混凝土等）。
三、相当应力：（强度准则的统一形式）。
安全。
例 8-4-3 薄壁圆筒受最大内压时,测得 x=1.8810-4, y=7.3710-4,已知钢的E=210GPa，[s]=170MPa,泊 松比=0.3，试用第三强度理论校核其强度。
y
A
x
18
1. 已知受力状态，但是，力的大小未知； 2. 测得了α方向和与之垂直的方向的应变 α和 α+90 ，
D
A
B
F
E
C3
C2
R A 710
（a）
710
RB 710
C1
（b）
（kN） Q
120
670
x
-670 -710
解 ： 内 力 图 如 下 可 能 的 危 险 点 在 A 面上的 C2 点、 B 面上的 C1 点、 D 面上的 C3 点。
x
690 M （kNm）
870
（1）：截面图形几何性质
s s
* 1
其中，s *——相当应力。
s b , s 0.2 , s s s
n
1 s4 s 1 s 2 2 s 2 s 3 2 s 3 s 1 2 2 s s [s L ] s M 1 3
4、强度分析：选择适当的强度理论，计算相当应力，然后进行强度计算。
14
二、强度理论的选用原则：依破坏形式而定。
1、脆性材料：当最小主应力大于等于零时，使用第一理论；
当最小主应力小于零而最大主应力大于零时，使用莫尔理论。 当最大主应力小于等于零时，使用第三或第四理论。 2、塑性材料：当最小主应力大于等于零时，使用第一理论； 其他应力状态时，使用第三或第四理论。 3、简单变形时：一律用与其对应的强度准则。如扭转，都用：
M

K L
解：做莫尔理论分析图
P
s by
O2
s3

oN
O3 O1
s1 sbL
s
O2 M O1 L sin O1O2
莫尔理论危险图
1200 400 0.5 1200 400
3. 已知E、[s]、泊松比等； 1. 沿轴向取原始单元体； 并求出应力与外载的关系； 试 进 行 强 度 分 析。 2. 沿α方向取单元体，然后 90 根据广义弹性定律，求出α 方向单元体上的应力σα和 σα+90 。
3. 根据平面应力分析公式， 将α方向应力与轴向应力联系 起来，求出原始单元体上的 应力。 4. 进 行 强 度 分 析。
s3 s 1 s 3 183.1 s
s 1 183.1MPa,s 2 94.4MPa,s 3 0
s r 3 s 183.1 170 7.7 0 0 s 170
所以，此容器不满足第三强度理论。不安全
例 8-4-4 焊接钢板梁如图（a），E=210GPa， [ s ]=170MPa,[ ]=100MPa ，试用适当的强度理论校核其强度。
(3) C 3 点：
所以，不安全。
QSZC 710 2.81 106 97.8 MPa IZb 2.04 10
依简单变形（纯扭）的强度理论
[ ]
综上，整个梁不安全。
所以，安全。
25
例 8-4-5 一铸铁构件 sb L= 400MPa， sb y= 1200MPa，一平面应力状态点按 莫尔强度理论屈服时，最大切应力为450 M Pa，试求该点的主应力值。
2.1 7 ( 1 . 88 0 . 3 7 . 37 ) 10 94.4 MPa 2 1 0.3
sy
A
sx
E sy ( y x ) 2 1
2.1 7 ( 7 . 37 0 . 3 1 . 88 ) 10 183.1MPa 2 1 0.3
1 b ; ( 1 0)
1、破坏判据：
sb 1 1 s1 s 2 s 3 E E
s 1 s 2 s 3 s b
2、强度准则：
s 1 s 2 s 3 s
3、实用范围：实用于破坏形式为脆断的构件。
7
三、最大切应力（第三强度）理论：认为构件的屈服是由最大切应力引起 的。当最大切应力达到单向拉伸试验的极限切应力时，构件就破坏了。
例 8-4-2 两端封闭的铸铁薄壁圆筒，其内径为d=0.1m，壁厚 t = 1 0 m m ， 受 力 如 图 , 内 压 p = 5 M P a , P = 1 0 0 k N , [s]=40MPa,泊松比=0.25，试用第二强度理论校核其强度。
解：危险点A的应力状态如图
A
pD 5 110 s 27.5 MPa 2t 2 10

3、实用范围：实用于破坏形式为屈服的构件。
§8－3 莫尔强度理论及其相当应力
莫尔认为：最大切应力是使 物体破坏的主要因素，但滑 移面上的摩擦力也不可忽略 （莫尔摩擦定律）。综合最 大切应力及最大正应力的因 素，莫尔得出了他自己的强 度理论。
¢ Í ° Ð • ª ¶ Ä û (O.Mohr),1835« ¡ 1918
max s
max s1 s 3
2
ss
2
s
1、破坏判据： 2、强度准则：
s1 s 3 s s
s 1 s 3 s
3、实用范围：实用于破坏形式为屈服的构件。
8
四、形状改变比能（第四强度）理论：认为构件的屈服是由形状改变比能 引起的。当形状改变比能达到单向拉伸试验屈服时形状改变比能时，构件 就破坏了。
所以，安全。
24
(2) C 1 点：
Myc 870 420 s 179MPa 4 IZ 20.4 10
s 1 179MPa,s 2 0,s 3 0 依简单变形（单拉）的强度理论
s 1 s 179 170 s 1 179s , 5.3 0 0 s 170
ux max uxs
ux
1 6E
s
2
1
s 2 s 2 s 3 s 3 s 1
2 2
2

s
1、破坏判据：
1 2
s
1
s 2 s 2 s 3 s 3 s 1
2
2
s

2、强度准则
1 s 1 s 2 2 s 2 s 3 2 s 3 s 1 2 s 2
[s y ]
s s1 s 2 s 1 s 2 s 3 s 3 s1 s 3
13
§8－4 强度理论的应用
一、强度计算的步骤： 1、外力分析：确定所需的外力值。
2、内力分析：画内力图，确定可能的危险面。
3、应力分析：画危面应力分布图，确定危险点并画出单元体，求主应力。
A
s
T 16 7000 35.7 MPa 3 Wn 0.1
s1
2
s
2