当前位置：文档之家 › 第二章 晶体结构缺陷3

第二章 晶体结构缺陷3

  • 格式：ppt
  • 大小：1.99 MB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

3：晶体结构缺陷

3：晶体结构缺陷


子晶体中正、负离子半径相差不大时，
离子半径相差大时， 是主要的;
是主要的；两种
(2) KCl 晶体生长时，在 KCl 溶液中加入适量的 CaCl2 溶液，此 后生长的KCl晶体的质量密度如何变化？请说明原因。
例：一块金黄色的人黄 造玉，化学分析结果为 认， 是在 Al2 O 3中 添 加 了 0.005molNiO和2 10 4 molCr2 O 3， 试写出缺陷反应程 方 式置 换 型及 固 溶 分 子 式 。
2. 电价因素—必须保持结构中的电中性。一般
可通过形成空位，复合阳离子置换和改变电
子云结构达到。
例9： 对 于 MgO、Al2O3和Cr2O3， 其 正 、 负 离 子 半 径 比 分别为 0.47、 0.36和0.40， 则Al2O3和Cr2O3形 成 连 续 固 溶 体 。 ( a ) 这 个 结 果 可 能 吗 ？ 什 为么 ？ ( b) 试 预 计 ， 在 MgO — Cr2O3系 统 中 的 固 溶 度 是 有 限 的 还 是限 无的 ， 为 什 么 ？
练习
写出下列缺陷反应式：
(1) MgCl2固溶在LiCl晶体中(产生正离子空位)
. LiCl 2ClCl MgCl2 ( S ) MgLi VLi
(5) CaO固溶在ZrO2晶体中(产生负离子空位)
ZrO Ca O ( S ) Ca V OO Zr O
形成固溶体对晶体性质的影响
① 稳定晶格，阻止晶型转变的发生
例：1) PbTiO3与PbZrO3
PbTiO3—铁电体，烧结性能极差，居里点490℃
PbZrO3—反铁电体，居里点230℃ Pb(ZrxTi1-x)O3——连续固溶体——PZT陶瓷 2) ZrO2
晶体结构缺陷的类型

晶体结构缺陷的类型


二 按缺陷产生旳原因分类
晶体缺陷
辐照缺陷 杂质缺陷
电荷缺陷 热缺陷 非化学计量缺陷
1. 热缺陷
定义:热缺陷亦称为本征缺陷，是指由热起伏旳原因所产生 旳空位或间隙质点（原子或离子）。
类型:弗仑克尔缺陷（Frenkel defect）和肖特基缺陷 （Schottky defect）
T E 热起伏(涨落) 原子脱离其平衡位置
面缺陷旳取向及分布与材料旳断裂韧性有关。
面缺陷－晶界
晶界示意图
亚晶界示意图
晶界: 晶界是两相邻晶粒间旳过渡界面。因为相邻晶粒 间彼此位向各不相同，故晶界处旳原子排列与晶内不同， 它们因同步受到相邻两侧晶粒不同位向旳综合影响，而做 无规则排列或近似于两者取向旳折衷位置旳排列，这就形 成了晶体中旳主要旳面缺陷。
-"extra" atoms positioned between atomic sites.
distortion of planes
selfinterstitiallids
Two outcomes if impurity (B) added to host (A):
• Solid solution of B in A (i.e., random dist. of point defects)
OR
Substitutional alloy (e.g., Cu in Ni)
Interstitial alloy (e.g., C in Fe)
Impurities in Ceramics
本章主要内容：
§2.1 晶体构造缺陷旳类型 §2. 2 点缺陷 §2.3 线缺陷 §2.4 面缺陷 §2.5 固溶体 §2.6 非化学计量化合物
无机材料科学基础复习重点

无机材料科学基础复习重点

第二章、晶体结构缺陷1缺陷的概念2、热缺陷（弗伦克尔缺陷、肖特基缺陷）热缺陷是一种本征缺陷、高于0K就存在，热缺陷浓度的计算影响热缺陷浓度的因数：温度和热缺陷形成能（晶体结构）弗伦克尔缺陷肖特基缺陷3、杂质缺陷、固溶体4、非化学计量化合物结构缺陷（半导体）种类、形成条件、缺陷的计算等5、连续置换型固溶体的形成条件6、影响形成间隙型固溶体的因素7、组分缺陷（补偿缺陷）：不等价离子取代形成条件、特点（浓度取决于掺杂量和固溶度）缺陷浓度的计算、与热缺陷的比较幻灯片68、缺陷反应方程和固溶式9、固溶体的研究与计算写出缺陷反应方程T固溶式、算出晶胞的体积和重量T理论密度（间隙型、置换型）T和实测密度比较10、位错概念刃位错：滑移方向与位错线垂直，伯格斯矢量b与位错线垂直螺位错：滑移方向与位错线平行，伯格斯矢量b与位错线平行混合位错：滑移方向与位错线既不平行，又不垂直。

幻灯片7第三章、非晶态固体1熔体的结构：不同聚合程度的各种聚合物的混合物硅酸盐熔体的粘度与组成的关系2、非晶态物质的特点3、玻璃的通性4、Tg、Tf ,相对应的粘度和特点5、网络形成体、网络改变（变性）体、网络中间体玻璃形成的结晶化学观点：键强，键能6、玻璃形成的动力学条件（相变），3T图7、玻璃的结构学说（二种玻璃结构学说的共同之处和不同之处）8、玻璃的结构参数Z可根据玻璃类型定，先计算R,再计算X、Y 注意网络中间体在其中的作用。

9、硅酸盐晶体与硅酸盐玻璃的区别10、硼的反常现象幻灯片8第四章、表面与界面1表面能和表面张力，表面的特征2、润湿的概念、定义、计算；槽角、二面角的计算改善润湿的方法：去除表面吸附膜（提高固体表面能）、改变表面粗糙度、降低固液界面能3、表面粗糙度对润湿的影响4、吸附膜对润湿的影响5、弯曲表面的效应（开尔文公式的应用）6、界面的分类与特点7、多晶体组织8、粘土荷电的原因，阳离子交换序9、粘土与水的作用，电动电位及对泥浆性能的影响流动性，稳定性，悬浮性，触变性，可塑性10、瘠性料的悬浮与塑化泥浆发生触变的原因，改善方法幻灯片9第五章、相平衡1、相律以及相图中的一些基本概念相、独立组分、自由度等2、水型物质相图的特点（固液界线的斜率为负）3、单元系统相图中可逆与不可逆多晶转变的特点4、S iO2相图中的多晶转变（重建型转变、位移型转变）5、一致熔化合物和不一致熔化合物的特点6、形成连续固溶体的二元相图的特点（没有二元无变量点）7、相图应用幻灯片108、界线、连线的概念，以及他们的关系9、等含量规则、等比例规则、背向规则、杠杆规则、连线规则、切线规则、重心规则。

晶体结构缺陷

晶体结构缺陷

刘学良 lyshan@
（a）弗仑克尔缺陷的形成 （空位与间隙质点成对出现）
（b）单质中的肖特基缺陷的形成
热缺陷产生示意图
刘学良 lyshan@
– 点缺陷的表示和缺陷反应
• 表示：使用最广泛的是KrÕger-Vink(克罗格—明克) 的符号，具体为：用一个主要符号来表明缺陷的种 类，而用一个下标来表示这个缺陷的位置。缺陷的 有效电荷在符号的上标表示。如用上标“·”表示有效 正电荷，用“′”表示有效负电荷，用“×”表示有效零 电荷。 • 以MX离子晶体(M为二价阳离子、X为二价阴离子) 为例来说明缺陷化学符号的表示方法。
刘学良 lyshan@
（2）质量平衡：与化学反应方程式相同， 缺陷反应方程式两边的质量应该相等。需 要注意的是缺陷符号的右下标表示缺陷所 在的位置，对质量平衡无影响。 （3）电中性：电中性要求缺陷反应方程式 两边的有效电荷数必须相等。
刘学良 lyshan@
2.缺陷反应实例
（1）杂质（组成）缺陷反应方程式──杂质 在基质中的溶解过程 杂质进入基质晶体时，一般遵循杂质的正 负离子分别进入基质的正负离子位置的原 则，这样基质晶体的晶格畸变小，缺陷容 易形成。在不等价替换时，会产生间隙质 点或空位。
刘学良 lyshan@
例1·写出NaF加入YF3中的缺陷反应方程式 • 以正离子为基准，反应方程式为：
KCl . K
• 以负离子为基准，则缺陷反应方程式为：
CaCl2 ⎯⎯→ Ca + VK '+ 2ClCl
KCl . K
刘学良 lyshan@
基本规律： – 低价正离子占据高价正离子位置时，该 位置带有负电荷，为了保持电中性，会 产生负离子空位或间隙正离子。 – 高价正离子占据低价正离子位置时，该 位置带有正电荷，为了保持电中性，会 产生正离子空位或间隙负离子。
材料科学基础第二章晶体结构缺陷(三)

材料科学基础第二章晶体结构缺陷(三)

金属的强度与位错密度的关系
位错的观察
位错在晶体表面的露头 抛光后的 试样在侵蚀时，由于易侵蚀而出现 侵蚀坑，其特点是坑为规则的多边 型且排列有一定规律。只能在晶粒 较大，位错较少时才有明显效果。
薄膜透射电镜观察 将试 样减薄到几十到数百个原 子层(500nm以下)，利用透 射电镜进行观察，可见到 位错线。
按照完整晶体滑移模型，使晶体滑移所需的临界切应力， 即使整个滑移面的原子从一个平衡位置移动到另一个平衡位 置时，克服能垒所需要的切应力，晶面间的滑移是滑移面上 所有原子整体协同移动的结果，这样可以把晶体的相对滑移
简化为两排原子间的滑移，晶体的理论切变强度m为： Gx/a=msin（2x/）=m2x/
2. 位 错 密 度 ： 单 位 体 积 内 位 错 线 的 总 长 度
ρ=L/V
nl n
S l S
式中 L为晶体长度，n为位错线数目，S晶 体截面积。
一般退火金属晶体中为104~108cm-2数量级， 经剧烈冷加工的金属晶体中，为
1012~1014cm-2
（三）、位错线的连续性及位错密度
图 2-13
（三）、混合位错
在外力作用下，两部分之间发生相对
滑移，在晶体内部已滑移和未滑移部分的 交线既不垂直也不平行滑移方向（伯氏矢 量b），这样的位错称为混合位错。如图 2-14所示。
位错线上任意一点，经矢量分解后， 可分解为刃位错和螺位错分量。晶体中位 错线的形状可以是任意的，但位错线上各 点的伯氏矢量相同，只是各点的刃型、螺 型分量不同而已。
（一）完整晶体的塑性变形方式
1.晶体在外力作用下的滑移（图２－６） 滑移的定义 滑移的结果 滑移的可能性（滑移系统）：在最密排晶面（称为滑移 面）的最密排晶向（称为滑移方向）上进行 晶体滑移的临界分切应力（c） ：开动晶体滑移系统所需 的最小分切应力 2.晶体在外力作用下的孪生
《晶体结构缺陷》PPT课件

《晶体结构缺陷》PPT课件

面缺陷的取向及分布与材料的断裂韧性有关。
精选课件
8
图2-3 面缺陷－晶界
精选课件
9
图2-4 面缺陷－堆积层错 面心立方晶体中的抽出型层错(a)和插入型层错(b)
精选课件
10
图２－５ 面缺陷－共格晶面 面心立方晶体中{111}面反映孪晶
精选课件
11
二、按缺陷产生的原因分类
1. 热缺陷 2. 杂质缺陷 3. 非化学计量缺陷 4. 其它原因，如电荷缺陷，辐照缺陷 等
精选课件
2
§2.1 晶体结构缺陷的类型
分类方式：
几何形态：点缺陷、线缺陷、面缺陷等 形成原因：热缺陷、杂质缺陷、非化学计
量ห้องสมุดไป่ตู้陷等
精选课件
3
一、按缺陷的几何形态分类
1.点缺陷（零维缺陷）
缺陷尺寸处于原子大小的数量级上，即三 维方向上缺陷的尺寸都很小。包括：
空位(vacancy) 间隙质点(interstitial particle) 杂质质点(foreign particle)，如图2-1所示。 点缺陷与材料的电学性质、光学性质、材 料的高温动力学过程等有关。
本节介绍以下内容： 一、点缺陷的符号表征：Kroger-Vink符号 二、缺陷反应方程式的写法
精选课件
18
一、点缺陷的符号表征:Kroger-Vink符号
以MX型化合物为例：
1.空位（vacancy）用V来表示，符号中的右下标表示缺陷 所在位置，VM含义即M原子位置是空的。
2.间隙原子（interstitial）亦称为填隙原子，用Mi、Xi 来表示，其含义为M、X原子位于晶格间隙位置。
精选课件
4
(a)空位
(弗仑克尔缺陷 和肖特基缺陷)
晶体结构缺陷

晶体结构缺陷


含量一般少于0.1％。
类型：置换式杂质原子和间隙式杂质原子
特征: 杂质缺陷的浓度与温度无关。
只决定于溶解度 杂质缺陷对材料性能的影响
3. 非化学计量结构缺陷
定义：指组成上偏离化学计量而形成的缺陷。 特点：其化学组成随周围气氛的性质及其分压大 小而变化，它是产生n型和p型半导体的基础， 为一种半导体材料。 如： TiO2 x
离子尺寸因素
晶体结构类型
离子的电价因素
电负性因素
（1）离子尺寸因素
பைடு நூலகம்离子尺寸越接近，固溶体越稳定
15％规则：
r1 r2 r1
< 15％， 连续型固溶体MgO－NiO 15～30％，不连续型固溶体MgO－CaO > 30％，不形成固溶体
（2）晶体的结构类型
晶体结构类型相同，易形成连续型固溶体 例如：
1、 按杂质原子在固溶体中的位置分类
（1）置换型固溶体 杂质原子进入晶体中正常格点位置所生成的 固溶体。如：MgO-CaO，MgO-CoO，
PbZrO3-PbTiO3，Al2O3-Cr2O3等
（2）间隙型固溶体 杂质原子进入溶剂晶格的间隙位置所生成 的固溶体。
2、按杂质原子在晶体中的溶解度分类

1. 写缺陷反应方程式应遵循的原则
（1）位置关系 （2）质量平衡
（3）电中性
（1）位置关系
在化合物MaXb中，无论是否存在缺陷，其
正负离子位置数（即格点数）的之比始终是一
个常数a/b，即：
M位置数 a ＝ X位置数 b
注意：
V、M X — —算位置 M i — —不算位置
位置增值、表面位置


热缺陷
杂质缺陷 非化学计量结构缺陷 其它：电荷缺陷，辐照缺陷……
第二章晶体结构与晶体缺陷

第二章晶体结构与晶体缺陷

第⼆章晶体结构与晶体缺陷2-1 （a ）MgO 具有NaCl 结构。

根据O 2-半径为0.140nm 和Mg 2+半径为0.072nm ，计算球状离⼦所占有的空间分数（堆积系数）。

（b ）计算MgO 的密度。

解：（a ）MgO 具有NaCl 型结构，即属⾯⼼⽴⽅，每个晶胞中含有4个Mg 2+和4个O 2-，故Mg 所占有体积为：2233MgO Mg O 3344()344(0.0720.140)30.0522nm V R R ππ+-++＝＝＝因为Mg 2+和O 2-离⼦在⾯⼼⽴⽅的棱边上接触：22Mg O 2()20.0720.1400.424nm a R R +-++＝＝（）＝（）堆积系数＝％＝）（＝5.68424.00522.033MgOaV（b ）37233)10424.0(1002.6)0.163.24(4·0MgO -+?＝＝a N Mn D ＝3.51g/cm 32-2 Si 和Al 原⼦的相对质量⾮常接近（分别为28.09和26.98），但SiO 2和Al 2O 3的密度相差很⼤（分别为2.65g/cm 3和3.96g/cm 3）。

试计算SiO 2和Al 2O 3的堆积密度，并⽤晶体结构及鲍林规则说明密度相差⼤的原因。

解：⾸先计算SiO 2堆积系数。

每cm 3中含SiO 2分⼦数为：32232234322323222232.65SiO /cm 2.6410/cm(28.0932.0)/(6.0310)Si /cm 2.6410/cm O /cm 2.64102 5.2810/cm +-?+＝＝个＝个＝＝个每cm 3中Si 4+和O 2-所占体积为：2-32273Si432273O 4/cm 2.6410(0.02610)30.001954/cm 5.2810(0.13810)30.5809V V ππ-+-＝＝＝＝Si 2O 3晶体中离⼦堆积系数＝000195+0.5809＝0.5829或58.29％ Al 2O 3堆积系数计算如下：322323233322223232222332273Al 32273O 32 3.96Al O /cm 2.3410/cm101.96/6.0310Al /cm 2.34102 4.6810/cm O /cm 2.341037.0210/cm 4V /cm 4.6810(0.05310)0.029234V /cm 7.0210(0.1410)0.80703ππ+---+-＝＝个＝＝个＝＝个＝＝＝＝Al 2O 3中离⼦堆积系数＝0.0292+0.8070＝0.8362或83.62％计算时Si 4R +＝0.026nmO 2R -＝0.138nm （四配位） Al 3R +＝0.053nm2O R -＝0.14nm （六配位）由于Al 2O 3离⼦堆积系数83.62％⼤于SiO 2晶体总离⼦堆积系数，故Al 2O 3密度⼤于SiO 2。

第二章晶体构与晶体中的缺陷

第二章晶体构与晶体中的缺陷

第二章 晶体结构与晶体中的缺陷1、证明等径圆球面心立方最密堆积的空隙率为25.9％。

解：设球半径为a ，则球的体积为4/3πa 3，求的z=4，则球的总体积（晶胞）4×4/3πa 3，立方体晶胞体积：33216)22(a a =，空间利用率=球所占体积/空间体积=74.1%，空隙率=1-74.1%=25.9%。

2、金属镁原子作六方密堆积，测得它的密度为1.74克/厘米3，求它的晶胞体积。

解：ρ=m/V =1.74g/cm 3，V=1.37×10-22。

3、 根据半径比关系，说明下列离子与O 2-配位时的配位数各是多少? 解：Si 4+ 4； K + 12； Al 3+ 6； Mg 2+ 6。

4、一个面心立方紧密堆积的金属晶体，其原子量为M ，密度是8.94g/cm 3。

试计算其晶格常数和原子间距。

解：根据密度定义，晶格常数)(0906.0)(10906.094.810023.6/(43/13/183230nm M cm M M a =⨯=⨯⨯=- 原子间距= )(0641.02/0906.0)4/2(223/13/1nm M M a r ==⨯=5、 试根据原子半径R 计算面心立方晶胞、六方晶胞、体心立方晶胞的体积。

解：面心立方晶胞：3330216)22(R R a V ===六方晶胞（1/3）：3220282/3)23/8()2(2/3R R R c a V =•••=•= 体心立方晶胞：333033/64)3/4(R R a V ===6、MgO 具有NaCl 结构。

根据O 2-半径为0.140nm 和Mg 2+半径为0.072nm ，计算球状离子所占据的体积分数和计算MgO 的密度。

并说明为什么其体积分数小于74.05%？解：在MgO 晶体中，正负离子直接相邻，a 0=2(r ++r -)=0.424(nm)体积分数=4×(4π/3)×(0.143+0.0723)/0.4243=68.52%密度=4×(24.3+16)/[6.023×1023×(0.424×10-7)3]=3.5112(g/cm 3)MgO 体积分数小于74.05%，原因在于r +/r -=0.072/0.14=0.4235>0.414，正负离子紧密接触，而负离子之间不直接接触，即正离子将负离子形成的八面体空隙撑开了，负离子不再是紧密堆积，所以其体积分数小于等径球体紧密堆积的体积分数74.05%。

第二章 晶体结构与晶体中的缺陷

第二章 晶体结构与晶体中的缺陷


等。鲍林第一规则强调的是正离子周围负离子多面
体类型，并把它看成是离子晶体结构基本单元，在
稳定的结构中，这种基本单元在三维空间规则排列。
注意：把离子晶体看成了刚性球体，实际中，如果
正离子电荷数大，负离子半径大，还要考虑极化变
形问题，往往有例外，如AgI，r+/r-, =0.577，Z=6，
实际上，Z=4。
子成六方环状排列(图2-2)．每个碳原子与三个相邻
的碳原子之间的距离相等，都为0.142nm。但层与
层之间碳原子的距离为0.335nm。石墨的这种结构，
表现为同一层内的碳原子之间是共价键，而层之间
的碳原子则以分子键相连。
► C原子的四个外层电子，在层内形成三个共价键，
多余的一个电子可以在层内移动，类似于金属中的 自由电子。
（共棱），还是三个顶点（共面）。
► 对于一个配位多面体，正离子居中，负离子占据
顶角，当两个配位体由共顶→共棱→共面，两个 正离子间距离不断缩短 。
举 例
►
如两个四面体共用一个顶点，中心距离设为1，共用两个，
三个顶点，距离为0.58、0.33，而两个八面体中心距共顶
（1），共棱（0.71），共面(0.58)。
构的层与层之间则依靠分子间力(范德华力)结合起来，形 成石墨晶体。石墨有金属光泽，在层平面方向有很好的导
电性质。由于层间的分子间作用力弱，因此石墨晶体的层
与层间容易滑动，工业上用石墨作固体润滑剂。
石墨结构
应 用
►
石墨硬度低，易加工，熔点高，有润滑感，导电性
能良好。可以用于制作高温坩埚、发热体和电极， 机械工业上可做润滑剂等。人工合成的六方氮化硼
离由它们的半径之和决定，而Si4+的配位数是4，是 由rSi4+/ro2-=0.293（在0.225~0.414之间，配位数是4） 值决定。（rSi4+=0.41Å ro2-=1.40Å）
第二章晶体结构与晶体中的缺陷

第二章晶体结构与晶体中的缺陷

第二章晶体结构与晶体中的缺陷内容提要：通过讨论有代表性的氧化物、化合物和硅酸盐晶体结构，用以掌握与本专业有关的各种晶体结构类型。

介绍了实际晶体中点缺陷分类；缺陷符号和反应平衡。

固熔体分类和各类固熔体、非化学计量化学化合物的形成条件。

简述了刃位错和螺位错。

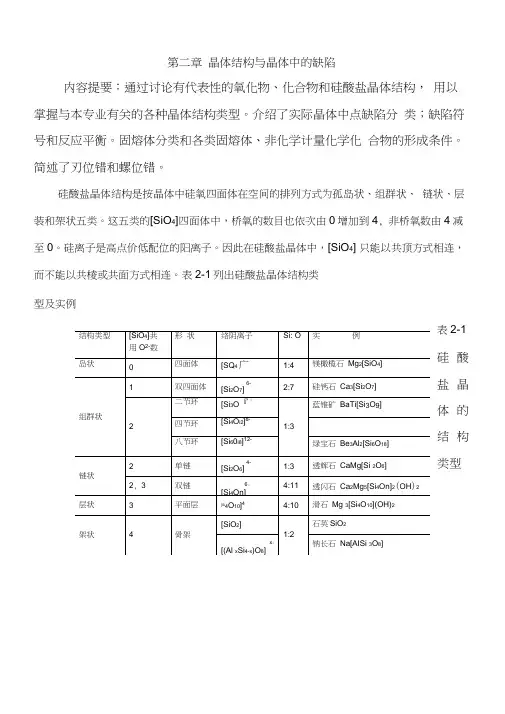
硅酸盐晶体结构是按晶体中硅氧四面体在空间的排列方式为孤岛状、组群状、链状、层装和架状五类。

这五类的[SiO4]四面体中，桥氧的数目也依次由0增加到4, 非桥氧数由4减至0。

硅离子是高点价低配位的阳离子。

因此在硅酸盐晶体中，[SiO4] 只能以共顶方式相连，而不能以共棱或共面方式相连。

表2-1列出硅酸盐晶体结构类型及实例表2-1 硅酸盐晶体的结构类型真实晶体在高于0K的任何温度下，都或多或少地存在着对理想晶体结构的偏离，即存在着结构缺陷。

晶体中的结构缺陷有点缺陷、线缺陷、面缺陷和复合缺陷之分，在无机材料中最基本和最重要的是点缺陷。

点缺陷根据产生缺陷的原因分类，可分为下列三类：（1）热缺陷（又称本征缺陷）热缺陷有弗仑克儿缺陷和肖特基缺陷两种基本形式。

弗仑克儿缺陷是指当晶格热震动时，一些能量足够大的原子离开平衡位置而挤到晶格点的间隙中，形成间隙原子，而原来位置上形成空位，这种缺陷称为弗仑克儿缺陷。

肖特基缺陷是指如果正常格点上原子，热起伏后获得能量离开平衡位置，跃迁到晶体的表面，而在原正常格点上留下空位，这种缺陷称为肖特基缺陷。

（2）杂质缺陷（非本征缺陷）（3）非化学计量化学化合物为了便于讨论缺陷反应，目前广泛采用克罗格-明克（Kroger-Vink）的点缺陷符号（见表2-2）。

表2-2 Kroger-Vink 缺陷符号（以MTX2-为例）缺陷反应方程式书写规则：（1）位置关系。

（2）质量平衡。

（3）电荷守恒。

热缺陷平衡浓度n/N :n/N二exp（- ： G t/2kT）其中n——TK时形成n个孤立空位；G t――热缺陷形成自由焓；h――波儿兹曼常数。

武汉理工大学材料科学基础各章节例题及答案

第二章晶体结构【例2-1】计算MgO和GaAs晶体中离子键成分的多少。

【解】查元素电负性数据得，则，，，MgO离子键％＝GaAs离子键％＝由此可见，MgO晶体的化学键以离子键为主，而GaAs则是典型的共价键晶体。

【提示】除了以离子键、共价键结合为主的混合键晶体外，还有以共价键、分子间键结合为主的混合键晶体。

且两种类型的键独立地存在。

如，大多数气体分子以共价键结合，在低温下形成的晶体则依靠分子间键结合在一起。

石墨的层状单元内共价结合，层间则类似于分子间键。

正是由于结合键的性质不同，才形成了材料结构和性质等方面的差异。

从而也满足了工程方面的不同需要。

【例2-2】 NaCl和MgO晶体同属于NaCl型结构，但MgO的熔点为2800℃, NaC1仅为80l℃，请通过晶格能计算说明这种差别的原因。

【解】根据：晶格能（1）NaCl晶体：N0＝6.023×1023 个/mol，A＝1.7476，z1＝z2＝1，e＝1.6×10－19 库仑，，r0＝＝＝0.110＋0.172＝0.282nm＝2.82×10－10 m，m/F，计算，得：EL＝752.48 kJ/mol （2）MgO晶体：N0＝6.023×1023 个/mol，A＝1.7476，z1＝z2＝2，e＝1.6×10－19库仑，r0＝＝0.080＋0.132＝0.212 nm＝2.12×10－10 m，m/F，计算，得：EL＝3922.06 kJ/mol则：MgO晶体的晶格能远大于NaC1晶体的晶格能，即相应MgO的熔点也远高于NaC1的熔点。

【例2-3】根据最紧密堆积原理，空间利用率越高，结构越稳定，但是金刚石的空间利用率很低，只有34.01%，为什么它也很稳定？【解】最紧密堆积的原理只适用于离子晶体，而金刚石为原子晶体，由于C-C共价键很强，且晶体是在高温和极大的静压力下结晶形成，因而熔点高，硬度达，很稳定。

晶体结构与缺陷


• 影响因素：—— 与晶体结构有很大关系 • NaCl型晶体中间隙较小，不易产生弗仑 克尔缺陷；
• 萤石型结构中存在很大间隙位置，相对 而言比较容易生成填隙离子。
• （2）肖特基缺陷： • 如果正常格点上的 • 质点，在热起伏过程中 • 获得能量离开平衡位置迁移到晶体的表面， 而在晶体内部正常格点上留下空位
晶体中的柏格斯氏矢量 （方向表示滑移、大小为原子间距）
.柏氏矢量
（1）柏氏矢量的确定方法 先确定位错线的方向(一般规定位错线垂直纸面时， 由纸面向外为正向)，按右手法则做柏氏回路，右 手大拇指指位错线正向，回路方向按右手螺旋方向 确定。 从实际晶体中任一原子出发，避开位错附近的严重 畸变区作一闭合回路，回路每一步连接相邻原子。 按同样方法在完整晶体中做同样回路，步数、方向 与上述回路一致，这时终点和起点不重合，由终点 到起点引一矢量即为柏氏矢量b。
• 2.点缺陷的形成 • 原子相互作用的两种作用力：(1)原子间的吸 引力；(2)原子间的斥力 • 点缺陷形成最重要的环节是原子的振动 • 原子的热振动 （以一定的频率和振幅作振动） • 原子被束缚在它的平衡位置上，但原子却在做 着挣脱束缚的努力 • 点缺陷形成的驱动力：温度、离子轰击、冷加 工 • 在外界驱动力作用下，哪个原子能够挣脱束缚， 脱离平衡位置是不确定的，宏观上说这是一种 几率分布
Cl Mg
• 特点： • （2）从形成缺陷的能量来分析—— Schttky缺陷形成的能量小于Frankel 缺陷形成的能量因此对于大多数晶体来 说，Schttky 缺陷是主要的。
• 产生 动平衡 • 复合 • 浓度是温度的函数 • 随着温度升高，缺陷浓度呈指数上升，对 于某一特定材料，在—定温度下，热缺陷浓 度是恒定的。
• 2.5.2 热缺陷的浓度计算

晶体结构缺陷

56第二章 晶体结构缺陷我们在讨论晶体结构时，是将晶体看成无限大，并且构成晶体的每个粒子（原子、分子或离子）都是在自己应有的位置上，这样的理想结构中，每个结点上都有相应的粒子，没有空着的结点，也没有多余的粒子，非常规则地呈周期性排列。

实际晶体是这样的吗？测试表明，与理想晶体相比，实际晶体中会有正常位置空着或空隙位置填进一个额外质点，或杂质进入晶体结构中等等不正常情况，热力学计算表明，这些结构中对理想晶体偏离的晶体才是稳定的，而理想晶体实际上是不存在的。

结构上对理想晶体的偏移被称为晶体缺陷。

实际晶体或多或少地存在着缺陷，这些缺陷的存在自然会对晶体的性质产生或大或小的影响。

晶体缺陷不仅会影响晶体的物理和化学性质，而且还会影响发生在晶体中的过程，如扩散、烧结、化学反应性等。

因而掌握晶体缺陷的知识是掌握材料科学的基础。

晶体的结构缺陷主要类型如表2—1所示。

这些缺陷类型，在无机非金属材料中最基本和最重要的是点缺陷，也是本章的重点。

表2—1 晶体结构缺陷的主要类型2.1 点缺陷研究晶体的缺陷，就是要讨论缺陷的产生、缺陷类型、浓度大小及对各种性质的影响。

60年代，F ．A ．Kroger 和H ．J ．Vink 建立了比较完整的缺陷研究理论——缺陷化学理论，主要用于研究晶体内的点缺陷。

点缺陷是一种热力学可逆缺陷，即它在晶体中的浓度是热力学参数（温度、压力等）的函数，因此可以用化学热力学的方法来研究晶体中点缺陷的平衡问题，这就是缺陷化学的理论基础。

点缺陷理论的适用范围有一定限度，当缺陷浓度超过某一临界值(大约在0．1原子％左右)时，由于缺陷的相互作用，会导致广泛缺陷（缺陷簇等）的生成，甚至会形成超结构和分离的中间相。

但大多数情况下，对许多无机晶体，即使在高温下点缺陷的浓度也不会超过上述极限。

缺陷化学的基本假设：将晶体看作稀溶液，将缺陷看成溶质，用热力学的方法研究各种缺陷在一定条件下的平衡。

也就是将缺陷看作是一种化学物质，它们可以参与化学反应——准化学反应，一定条件下，这种反应达到平衡状态。

晶体结构缺陷

缺陷种类名称点缺陷瞬变缺陷声子电子缺陷电子、空穴原子缺陷空位填隙原子取代原子缔合中心广泛缺陷缺陷簇切变结构块结构线缺陷位错面缺陷晶体表面晶粒晶界体缺陷孔洞和包裹物第二章晶体结构缺陷我们在讨论晶体结构时，是将晶体看成无限大，并且构成晶体的每个粒子（原子、分子或离子）都是在自己应有的位置上，这样的理想结构中，每个结点上都有相应的粒子，没有空着的结点，也没有多余的粒子，非常规则地呈周期性排列。

实际晶体是这样的吗？测试表明，与理想晶体相比，实际晶体中会有正常位置空着或空隙位置填进一个额外质点，或杂质进入晶体结构中等等不正常情况，热力学计算表明，这些结构中对理想晶体偏离的晶体才是稳定的，而理想晶体实际上是不存在的。

结构上对理想晶体的偏移被称为晶体缺陷。

实际晶体或多或少地存在着缺陷，这些缺陷的存在自然会对晶体的性质产生或大或小的影响。

晶体缺陷不仅会影响晶体的物理和化学性质，而且还会影响发生在晶体中的过程，如扩散、烧结、化学反应性等。

因而掌握晶体缺陷的知识是掌握材料科学的基础。

晶体的结构缺陷主要类型如表2—1所示。

这些缺陷类型，在无机非金属材料中最基本和最重要的是点缺陷，也是本章的重点。

表2—1 晶体结构缺陷的主要类型2.1点缺陷研究晶体的缺陷，就是要讨论缺陷的产生、缺陷类型、浓度大小及对各种性质的影响。

60年代，F．A．Kroger和H．J．Vink建立了比较完整的缺陷研究理论——缺陷化学理论，主要用于研究晶体内的点缺陷。

点缺陷是一种热力学可逆缺陷，即它在晶体中的浓度是热力学参数（温度、压力等）的函数，因此可以用化学热力学的方法来研究晶体中点缺陷的平衡问题，这就是缺陷化学的理论基础。

点缺陷理论的适用范围有一定限度，当缺陷浓度超过某一临界值(大约在0．1原子％左右)时，由于缺陷的相互作用，会导致广泛缺陷（缺陷簇等）的生成，甚至会形成超结构和分离的中间相。

但大多数情况下，对许多无机晶体，即使在高温下点缺陷的浓度也不会超过上述极限。

第二章 晶体结构与晶体中的缺陷


• MgO具有NaCl结构，根据O2-半径0.140nm和Mg2+半径为 0.072nm，计算① 球状离子所占据的空间分数（堆积系数） ；② MgO的密度。 • 解：① MgO属于NaCl型结构，即面心立方结构，每个晶胞 中含有4个Mg2+和4个O2-，故MgO所占体积为 • VMgO=4×4/3π (RMg2+3+RO2-3） • =16/3π ×(0.0723+0.1403) • =0.0522（nm3) • ∵Mg2+和O2-在面心立方的棱边上接触 • ∴a=2（RMg2++RO2-）=2×(0.072+0.140)=0.424nm • ∴堆积系数=VMgO/V晶胞=0.0522/(0.424)3=68.5% • ②DMgO=mMgO/V晶胞=n.(M/N0)/a3 • =4×(24.3+16.0)/[(0.424×10-7)3×6.02×1023] • =3.51g/cm3
• ⑷ 蒙脱石结构
• 单元层间：范德华力，弱。 • [SiO4]4-中的Si4+被Al3+取代（ 同晶取代）为平衡电价，吸 附低价正离子，易解吸，使 颗粒荷电，因此使陶瓷制品 因带某些离子具有放射性。 • 性质： • 加水体积膨胀，泥料可塑性 好。
蒙脱石结构 三层型[Al(O4OH2)]7-
• • • • • •
一、NaCl (石盐，Rocksalt) 型结构
Cl-离子做面心立方紧密堆积，而Na+离子是充填在Cl-离子填 充所有八面体空隙之内，按照鲍林第一规则，正负离子半径 比rc/ra应该在0.414-0.732之间。由于面心立方密堆积结构 中，八面体空隙与原子之比是1：1，因此该结构的化合物具 有理想的化学计量比MX。 许多AB型的化合物，包括许多
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（a）与螺位错垂直的 晶面的形状
（b）螺位错滑移面两侧晶面 上原子的滑移情况
图
2-13
螺型位错示意图
（三）混合位错
在外力作用下，两部分之间发生相对滑移， 在晶体内部已滑移和未滑移部分的交线既不垂直 也不平行滑移方向（伯氏矢量b），这样的位错 称为混合位错。如图2-14所示。
位错线上任意一点，经矢量分解后，可分解 为刃位错和螺位错分量。晶体中位错线的形状可 以是任意的，但位错线上各点的伯氏矢量相同， 只是各点的刃型、螺型分量不同而已。
按照完整晶体滑移模型，使晶体滑移所需的临界切应力， 即使整个滑移面的原子从一个平衡位置移动到另一个平衡位 置时，克服能垒所需要的切应力，晶面间的滑移是滑移面上 所有原子整体协同移动的结果，这样可以把晶体的相对滑移 简化为两排原子间的滑移，晶体的理论切变强度m为： Gx/a=msin（2x/）=m2x/ 当x很小时，于是，
位错核心能 弹性应变能
（1）位错核心能Wcore ，在位错核心几个原子间距 r0 =2|b|=2b以内的区域，滑移面两侧原子间的错排能即相 当于位错核心能。错排能约占位错能的1/10，可忽略。 （2）弹性应变能Wel ，在位错核心区以外，长程应力场作 用范围所具有的能量，约占位错能的9/10。
总之：
图2-6 外力作用下晶体滑移示意图（微观）
滑移的可能性（滑移系统）：
在最密排晶面（称为滑移面）的最密排晶向（称为滑移方向）上进行。
晶体滑移的临界分切应力（c） ： 开动晶体滑移系统所需的最小分切应力。
（a）变形前
（b）变形后
图2-7 单晶试棒在拉伸应力作用下的变化（宏观）
(a)孪生面、孪生方向的方位
围绕一个螺位错的晶体圆柱体区域也有应力场存在,只有切应力分量， 切应力分量是轴对称的，正应力分量全为0，螺位错不引起晶体的膨
胀或收缩。
各应力分量的大小与伯氏矢量的模成正比。
位错的应变能Wtot
位错使其周围点阵畸变，点阵能量增加，点阵所增加的
能量即为位错的应变能。包括两部分： Wtot=Wcore+Wel
同向位错，在不同滑移面，当两者所成角度 〈45度时，压应力重叠，张应力重叠，结果互相 排斥，导致远离；当两者所成角度〉45度时，结 果互相吸引，导致接近。
（一）伯格斯矢量的确定及表示
1.确定伯格斯矢量的步骤
（1）对于给定点的位错，人为规定位错
线
的方向，如图2-15所示。
（ 2）
用右手螺旋定则确定伯格斯回路方向。
（3）按照图2-15所示的规律走回路，最后封
闭回路的矢量即要求的伯氏矢量。 2 .伯氏矢量的表示方法 b=ka[uvw]
图2-15 简单立方结构中，围绕刃位错的伯格斯回路
（a）混合位错的 形成
（b）混合位错分解为刃位错 和螺位错示意图 （c）混合位错线附近原 子滑移透视图
图2-14
三、位错的伯格斯矢量（Burgers vector） 及位错的性质
伯格斯矢量：晶体中有位错存在时，滑移面一侧 质点相对于另一侧质点的相对位移或畸变。 性质：大小表征了位错的单位滑移距离，方向与 滑移方向一致。
五、位错的运动

位错的滑移：指位错在外力作用下，在滑移面 上的运动，结果导致永久形变。

位错的攀移：指在热缺陷的作用下，位错在垂
直滑移方向的运动，结果导致空位或间隙原子 的增值或减少。
（一）位错的滑移
1.位错滑移的机理（图2-16） 位错在滑移时是通过位错线或位错附近的原子 逐个移动很小的距离完成的。
六、位错的反应
由于位错间相互作用力的存在，使得位错之
间有可能发生相互转化或相互作用，此即位错反 应。位错能否发生反应，取决于两个条件： 其一，必须满足伯氏矢量的守恒性； 其二，必须满足能量条件。
在同一滑移面的两个异向位错的相互作用， 相互吸引、反应导致位错消失，变成完整晶体。
两个异向位错，在不同滑移面，上下错开一 个原子间距，反应结果生成一排空位。
图2-17 刃位错攀移示意图
位错的攀移力（使位错发生攀移运动的力）包括：
（1）化学攀移力Fs，是指不平衡空位浓度施加给位错攀移的
驱动力。 （2）弹性攀移力Fc，是指作用于半原子面上的正应力分量作 用下，刃位错所受的力。 位错攀移的激活能Uc由割阶形成的激活能Uj及空位的扩 散活化能Ud两部分所组成。常温下位错靠热激活来攀移是 很困难的。但是，在许多高温过程如蠕变、回复、单晶拉 制中，攀移却起着重要作用。位错攀移在低温下是难以进 行的，只有在高温下才可能发生。
（一）完整晶体的塑性变形方式
1.晶体在外力作用下的滑移（图２－６） 滑移的定义：在外力作用下，一部分相对另一部分（晶面、晶向）的平移。 滑移的结果：塑性变形，表面形成台阶
滑移的可能性（滑移系统）：在最密排晶面（称为滑移面）的最密排
晶向（称为滑移方向）上进行。 晶体滑移的临界分切应力（c） ：开动晶体滑移系统所需的最小分切应力。
形成及定义（图2-11） ： 晶体在大于屈服值的切应力作用下，以ABCD面为滑移面 发生滑移。EF是晶体已滑移部分和未滑移部分的交线， 犹如砍入晶体的一把刀的刀刃，即刃位错（或棱位错）。 几何特征：位错线与原子滑移方向相垂直；滑移面上部位错 线周围原子受压应力作用，原子间距小于正常晶格间距； 滑移面下部位错线周围原子受张应力作用，原子间距大于 正常晶格间距。 分类：正刃位错， “” ；负刃位错， “T” 。符号中水平 线代表滑移面，垂直线代表半个原子面。
m=G/（2a）
对于简单立方晶体，a=，则
m=G/（2）
滑移机理
所施加的力必须足以使原子间的键断裂，才 能产生滑移压力大小约为 E/15
F
二、位错的类型
晶体在不同的应力状态下，其滑移方式不同。
根据原子的滑移方向和位错线取向的几何特征 不同，位错分为刃位错、螺位错和混合位错。
（一）刃位错
位错的来源与增殖

一、晶体的塑性和强度


二、位错的类型
三、位错的伯格斯矢量（Burgers vector） 及位错的性质 四、位错的应力场与应变能 五、位错的运动 六、位错的反应

一、晶体的塑性和强度
（一）完整晶体的塑性变形方式 1.晶体在外力作用下的滑移
2.晶体在外力作用下的孪生
（二）完整晶体的理论切变强度
2.晶体在外力作用下的孪生
在外力作用下，晶体的一部分相对于另一部分，沿着一 定的晶面和晶向发生切变，切变之后，两部分晶体的位向
以切变面为镜面呈对称关系。
1.晶体在外力作用下的滑移（图２－６）
滑移的定义：在外力作用 下，一部分相对另一部分 （晶面、晶向）的平移。
τ τ
滑移的结果：塑性变 形，表面形成台阶。
（a）正刃位错滑移方向与 外力方向相图
（b）负刃位错滑移方 向与外力方向相反
图2-16 刃位错的滑移
位错运动示意 τ
τ
刃位错的运动
螺位错的运动
混合位错的运动
2.位错的滑移特点
（ 1 ）刃位错滑移方向与外力 及伯氏矢量 b 平行，正、负 刃位错滑移方向相反。
（ 2 ）螺位错滑移方向与外力 及伯氏矢量 b 垂直，左、右 螺型位错滑移方向相反，理论上包含位错线的任何平面 都是滑移面，实际上还受到晶体学条件的限制。 （ 3 ）混合位错滑移方向与外力 及伯氏矢量 b 成一定角度 （即沿位错线法线方向滑移）。 （4）晶体的滑移方向与外力及位错的伯氏矢量b相一致， 但并不一定与位错的滑移方向相同。
(b)（ 1 1 0 ）晶面：孪生过程中（111） 晶面的移动情况

2.晶体在外力作用下的孪生 在外力作用下，晶体的一部分相对于另一部分，沿着一定的晶面 图2-8 面心立方晶体（111）[11 2] 孪生示意图 和晶向发生切变，切变之后，两部分晶体的位向以切变面为镜面呈 对称关系。
（二）完整晶体的理论切变强度
（二）伯氏矢量的守恒性
对一条位错线而言，其伯氏矢量是固定不
变的，此即位错的伯氏矢量的守恒性。
推论：
1.一条位错线只有一个伯氏矢量。
2.如果几条位错线在晶体内部相交（交点称为节
点），则指向节点的各位错的伯氏矢量之和，必
然等于离开节点的各位错的伯氏矢量之和 。
（三）位错线的连续性及位错密度
1.位错线的连续性 位错线不可能中断于晶体内部。在晶体内部，位错 线要么自成环状回路，要么与其它位错相交于节点，要 么穿过晶体终止于晶界或晶体表面。 2.位错密度：单位体积内位错线的总长度ρ=L/V
图2-11 刃位错示意图
刃型位错示意图：(a)立体模型;(b)平面图
G
H
F
E
晶体局部滑移造成的刃型位错
（二）螺位错
形成及定义（图2-12） ：
晶体在外加剪应力作用下，沿ABCD面滑移，图中 EF线为已滑移区与未滑移区的分界处。由于位错线周围 的一组原子面形成了一个连续的螺旋形坡面，故称为螺 位错。
n l n S l S
式中 L为晶体长度，n为位错线数目，S晶体截面积。 一般退火金属晶体中为104~108cm-2数量级，经剧烈 冷加工的金属晶体中，为1012~1014cm-2.
四、位错的应力场与应变能
理论基础：连续弹性介质模型(固体弹性理论) 假设：1.完全服从虎克定律，即不存在塑性变形；
2.3 线缺陷 （line defects ，dislocation ）
位错模型的提出
背景
完整晶体塑性变形─滑移的模型→金属晶体的理论强度
→理论强度比实测强度高出几个数量级→ 晶体缺陷的设想─ 线缺陷（位错）的模型→ 以位错滑移模型计算出的晶体强度， 与实测值基本相符。
应用
晶体的屈服强度、加工硬化、合金强化、相变强化、脆性断裂、蠕变
2. 各向同性；
3. 连续介质，不存在结构间隙。 方法：建立力学模型（见书上p116、p117） 根据固体弹性理论，建立平衡方程、虎克定律、应变 和位移关系三个方程